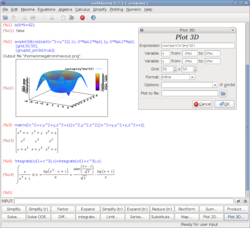
Maxima (software)
Maxima je svobodný počítačový algebraický systém, napsaný v Lispu (resp. jeho dialektu Common Lisp) a distribuovaný pod GNU General Public License. Je dostupný pro všechny platformy standardu POSIX, jakými jsou Unix, BSD nebo Linux; dostupné jsou také binární soubory pro MS Windows. wxMaxima je multiplatformní verzí s grafickým uživatelským rozhraním, založenou na wxWidgets. Maxima vychází z projektu Macsyma, jenž byl vyvíjen v MIT (Massachusetts Institute of Technology) a financován United States Department of Energy a dalšími vládními organizacemi. O vývoj jedné z verzí Macsyma se staral od roku 1982 až do své smrti v roce 2001 Bill Schelter, jenž v roce 1998 získal svolení uveřejnit svou verzi pod GPL. Tuto verzi, nyní nazývanou Maxima, nyní udržuje nezávislá komunita vývojářů a uživatelů. Jako interaktivního grafického rozhraní pro Maximu lze využít programu GNU TeXmacs. Dalšími možnostmi jsou front end imaxima nebo interaktivní mód editoru Emacs. Ovládání MaximyPři spuštění vypíše Maxima Hlášení o distribuci pod GNU General Public License a pak už rovnou výzvu k zadání příkazu. Od verze 5.9.1 včetně je to (%i1), dříve (C1). Výzvu však můžeme jednoduše změnit nastavením proměnných inchar a outchar. Základní pravidla pro psaní příkazů:
Základní aritmetické operaceMaxima se dá používat jako jednoduchá kalkulačka. Pokud počítáme celočíselně, stačí zadat např.: (C1) 1+1; a výstupem nám bude (D1) 2 Podobně i jiné operace: (C2) 9-6/3; (D2) 7 (C3) 5^3-5*5; (D3) 100 (C4) 5!+4!; (D4) 144 Pokud zadáme k výpočet s neceločíselným výsledkem, Maxima ho převede na zlomek v základním tvaru. (C5) 18/4;
9
(D5) -
2
Jestliže chceme dostat výsledek ve tvaru desetinného čísla, musíme zapsat za výpočet parametr numer. (C6) 18/4,numer; (D6) 4.5 Úprava výrazůPokud zadáme algebraický výraz, nejdříve se jenom opíše, např.: (C7) (x+5)^3;
3
(D7) (x + 5)
Pokud chceme výraz roznásobit (udělat z něj polynom), použijeme příkaz expand(výraz);. Pokud roznásobujeme nebo jinak používáme poslední příkaz, stačí místo něho napsat procento %. Pokud odkazujeme na jiný, dříve použitý příkaz, použijeme jeho název, např. C1, či D5. (C8) expand(%);
3 2
(D8) x + 15x + 75x + 125
Jiná je situace u lomeného výrazu, u kterého nám expand(); nepomůže. Pro zkrácení použijeme příkaz radcan(výraz); (C9) (a^2-b^2)/(a+b);
2 2
a - b
(D9) -------
a + b
(C10) expand(%);
2 2
a b
(D10) ----- + -----
a + b a + b
(C11) radcan(%);
(D11) a - b
Ludolfovo a Eulerovo číslo, výpočty s velkou přesnostíMaxima zná Ludolfovo číslo π, které označuje %pi a Eulerovo číslo e, které označuje %e a umí je normálním způsobem používat ve výrazech a rovnicích. Pokud nezadáme parametr numer, počítá výsledky rovněž s těmito čísly. (C12) 2*3/%pi;
6
(D12) ---
%pi
(C13) %, numer;
(D13) 1.909859317102744
Parametr numer počítá s přesností na 16 platných číslic. Ten samý výsledek v semilogaritmickém tvaru dostaneme použitím funkce bfloat(výraz);. Ten má primární přesnost také 16 platných číslic. Tu však můžeme měnit pomocí proměnné fpprec. Nejdříve si pomocí zadání fpprec; ověříme, že přesnost je skutečně 16 a pak ji změníme na 121: (C14) bfloat(%e);
(D14) 2.718281828459045B0
(C15) fpprec;
(D15) 16
(C16) fpprec: 121;
(D16) 121
(C17) bfloat(%e);
(D17) 2.718281828459045235360287471352662497757247093699959574966967627724076#
630353547594571382178525166427427466391932003059922B0
B0 zde vlastně znamená „krát deset na nultou“. Pokud použijeme funkci bfloat(); ve výrazu, pak se celý počítá s přesností fpprec. Řešení lineárních rovnicK řešení jedná rovnice slouží funkce solve(rovnice,neznámé);. K řešení soustavy lineárních rovnic slouží funkce linsolve([rovnice],[neznámá]);. (C18) a:x+y=5; (D18) y + x = 5 (C19) b:x-y=1; (D19) x - y = 1 (C20) linsolve([a,b],[x,y]); (D20) [x = 3, y = 2] Související článkyExterní odkazy
|
||||||||||||||||||
Portal di Ensiklopedia Dunia