V├ĪlecV├Īlec je v prostorov├® geometrii t─øleso, vymezen├® dv─øma rovnob─ø┼Šn├Įmi podstavami a pl├Ī┼Īt─øm. Pl├Ī┼Ī┼ź je rozvinuteln├Ī plocha, v┼Īechny povrchov├® (tvo┼Ö├Łc├Ł) p┼Ö├Łmky pl├Ī┼Īt─ø jsou rovnob─ø┼Šn├® a pokud jsou k podstav├Īm kolm├®, hovo┼Ö├Łme o kolm├®m v├Īlci. V opa─Źn├®m p┼Ö├Łpad─ø se jedn├Ī o v├Īlec kos├Į. Vzd├Īlenost mezi podstavami se naz├Įv├Ī v├Į┼Īka v├Īlce. Vzd├Īlenost mezi dv─øma podstavami pod├®l pl├Ī┼Īt─ø (tj. pod├®l povrchov├® p┼Ö├Łmky) se naz├Įv├Ī strana v├Īlce. Je-li podstavou kruh, pak v├Īlec ozna─Ź├Łme jako kruhov├Į. Kolm├Į kruhov├Į v├Īlec naz├Įv├Īme rota─Źn├Łm v├Īlcem. P┼Ö├Łmku proch├Īzej├Łc├Ł st┼Öedy obou podstav rota─Źn├Łho v├Īlce naz├Įv├Īme osou rotace. 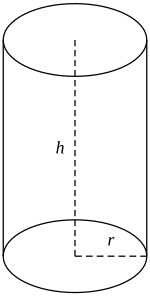 Rota─Źn├Ł v├ĪlecNej─Źast─øji se v├Īlcem rozum├Ł rota─Źn├Ł v├Īlec, kolm├Į v├Īlec, jeho┼Š podstavou je kruh. M├Ī tak├® ┼Öadu r┼»zn├Įch aplikac├Ł. Vlastnosti
kde je polom─ør podstavy a je v├Į┼Īka v├Īlce.
Pro obsah cel├®ho povrchu rota─Źn├Łho v├Īlce pak plat├Ł
V├Īlcov├Ī plocha a prostor Jednoduchou p┼Öedstavu rota─Źn├Łho v├Īlce lze roz┼Ī├Ł┼Öit a zobecnit. M─øjme jednoduchou uzav┼Öenou k┼Öivku , kter├Ī le┼Š├Ł v rovin─ø. Body, kter├® le┼Š├Ł na vz├Ījemn─ø rovnob─ø┼Šn├Įch p┼Ö├Łmk├Īch proch├Īzej├Łc├Łch libovoln├Įm bodem k┼Öivky , tvo┼Ö├Ł v├Īlcovou plochu. ─ī├Īst prostoru ohrani─Źen├Ī v├Īlcovou plochou se naz├Įv├Ī v├Īlcov├Į prostor. RovniceV├Īlcov├Ī plocha (kvadratick├Į v├Īlec) b├Įv├Ī ozna─Źov├Īna podle ┼Ö├Łd├Łc├Ł k┼Öivky.  Eliptick├Į kvadratick├Į v├ĪlecEliptick├Į kvadratick├Į v├Īlec lze vyj├Īd┼Öit rovnic├Ł ┼ś├Łd├Łc├Ł k┼Öivkou eliptick├®ho v├Īlce je elipsa le┼Š├Łc├Ł v rovin─ø s rovnic├Ł a tvo┼Ö├Łc├Ł p┼Ö├Łmky v├Īlce jsou rovnob─ø┼Šn├® s osou . Pro se jedn├Ī o rota─Źn├Ł v├Īlec s osou rotace . Hyperbolick├Į kvadratick├Į v├ĪlecHyperbolick├Į kvadratick├Į v├Īlec lze vyj├Īd┼Öit rovnic├Ł ┼ś├Łd├Łc├Ł k┼Öivkou hyperbolick├®ho v├Īlce je hyperbola le┼Š├Łc├Ł v rovin─ø s rovnic├Ł a tvo┼Ö├Łc├Ł p┼Ö├Łmky v├Īlce jsou rovnob─ø┼Šn├® s osou . Parabolick├Į kvadratick├Į v├ĪlecParabolick├Į kvadratick├Į v├Īlec lze vyj├Īd┼Öit rovnic├Ł ┼ś├Łd├Łc├Ł k┼Öivkou parabolick├®ho v├Īlce je parabola le┼Š├Łc├Ł v rovin─ø s rovnic├Ł a tvo┼Ö├Łc├Ł p┼Ö├Łmky v├Īlce jsou rovnob─ø┼Šn├® s osou . Obecn├Į v├ĪlecObecnou v├Īlcovou plochu, jej├Ł┼Š ┼Ö├Łd├Łc├Ł k┼Öivka le┼Š├Ł v rovin─ø a m├Ī rovnici , a jej├Ł tvo┼Ö├Łc├Ł p┼Ö├Łmky jsou rovnob─ø┼Šn├® s osou , lze zapsat rovnic├Ł Obecn─ø lze ┼Ö├Łci, ┼Še pokud v rovnici plochy chyb├Ł jedna z prom─ønn├Įch, pak se jedn├Ī o rovnici v├Īlcov├® plochy, jej├Ł┼Š tvo┼Ö├Łc├Ł p┼Ö├Łmky jsou rovnob─ø┼Šn├® s osou, kter├Ī odpov├Łd├Ī chyb─øj├Łc├Ł prom─ønn├®, a jej├Ł┼Š ┼Ö├Łd├Łc├Ł k┼Öivka m├Ī stejnou rovnici jako dan├Ī plocha a le┼Š├Ł v rovin─ø kolm├® k tvo┼Ö├Łc├Łm p┼Ö├Łmk├Īm. Jsou-li tvo┼Ö├Łc├Ł p┼Ö├Łmky rovnob─ø┼Šn├® s vektorem , pak lze rovnici v├Īlcov├® plochy p┼Öev├®st na tvar VlastnostiObjem v├Īlce ur─Ź├Łme ze vztahu
kde je obsah podstavy a je hloubka v├Īlce. Obsah povrchu v├Īlce je d├Īn vztahem
kde je obsah podstavy a je obsah pl├Ī┼Īt─ø v├Īlce. OdkazyLiteratura
Souvisej├Łc├Ł ─Źl├ĪnkyExtern├Ł odkazy
|
Portal di Ensiklopedia Dunia

































