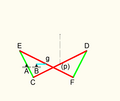
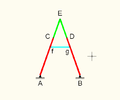
Hart's inversors Link dimensions: Crank and fixed: a Rocker: b (anchored at midpoint) Coupler: c (joint at midpoint) Hart's inversors are two planar mechanisms that provide a perfect straight line motion using only rotary joints.[1] They were invented and published by Harry Hart in 1874–5.[1][2] Hart's first inversorHart's first inversor, also known as Hart's W-frame, is based on an antiparallelogram. The addition of fixed points and a driving arm make it a 6-bar linkage. It can be used to convert rotary motion to a perfect straight line by fixing a point on one short link and driving a point on another link in a circular arc.[1][3] Rectilinear bar and quadruplanar inversors Hart's first inversor is demonstrated as a six-bar linkage with only a single point that travels in a straight line. This can be modified into an eight-bar linkage with a bar that travels in a rectilinear fashion, by taking the ground and input (shown as cyan in the animation), and appending it onto the original output. A further generalization by James Joseph Sylvester and Alfred Kempe extends this such that the bars can instead be pairs of plates with similar dimensions. Hart's second inversor Link dimensions:[Note 1] Double rocker: 3a + a (distance between anchors: 2b) Coupler: b Tip of the A: 2a Hart's second inversor, also known as Hart's A-frame, is less flexible in its dimensions,[Note 1] but has the useful property that the motion perpendicularly bisects the fixed base points. It is shaped like a capital A – a stacked trapezium and triangle. It is also a 6-bar linkage. Geometric construction of the A-frame inversorExample dimensionsThese are the example dimensions that you see in the animations on the right.
See also
Notes
References
External linksWikimedia Commons has media related to Hart's inversor.
|
Portal di Ensiklopedia Dunia
![{\displaystyle {\begin{aligned}b&<c\\[4pt]2a&<{\tfrac {1}{2}}b+{\tfrac {1}{2}}c\\[2pt]{\tfrac {1}{2}}c&<{\tfrac {1}{2}}b+2a\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13d497f57a6f1006bd13a5acb4a7773e86490c7c)