Hexagonal tiling honeycomb
Hexagonal tiling honeycomb
Perspective projection viewPoincaré disk model
Type
Hyperbolic regular honeycomb Paracompact uniform honeycomb
Schläfli symbols {6,3,3}[3] }[3,3] }
Coxeter diagrams
Cells
{6,3}
Faces
hexagon {6}
Edge figure triangle {3}
Vertex figure tetrahedron {3,3}
Dual Order-6 tetrahedral honeycomb
Coxeter groups
V
¯
3
{\displaystyle {\overline {V}}_{3}}
Y
¯
3
{\displaystyle {\overline {Y}}_{3}}
Z
¯
3
{\displaystyle {\overline {Z}}_{3}}
V
P
¯
3
{\displaystyle {\overline {VP}}_{3}}
[3] ]
P
P
¯
3
{\displaystyle {\overline {PP}}_{3}}
[3,3] ]
Properties
Regular
In the field of hyperbolic geometry , the hexagonal tiling honeycomb is one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space . It is paracompact because it has cells composed of an infinite number of faces. Each cell is a hexagonal tiling whose vertices lie on a horosphere , a surface in hyperbolic space that approaches a single ideal point at infinity.
The Schläfli symbol of the hexagonal tiling honeycomb is {6,3,3}. Since that of the hexagonal tiling is {6,3}, this honeycomb has three such hexagonal tilings meeting at each edge. Since the Schläfli symbol of the tetrahedron is {3,3}, the vertex figure of this honeycomb is a tetrahedron. Thus, four hexagonal tilings meet at each vertex of this honeycomb, six hexagons meet at each vertex, and four edges meet at each vertex.[ 1]
Images
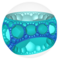
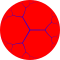
Viewed in perspective outside of a Poincaré disk model , the image above shows one hexagonal tiling cell within the honeycomb, and its mid-radius horosphere (the horosphere incident with edge midpoints). In this projection, the hexagons grow infinitely small towards the infinite boundary, asymptoting towards a single ideal point. It can be seen as similar to the order-3 apeirogonal tiling , {∞,3} of H2 , with horocycles circumscribing vertices of apeirogonal faces.
{6,3,3}
{∞,3}
One hexagonal tiling cell of the hexagonal tiling honeycomb
An order-3 apeirogonal tiling with a green apeirogon and its horocycle
Symmetry constructions
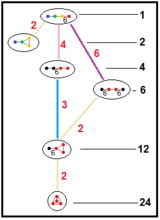
Subgroup relations It has a total of five reflectional constructions from five related Coxeter groups all with four mirrors and only the first being regular: [3] ] and [3[3,3] ] larger fundamental domains respectively . In Coxeter notation subgroup markups, they are related as: [6,(3,3)* ] (remove 3 mirrors, index 24 subgroup); [3,6,3* ] or [3* ,6,3] (remove 2 mirrors, index 6 subgroup); [1+ ,6,3,6,1+ ] (remove two orthogonal mirrors, index 4 subgroup); all of these are isomorphic to [3[3,3] ]. The ringed Coxeter diagrams are Wythoff construction .
The hexagonal tiling honeycomb is a regular hyperbolic honeycomb in 3-space, and one of 11 which are paracompact.
11 paracompact regular honeycombs
{6,3,3}
{6,3,4}
{6,3,5}
{6,3,6}
{4,4,3}
{4,4,4}
{3,3,6}
{4,3,6}
{5,3,6}
{3,6,3}
{3,4,4}
It is one of 15 uniform paracompact honeycombs in the [6,3,3] Coxeter group, along with its dual, the order-6 tetrahedral honeycomb .
[6,3,3] family honeycombs
{6,3,3}
r{6,3,3}
t{6,3,3}
rr{6,3,3}
t0,3 {6,3,3}
tr{6,3,3}
t0,1,3 {6,3,3}
t0,1,2,3 {6,3,3}
{3,3,6}
r{3,3,6}
t{3,3,6}
rr{3,3,6}
2t{3,3,6}
tr{3,3,6}
t0,1,3 {3,3,6}
t0,1,2,3 {3,3,6}
It is part of a sequence of regular polychora , which include the 5-cell {3,3,3}, tesseract {4,3,3}, and 120-cell {5,3,3} of Euclidean 4-space, along with other hyperbolic honeycombs containing tetrahedral vertex figures .
{p,3,3} honeycombs
Space
S3
H3
Form
Finite
Paracompact
Noncompact
Name
{3,3,3}
{4,3,3}
{5,3,3}
{6,3,3}
{7,3,3}
{8,3,3}
... {∞,3,3}
Image
Coxeter diagrams 1
4
6
12
24
Cells
{3,3} {4,3} {5,3} {6,3} {7,3} {8,3} {∞,3}
It is also part of a sequence of regular honeycombs of the form {6,3,p}, which are each composed of hexagonal tiling cells:
{6,3,p } honeycombs
Space
H3
Form
Paracompact
Noncompact
Name
{6,3,3}
{6,3,4}
{6,3,5}
{6,3,6}
{6,3,7}
{6,3,8}
... {6,3,∞}
Coxeter
Image
Vertex
{3,3} {3,4} {3,5} {3,6} {3,7} {3,8} {3,∞}
Rectified hexagonal tiling honeycomb
Rectified hexagonal tiling honeycomb
Type
Paracompact uniform honeycomb
Schläfli symbols r{6,3,3} or t1 {6,3,3}
Coxeter diagrams
Cells
{3,3} r{6,3}
Faces
triangle {3}hexagon {6}
Vertex figure triangular prism
Coxeter groups
V
¯
3
{\displaystyle {\overline {V}}_{3}}
P
¯
3
{\displaystyle {\overline {P}}_{3}}
[3] ]
Properties
Vertex-transitive, edge-transitive
The rectified hexagonal tiling honeycomb , t1 {6,3,3}, tetrahedral and trihexagonal tiling facets, with a triangular prism vertex figure . The
Hexagonal tiling honeycomb
Rectified hexagonal tiling honeycomb
Related H2 tilings
Order-3 apeirogonal tiling
Triapeirogonal tiling
Truncated hexagonal tiling honeycomb
Truncated hexagonal tiling honeycomb
Type
Paracompact uniform honeycomb
Schläfli symbol t{6,3,3} or t0,1 {6,3,3}
Coxeter diagram
Cells
{3,3} t{6,3}
Faces
triangle {3}dodecagon {12}
Vertex figure triangular pyramid
Coxeter groups
V
¯
3
{\displaystyle {\overline {V}}_{3}}
Properties
Vertex-transitive
The truncated hexagonal tiling honeycomb , t0,1 {6,3,3}, tetrahedral and truncated hexagonal tiling facets, with a triangular pyramid vertex figure .
It is similar to the 2D hyperbolic truncated order-3 apeirogonal tiling , t{∞,3} with apeirogonal and triangle faces:
Bitruncated hexagonal tiling honeycomb
Bitruncated hexagonal tiling honeycomb
Type
Paracompact uniform honeycomb
Schläfli symbol 2t{6,3,3} or t1,2 {6,3,3}
Coxeter diagram
Cells
t{3,3} t{3,6}
Faces
triangle {3}hexagon {6}
Vertex figure digonal disphenoid
Coxeter groups
V
¯
3
{\displaystyle {\overline {V}}_{3}}
P
¯
3
{\displaystyle {\overline {P}}_{3}}
[3] ]
Properties
Vertex-transitive
The bitruncated hexagonal tiling honeycomb or bitruncated order-6 tetrahedral honeycomb , t1,2 {6,3,3}, truncated tetrahedron and hexagonal tiling cells, with a digonal disphenoid vertex figure .
Cantellated hexagonal tiling honeycomb
Cantellated hexagonal tiling honeycomb
Type
Paracompact uniform honeycomb
Schläfli symbol rr{6,3,3} or t0,2 {6,3,3}
Coxeter diagram
Cells
r{3,3} rr{6,3} {}×{3}
Faces
triangle {3}square {4}hexagon {6}
Vertex figure wedge
Coxeter groups
V
¯
3
{\displaystyle {\overline {V}}_{3}}
Properties
Vertex-transitive
The cantellated hexagonal tiling honeycomb , t0,2 {6,3,3}, octahedron , rhombitrihexagonal tiling , and triangular prism cells, with a wedge vertex figure .
Cantitruncated hexagonal tiling honeycomb
Cantitruncated hexagonal tiling honeycomb
Type
Paracompact uniform honeycomb
Schläfli symbol tr{6,3,3} or t0,1,2 {6,3,3}
Coxeter diagram
Cells
t{3,3} tr{6,3} {}×{3}
Faces
triangle {3}square {4}hexagon {6}dodecagon {12}
Vertex figure mirrored sphenoid
Coxeter groups
V
¯
3
{\displaystyle {\overline {V}}_{3}}
Properties
Vertex-transitive
The cantitruncated hexagonal tiling honeycomb , t0,1,2 {6,3,3}, truncated tetrahedron , truncated trihexagonal tiling , and triangular prism cells, with a mirrored sphenoid vertex figure .
Runcinated hexagonal tiling honeycomb
The runcinated hexagonal tiling honeycomb , t0,3 {6,3,3}, tetrahedron , hexagonal tiling , hexagonal prism , and triangular prism cells, with an irregular triangular antiprism vertex figure .
Runcitruncated hexagonal tiling honeycomb
The runcitruncated hexagonal tiling honeycomb , t0,1,3 {6,3,3}, cuboctahedron , triangular prism , dodecagonal prism , and truncated hexagonal tiling cells, with an isosceles-trapezoidal pyramid vertex figure .
Runcicantellated hexagonal tiling honeycomb
The runcicantellated hexagonal tiling honeycomb or runcitruncated order-6 tetrahedral honeycomb , t0,2,3 {6,3,3}, truncated tetrahedron , hexagonal prism , and rhombitrihexagonal tiling cells, with an isosceles-trapezoidal pyramid vertex figure .
Omnitruncated hexagonal tiling honeycomb
Omnitruncated hexagonal tiling honeycomb
Type
Paracompact uniform honeycomb
Schläfli symbol t0,1,2,3 {6,3,3}
Coxeter diagram
Cells
tr{3,3} {}x{6} {}x{12} tr{6,3}
Faces
square {4}hexagon {6}dodecagon {12}
Vertex figure tetrahedron
Coxeter groups
V
¯
3
{\displaystyle {\overline {V}}_{3}}
Properties
Vertex-transitive
The omnitruncated hexagonal tiling honeycomb or omnitruncated order-6 tetrahedral honeycomb , t0,1,2,3 {6,3,3}, truncated octahedron , hexagonal prism , dodecagonal prism , and truncated trihexagonal tiling cells, with an irregular tetrahedron vertex figure .
See also
References
^ Coxeter The Beauty of Geometry , 1999, Chapter 10, Table III
Coxeter , Regular Polytopes ISBN 0-486-61480-8 The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678 , ISBN 0-486-40919-8 Regular Honeycombs in Hyperbolic Space Archived 2016-06-10 at the Wayback Machine ) Table IIIJeffrey R. Weeks The Shape of Space, 2nd edition ISBN 0-8247-0709-5 N. W. Johnson, R. Kellerhals , J. G. Ratcliffe, S. T. Tschantz, The size of a hyperbolic Coxeter simplex , Transformation Groups (1999), Volume 4, Issue 4, pp 329–353 [1] [2]
N. W. Johnson, R. Kellerhals , J. G. Ratcliffe, S. T. Tschantz, Commensurability classes of hyperbolic Coxeter groups , (2002) H3 : p130. [3]
External links