Kaniadakis exponential distribution

The Kaniadakis exponential distribution (or κ-exponential distribution) is a probability distribution arising from the maximization of the Kaniadakis entropy under appropriate constraints. It is one example of a Kaniadakis distribution. The κ-exponential is a generalization of the exponential distribution in the same way that Kaniadakis entropy is a generalization of standard Boltzmann–Gibbs entropy or Shannon entropy.^[1] The κ-exponential distribution of Type I is a particular case of the κ-Gamma distribution, whilst the κ-exponential distribution of Type II is a particular case of the κ-Weibull distribution.

κ-exponential distribution of type I

Probability density function
Cumulative distribution function
Parameters	${\displaystyle 0<\kappa <1}$ shape (real) ${\displaystyle \beta >0}$ rate (real)
Support	${\displaystyle x\in [0,\infty )}$
PDF	${\displaystyle (1-\kappa ^{2})\beta \exp _{\kappa }(-\beta x)}$
CDF	${\displaystyle 1-{\Big (}{\sqrt {1+\kappa ^{2}\beta ^{2}x^{2}}}+\kappa ^{2}\beta x{\Big )}\exp _{k}({-\beta x)}}$
Mean	${\displaystyle {\frac {1}{\beta }}{\frac {1-\kappa ^{2}}{1-4\kappa ^{2}}}}$
Variance	${\displaystyle \sigma _{\kappa }^{2}={\frac {1}{\beta ^{2}}}{\frac {2(1-4\kappa ^{2})^{2}-(1-\kappa ^{2})^{2}(1-9\kappa ^{2})}{(1-4\kappa ^{2})^{2}(1-9\kappa ^{2})}}}$
Skewness	${\displaystyle {\frac {2(1-\kappa ^{2})(144\kappa ^{8}+23\kappa ^{6}+27\kappa ^{4}-6\kappa ^{2}+1)}{\beta ^{3}\sigma _{\kappa }^{3}(4\kappa ^{2}-1)^{3}(144\kappa ^{4}-25\kappa ^{2}+1)}}}$
Excess kurtosis	${\displaystyle {\frac {9(1200\kappa ^{14}-6123\kappa ^{12}+562\kappa ^{10}+1539\kappa ^{8}-544\kappa ^{6}+143\kappa ^{4}-18\kappa ^{2}+1)}{\beta ^{4}\sigma _{\kappa }^{4}(1-\kappa ^{2})^{-1}(1-4\kappa ^{2})^{4}(3600\kappa ^{8}-4369\kappa ^{6}+819\kappa ^{4}-51\kappa ^{2}+1)}}-3}$
Method of moments	${\displaystyle {\frac {1-\kappa ^{2}}{\prod _{n=0}^{m+1}[1-(2n-m-1)\kappa ]}}{\frac {m!}{\beta ^{m}}}}$

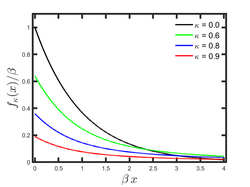
The Kaniadakis κ-exponential distribution of Type I is part of a class of statistical distributions emerging from the Kaniadakis κ-statistics which exhibit power-law tails. This distribution has the following probability density function:^[2]

${\displaystyle f_{_{\kappa }}(x)=(1-\kappa ^{2})\beta \exp _{\kappa }(-\beta x)}$

valid for ${\displaystyle x\geq 0}$, where ${\displaystyle 0\leq |\kappa |<1}$ is the entropic index associated with the Kaniadakis entropy and ${\displaystyle \beta >0}$ is known as rate parameter. The exponential distribution is recovered as ${\displaystyle \kappa \rightarrow 0.}$

The cumulative distribution function of κ-exponential distribution of Type I is given by

${\displaystyle F_{\kappa }(x)=1-{\Big (}{\sqrt {1+\kappa ^{2}\beta ^{2}x^{2}}}+\kappa ^{2}\beta x{\Big )}\exp _{k}({-\beta x)}}$

for ${\displaystyle x\geq 0}$. The cumulative exponential distribution is recovered in the classical limit ${\displaystyle \kappa \rightarrow 0}$.

The κ-exponential distribution of type I has moment of order ${\displaystyle m\in \mathbb {N} }$ given by^[2]

${\displaystyle \operatorname {E} [X^{m}]={\frac {1-\kappa ^{2}}{\prod _{n=0}^{m+1}[1-(2n-m-1)\kappa ]}}{\frac {m!}{\beta ^{m}}}}$

where ${\displaystyle f_{\kappa }(x)}$ is finite if ${\displaystyle 0<m+1<1/\kappa }$.

The expectation is defined as:

${\displaystyle \operatorname {E} [X]={\frac {1}{\beta }}{\frac {1-\kappa ^{2}}{1-4\kappa ^{2}}}}$

and the variance is:

${\displaystyle \operatorname {Var} [X]=\sigma _{\kappa }^{2}={\frac {1}{\beta ^{2}}}{\frac {2(1-4\kappa ^{2})^{2}-(1-\kappa ^{2})^{2}(1-9\kappa ^{2})}{(1-4\kappa ^{2})^{2}(1-9\kappa ^{2})}}}$

The kurtosis of the κ-exponential distribution of type I may be computed thought:

${\displaystyle \operatorname {Kurt} [X]=\operatorname {E} \left[{\frac {\left[X-{\frac {1}{\beta }}{\frac {1-\kappa ^{2}}{1-4\kappa ^{2}}}\right]^{4}}{\sigma _{\kappa }^{4}}}\right]}$

Thus, the kurtosis of the κ-exponential distribution of type I distribution is given by:

${\displaystyle \operatorname {Kurt} [X]={\frac {9(1-\kappa ^{2})(1200\kappa ^{14}-6123\kappa ^{12}+562\kappa ^{10}+1539\kappa ^{8}-544\kappa ^{6}+143\kappa ^{4}-18\kappa ^{2}+1)}{\beta ^{4}\sigma _{\kappa }^{4}(1-4\kappa ^{2})^{4}(3600\kappa ^{8}-4369\kappa ^{6}+819\kappa ^{4}-51\kappa ^{2}+1)}}\quad {\text{for}}\quad 0\leq \kappa <1/5}$

or

${\displaystyle \operatorname {Kurt} [X]={\frac {9(9\kappa ^{2}-1)^{2}(\kappa ^{2}-1)(1200\kappa ^{14}-6123\kappa ^{12}+562\kappa ^{10}+1539\kappa ^{8}-544\kappa ^{6}+143\kappa ^{4}-18\kappa ^{2}+1)}{\beta ^{2}(1-4\kappa ^{2})^{2}(9\kappa ^{6}+13\kappa ^{4}-5\kappa ^{2}+1)(3600\kappa ^{8}-4369\kappa ^{6}+819\kappa ^{4}-51\kappa ^{2}+1)}}\quad {\text{for}}\quad 0\leq \kappa <1/5}$

The kurtosis of the ordinary exponential distribution is recovered in the limit ${\displaystyle \kappa \rightarrow 0}$.

The skewness of the κ-exponential distribution of type I may be computed thought:

${\displaystyle \operatorname {Skew} [X]=\operatorname {E} \left[{\frac {\left[X-{\frac {1}{\beta }}{\frac {1-\kappa ^{2}}{1-4\kappa ^{2}}}\right]^{3}}{\sigma _{\kappa }^{3}}}\right]}$

Thus, the skewness of the κ-exponential distribution of type I distribution is given by:

${\displaystyle \operatorname {Shew} [X]={\frac {2(1-\kappa ^{2})(144\kappa ^{8}+23\kappa ^{6}+27\kappa ^{4}-6\kappa ^{2}+1)}{\beta ^{3}\sigma _{\kappa }^{3}(4\kappa ^{2}-1)^{3}(144\kappa ^{4}-25\kappa ^{2}+1)}}\quad {\text{for}}\quad 0\leq \kappa <1/4}$

The kurtosis of the ordinary exponential distribution is recovered in the limit ${\displaystyle \kappa \rightarrow 0}$.

κ-exponential distribution of type II

Probability density function
Cumulative distribution function
Parameters	${\displaystyle 0\leq \kappa <1}$ shape (real) ${\displaystyle \beta >0}$ rate (real)
Support	${\displaystyle x\in [0,\infty )}$
PDF	${\displaystyle {\frac {\beta }{\sqrt {1+\kappa ^{2}\beta ^{2}x^{2}}}}\exp _{\kappa }(-\beta x)}$
CDF	${\displaystyle 1-\exp _{k}({-\beta x)}}$
Quantile	${\displaystyle \beta ^{-1}\ln _{\kappa }{\Bigg (}{\frac {1}{1-F_{\kappa }}}{\Bigg )},0\leq F_{\kappa }\leq 1}$
Mean	${\displaystyle {\frac {1}{\beta }}{\frac {1}{1-\kappa ^{2}}}}$
Median	${\displaystyle \beta ^{-1}\ln _{\kappa }(2)}$
Mode	${\displaystyle {\frac {1}{\kappa \beta {\sqrt {2(1-\kappa ^{2})}}}}}$
Variance	${\displaystyle \sigma _{\kappa }^{2}={\frac {1}{\beta ^{2}}}{\frac {1+2\kappa ^{4}}{(1-4\kappa ^{2})(1-\kappa ^{2})^{2}}}}$
Skewness	${\displaystyle {\frac {2(15\kappa ^{6}+6\kappa ^{4}+2\kappa ^{2}+1)}{(1-9\kappa ^{2})(2\kappa ^{4}+1)}}{\sqrt {\frac {1-4\kappa ^{2}}{1+2\kappa ^{4}}}}}$
Excess kurtosis	${\displaystyle {\frac {3(72\kappa ^{10}-360\kappa ^{8}-44\kappa ^{6}-32\kappa ^{4}+7\kappa ^{2}-3)}{(4\kappa ^{2}-1)^{-1}(2\kappa ^{4}+1)^{2}(144\kappa ^{4}-25\kappa ^{2}+1)}}}$
Method of moments	${\displaystyle {\frac {\beta ^{-m}m!}{\prod _{n=0}^{m}[1-(2n-m)\kappa ]}}}$

The Kaniadakis κ-exponential distribution of Type II also is part of a class of statistical distributions emerging from the Kaniadakis κ-statistics which exhibit power-law tails, but with different constraints. This distribution is a particular case of the Kaniadakis κ-Weibull distribution with ${\displaystyle \alpha =1}$ is:^[2]

${\displaystyle f_{_{\kappa }}(x)={\frac {\beta }{\sqrt {1+\kappa ^{2}\beta ^{2}x^{2}}}}\exp _{\kappa }(-\beta x)}$

valid for ${\displaystyle x\geq 0}$, where ${\displaystyle 0\leq |\kappa |<1}$ is the entropic index associated with the Kaniadakis entropy and ${\displaystyle \beta >0}$ is known as rate parameter.

The exponential distribution is recovered as ${\displaystyle \kappa \rightarrow 0.}$

The cumulative distribution function of κ-exponential distribution of Type II is given by

${\displaystyle F_{\kappa }(x)=1-\exp _{k}({-\beta x)}}$

for ${\displaystyle x\geq 0}$. The cumulative exponential distribution is recovered in the classical limit ${\displaystyle \kappa \rightarrow 0}$.

The κ-exponential distribution of type II has moment of order ${\displaystyle m<1/\kappa }$ given by^[2]

${\displaystyle \operatorname {E} [X^{m}]={\frac {\beta ^{-m}m!}{\prod _{n=0}^{m}[1-(2n-m)\kappa ]}}}$

The expectation value and the variance are:

${\displaystyle \operatorname {E} [X]={\frac {1}{\beta }}{\frac {1}{1-\kappa ^{2}}}}$

${\displaystyle \operatorname {Var} [X]=\sigma _{\kappa }^{2}={\frac {1}{\beta ^{2}}}{\frac {1+2\kappa ^{4}}{(1-4\kappa ^{2})(1-\kappa ^{2})^{2}}}}$

The mode is given by:

${\displaystyle x_{\textrm {mode}}={\frac {1}{\kappa \beta {\sqrt {2(1-\kappa ^{2})}}}}}$

The kurtosis of the κ-exponential distribution of type II may be computed thought:

${\displaystyle \operatorname {Kurt} [X]=\operatorname {E} \left[\left({\frac {X-{\frac {1}{\beta }}{\frac {1}{1-\kappa ^{2}}}}{\sigma _{\kappa }}}\right)^{4}\right]}$

Thus, the kurtosis of the κ-exponential distribution of type II distribution is given by:

${\displaystyle \operatorname {Kurt} [X]={\frac {3(72\kappa ^{10}-360\kappa ^{8}-44\kappa ^{6}-32\kappa ^{4}+7\kappa ^{2}-3)}{\beta ^{4}\sigma _{\kappa }^{4}(\kappa ^{2}-1)^{4}(576\kappa ^{6}-244\kappa ^{4}+29\kappa ^{2}-1)}}\quad {\text{ for }}\quad 0\leq \kappa <1/4}$

or

${\displaystyle \operatorname {Kurt} [X]={\frac {3(72\kappa ^{10}-360\kappa ^{8}-44\kappa ^{6}-32\kappa ^{4}+7\kappa ^{2}-3)}{(4\kappa ^{2}-1)^{-1}(2\kappa ^{4}+1)^{2}(144\kappa ^{4}-25\kappa ^{2}+1)}}\quad {\text{ for }}\quad 0\leq \kappa <1/4}$

The skewness of the κ-exponential distribution of type II may be computed thought:

${\displaystyle \operatorname {Skew} [X]=\operatorname {E} \left[{\frac {\left[X-{\frac {1}{\beta }}{\frac {1}{1-\kappa ^{2}}}\right]^{3}}{\sigma _{\kappa }^{3}}}\right]}$

Thus, the skewness of the κ-exponential distribution of type II distribution is given by:

${\displaystyle \operatorname {Skew} [X]=-{\frac {2(15\kappa ^{6}+6\kappa ^{4}+2\kappa ^{2}+1)}{\beta ^{3}\sigma _{\kappa }^{3}(\kappa ^{2}-1)^{3}(36\kappa ^{4}-13\kappa ^{2}+1)}}\quad {\text{for}}\quad 0\leq \kappa <1/3}$

or

${\displaystyle \operatorname {Skew} [X]={\frac {2(15\kappa ^{6}+6\kappa ^{4}+2\kappa ^{2}+1)}{(1-9\kappa ^{2})(2\kappa ^{4}+1)}}{\sqrt {\frac {1-4\kappa ^{2}}{1+2\kappa ^{4}}}}\quad {\text{for}}\quad 0\leq \kappa <1/3}$

The skewness of the ordinary exponential distribution is recovered in the limit ${\displaystyle \kappa \rightarrow 0}$.

The quantiles are given by the following expression

${\displaystyle x_{\textrm {quantile}}(F_{\kappa })=\beta ^{-1}\ln _{\kappa }{\Bigg (}{\frac {1}{1-F_{\kappa }}}{\Bigg )}}$

with ${\displaystyle 0\leq F_{\kappa }\leq 1}$, in which the median is the case :

${\displaystyle x_{\textrm {median}}(F_{\kappa })=\beta ^{-1}\ln _{\kappa }(2)}$

The Lorenz curve associated with the κ-exponential distribution of type II is given by:^[2]

${\displaystyle {\mathcal {L}}_{\kappa }(F_{\kappa })=1+{\frac {1-\kappa }{2\kappa }}(1-F_{\kappa })^{1+\kappa }-{\frac {1+\kappa }{2\kappa }}(1-F_{\kappa })^{1-\kappa }}$

The Gini coefficient is

${\displaystyle \operatorname {G} _{\kappa }={\frac {2+\kappa ^{2}}{4-\kappa ^{2}}}}$

The κ-exponential distribution of type II behaves asymptotically as follows:^[2]

${\displaystyle \lim _{x\to +\infty }f_{\kappa }(x)\sim \kappa ^{-1}(2\kappa \beta )^{-1/\kappa }x^{(-1-\kappa )/\kappa }}$

${\displaystyle \lim _{x\to 0^{+}}f_{\kappa }(x)=\beta }$

The κ-exponential distribution has been applied in several areas, such as:

• In geomechanics, for analyzing the properties of rock masses;^[3]
• In quantum theory, in physical analysis using Planck's radiation law;^[4]
• In inverse problems, the κ-exponential distribution has been used to formulate a robust approach;^[5]
• In Network theory.^[6]

• Giorgio Kaniadakis
• Kaniadakis statistics
• Kaniadakis distribution
• Kaniadakis κ-Gaussian distribution
• Kaniadakis κ-Gamma distribution
• Kaniadakis κ-Weibull distribution
• Kaniadakis κ-Logistic distribution
• Kaniadakis κ-Erlang distribution
• Exponential distribution

• Giorgio Kaniadakis Google Scholar page
• Kaniadakis Statistics on arXiv.org