Lucid (programming language)

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: "Lucid" programming language – news · newspapers · books · scholar · JSTOR (April 2018) (Learn how and when to remove this message)

Lucid is a dataflow programming language designed to experiment with non-von Neumann programming models. It was designed by Bill Wadge and Ed Ashcroft and described in the 1985 book Lucid, the Dataflow Programming Language.^[1]

pLucid was the first interpreter for Lucid.

Lucid uses a demand-driven model for data computation. Each statement can be understood as an equation defining a network of processors and communication lines between them through which data flows. Each variable is an infinite stream of values and every function is a filter or a transformer. Iteration is simulated by 'current' values and 'fby' (read as 'followed by') operator allowing composition of streams.

Lucid is based on an algebra of histories, a history being an infinite sequence of data items. Operationally, a history can be thought of as a record of the changing values of a variable, history operations such as first and next can be understood in ways suggested by their names. Lucid was originally conceived as a disciplined, mathematically pure, single-assignment language, in which verification would be simplified. However, the dataflow interpretation has been an important influence on the direction in which Lucid has evolved.[1]

In Lucid (and other dataflow languages) an expression that contains a variable that has not yet been bound waits until the variable has been bound, before proceeding. An expression like x + y will wait until both x and y are bound before returning with the output of the expression. An important consequence of this is that explicit logic for updating related values is avoided, which results in substantial code reduction, compared to mainstream languages.

Each variable in Lucid is a stream of values. An expression n = 1 fby n + 1 defines a stream using the operator 'fby' (a mnemonic for "followed by"). fby defines what comes after the previous expression. (In this instance the stream produces 1,2,3,...). The values in a stream can be addressed by these operators (assuming x is the variable being used):

'first x' - fetches the first value in the stream x,

'x' - the current value of the stream,

'next x' - fetches the next value in the stream.

'asa' - an operator that does some thing 'as soon as' the condition given becomes true.

'x upon p' - upon is an operator that repeats the old value of the stream x, and updates to the new values only when the stream p makes a true value available. (It serves to slow down the stream x) i.e.: x upon p is the stream x with new values appearing upon the truth of p.

The computation is carried out by defining filters or transformation functions that act on these time-varying streams of data.

 fac
   where
     n = 0 fby (n + 1);
     fac = 1 fby ( fac * (n + 1) );
   end

 fib
   where
     fib = 0 fby ( 1 fby fib + next fib );
   end

 total
   where
      total = 0 fby total + x
   end;

 running_avg
   where 
      sum = first(input) fby sum + next(input);
      n = 1 fby n + 1;
      running_avg = sum / n;
   end;

 prime
   where
      prime = 2 fby (n whenever [[isprime]](n));
      n = 3 fby n+1;
      isprime(n) = not(divs) asa divs or prime*prime > N
                      where
                        N is current n;
                        divs = N mod prime eq 0;
                      end;
   end

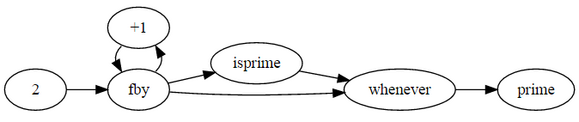 qsort(a) = if eof(first a) then {{not a typo|a}} else follow(qsort(b0),qsort(b1)) fi
   where
      p = first a < a;
      b0 = a whenever p;
      b1 = a whenever not p;
      follow(x,y) = if xdone then y upon xdone else x fi
                      where
                         xdone = iseod x fby xdone or iseod x; 
                      end
   end

     --------> whenever -----> qsort ---------
    |             ^                           |
    |             |                           |
    |            not                          |
    |             ^                           |
    |---> first   |                           |
    |       |     |                           |
    |       V     |                           |
    |---> less ---                            |
    |             |                           |
    |             V                           V
 ---+--------> whenever -----> qsort -----> conc -------> ifthenelse ----->
    |                                                       ^   ^
    |                                                       |   |
     --------> next ----> first ------> iseod --------------    |
    |                                                           |
     -----------------------------------------------------------

 sqroot(avg(square(a)))
   where
      square(x) = x*x;
      avg(y)    = mean
         where
           n = 1 fby n+1;
           mean = first y fby mean + d;
           d = (next y - mean)/(n+1);
         end;
      sqroot(z) = approx asa  err < 0.0001
         where
           Z is current z;
           approx = Z/2 fby (approx + Z/approx)/2;
           err    = abs(square(approx)-Z);
         end;
    end

 h
    where
      h = 1 fby merge(merge(2 * h, 3 * h), 5 * h);
      merge(x,y) = if xx <= yy then xx else yy fi
         where 
           xx = x upon xx <= yy;
           yy = y upon yy <= xx;
         end;
    end;

• pLucid