Tas binaire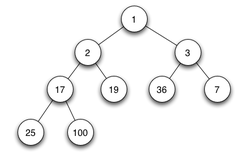

Cet article ne cite pas suffisamment ses sources (mai 2013).

Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».

En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?

En informatique, un tas binaire est une structure de données utilisée notamment pour implémenter une file de priorité car elle permet de retirer l’élément de priorité maximale (resp. minimale) d'un ensemble ou d’insérer un élément dans l'ensemble en temps logarithmique tout en conservant la structure du tas binaire^[1]. On peut la représenter par un arbre binaire qui vérifie ces deux contraintes :

• C'est un arbre binaire complet : tous les niveaux sauf le dernier doivent être totalement remplis et si le dernier ne l'est pas totalement, alors il doit être rempli de gauche à droite.
• C'est un tas : l'étiquette, appelée également clé ou key, de chaque nœud, doit être, soit supérieure ou égale, soit inférieure ou égale aux étiquettes de chacun de ses fils. La signification de supérieur ou égal dépend de la relation d'ordre choisie.

Si la relation d'ordre choisie est "supérieure ou égale", on parle alors de tas-max (ou max-heap). Si la relation est "inférieure ou égale", on parle alors de tas-min (ou min-heap).

Le tas binaire a été introduit par J. W. J. Williams (en) en 1964, en tant que structure de données pour le tri en tas^[2].

Un tas binaire est un arbre binaire parfait. On peut donc l'implémenter, de manière compacte, avec un tableau :

• La racine se situe à l'index ${\displaystyle 0}$
• Étant donné un nœud à l'index ${\displaystyle i}$, son fils gauche est à l'index ${\displaystyle 2i+1}$ et son fils droit à ${\displaystyle 2i+2}$
• Étant donné un nœud à l'index ${\displaystyle i>0}$, son père est à l'index ${\displaystyle \left\lfloor {\frac {i-1}{2}}\right\rfloor }$ (arrondi à l'entier inférieur).

Parfois, dans un souci d'efficacité, on ignore l'indice 0 et place la racine à l'indice 1. Ainsi les indices des fils d'un nœud à l'index ${\displaystyle i}$ sont ${\displaystyle 2i}$ et ${\displaystyle 2i+1}$ et l'indice du père est ${\displaystyle i/2}$.

L'avantage est que le calcul de ces indices peut se faire simplement par des opérations logiques de décalage de bits, ce qui est plus efficace en pratique que des opérations arithmétiques.

Un tas binaire supporte les opérations suivantes :

• Ajouter : ajout d'un élément dans le tas binaire
• Retirer : renvoie la racine et l'enlève du tas
• Augmenter (resp Diminuer) la priorité d'un élément : augmente (resp diminue) la clé de l'élément choisi et modifie l'agencement pour respecter les contraintes de tas binaire
• Construire : construction du tas binaire à partir d'un ensemble d'éléments

Complexité : ${\displaystyle O(\log n)}$

Considérons que l'on veuille ajouter le nœud ${\displaystyle x}$ à notre tas binaire :
On insère ${\displaystyle x}$ à la prochaine position libre, soit la position libre la plus à gauche possible sur le dernier niveau. Puis, on effectue l'opération suivante (que l'on appelle percolation vers le haut ou percolate-up) pour rétablir si nécessaire la propriété d'ordre du tas binaire : tant que ${\displaystyle x}$ n'est pas la racine de l'arbre et que ${\displaystyle x}$ est strictement supérieur à son père, on échange les positions de ${\displaystyle x}$ et son père.

Soit ${\displaystyle h}$ la hauteur de notre tas binaire. Lors de l'algorithme ci-dessus on effectue au plus ${\displaystyle h}$ échanges. Or, comme un tas binaire est un arbre binaire parfait, on a ${\displaystyle h\leq C\times \log n}$, avec ${\displaystyle n}$ le nombre de nœuds du tas binaire et ${\displaystyle C}$ une constante. La complexité est donc bien en ${\displaystyle O(\log n)}$.

Exemple : On insère 50 dans un tas-max.

On insère 50 à la position libre la plus à gauche.

On compare 50 et son père 28. Comme 50 > 28, on échange les positions de 50 et de 28.

On compare 50 et son père 41. Comme 50 > 41, on échange les positions de 50 et 41.

On compare 50 et son père 53. Comme 50 < 53, on n'échange pas les positions de 50 et 53, et on a fini de modifier notre arbre. Il respecte à présent toutes les contraintes d'un arbre binaire.

Complexité : ${\displaystyle O(\log n)}$

On souhaite retirer la racine de notre tas binaire (c'est-à-dire le maximum de notre tas selon la relation d'ordre associée). Cependant, il faut là aussi conserver la structure de tas binaire après la suppression. On procède donc de la manière suivante :
On supprime la racine, et on met à sa place le nœud qui était en dernière position de l'arbre binaire, soit donc le nœud le plus à droite sur le dernier niveau, que l'on notera ${\displaystyle x}$. Puis on fait l'opération suivante (que l'on appelle percolation vers le bas ou percolate-down) : tant que ${\displaystyle x}$ a des fils et que ${\displaystyle x}$ est strictement inférieur à l'un de ses fils, on échange les positions entre ${\displaystyle x}$ et le plus grand de ses fils.

Par le même argument que pour l'algorithme de ajouter, on fait au plus ${\displaystyle h}$ échanges donc la complexité est bien ${\displaystyle O(\log n)}$

Exemple : On retire la racine du tas-max suivant :

On remplace donc la racine par le nœud en dernière position (ici, 20).

On compare 20 et son fils maximum, qui est 41. Comme 41 > 20, on échange 20 et 41.

On compare 20 et son fils maximum, qui est 36. Comme 36 > 20, on échange 20 et 36.

On compare 20 et son fils maximum, qui est 31. Comme 31 > 20, on échange 20 et 31.

20 n'a plus de fils, on a donc fini. Les propriétés d'ordre et de structure du tas sont rétablies.

On peut augmenter ou diminuer la priorité (la clé) d'un nœud mais il faut ensuite satisfaire la contrainte d'ordre. Si l'on augmente la clé on fera donc un percolate-up à partir de notre nœud et si l'on diminue la clé on fera un percolate-down.

Complexité : ${\displaystyle O(h(x))}$ où ${\displaystyle h(x)}$ est la profondeur de ${\displaystyle x}$

On augmente la clé de notre nœud ${\displaystyle x}$, par conséquent il se peut qu'il devienne supérieur à son père et à d'autres nœuds au-dessus de son père. Pour maintenir la contrainte d'ordre on effectue donc l'opération suivante : tant que ${\displaystyle x}$ n'est pas la racine et est strictement supérieur à son père on échange les positions entre ${\displaystyle x}$ et son père.

Complexité : ${\displaystyle O(h-h(x))}$ où ${\displaystyle h(x)}$ est la profondeur de ${\displaystyle x}$ et ${\displaystyle h}$ la hauteur de l'arbre

On diminue la clé de notre nœud ${\displaystyle x}$, il se peut donc qu'il devienne inférieur à un de ses fils et à d'autres nœuds en dessous. Pour maintenir la contrainte d'ordre on effectue donc l'opération suivante : tant que ${\displaystyle x}$ a des fils et est strictement inférieur à un de ses fils on échange les positions entre ${\displaystyle x}$ et son fils maximum.

Complexité : ${\displaystyle O(n)}$

On souhaite construire un tas binaire à partir d'un ensemble d'éléments. De manière naïve on part du tas vide et on ajoute les éléments un par un avec l'algorithme ajouter, ce qui donne une complexité en ${\displaystyle O(n\log n)}$. Ce n'est pas optimal, il existe une manière de construire notre tas binaire en ${\displaystyle O(n)}$ ^[3]:

1. On construit un arbre binaire parfait avec tous les éléments sans se soucier de la contrainte d'ordre. Cela prend donc un temps linéaire en ${\displaystyle n}$.

2. On parcourt les sommets niveau par niveau en partant de l'avant dernier niveau (profondeur ${\displaystyle h-1}$) et dans chaque niveau on parcourt les sommets de la droite vers la gauche. Lors de notre parcours on effectue un percolate-down à partir de chaque sommet.

On convient d'appeler sous-arbre d'un sommet dans un arbre le sous-arbre maximal dont ce sommet est la racine.

Pendant le parcours des sommets on maintient l'invariant suivant : Tous les sous-arbres des sommets à droite du sommet courant (sur le même niveau) sont des tas binaires. Donc après avoir traité la racine, comme elle vérifie l'invariant, notre arbre est un tas binaire.

Soit ${\displaystyle h}$ la hauteur de notre arbre (il y a donc ${\displaystyle h}$ niveaux qui vont de ${\displaystyle 0}$ à ${\displaystyle h-1}$) et ${\displaystyle n}$ le nombre de sommets. Dans le pire cas, chaque percolate-down effectue le nombre maximal d'échange qui est ${\displaystyle h-1-h(x)}$. Le coût total de construire est donc majoré par ${\displaystyle C=\sum _{i=0}^{h-1}2^{i}(h-1-i)}$. Par le changement de variable ${\displaystyle j=h-1-i}$ dans la somme on obtient : ${\displaystyle C=2^{h-1}\sum _{j=1}^{h-1}j{\frac {1}{2^{j}}}}$.
　Or ${\displaystyle j{\frac {1}{2^{j}}}=o({\frac {2^{j}}{3^{j}}})}$ et ${\displaystyle \sum {\frac {2^{j}}{3^{j}}}}$ converge car c'est une série géométrique de raison strictement inférieure à 1. Donc la série ${\displaystyle \sum j{\frac {1}{2^{j}}}}$ converge, d'où ${\displaystyle C=O(2^{h-1})}$. Mais ${\displaystyle 2^{h-2}\leq n}$ donc finalement ${\displaystyle C=O(n)}$.

• Présentation des tas binaires par Lydia Sinapova
• Implémentation en Python

• Portail de l’informatique