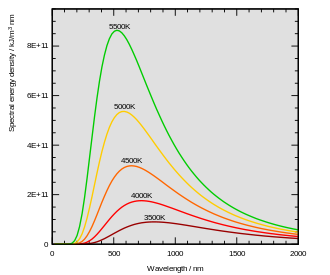
 各温度における黒体輻射のエネルギー密度の波長ごとのスペクトル
各温度における黒体輻射のエネルギー密度の波長ごとのスペクトル
ウィーンの変位則(ウィーンのへんいそく、英: Wien's displacement law)とは、異なる温度の黒体から輻射される電磁波のスペクトルを関係付ける法則である。1893年にヴィルヘルム・ヴィーンによって導かれた。
なお、ヴィーンはドイツの物理学者であるため「ヴィーン」が正しい名称となるが、慣習的に英語読みのウィーンの変位則と呼ばれることも多い。
内容
温度 T で平衡にある空洞輻射が準静的断熱圧縮されたとき、熱力学第2法則から黒体輻射のスペクトルを保ったまま圧縮され、圧縮後は新たな温度 T' での空洞輻射となる。
このとき輻射圧 p = u/3 に抗して仕事を行うので、圧縮比を ε とすれば、エネルギー密度は

に上昇する。
圧縮の前後でシュテファン=ボルツマンの法則 u ∝ T4 が成り立つので、新たな温度は

である。
一方、圧縮に伴うドップラー効果により、波長 λ の輻射は波長が

の輻射へと変化する。
空洞輻射の波長ごとの分光エネルギー密度を  とすれば、二つの温度でのスペクトルの関係は
とすれば、二つの温度でのスペクトルの関係は


で表される。
任意関数 F を用いれば、温度 T、波長 λ での空洞輻射のスペクトルが

と表わされる。
周波数ごとのスペクトル
周波数と波長の関係 ν = c/λ から、周波数 ν の輻射はドップラー効果により

の輻射へと変化する。
周波数ごとの分光エネルギー密度を  とすれば、二つの温度での関係は
とすれば、二つの温度での関係は


で表される。
任意関数 F' を用いれば、温度 T での空洞輻射の周波数 ν ごとのスペクトルが

と表わされる。
スペクトルのピーク
ウィーンの変位則の主な帰結として、スペクトルがピークとなる波長が温度に逆比例することが挙げられる。
比例係数 b を用いてピーク波長が

と表わされる。比例係数 b の値は

である[1]。
また、スペクトルがピークとなる周波数は温度に正比例し、ピーク周波数は

と表わされる。比例係数 b' の値は

である。
例
物体の温度が高ければ、放射される波長は短くなる。例えば、太陽の表面温度 5780 K の場合ピーク波長は 500 nm にある。
白熱電球をみると、温度の低い時、黄色っぽい光になりさらに温度が低い時赤くみえる(色温度も参照)。
比例係数の導出
ウィーンの変位則により黒体輻射のスペクトルの関数形は

に制限される。
スペクトルがピークとなる波長は

で与えられる。
関数 F が任意であるためウィーンの変位則だけでは係数 b を決定することはできないが、プランクの法則により具体的なスペクトル分布が得られており、係数 b を決定することができる。
プランクの法則によれば、黒体輻射の波長ごとの分光エネルギー密度 uλ は

である。
 なので
なので
![{\displaystyle \left.{\frac {dF}{dx}}\right|_{x=b}=b^{-1}F(b)\left[{\frac {c_{2}/b}{1-e^{-c_{2}/b}}}-5\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66219f77a8092ed62afd1bfa21dc8f3d48c721cf)
となり、x > 0 に対して F(x) > 0 なので

である。
この解はランベルトのW関数を用いて

と表されるので

を得る。
別の導出
振動数で表示されたプランクの公式

を用いても、同様の導出が可能である。この場合、x = hνmax/kT は

の解で、

となる。したがってピークにおける振動数は

となる。 ではないことに注意が必要である。
ではないことに注意が必要である。
脚注
- 出典
参考文献
- W.Wien (1893). “Eine neue Beziehung der Strahlung schwarzer Körper zum zwiten Huptsatz der Wärmetheorie”. Ber.d.Berl.Akad..
関連項目




















![{\displaystyle \left.{\frac {dF}{dx}}\right|_{x=b}=b^{-1}F(b)\left[{\frac {c_{2}/b}{1-e^{-c_{2}/b}}}-5\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66219f77a8092ed62afd1bfa21dc8f3d48c721cf)





















