сѓгсЃГсѓбуљєУФќсЂ«тЪ║Тюгт«џуљє
ТЋ░тГдсЂФсЂісЂёсЂдсђЂсѓгсЃГсѓбуљєУФќсЂ«тЪ║Тюгт«џуљє (УІ▒: fundamental theorem of Galois theory) сЂесЂ»сђЂсЂѓсѓІуе«сЂ«СйЊсЂ«ТІАтцДсЂїсЂфсЂЎТДІжђасѓњУеўУ┐░сЂЎсѓІухљТъюсЂДсЂѓсѓІсђѓ т«џуљєсЂ«ТюђсѓѓтЪ║ТюгуџёсЂфСИ╗т╝хсЂ»сђїСйЊсЂ«ТюЅжЎљТгАсѓгсЃГсѓбТІАтцД E/F сЂїСИјсЂѕсѓЅсѓїсѓІсЂесђЂсЂЮсЂ«СИГжќЊСйЊсЂесѓгсЃГсѓбуЙц Gal(E/F) сЂ«жЃетѕєуЙцсЂ«жќЊсЂФСИђт»ЙСИђт»Йт┐юсЂїтГўтюесЂЎсѓІсђЇсЂЊсЂесЂДсЂѓсѓІсђѓ№╝ѕСИГжќЊСйЊсЂесЂ»сђЂF Ріє K Ріє E сѓњТ║ђсЂЪсЂЎСйЊсЂ«сЂЊсЂесѓњУеђсЂєсђЂсЂЮсѓїсѓЅсѓњ E/F сЂ«жЃетѕєТІАтцДсЂеУеђсЂєсђѓ№╝ЅсЂЊсЂ«т«џуљєсЂ»ТІАтцДСйЊ E/F сЂ«СИГжќЊСйЊсЂ«тѕєжАъсЂесЂёсЂєжЏБсЂЌсЂЈУЂъсЂЊсЂѕсѓІтЋЈжАїсѓњсђЂсЂѓсѓІТюЅжЎљуЙцсЂ«жЃетѕєуЙцсѓњтѕЌТїЎсЂЏсѓѕсЂесЂёсЂєсѓѕсѓіТЅ▒сЂёТўЊсЂётЋЈжАїсЂИтцЅТЈЏсЂЌсЂдсЂёсѓІсђѓ Уе╝ТўјтЪ║Тюгт«џуљєсЂ«Уе╝ТўјсЂ»сђЂУЄфТўјсЂфсЂЊсЂесЂДсЂ»сЂфсЂёсђѓжђџтИИсЂ«ТЅ▒сЂёсЂДТюђсѓѓжЄЇУдЂсЂфуѓ╣сЂ»сђЂСИјсЂѕсѓЅсѓїсЂЪУЄфти▒тљїтъІуЙцсЂФсѓѕсѓітЏ║т«џсЂЋсѓїсЂЪСИГжќЊСйЊсЂ«ТгАтЁЃсѓњтѕХтЙАсЂЎсѓІсЂЊсЂесЂїсЂДсЂЇсѓІсЂесЂёсЂєсђЂсѓесЃЪсЃ╝сЃФсЃ╗сѓбсЃФсЃєсѓБсЃ│сЂФсѓѕсѓІт╣Йтѕєу╣іу┤░сЂфухљТъюсЂДсЂѓсѓІсђѓсѓгсЃГсѓбТІАтцД K/F сЂ«УЄфти▒тљїтъІтєЎтЃЈсЂ»сђЂСйЊ K СИісЂ«тЄйТЋ░сЂесЂЌсЂдуиџтъІуІгуФІсЂДсЂѓсѓІсђѓсЂЊсЂ«С║Іт«ЪсЂ»сђЂсѓѕсѓіСИђУѕгуџёсЂфС║Іт«ЪсЂДсЂѓсѓІТїЄТеЎсЂ«уиџтъІуІгуФІТђДсЂІсѓЅтЙЊсЂєсђѓ тјЪтДІтЁЃт«џуљєсѓњСй┐сЂєсЂІсЂфсѓіу░АтЇўсЂфУе╝ТўјсѓѓсЂѓсѓІсЂїсђЂТюЅжЎљСйЊсЂ«та┤тљѕсЂФуЋ░сЂфсѓІ№╝ѕсЂЌсЂІсЂЌсѓѕсѓіу░АтЇўсЂф№╝ЅУе╝ТўјсѓњсЂЎсѓІт┐ЁУдЂсЂїсЂѓсѓІсЂЪсѓЂсђЂуЈЙС╗БуџёсЂфтЈќТЅ▒сЂёсЂДсЂ»сЂ╗сЂесѓЊсЂЕућесЂёсѓЅсѓїсЂфсЂё[1]сђѓ ТійУ▒АуџёсЂфУеђУЉЅсЂДсЂ»сђїсѓгсЃГсѓбт»Йт┐юсЂїтГўтюесЂЎсѓІсђЇсЂеУ┐░сЂ╣сѓЅсѓїсѓІсђѓсЂЮсЂ«тцџсЂЈсЂ«ТђДУ│фсЂ»тЇўсЂФтйбсЂ«СИісЂДсЂ«сЂЊсЂесЂДсЂѓсѓІсЂїсђЂт«ЪжџЏсЂ«жаєт║ЈжЏєтљѕсЂ«тљїтъІтєЎтЃЈсѓњУеўУ┐░сЂЎсѓІсЂФсЂ»сЂёсЂЈсѓЅсЂІСйюТЦГсѓњУдЂсЂЎсѓІсђѓ т»Йт┐юсЂ«Тўјуц║уџёсЂфУеўУ┐░ТюЅжЎљТІАтцДсЂФт»ЙсЂЌсђЂт»Йт┐юсЂ»ТгАсЂ«сѓѕсЂєсЂФТўјуц║уџёсЂФУ┐░сЂ╣сѓІсЂЊсЂесЂїсЂДсЂЇсѓІсђѓ
СЙІсЂѕсЂ░сђЂСИђуЋфСИісЂ«СйЊ E сЂ» Gal(E/F) сЂ«УЄфТўјсЂфжЃетѕєуЙцсЂФт»Йт┐юсЂЌсђЂтЪ║уцјСйЊ F сЂ» Gal(E/F) сЂ«тЁеСйЊсЂФт»Йт┐юсЂЎсѓІсђѓ т»Йт┐юсЂ«ТђДУ│фт»Йт┐юсЂ»ТгАсЂ«сѓѕсЂєсЂфТюЅуЏісЂфТђДУ│фсѓњТїЂсЂБсЂдсЂёсѓІсђѓ
СЙІ СйЊ K = Q(Рѕџ2, Рѕџ3) = Q(Рѕџ2)(Рѕџ3) сѓњУђЃсЂѕсѓІсђѓ K сЂ» Рѕџ2 сЂе Рѕџ3 сѓњжаєсЂФТи╗тіасЂЎсѓІсЂЊсЂесЂДТ▒║т«џсЂЋсѓїсѓІсЂ«сЂДсђЂK сЂ«тљёсђЁсЂ«тЁЃсЂ»ТгАсЂ«сѓѕсЂєсЂФУАесЂЎсЂЊсЂесЂїсЂДсЂЇсѓІсђѓ сЂЊсЂЊсЂФ a, b, c, d сЂ»ТюЅуљєТЋ░сЂДсЂѓсѓІсђѓсЂЊсЂ«сѓгсЃГсѓбуЙц G = Gal(K/Q) сЂ» a сѓњтЏ║т«џсЂЎсѓІсѓѕсЂєсЂф K сЂ«УЄфти▒тљїтъІсѓњУф┐сЂ╣сѓІсЂЊсЂесЂДТ▒║т«џсЂЎсѓІсЂЊсЂесЂїсЂДсЂЇсѓІсђѓсѓгсЃГсѓбуЙцсЂФт▒ъсЂЎсѓІуй«ТЈЏсЂ»Тюђт░ЈтцџжаЁт╝ЈсЂ«Та╣сЂ«тЁЦсѓїТЏ┐сЂѕсЂасЂЉсЂїсЂДсЂЇсѓІсЂ«сЂДсђЂсЂЮсЂ«сѓѕсЂєсЂфУЄфти▒тљїтъІсЂ» Рѕџ2 сѓњ Рѕџ2 сѓѓсЂЌсЂЈсЂ» РѕњРѕџ2 сЂИтєЎсЂЌсђЂРѕџ3 сѓњ Рѕџ3 сѓѓсЂЌсЂЈсЂ» РѕњРѕџ3 сЂИтєЎсЂЎт┐ЁУдЂсЂїсЂѓсѓІсђѓf сЂї Рѕџ2 сЂе РѕњРѕџ2 сЂесѓњтЁЦсѓїТЏ┐сЂѕсѓІсЂесЂЎсѓІсЂесђЂ сЂесЂфсѓісђЂg сЂї Рѕџ3 сЂе РѕњРѕџ3 сѓњтЁЦсѓїТЏ┐сЂѕсѓІсЂесЂЎсѓІсЂесђЂ сЂесЂфсѓІсђѓсЂЊсѓїсѓЅсЂ»ТўјсѓЅсЂІсЂФ K сЂ«УЄфти▒тљїтъІсЂДсЂѓсѓІсђѓСйЋсѓѓтцЅсЂѕсЂфсЂёТЂњуГЅтєЎтЃЈсЂДсЂѓсѓІУЄфти▒тљїтъІ 1 сѓѓтГўтюесЂЌсђЂf сЂе g сЂ«тљѕТѕљсѓѓтГўтюесЂЌсђЂсЂЮсѓїсѓЅсЂ«СИАТќ╣сЂ«тєфТа╣сЂ«угдтЈисѓњтцЅсЂѕсѓІсђѓ сЂЌсЂЪсЂїсЂБсЂд сЂДсЂѓсѓісђЂ G сЂ»сѓ»сЃЕсѓцсЃ│сЂ«тЏЏтЁЃуЙцсЂФтљїтъІсЂДсЂѓсѓІсђѓсЂЊсЂ«уЙцсЂ» 5сЂцсЂ«жЃетѕєуЙцсѓњТїЂсЂАсђЂсЂЮсѓїсѓЅсЂ«тљёсђЁсЂ»тЪ║Тюгт«џуљєсЂІсѓЅ K сЂ«жЃетѕєСйЊсЂет»Йт┐юсЂЎсѓІсђѓ
жЮъсѓбсЃ╝сЃЎсЃФуџёсЂфСЙІ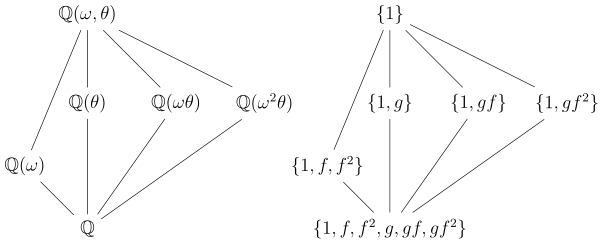 ТгАсЂ«СЙІсЂ»сѓгсЃГсѓбуЙцсЂїсѓбсЃ╝сЃЎсЃФуЙцсЂДсЂфсЂёТюђсѓѓу░АтЇўсЂфСЙІсЂДсЂѓсѓІсђѓ Q СИісЂ«тцџжаЁт╝Ј x3Рѕњ2 сЂ«тѕєУДБСйЊ K сѓњУђЃсЂѕсѓІсђѓсЂЎсЂфсѓЈсЂАсђЂK = Q (╬И, ¤Ѕ) сЂДсђЂсЂЊсЂЊсЂФ ╬И сЂ» 2 сЂ«уФІТќ╣Та╣сЂДсЂѓсѓісђЂ¤Ѕ сЂ» 1 сЂ«уФІТќ╣Та╣сЂДсЂѓсѓІ№╝ѕсЂї 1 сЂДсЂ»сЂфсЂё№╝ЅсђѓСЙІсЂѕсЂ░сђЂK сѓњУцЄу┤аТЋ░сЂ«СИГсЂ«СйЊсЂеУђЃсЂѕсѓІсЂесђЂ╬И сЂесЂЌсЂд 2 сЂ«т«ЪуФІТќ╣Та╣сђЂ¤Ѕ сЂесЂЌсЂд сЂїтЈќсѓїсѓІсђѓсѓгсЃГсѓбуЙц G = Gal(K/Q) сЂ» 6 сЂцсЂ«тЁЃсѓњсѓѓсЂАсђЂ3сЂцсЂ«т»ЙУ▒АсЂ«уй«ТЈЏуЙцсЂетљїтъІсЂДсЂѓсѓІсђѓG сЂ»№╝ѕсЂЪсЂесЂѕсЂ░№╝Ѕ2сЂцсЂ«УЄфти▒тљїтъІРђћРђћ f сЂе g сЂесЂЎсѓІ РђћРђћсЂФсѓѕсѓіућЪТѕљсЂЋсѓїсђЂсЂЮсѓїсѓЅсЂ»ТгАсЂ« ╬И сЂе ¤Ѕ сЂИсЂ«СйюућесЂФсѓѕсѓіт«џсѓЂсѓЅсѓїсѓІсђѓ сЂЌсЂЪсЂїсЂБсЂд сЂДсЂѓсѓІсђѓ G сЂ«жЃетѕєуЙцсЂет»Йт┐юсЂЎсѓІжЃетѕєСйЊсЂ»ТгАсЂ«сѓѕсЂєсЂФсЂфсѓІсђѓ
т┐юућесЂЊсЂ«т«џуљєсЂ»ТІАтцДСйЊ E/F сЂ«СИГжќЊСйЊсЂ«тѕєжАъсЂесЂёсЂєжЏБсЂЌсЂЈУЂъсЂЊсЂѕсѓІтЋЈжАїсѓњсђЂсЂѓсѓІТюЅжЎљуЙцсЂ«жЃетѕєуЙцсѓњтѕЌТїЎсЂЏсѓѕсЂесЂёсЂєсѓѕсѓіТЅ▒сЂёТўЊсЂётЋЈжАїсЂИтцЅТЈЏсЂЌсЂдсЂёсѓІсђѓ СЙІсЂѕсЂ░сђЂСИђУѕгсЂ«С║ћТгАТќ╣уеІт╝ЈсЂ»тєфТа╣сЂФсѓѕсЂБсЂдУДБсЂЉсЂфсЂё№╝ѕсѓбсЃ╝сЃЎсЃФ-сЃФсЃЋсѓБсЃІсЂ«т«џуљєсѓњтЈѓуЁД№╝ЅсЂЊсЂесѓњУе╝ТўјсЂЎсѓІсЂЪсѓЂсђЂсЂЙсЂџТюђтѕЮсЂФсђЂтєфТа╣ТІАтцД№╝ѕ╬▒ сѓњ F сЂ«сЂѓсѓІтЁЃсЂ« n С╣ЌТа╣сЂесЂЌсЂЪсЂесЂЇсЂФ F(╬▒) сЂесЂфсѓІсѓѕсЂєсЂфТІАтцД№╝ЅсЂФсѓѕсѓітЋЈжАїсѓњУеђсЂёТЈЏсЂѕсђЂсЂЊсЂ«тЪ║Тюгт«џуљєсѓњСй┐сЂёсђЂтєфТа╣ТІАтцДсЂ«тЋЈжАїсѓњуЏ┤ТјЦт»Йт┐юсЂДсЂЇсѓІуЙцсЂ«тЋЈжАїсЂИтцЅТЈЏсЂЎсѓІсђѓ сѓ»сЃ│сЃъсЃ╝уљєУФќсЂежАъСйЊУФќсЂ«сѓѕсЂєсЂфуљєУФќсЂ»сђЂсЂЊсЂ«тЪ║Тюгт«џуљєсЂІсѓЅС║ѕТЃ│сЂЎсѓІсЂЊсЂесЂїсЂДсЂЇсѓІсђѓ уёАжЎљТгАТІАтцДсЂ«та┤тљѕсЂЊсЂ«тЪ║Тюгт«џуљєсЂФсЂ»сђЂТГБУдЈТІАтцДсЂДсЂѓсѓітѕєжЏбТІАтцДсЂДсЂѓсѓІуёАжЎљТгАС╗БТЋ░ТІАтцДсЂИжЂЕућесЂДсЂЇсѓІсЃљсЃ╝сѓИсЃДсЃ│сѓѓтГўтюесЂЎсѓІсђѓсЂЊсѓїсЂФсЂ»сђЂсѓгсЃГсѓбуЙцсЂФсѓ»сЃФсЃФСйЇуЏИсЂесЂёсЂєсЂѓсѓІСйЇуЏИТДІжђасѓњт«џуЙЕсЂЎсѓІсЂЊсЂесЂїт┐ЁУдЂсЂДсђЂжќЅжЏєтљѕсЂДсЂѓсѓІжЃетѕєуЙцсЂасЂЉсЂїСИіУеўсЂ«т»Йт┐юсЂежќбжђБсЂЌсЂдсЂёсѓІсђѓ УёџТ│етЈѓУђЃТќЄуї«
|
Portal di Ensiklopedia Dunia






















