ダンツィク・ウルフ分解法 (ダンツィク・ウルフぶんかいほう、ダンツィク・ウルフの分解原理、英 : Dantzig–Wolfe decomposition )とは、特殊な構造を持つ線形計画問題 を解くアルゴリズム の一種である。1960年にジョージ・ダンツィーグ (ダンツィク)およびフィリップ・ウルフ (英語版 ) [ 1] [ 2] [ 3] [ 4] [ 5] [ 6] [ 7]
ダンツィク・ウルフ分解法は列生成法 において大規模線形計画問題を扱いやすい問題へと変形することができる。多くの線形計画問題では反復法の改訂単体法 によって解かれることが多いが、各反復で大多数の列(変数)が基底にはならない。このことから、問題を複数の小さな部分問題へと分割し、それら部分問題の解の一部の列の下で、再び部分問題から列を求めて、元の問題の解を改善することを行っている。
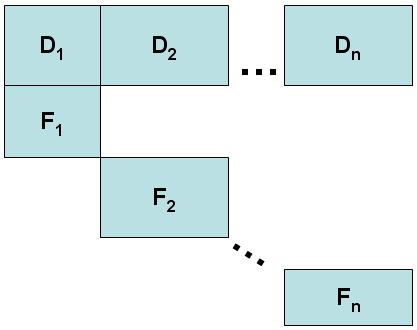
ダンツィク・ウルフ分解法を用いるために、線形計画問題の制約行列が特殊な構造を持っている必要がある。制約の集合の中から多くの変数の係数が非ゼロの値を持つような制約(「接続性」、「連結性」、「複雑化性」)を特定する必要がある。残った他の制約の集合ではそれぞれが独立した部分行列に分割する。すなわち、ある変数が一つの部分行列内において非ゼロの係数を持っているならば、その他の部分行列内においては非ゼロの係数を持たないようにする。これらの構造は以下のように図示される:
D
{\displaystyle D}
F
i
{\displaystyle F_{i}}
F
{\displaystyle F}
必要な形式に表現することができれば、元の問題は主問題と
n
{\displaystyle n}
凸多面体 の任意の点がその多面体の端点 の凸結合 によって表すことができるという事実に基づいて行われている。
新たな主問題の各変数はある部分問題の一つの解に対応している。主問題は部分問題によって表現されている解の組み合わせが連結性などの制約を満たすことを制約として保証する役割を果たしている。また部分問題では通常、解の一部に対応した列のみを保持した状態で表現される。反復において主問題の制約を満たしつつ、元の問題の目的関数値を改善するような部分問題の列を追加していく。
実装上ではいくつかの主流が存在しているが、一般的なダンツィーグ・ウルフ分解法は以下の手順で行われる:
変数が限定された主問題の実行可能解から始め、各部分問題を新たな目的関数に再定式化し、各部分問題によって主問題の現在の目的関数値を改善できるような解を求められると考えられる。
部分問題で実際に新たな目的関数の下で解き直し、その部分問題の最適解を主問題に追加する。
主問題では、各部分問題によって生成された解を全部または一部のみを列(変数)へと追加する。
主問題を単体法により解く。
もし目的関数値が改善されるならば、ステップ1へ戻る。そうでなければ、続ける。
主問題において部分問題からの新たな列によってこれ以上値を改善することができないため、終了。
ダンツィク・ウルフ分解法の実装例としてはAMPL (英語版 ) GAMS のような数理モデリングソフトウェアが挙げられる[ 8] [ 9] JuMP (英語版 ) GNU Linear Programming Kit (英語版 ) オープンソースソフトウェア なども存在している[ 10]
ダンツィク・ウルフ分解法に含まれる各部分問題は互いに独立した問題であるため、それらの問題を並列して解くことが可能である。その場合、主問題では部分問題によって構成された列(変数)をどのように組み合わせるかを考慮する必要がある。主問題は各部分問題の実行が終わるまで待機し、その後目的関数値が改善される変数を新たに導入することが可能であり、またその変数の一部のみを取り入れることも可能である。別の方法としては再定式化後に最初に得られた列のみから始め、その後部分問題の計算を始めるといったことが挙げられる。
また、実装において考えられる選択肢としては各反復において基底から外れる列の扱いについてである。これらの列はその後の反復においても保持されることもあれば、即座に削除することや、以後の反復の後にある基準に従って削除する(例として、十回の反復ごとにすべての非基底列を削除する)ことが挙げられる。
2001年、Tebboth により、並列計算を用いたダンツィク・ウルフ分解法の計算機実験が行われた[ 11]
^ George B. Dantzig ; Philip Wolfe (1960). “Decomposition Principle for Linear Programs”. Operations Research 8 : 101–111. CRID 1360855569262191232 . doi :10.1287/opre.8.1.101 . ISSN 15265463 . NAID 30041574981 . JSTOR 167547 . ^ Dimitris Bertsimas; John N. Tsitsiklis (1997). Introduction to Linear Optimization . Athena Scientific. ISBN 978-1886529199 . NCID BA81051770 . LCCN 96-78786 . OCLC 36686772 ^ George B. Dantzig ; Mukund N. Thapa (1997). Linear Programming 2: Theory and Extensions . Springer . doi :10.1007/b97283 ^ Vašek Chvátal (1983). Linear Programming . Macmillan. ISBN 978-0716715870 ^ Maros, István; Mitra, Gautam (1996). “Simplex algorithms”. In J. E. Beasley. Advances in linear and integer programming . Oxford Science. pp. 1–46. MR 1438309 ^ Maros, István (2003). Computational techniques of the simplex method . International Series in Operations Research & Management Science. 61 . Boston, MA: Kluwer Academic Publishers. pp. xx+325. ISBN 1-4020-7332-1 . MR 1960274 ^ Lasdon, Leon S. (2002). Optimization theory for large systems (reprint of the 1970 Macmillan ed.). Mineola, New York: Dover Publications, Inc.. pp. xiii+523. MR 1888251 ^ “AMPL code repository with Dantzig–Wolfe example ”. 2008年12月26日閲覧。 ^ Kalvelagen, Erwin (May 2003), Dantzig-Wolfe Decomposition with GAMS , http://amsterdamoptimization.com/pdf/dw.pdf 2014年3月31日閲覧。 ^ “Open source Dantzig-Wolfe implementation ”. 2010年10月15日閲覧。 ^ Tebboth, James Richard (2001). A computational study of Dantzig-Wolfe decomposition . http://www.blisworthhouse.co.uk/OR/Decomposition/tebboth.pdf