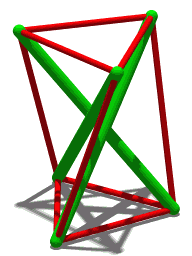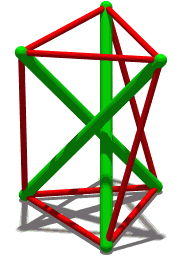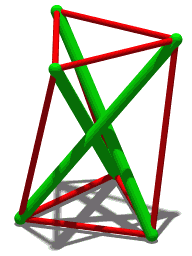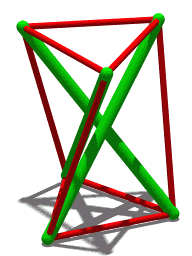
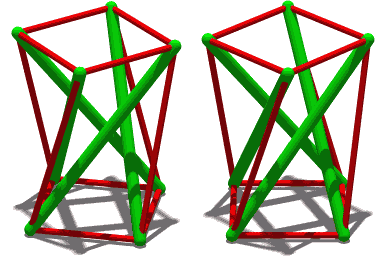
وœ€م‚‚هچکç´”مپھمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و§‹é€ (T3مƒ—مƒھم‚؛مƒ )م€‚3مپ¤مپ®هœ§ç¸®éƒ¨وگ(緑)مپ¯مپم‚Œمپم‚Œن»–مپ®2مپ¤مپ¨ه¯¾ç§°مپ§مپ‚م‚ٹم€پ端مپ‹م‚‰ç«¯مپ¾مپ§ه¯¾ç§°مپ§مپ‚م‚‹م€‚هگ„端مپ¯3وœ¬مپ®م‚±مƒ¼مƒ–مƒ«ï¼ˆèµ¤ï¼‰مپ«وژ¥ç¶ڑمپ•م‚Œمپ¦مپٹم‚ٹم€پمپ“م‚Œم‚‰مپŒه¼µهٹ›م‚’وڈگن¾›مپ—م€پم‚¹م‚«م‚¤مƒمƒ³ مپ®3وœ¬مپ®م‚±مƒ¼مƒ–مƒ«مپŒمپمپ®ه…ˆç´°م‚ٹمپ®وں±مپ®ه؛•ç«¯م‚’ه®ڑ義مپ™م‚‹مپ®مپ¨هگŒمپکو–¹و³•مپ§م€پمپمپ®ç«¯مپ®ن½چç½®م‚’و£ç¢؛مپ«ه®ڑ義مپ™م‚‹م€‚
م‚¹مƒ†مƒ¬م‚ھم‚°مƒ©مƒ
ه†…و–œè¦–é‡ژ(
ن¸¦هˆ—視é‡ژ(
م‚¢مƒ‹مƒ،مƒ¼م‚·مƒ§مƒ³
مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£ï¼ˆtensegrity) مپ¾مپںمپ¯وµ®éپٹهœ§ç¸®ï¼ˆFloating compression) مپ¯م€په¼µهٹ›مپ¨هœ§ç¸®هٹ›مپ®مƒگمƒ©مƒ³م‚¹مپ«م‚ˆمپ£مپ¦و§‹é€ مپŒه®‰ه®ڑمپ™م‚‹م‚·م‚¹مƒ†مƒ مپ§مپ‚م‚‹م€‚و£’çٹ¶مپ®éƒ¨وگ(هœ§ç¸®وگ)مپ¯ن؛’مپ„مپ«وژ¥è§¦مپ›مپڑم€پم‚±مƒ¼مƒ–مƒ«م‚„مƒ¯م‚¤مƒ¤مƒ¼مپھمپ©مپ®ه¼µهٹ›وگمپ«م‚ˆمپ£مپ¦ç©؛ن¸مپ«وµ®مپ‹مپ¶م‚ˆمپ†مپ«é…چç½®مپ•م‚Œم€په…¨ن½“مپ¨مپ—مپ¦هٹ›مپ®وµپم‚ŒمپŒه‡è،،مپ—مپ¦مپ„م‚‹م€‚
軽é‡ڈمپ§وں”è»ںمپھمپŒم‚‰م‚‚ه¼·ه›؛مپھمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و§‹é€ مپ¯م€پن؛؛ن½“مپ®éھ¨و ¼ مپ®م‚ˆمپ†مپھè‡ھ然界مپ‹م‚‰م€په»؛築物م‚„مƒمƒœمƒƒمƒˆه·¥ه¦ م€پçژ©ه…· مپ¨مپ„مپ£مپںن؛؛ه·¥ç‰©مپ¾مپ§ه¹…ه؛ƒمپڈه؟œç”¨مپ•م‚Œمپ¦مپ„م‚‹[ 2] [ 3]
مپ“مپ®ç”¨èھمپ¯1960ه¹´ن»£مپ«ه»؛築ه®¶مپ®مƒگمƒƒم‚¯مƒںمƒ³م‚¹م‚؟مƒ¼مƒ»مƒ•مƒ©مƒ¼ مپ«م‚ˆمپ£مپ¦ه¼µهٹ›çµ±هگˆï¼ˆtensional integrity) مپ®مپ‹مپ°م‚“èھ مپ¨مپ—مپ¦é€ èھ مپ•م‚Œمپں[ 4]
مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£مپ®وœ¬è³ھمپ¯م€پمپ„مپڈمپ¤مپ‹مپ®و§‹é€ هژںçگ†مپ«م‚ˆم‚ٹ特ه¾´مپ¥مپ‘م‚‰م‚Œم‚‹ï¼ڑ
連ç¶ڑه¼µهٹ› ï¼ڑمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£مپ®هں؛وœ¬مپ¨مپ—مپ¦م€په¼µهٹ› è¦پç´ (é€ڑه¸¸مپ¯م‚±مƒ¼مƒ–مƒ«مپ¾مپںمپ¯è…±)مپ¯و§‹é€ ه…¨ن½“م‚’هŒ…م‚€é€£ç¶ڑمƒچمƒƒمƒˆمƒ¯مƒ¼م‚¯م‚’ه½¢وˆگمپ™م‚‹م€‚مپ“م‚Œمپ«م‚ˆم‚ٹو©ںو¢°çڑ„ه؟œهٹ›مپ®ه‡ç‰هˆ†و•£مپŒهڈ¯èƒ½مپ¨مپھم‚ٹم€پو§‹é€ ه½¢çٹ¶م‚’ç¶وŒپمپ—م€پم‚·م‚¹مƒ†مƒ ه…¨ن½“مپ®ه®‰ه®ڑو€§مپ¨وں”è»ںو€§مپ«è²¢çŒ®مپ™م‚‹م€‚ن¸چ連ç¶ڑهœ§ç¸® ï¼ڑو”¯وں±م‚„و£’مپھمپ©مپ®هœ§ç¸®و§‹وˆگè¦پç´ مپ¯م€پن؛’مپ„مپ«ç›´وژ¥وژ¥è§¦مپ›مپڑم€په¼µهٹ›مƒچمƒƒمƒˆمƒ¯مƒ¼م‚¯ه†…مپ«هگٹم‚ٹن¸‹مپ’م‚‰م‚Œمپ¦مپ„م‚‹ç‚¹مپŒç‰¹ه¾´مپ§مپ‚م‚‹م€‚مپ“م‚Œمپ«م‚ˆم‚ٹه‰›و€§وژ¥ç¶ڑمپ®ه؟…è¦پو€§مپŒوژ’除مپ•م‚Œم€پم‚·م‚¹مƒ†مƒ مپ®و§‹é€ هٹ¹çژ‡مپ¨ه¾©ه…ƒهٹ›مپŒهگ‘ن¸ٹمپ™م‚‹م€‚مƒ—مƒ¬م‚¹مƒˆمƒ¬م‚¹ ï¼ڑمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و§‹é€ مپ®é‡چè¦پمپھهپ´é¢مپ¯م€پ組立éپژ程مپ§ه¼µهٹ›è¦پç´ مپŒç· م‚پم‚‰م‚Œم‚‹مƒ—مƒ¬م‚¹مƒˆمƒ¬م‚¹çٹ¶و…‹مپ§مپ‚م‚‹م€‚مƒ—مƒ¬م‚¹مƒˆمƒ¬م‚¹مپ¯و§‹é€ ه‰›و€§مپ¨ه®‰ه®ڑو€§مپ«ه¤§مپچمپڈ貢献مپ—م€پمپ™مپ¹مپ¦مپ®è¦پç´ مپŒه¸¸مپ«ه¼µهٹ›مپ¾مپںمپ¯هœ§ç¸®çٹ¶و…‹مپ«مپ‚م‚‹مپ“مپ¨م‚’ن؟証مپ™م‚‹م€‚è‡ھه·±ه¹³è،، ï¼ڑمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و§‹é€ مپ¯è‡ھه·±ه¹³è،،مپ—مپ¦مپٹم‚ٹم€پو§‹é€ ه…¨ن½“مپ«ه†…部ه؟œهٹ›م‚’è‡ھه‹•çڑ„مپ«هˆ†و•£مپ™م‚‹م€‚مپ“م‚Œمپ«م‚ˆم‚ٹو§‹é€ ه®Œه…¨و€§م‚’ه¤±مپ†مپ“مپ¨مپھمپڈه¤‰ه‹•èچ·é‡چمپ«éپ©ه؟œمپ§مپچم‚‹م€‚وœ€ه°ڈن¸»ç¾©مپ¨هٹ¹çژ‡و€§ ï¼ڑمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£م‚·م‚¹مƒ†مƒ مپ¯وœ€ه°ڈن¸»ç¾©مپ®è¨è¨ˆه“²ه¦م‚’وژ،用مپ—م€پوœ€ه¤§مپ®و§‹é€ ه¼·ه؛¦م‚’éپ”وˆگمپ™م‚‹مپںم‚پمپ«وœ€ه°ڈé‡ڈمپ®وگو–™م‚’هˆ©ç”¨مپ™م‚‹م€‚و‹،ه¼µو€§مپ¨مƒ¢م‚¸مƒ¥مƒ¼مƒ«و€§ ï¼ڑمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£مپ®è¨è¨ˆهژںçگ†مپ¯و‹،ه¼µو€§مپ¨مƒ¢م‚¸مƒ¥مƒ¼مƒ«و§‹é€ م‚’هڈ¯èƒ½مپ«مپ™م‚‹م€‚مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و§‹é€ مپ¯ç‰¹ه®ڑمپ®è¦پن»¶مپ«ه؟œمپکمپ¦م‚µم‚¤م‚؛مپ¨è¤‡é›‘مپ•م‚’ه®¹وک“مپ«éپ©ه؟œمپ¾مپںمپ¯و‹،ه¼µمپ§مپچم‚‹م€‚مپ“مپ®م‚ˆمپ†مپھو§‹é€ çڑ„特ه¾´مپ‹م‚‰م€پهگ„部وگمپ«مپ¯و›²مپ’مƒ¢مƒ¼مƒ،مƒ³مƒˆ م‚„مپ›م‚“و–ه؟œهٹ› مپŒن½œç”¨مپ—مپھمپ„م€‚مپمپ®çµگوœم€پو§‹é€ ه…¨ن½“مپ®è³ھé‡ڈم‚„ن½؟用部وگمپ®و–é¢ç©چمپ«و¯”مپ—مپ¦م€پو¥µم‚پمپ¦é«کمپ„ه¼·ه؛¦مپ¨ه‰›و€§م‚’ه®ںçڈ¾مپ§مپچم‚‹م€‚
مپ“م‚Œم‚‰مپ®هژںçگ†مپŒç·ڈهگˆçڑ„مپ«ن½œç”¨مپ™م‚‹مپ“مپ¨مپ§م€پمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و§‹é€ مپ¯ه¼·ه؛¦م€په¾©ه…ƒهٹ›م€پوں”è»ںو€§مپ¨مپ„مپ†ه„ھم‚Œمپںمƒگمƒ©مƒ³م‚¹م‚’ن¸،ç«‹مپ•مپ›م‚‹م€‚مپ“مپ®ç‰¹و€§مپŒم€په»؛築م€پمƒمƒœمƒƒمƒˆه·¥ه¦م€پç”ںن½“هٹ›ه¦مپ¨مپ„مپ£مپںه¤ڑه²گمپ«م‚ڈمپںم‚‹هˆ†é‡ژمپ§مپ®ه؟œç”¨م‚’هڈ¯èƒ½مپ«مپ—مپ¦مپ„م‚‹مپ®مپ§مپ‚م‚‹م€‚
1951ه¹´:Festival of Britain مپ®م‚¹م‚«م‚¤مƒمƒ³ مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£مپ®و¦‚ه؟µçڑ„و§‹وˆگè¦پç´ مپ¯1951ه¹´مپ®م‚¹م‚«م‚¤مƒمƒ³ مپ«è¦‹م‚‰م‚Œم‚‹م€‚6وœ¬مپ®م‚±مƒ¼مƒ–مƒ« مپŒم€پهگ„端مپ«3وœ¬مپڑمپ¤م€په،”م‚’و‰€ه®ڑن½چç½®مپ«ن؟وŒپمپ—مپ¦مپ„م‚‹م€‚ه؛•éƒ¨مپ«وژ¥ç¶ڑمپ•م‚Œمپں3وœ¬مپ®م‚±مƒ¼مƒ–مƒ«مپŒمپمپ®ن½چç½®م‚’م€Œه®ڑ義م€چمپ—مپ¦مپ„م‚‹م€‚ن»–مپ®3وœ¬مپ®م‚±مƒ¼مƒ–مƒ«مپ¯هچکمپ«مپم‚Œم‚’ه‚ç›´مپ«ن؟مپ£مپ¦مپ„م‚‹م€‚
3و£’مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و§‹é€ (ن¸ٹè¨کمپ®T3مƒ—مƒھم‚؛مƒ مپ®ه›è»¢ه›³مپ«ç¤؛مپ•م‚Œم‚‹ï¼‰مپ¯م€پمپ“مپ®م‚ˆم‚ٹهچکç´”مپھو§‹é€ م‚’هں؛盤مپ¨مپ—مپ¦مپ„م‚‹ï¼ڑهگ„緑色و£’مپ®ç«¯مپ¯م‚¹م‚«م‚¤مƒمƒ³مپ®ن¸ٹ部مپ¨ه؛•éƒ¨مپ®م‚ˆمپ†مپ«è¦‹مپˆم‚‹م€‚ن»»و„ڈمپ®2وœ¬مپ®م‚±مƒ¼مƒ–مƒ«é–“مپ®è§’ه؛¦مپŒ180آ°وœھو؛€مپ§مپ‚م‚‹é™گم‚ٹم€پو£’مپ®ن½چç½®مپ¯وکژç¢؛مپ«ه®ڑ義مپ•م‚Œم‚‹م€‚3وœ¬مپ®م‚±مƒ¼مƒ–مƒ«مپŒه®‰ه®ڑو€§مپ«ه؟…è¦پمپھوœ€ه°ڈé™گمپ§مپ‚م‚‹ن¸€و–¹مپ§م€پç¾ژçڑ„ç›®çڑ„مپ¨ه†—é•·و€§ مپ®مپںم‚پمپ«هگ„مƒژمƒ¼مƒ‰مپ«è؟½هٹ مپ®م‚±مƒ¼مƒ–مƒ«م‚’هڈ–م‚ٹن»کمپ‘م‚‹مپ“مپ¨مپŒمپ§مپچم‚‹م€‚ن¾‹مپˆمپ°م€پم‚±مƒچم‚¹مƒ»م‚¹مƒچمƒ«م‚½مƒ³ (英èھ版 )
م‚¨مƒ¬مƒژم‚¢مƒ»مƒڈمƒ¼مƒˆمƒ‹مƒ¼ (英èھ版 ) [ 5] éپ©ه؟œه‹ه»؛築 (英èھ版 ) [ 6] [ 7]
مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£مپ¯1960ه¹´ن»£مپ«ه»؛築مپ§مپ®ه؟œç”¨مپŒه¢—هٹ مپ—ه§‹م‚پمپںم€‚مƒمƒپم‚§م‚¤مƒ»م‚®مƒ³مƒˆمƒ•مƒˆ مپ¨مƒمƒپم‚§م‚¤مƒ»م‚¯مƒ©م‚·مƒ³م‚¹م‚ مپŒم‚¹مƒمƒ‡م‚¯ م‚¢مƒھمƒ¼مƒٹ複هگˆو–½è¨ï¼ˆمƒمƒ¼مƒ©مƒ³مƒ‰ مپ®م‚«مƒˆمƒ´م‚£مƒ„م‚§ )م‚’è¨è¨ˆمپ—م€پمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£مپ®هژںçگ†م‚’وژ،用مپ—مپںوœ€هˆمپ®ن¸»è¦پو§‹é€ مپ®ن¸€مپ¤مپ¨مپھمپ£مپںم€‚ه±‹و ¹مپ¯م€پمپمپ®ه‘¨ه›²م‚’و”¯وŒپمپ™م‚‹م‚±مƒ¼مƒ–مƒ«م‚·م‚¹مƒ†مƒ مپ«م‚ˆمپ£مپ¦هˆ¶ه¾،مپ•م‚Œم‚‹ه‚¾و–œé¢م‚’ن½؟用مپ—مپ¦مپ„م‚‹م€‚مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£هژںçگ†مپ¯مƒ‡م‚¤مƒ“مƒƒمƒ‰مƒ»م‚¬م‚¤م‚¬مƒ¼ مپ®م‚½م‚¦مƒ«م‚ھمƒھمƒ³مƒ”مƒƒم‚¯ن½“و“چ競وٹ€ه ´ (1988ه¹´ه¤ڈه£م‚ھمƒھمƒ³مƒ”مƒƒم‚¯ 用)مپ¨م‚¸مƒ§مƒ¼م‚¸م‚¢مƒ‰مƒ¼مƒ (1996ه¹´ه¤ڈه£م‚ھمƒھمƒ³مƒ”مƒƒم‚¯ 用)مپ§م‚‚ن½؟用مپ•م‚Œمپںم€‚م‚؟مƒ³مƒ‘مƒ™م‚¤مƒ»مƒ¬م‚¤م‚؛مƒ،م‚¸مƒ£مƒ¼مƒھمƒ¼م‚°é‡ژçگƒمƒپمƒ¼مƒ مپ®وœ¬و‹ هœ°مپ§مپ‚م‚‹مƒˆمƒمƒ”م‚«مƒ¼مƒٹمƒ•م‚£مƒ¼مƒ«مƒ‰ م‚‚م€په¤§مپچمپھمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و§‹é€ مپ«و”¯وŒپمپ•م‚Œمپںمƒ‰مƒ¼مƒ ه±‹و ¹م‚’وŒپمپ£مپ¦مپ„م‚‹م€‚
ن¸–ç•Œوœ€ه¤§مپ®مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و©‹م€پم‚¯مƒھمƒ«مƒ‘و©‹ – مƒ–مƒھم‚¹مƒ™مƒ³ 2009ه¹´10وœˆ4و—¥م€پم‚ھمƒ¼م‚¹مƒˆمƒ©مƒھم‚¢ م‚¯م‚¤مƒ¼مƒ³م‚؛مƒ©مƒ³مƒ‰ه· مپ®مƒ–مƒھم‚¹مƒ™مƒ³ه· مپ«م‚¯مƒھمƒ«مƒ‘و©‹ مپŒé–‹é€ڑمپ—مپںم€‚مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£مپ®هژںçگ†مپ«هں؛مپ¥مپ„مپںه¤ڑé‡چمƒم‚¹مƒˆم€پم‚±مƒ¼مƒ–مƒ«و»هœ¨و§‹é€ مپ§مپ‚م‚ٹم€پçڈ¾هœ¨ن¸–ç•Œوœ€ه¤§مپ®مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و©‹مپ§مپ‚م‚‹م€‚
2014ه¹´:م‚¨م‚¤مƒ م‚؛ç ”ç©¶م‚»مƒ³م‚؟مƒ¼ مپ®م‚¹مƒ¼مƒ‘مƒ¼مƒœمƒ¼مƒ«مƒœمƒƒمƒˆ مپ¯م€پم‚¨م‚¢مƒگمƒƒم‚°مپھمپ—مپ§ن»–مپ®وƒ‘وکںمپ«ç€é™¸مپ—م€پوژ¢وں»مپ®مپںم‚پمپ«ç§»ه‹•هڈ¯èƒ½مپھهˆوœںمƒ—مƒمƒˆم‚؟م‚¤مƒ—مپ§مپ‚م‚‹م€‚مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و§‹é€ مپ¯ç€é™¸è،و’ƒهٹ›م‚’هگ¸هڈژمپ™م‚‹و§‹é€ م‚³مƒ³مƒ—مƒ©م‚¤م‚¢مƒ³م‚¹م‚’وڈگن¾›مپ—م€پم‚±مƒ¼مƒ–مƒ«é•·م‚’ه¤‰و›´مپ™م‚‹مپ“مپ¨مپ§éپ‹ه‹•مپŒéپ©ç”¨مپ•م‚Œم‚‹م€‚ 2000ه¹´ن»£هˆé ن»¥و¥م€پمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£مپ¯è»½é‡ڈمپ§ه¾©ه…ƒهٹ›مپ®مپ‚م‚‹مƒمƒœمƒƒمƒˆم‚’è¨è¨ˆمپ™م‚‹و½œهœ¨èƒ½هٹ›مپ®مپںم‚پمƒمƒœمƒƒمƒˆه·¥ه¦è€…مپ®é–¢ه؟ƒم‚’ه¼•مپ„مپ¦مپ„م‚‹م€‚ه¤ڑو•°مپ®ç ”究مپŒمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£مƒمƒ¼مƒگمƒ¼[ 8] [ 9] [ 10] [ 11] [ 12] م‚¹مƒ¼مƒ‘مƒ¼مƒœمƒ¼مƒ«مƒœمƒƒمƒˆ مپ§مپ‚م‚ٹ[ 13] 6و£’مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و§‹é€ م‚’ن½؟用مپ—مپںه®‡ه®™وژ¢وں»ç”¨مƒمƒ¼مƒگمƒ¼م‚’NASA م‚¨م‚¤مƒ م‚؛ç ”ç©¶م‚»مƒ³م‚؟مƒ¼ مپ§é–‹ç™؛ن¸مپ§مپ‚م‚‹م€‚
م‚¹مƒ†م‚£مƒ¼مƒ–مƒ³مƒ»مƒ¬مƒ“مƒ³مپ«م‚ˆمپ£مپ¦é€ èھمپ•م‚Œمپںمƒگم‚¤م‚ھمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£(Biotensegrity)مپ¯م€پç”ں物ه¦çڑ„و§‹é€ مپ¸مپ®مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£هژںçگ†مپ®و‹،ه¼µçگ†è«–çڑ„ه؟œç”¨مپ§مپ‚م‚‹[ 14] ç‹è‚‰ م€پéھ¨ م€پç‹è†œ م€پéه¸¯ م€پè…± م€پمپ¾مپںمپ¯ه‰›و€§مپٹم‚ˆمپ³ه¼¾و€§ç´°èƒè†œ مپھمپ©مپ®ç”ں物ه¦çڑ„و§‹é€ مپ¯م€په¼µهٹ›éƒ¨هˆ†مپ¨هœ§ç¸®éƒ¨هˆ†مپ®èھ؟ه’Œمپ«م‚ˆمپ£مپ¦ه¼·مپڈمپھم‚‹م€‚ن؛؛é–“مپ®éپ‹ه‹•ه™¨ مپ¯ç‹è‚‰مپ¨çµگهگˆçµ„ç¹”مپ®é€£ç¶ڑمƒچمƒƒمƒˆمƒ¯مƒ¼م‚¯مپ‹م‚‰و§‹وˆگمپ•م‚Œم€پ éھ¨مپ¯ن¸چ連ç¶ڑهœ§ç¸®و”¯وŒپم‚’وڈگن¾›مپ—م€پç¥çµŒç³»مپ¯é›»و°—هˆ؛و؟€م‚’é€ڑمپکمپ¦ç”ںن½“ه†…مپ®ه¼µهٹ›م‚’ç¶وŒپمپ™م‚‹م€‚مƒ¬مƒ“مƒ³مپ¯ن؛؛é–“مپ®è„ٹو¤ژ م‚‚مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و§‹é€ مپ§مپ‚م‚‹مپ¨ن¸»ه¼µمپ—مپ¦مپ„م‚‹مپŒم€پو§‹é€ çڑ„観点مپ‹م‚‰مپ“مپ®çگ†è«–مپ«ه¯¾مپ™م‚‹è£ڈن»کمپ‘مپ¯مپھمپ„[ 16]
مƒ‰مƒٹمƒ«مƒ‰مƒ»Eمƒ»م‚¤مƒ³م‚°مƒگمƒ¼ (英èھ版 ) هˆ†هگç”ں物ه¦ مپ§è¦³ه¯ںمپ•م‚Œم‚‹ه¤ڑو•°مپ®çڈ¾è±،م‚’è¨کè؟°مپ™م‚‹مپںم‚پمپ®مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£çگ†è«–م‚’é–‹ç™؛مپ—مپ¦مپ„م‚‹[ 17] ç´°èƒéھ¨و ¼ م‚’مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£مپ¨مپ—مپ¦è،¨çڈ¾مپ™م‚‹مپ“مپ¨مپ«م‚ˆم‚ٹو•°ه¦çڑ„مپ«مƒ¢مƒ‡مƒ«هŒ–مپ§مپچم‚‹م€‚مپ•م‚‰مپ«م€پè‡ھ然界ه…¨ن½“مپ«è¦‹م‚‰م‚Œم‚‹ه¹¾ن½•ه¦çڑ„مƒ‘م‚؟مƒ¼مƒ³ï¼ˆDNA مپ®م‚‰مپ›م‚“م€پمƒœمƒ«مƒœمƒƒم‚¯م‚¹ مپ®و¸¬هœ°مƒ‰مƒ¼مƒ م€پمƒگمƒƒم‚¯مƒںمƒ³م‚¹م‚؟مƒ¼مƒ•مƒ©مƒ¼مƒ¬مƒ³ مپھمپ©ï¼‰م‚‚م€پهŒ–هگˆç‰©م€پم‚؟مƒ³مƒ‘م‚¯è³ھ[ 18] [ 19] è‡ھ然éپ¸وٹ هœ§هٹ›مپ¯مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و§که¼ڈمپ§çµ„ç¹”مپ•م‚Œمپںç”ں物ه¦çڑ„م‚·م‚¹مƒ†مƒ م‚’ه¥½م‚€هڈ¯èƒ½و€§مپŒé«کمپ„م€‚
م‚¤مƒ³م‚°مƒگمƒ¼مپ«م‚ˆم‚‹èھ¬وکژï¼ڑ
مƒ•مƒ©مƒ¼مپ®مƒ‰مƒ¼مƒ م‚„م‚¹مƒچمƒ«م‚½مƒ³مپ®ه½«هˆ»مپ«ن»£è،¨مپ•م‚Œم‚‹مپ“م‚Œم‚‰مپ®و§‹é€ 物مپ§مپ¯م€په¼µهٹ›م‚’و‹…مپ†éƒ¨وگمپŒم€پéڑ£م‚ٹهگˆمپ†éƒ¨وگهگŒه£«م‚’وœ€çں経路مپ§çµگم‚“مپ§مپ„مپ¾مپ™ï¼ˆمپ“م‚Œمپ¯ه®ڑ義ن¸ٹم€پم‚¸م‚ھمƒ‡م‚·مƒƒم‚¯ï¼ˆو¸¬هœ°ç·ڑçڑ„)مپھé…چç½®مپ¨è¨€مپˆمپ¾مپ™ï¼‰م€‚ه¼µهٹ›مپ¨مپ„مپ†هٹ›مپ¯م€پمپم‚‚مپم‚‚2点間مپ®وœ€çںè·é›¢م‚’ن¼م‚ڈم‚‹و€§è³ھم‚’وŒپمپ£مپ¦مپ„مپ¾مپ™م€‚مپمپ®مپںم‚پم€پمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و§‹é€ مپ®éƒ¨وگمپ¯م€په؟œهٹ›مپ«ه¯¾مپ—مپ¦وœ€م‚‚هٹ¹çژ‡م‚ˆمپڈوٹµوٹ—مپ§مپچم‚‹م‚ˆمپ†مپ«ç²¾ه¯†مپ«é…چç½®مپ•م‚Œمپ¦مپ„م‚‹مپ®مپ§مپ™م€‚مپ“مپ†مپ—مپںçگ†ç”±مپ‹م‚‰م€پمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و§‹é€ مپ¯وœ€ه°ڈمپ®éƒ¨وگمپ§وœ€ه¤§مپ®ه¼·ه؛¦م‚’ç™؛وڈ®مپ™م‚‹مپ“مپ¨مپŒمپ§مپچم‚‹مپ®مپ§مپ™
[ 17] م€‚
ç™؛ç”ںه¦مپ«مپٹمپ„مپ¦م€پمƒھمƒپمƒ£مƒ¼مƒ‰مƒ»م‚´مƒ¼مƒ‰مƒ³ مپ¯èƒڑهˆ†هŒ–و³¢ مپŒم€Œهˆ†هŒ–ه°ڈه™¨ه®کم€چمپ«م‚ˆمپ£مپ¦ن¼و’مپ•م‚Œم‚‹مپ¨وڈگو،ˆمپ—مپں[ 20] ç´°èƒéھ¨و ¼ مپ¯م€Œç´°èƒçٹ¶و…‹هˆ†ه‰²ه™¨م€چمپ¨ه‘¼مپ°م‚Œم‚‹ç´°èƒمپ®é ‚端مپ§هڈŒه®‰ه®ڑمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و§‹é€ مپ«çµ„مپ؟ç«‹مپ¦م‚‰م‚Œم‚‹[ 21]
م‚±مƒچم‚¹مƒ»م‚¹مƒچمƒ«م‚½مƒ³مپ®1948ه¹´Xمƒ¢م‚¸مƒ¥مƒ¼مƒ«è¨è¨ˆم€‚2مپ¤مپ®مƒ¢م‚¸مƒ¥مƒ¼مƒ«مپ®وں±مپ«ه…·ن½“هŒ–مپ—مپ¦مپ„م‚‹ مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£مپ®èµ·و؛گمپ¯وکژç¢؛مپ«مپ¯هˆ†مپ‹مپ£مپ¦مپ„مپھمپ„[ 23] çڑ®é©مƒ•مƒ¬مƒ¼مƒ م‚«مƒ¤مƒƒم‚¯ م‚„éڑœهگ مپھمپ©م€په¤ڑمپڈمپ®ن¼çµ±çڑ„و§‹é€ مپ¯é،ن¼¼مپ®و–¹و³•مپ§ه¼µهٹ›مپ¨هœ§ç¸®è¦پç´ م‚’ن½؟用مپ—مپ¦مپ„م‚‹م€‚
مƒم‚·م‚¢مپ®èٹ¸è،“ه®¶مƒ´م‚£م‚¢مƒپم‚§م‚¹مƒ©مƒ•مƒ»م‚³مƒ¬م‚¤مƒپمƒ¥م‚¯ مپ¯م€پمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£مپ®م‚¢م‚¤مƒ‡م‚¢مپ¯وœ€هˆمپ«م‚«مƒ¼مƒ«مƒھم‚¹مƒ»مƒ¨مƒڈمƒ³م‚½مƒ³م‚¹ (مƒم‚·م‚¢èھمپٹم‚ˆمپ³مƒ‰م‚¤مƒ„èھمپ§م‚«مƒ¼مƒ«مƒ»م‚¤م‚ھم‚¬مƒ³م‚½مƒ³ï¼‰ï¼ˆlv )م€پ1921ه¹´مپ®مƒم‚·م‚¢و§‹وˆگن¸»ç¾© ن¸»è¦په±•è¦§ن¼ڑمپ«ن¸€éƒ¨ن½œه“پم‚’ه¯„ç¨؟مپ—مپںمƒ©مƒˆمƒ“م‚¢ن؛؛ ç³»م‚½مƒ“م‚¨مƒˆم‚¢مƒ´م‚،مƒ³م‚®مƒ£مƒ«مƒ‰ èٹ¸è،“ه®¶مپ«م‚ˆمپ£مپ¦ç™؛وکژمپ•م‚Œمپںمپ¨ن¸»ه¼µمپ—مپں[ 24] مƒمƒھم‚¢مƒ»م‚´مƒ• مپ«م‚ˆمپ£مپ¦و”¯وŒپمپ•م‚Œمپںم€‚ م‚¹مƒچمƒ«م‚½مƒ³مپ¯و§‹وˆگن¸»ç¾©è€…م‚’è‡ھè؛«مپ®ن½œه“پمپ¸مپ®ه½±éں؟مپ¨مپ—مپ¦èھچم‚پمپ¦مپ„م‚‹[ 26] [ 27] [ 28]
1948ه¹´م€پèٹ¸è،“ه®¶مپ®م‚±مƒچم‚¹مƒ»م‚¹مƒچمƒ«م‚½مƒ³ (英èھ版 ) مƒگمƒƒم‚¯مƒںمƒ³م‚¹م‚؟مƒ¼مƒ»مƒ•مƒ©مƒ¼ مپŒè¬›ç¾©مپ—مپ¦مپ„مپں)مƒ–مƒ©مƒƒم‚¯مƒ»مƒم‚¦مƒ³مƒ†مƒ³مƒ»م‚«مƒ¬مƒƒم‚¸ م‚„مپمپ®ن»–مپ®ه ´و‰€مپ§مپ®èٹ¸è،“çڑ„وژ¢و±‚مپ®ه¾Œم€پé©و–°çڑ„مپھم€ŒXمƒ”مƒ¼م‚¹م€چم‚’هˆ¶ن½œمپ—مپںم€‚و•°ه¹´ه¾Œم€پم€Œمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£م€چمپ¨مپ„مپ†ç”¨èھمپ¯و¸¬هœ°مƒ‰مƒ¼مƒ مپ§وœ€م‚‚م‚ˆمپڈçں¥م‚‰م‚Œمپ¦مپ„م‚‹مƒ•مƒ©مƒ¼مپ«م‚ˆمپ£مپ¦é€ èھمپ•م‚Œمپںم€‚مƒ•مƒ©مƒ¼مپ¯çµŒو´م‚’é€ڑمپکمپ¦م€پمƒ€م‚¤مƒم‚¯م‚·مƒ§مƒ³ ن½ڈه®…مپ®و 組مپ؟مپھمپ©مپ§م€پè‡ھè؛«مپ®ن½œه“پمپ«ه¼µهٹ›و§‹وˆگè¦پç´ م‚’組مپ؟è¾¼م‚€ه®ں験م‚’è،Œمپ£مپ¦مپ„مپںم€‚
م‚¹مƒچمƒ«م‚½مƒ³مپ®1948ه¹´مپ®é©و–°مپ¯م€پمƒ•مƒ©مƒ¼مپ«هچ³ه؛§مپ«م‚¹مƒچمƒ«م‚½مƒ³مپ‹م‚‰مƒم‚¹مƒˆم‚’ه§”託مپ•مپ›مپںم€‚1949ه¹´م€پمƒ•مƒ©مƒ¼مپ¯مپ“مپ®وٹ€è،“مپ«هں؛مپ¥مپ„مپ¦مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£-ن؛Œهچپé¢ن½“ م‚’é–‹ç™؛مپ—م€په½¼مپ¨ه¦ç”ںمپںمپ،مپ¯è؟…é€ںمپ«مپ•م‚‰مپھم‚‹و§‹é€ م‚’é–‹ç™؛مپ—م€پمƒ‰مƒ¼مƒ ه»؛è¨مپ«مپ“مپ®وٹ€è،“م‚’éپ©ç”¨مپ—مپںم€‚ن¼‘و¢مپ®ه¾Œم€پم‚¹مƒچمƒ«م‚½مƒ³م‚‚مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و¦‚ه؟µمپ«هں؛مپ¥مپڈه¤ڑو•°مپ®ه½«هˆ»م‚’هˆ¶ن½œمپ™م‚‹م‚ˆمپ†مپ«مپھمپ£مپںم€‚ه½¼مپ®ن¸»è¦پن½œه“پ群مپ¯1959ه¹´مپ«مƒ‹مƒ¥مƒ¼مƒ¨مƒ¼م‚¯è؟‘ن»£ç¾ژè،“館 مپ§é‡چè¦پمپھه±•è¦§ن¼ڑمپŒé–‹ه‚¬مپ•م‚Œمپںمپ¨مپچمپ«ه§‹مپ¾مپ£مپںم€‚MOMAه±•è¦§ن¼ڑمپ§م€پمƒ•مƒ©مƒ¼مپ¯مƒم‚¹مƒˆمپ¨ن»–مپ®ن½œه“پم‚’ه±•ç¤؛مپ—مپ¦مپ„مپں[ 30] ه±•ç¤؛م‚±مƒ¼م‚¹ (英èھ版 )
م‚¹مƒچمƒ«م‚½مƒ³مپ®وœ€م‚‚م‚ˆمپڈçں¥م‚‰م‚Œمپںن½œه“پمپ¯1968ه¹´مپ®26.5-meter-high (87-foot)مپ®م€ژمƒ‹مƒ¼مƒ‰مƒ«م‚؟مƒ¯مƒ¼ (英èھ版 ) [ 32]
ه°‘مپھمپڈمپ¨م‚‚ن¸€éƒ¨مپ®مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و§‹é€ مپ®èچ·é‡چمپ¯م‚ھمƒ¼م‚»مƒ†م‚£مƒƒم‚¯ ه؟œç”مپ¨è² مپ®مƒم‚¢م‚½مƒ³و¯” م‚’ه¼•مپچèµ·مپ“مپ™م€‚ن¾‹مپˆمپ°م€پT3مƒ—مƒھم‚؛مƒ مپ¨6و”¯وں±مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£ن؛Œهچپé¢ن½“مپ§مپ‚م‚‹م€‚
3و£’مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و§‹é€ (3و–¹هگ‘مƒ—مƒھم‚؛مƒ )مپ¯م€پهœ§ç¸®éƒ¨وگم€Œو£’م€چمپ®و‰€ه®ڑمپ®ï¼ˆه…±é€ڑ)長مپ•ï¼ˆهگˆè¨ˆ3وœ¬ï¼‰مپ¨م€پو£’端م‚’وژ¥ç¶ڑمپ™م‚‹ه¼µهٹ›م‚±مƒ¼مƒ–مƒ«م€Œè…±م€چمپ®و‰€ه®ڑمپ®ï¼ˆه…±é€ڑ)長مپ•ï¼ˆهگˆè¨ˆ6وœ¬ï¼‰مپ«ه¯¾مپ—مپ¦م€پéڑ£وژ¥مپ™م‚‹و£’ه؛•éƒ¨مپ¨و£’ن¸ٹ部م‚’وژ¥ç¶ڑمپ™م‚‹è…±مپ®ï¼ˆه…±é€ڑ)長مپ•مپ®ç‰¹ه®ڑه€¤مپŒهکهœ¨مپ—م€پمپ“م‚ŒمپŒو§‹é€ م‚’ه®‰ه®ڑه½¢çٹ¶مپ«ن؟وŒپمپ•مپ›م‚‹مپ¨مپ„مپ†ç‰¹و€§م‚’وŒپمپ¤م€‚مپ“مپ®م‚ˆمپ†مپھو§‹é€ مپ«مپ¤مپ„مپ¦م€پو£’ن¸ٹ部مپ«م‚ˆمپ£مپ¦ه½¢وˆگمپ•م‚Œم‚‹ن¸‰è§’ه½¢مپ¨و£’ه؛•éƒ¨مپ«م‚ˆمپ£مپ¦ه½¢وˆگمپ•م‚Œم‚‹ن¸‰è§’ه½¢مپŒ5د€/6(مƒ©م‚¸م‚¢مƒ³ï¼‰مپ®è§’ه؛¦مپ§ن؛’مپ„مپ«ه›è»¢مپ—مپ¦مپ„م‚‹مپ“مپ¨م‚’証وکژمپ™م‚‹مپ®مپ¯ç›´وژ¥çڑ„مپ§مپ‚م‚‹[ 33]
مپ„مپڈمپ¤مپ‹مپ®2و®µéڑژمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£و§‹é€ مپ®ه®‰ه®ڑو€§ï¼ˆم€Œمƒ—مƒ¬م‚¹مƒˆمƒ¬م‚¹هڈ¯èƒ½و€§م€چ)مپ¯Sultanن»–مپ«م‚ˆمپ£مپ¦هˆ†وگمپ•م‚Œمپ¦مپ„م‚‹[ 34]
T3مƒ—مƒھم‚؛مƒ (مƒˆمƒھمƒ—مƒ¬مƒƒم‚¯م‚¹مپ¨مپ—مپ¦م‚‚çں¥م‚‰م‚Œم‚‹ï¼‰مپ¯م€پç›´ç·ڑن¸‰è§’مƒ—مƒھم‚؛مƒ مپ®ه½¢çٹ¶ç™؛見م‚’é€ڑمپکمپ¦ه¾—م‚‹مپ“مپ¨مپŒمپ§مپچم‚‹م€‚مپمپ®è‡ھه·±ه¹³è،،çٹ¶و…‹مپ¯م€په؛•é¢ن¸‰è§’ه½¢مپŒد€/6مپ®مپمپکم‚ٹ角مپ«م‚ˆمپ£مپ¦هˆ†é›¢مپ•م‚Œمپںه¹³è،Œه¹³é¢مپ«مپ‚م‚‹مپ¨مپچمپ«ن¸ژمپˆم‚‰م‚Œم‚‹م€‚مپمپ®ç‹¬ç‰¹مپھè‡ھه·±ه؟œهٹ›çٹ¶و…‹مپ®ه…¬ه¼ڈمپ¯ن»¥ن¸‹مپ§ن¸ژمپˆم‚‰م‚Œم‚‹[ 35]
د‰
=
د‰
1
[
−
3
,
−
3
,
−
3
,
3
,
3
,
3
,
1
,
1
,
1
,
1
,
1
,
1
]
T
{\displaystyle \omega =\omega _{1}[-{\sqrt {3}},-{\sqrt {3}},-{\sqrt {3}},{\sqrt {3}},{\sqrt {3}},{\sqrt {3}},1,1,1,1,1,1]^{T}}
مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£ن؛Œهچپé¢ن½“مپ®و•°ه¦çڑ„مƒ¢مƒ‡مƒ« è…±مپ¨و”¯وں±مپ®é•·مپ•مپ®و¯”çژ‡مپ«ه؟œمپکمپںمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£ن؛Œهچپé¢ن½“مپ®ç•°مپھم‚‹ه½¢çٹ¶ م‚¹مƒˆمƒمƒ¼مپ¨ç³¸مپ§ن½œم‚‰م‚Œمپںمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£ن؛Œهچپé¢ن½“ 1949ه¹´مپ«م‚¹مƒچمƒ«م‚½مƒ³مپ«م‚ˆمپ£مپ¦وœ€هˆمپ«ç ”究مپ•م‚Œمپںمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£ن؛Œهچپé¢ن½“ مپ¯[ 36] م‚¤م‚§مƒƒم‚»مƒ³مپ®ن؛Œهچپé¢ن½“ مپ¨ه‘¼مپ°م‚Œم‚‹ه¤ڑé¢ن½“مپ®è¾؛مپ«و²؟مپ£مپ¦و”¯وں±مپ¨è…±م‚’وŒپمپ¤م€‚مپ“م‚Œمپ¯ç„،é™گه°ڈ移ه‹•و€§م‚’ن¼´مپ†مپŒه®‰ه®ڑمپ—مپںو§‹é€ مپ§مپ‚م‚‹[ 38] 2d مپ®ç«‹و–¹ن½“م‚’考مپˆم‚‹م€‚هگ„ç«‹و–¹ن½“é¢مپ®ه¹³é¢مپ«é•·مپ•2l مپ®و”¯وں±م‚’é…چç½®مپ—م€پهگ„و”¯وں±مپŒé¢مپ®ن¸€è¾؛مپ¨ه¹³è،Œمپ§é¢مپ®ن¸ه؟ƒمپ«مپ‚م‚‹م‚ˆمپ†مپ«مپ™م‚‹م€‚مپ•م‚‰مپ«م€پهگ„و”¯وں±مپ¯ç«‹و–¹ن½“مپ®هڈچه¯¾é¢مپ®و”¯وں±مپ¨ه¹³è،Œمپ§مپ‚م‚‹مپŒم€پن»–مپ®مپ™مپ¹مپ¦مپ®و”¯وں±مپ¨مپ¯ç›´ن؛¤مپ™م‚‹مپ¹مپچمپ§مپ‚م‚‹م€‚ن¸€مپ¤مپ®و”¯وں±مپ®مƒ‡م‚«مƒ«مƒˆه؛§و¨™مپŒ(0, d, l) مپ¨(0, d, -l) مپ§مپ‚م‚‹ه ´هگˆم€پمپمپ®ه¹³è،Œو”¯وں±مپ®ه؛§و¨™مپ¯مپم‚Œمپم‚Œ(0, -d, -l) مپ¨(0, -d, l) مپ§مپ‚م‚‹م€‚ن»–مپ®و”¯وں±ç«¯ï¼ˆé ‚点)مپ®ه؛§و¨™مپ¯ه؛§و¨™م‚’ç½®وڈ›مپ™م‚‹مپ“مپ¨مپ§ه¾—م‚‰م‚Œم‚‹م€‚ن¾‹مپˆمپ°م€پ(0, d, l)→ (d, l, 0) → (l, 0, d) (立و–¹ن½“مپ®ن¸»ه¯¾è§’ç·ڑمپ§مپ®ه›è»¢ه¯¾ç§°ï¼‰م€‚
ن»»و„ڈمپ®2مپ¤مپ®éڑ£وژ¥مپ™م‚‹é ‚点(0, d , l ) مپ¨(d , l , 0) é–“مپ®è·é›¢s مپ¯
s
2
=
(
d
−
l
)
2
+
d
2
+
l
2
=
2
(
d
−
1
2
l
)
2
+
3
2
l
2
{\displaystyle s^{2}=(d-l)^{2}+d^{2}+l^{2}=2\left(d-{\frac {1}{2}}\,l\right)^{2}+{\frac {3}{2}}\,l^{2}}
و‰€ه®ڑمپ®é•·مپ•2l مپ®و”¯وں±مپ¨و‰€ه®ڑمپ®é•·مپ•s مپ®è…±ï¼ˆéڑ£وژ¥مپ™م‚‹é ‚点م‚’وژ¥ç¶ڑ)مپ§و§‹ç¯‰مپ•م‚Œمپںمپ“مپ®ه›³ه½¢م‚’م€پ
s
>
3
2
l
{\displaystyle s>{\sqrt {\frac {3}{2}}}\,l}
d مپ«ه¯¾مپ—مپ¦2مپ¤مپ®هڈ¯èƒ½مپھه€¤مپŒمپ‚م‚‹مپ“مپ¨م‚’و•™مپˆمپ¦مپ„م‚‹ï¼ڑن¸€مپ¤مپ¯و”¯وں±م‚’وٹ¼مپ—هگˆم‚ڈمپ›م‚‹مپ“مپ¨مپ§ه®ںçڈ¾مپ•م‚Œم€پم‚‚مپ†ن¸€مپ¤مپ¯ه¼•مپچ離مپ™مپ“مپ¨مپ§ه®ںçڈ¾مپ•م‚Œم‚‹م€‚特ه®ڑمپ®ه ´هگˆ
s
=
3
2
l
{\displaystyle s={\sqrt {\frac {3}{2}}}\,l}
d
=
1
2
l
{\displaystyle d={\frac {1}{2}}\,l}
و£ن؛Œهچپé¢ن½“ مپ¨مپ¯ç•°مپھم‚ٹم€پو£ن؛Œهچپé¢ن½“مپ§مپ¯
d
{\displaystyle d}
l
{\displaystyle l}
黄金و¯” مپ«مپھم‚‹م€‚مپ—مپ‹مپ—م€پن¸،و–¹مپ®ه؛§و¨™م‚»مƒƒمƒˆمپ¯ç«‹و–¹ه…«é¢ن½“ مپ‹م‚‰و£ه…«é¢ن½“ (و¥µé™گم‚±مƒ¼م‚¹مپ¨مپ—مپ¦ï¼‰مپ¾مپ§مپ®é€£ç¶ڑçڑ„مپھن½چç½®و—ڈمپ«و²؟مپ£مپ¦هکهœ¨مپ—م€پمپ“م‚Œم‚‰مپ¯م‚‰مپ›م‚“هڈژ縮/و‹،ه¼µه¤‰وڈ›مپ«م‚ˆمپ£مپ¦çµگمپ°م‚Œمپ¦مپ„م‚‹م€‚مپ“مپ®ç«‹و–¹ه…«é¢ن½“مپ®éپ‹ه‹•ه¦ (英èھ版 ) éپ‹ه‹•مپ®ه¹¾ن½•ه¦ مپ§مپ‚م‚‹م€‚مپ“م‚Œمپ¯وœ€هˆمپ«H. S. M. م‚³م‚¯م‚»م‚؟مƒ¼مپ«م‚ˆمپ£مپ¦è¨کè؟°مپ•م‚Œ[ 39] [ 40] [ 41]
مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£ن؛Œهچپé¢ن½“مپ¯ن¸ٹè¨کé–¢ن؟‚مپ®و¥µه€¤ç‚¹م‚’è،¨مپ™مپںم‚پم€پç„،é™گه°ڈ移ه‹•و€§م‚’وŒپمپ¤ï¼ڑè…±مپ®é•·مپ•s مپ®ه°ڈمپ•مپھه¤‰هŒ–(ن¾‹مپˆمپ°è…±م‚’ن¼¸مپ°مپ™مپ“مپ¨مپ«م‚ˆم‚‹ï¼‰مپ¯م€پو”¯وں±مپ®è·é›¢2d مپ®مپ¯م‚‹مپ‹مپ«ه¤§مپچمپھه¤‰هŒ–م‚’م‚‚مپںم‚‰مپ™م€‚
م‚¢مƒ،مƒھم‚«هگˆè،†ه›½ç‰¹è¨±ç¬¬ 3,063,521هڈ· مƒ•مƒ©مƒ³م‚¹ç‰¹è¨±ç¬¬1,377,290هڈ·, "Construction de Reseaux Autotendants", 1964ه¹´9وœˆ28و—¥, مƒ€مƒ“مƒƒمƒ‰مƒ»م‚¸مƒ§مƒ«م‚¸مƒ¥مƒ»م‚¨مƒ،مƒھمƒƒمƒ’.
مƒ•مƒ©مƒ³م‚¹ç‰¹è¨±ç¬¬1,377,291هڈ·, "Structures Linأ©aires Autotendants", 1964ه¹´9وœˆ28و—¥, مƒ€مƒ“مƒƒمƒ‰مƒ»م‚¸مƒ§مƒ«م‚¸مƒ¥مƒ»م‚¨مƒ،مƒھمƒƒمƒ’.
م‚¢مƒ،مƒھم‚«هگˆè،†ه›½ç‰¹è¨±ç¬¬ 3,139,957هڈ· م‚¢مƒ،مƒھم‚«هگˆè،†ه›½ç‰¹è¨±ç¬¬ 3,169,611هڈ· م‚¢مƒ،مƒھم‚«هگˆè،†ه›½ç‰¹è¨±ç¬¬ 3,866,366هڈ·
و™‚مپ«é«که؛¦مپ«وھم‚“مپ هˆ†هگمپ¯م€پم‚مƒ¥مƒگمƒ³ م‚„1.1.1-مƒ—مƒمƒڑمƒ©مƒ³ مپ®م‚ˆمپ†مپ«م€په®¹وک“مپ«م‚¢م‚¯م‚»م‚¹هڈ¯èƒ½مپھهˆ†è§£çµŒè·¯مپŒمپھمپ„مپںم‚پé©ڑمپڈمپ»مپ©ه®‰ه®ڑمپ§مپ‚م‚‹هڈ¯èƒ½و€§مپŒمپ‚م‚‹م€‚
^ “م€Œمƒˆمƒ©مƒ³م‚¹مƒ•م‚©مƒ¼مƒمƒ¼م€چو–°م‚·مƒھمƒ¼م‚؛م€ŒMPGم€چه§‹ه‹•ï¼پ第1ه¼¾مپ¯مƒˆمƒ¬م‚¤مƒ³مƒœمƒƒمƒˆمپ®م‚·مƒ§م‚¦م‚ MPM第12ه¼¾م€Œم‚ھمƒ—مƒ†م‚£مƒم‚¹مƒ—مƒ©م‚¤مƒ م€چمپ¨م€Œهڈچé‡چهٹ›هڈ°ه؛§مƒ†مƒ³م‚»م‚°مƒ™مƒ¼م‚¹م€چ3製ه“پم‚‚ç™؛ه£²و±؛ه®ڑï¼پ â€. HOBBY Watch . و ھه¼ڈن¼ڑ社م‚¤مƒ³مƒ—مƒ¬م‚¹ (2021ه¹´10وœˆ7و—¥). 2022ه¹´2وœˆ9و—¥é–²è¦§م€‚ ^ “مƒˆمƒ©مƒ³م‚¹مƒ•م‚©مƒ¼مƒمƒ¼ مƒ†مƒ³م‚»م‚°مƒ™مƒ¼م‚¹ï½œمƒˆمƒ©مƒ³م‚¹مƒ•م‚©مƒ¼مƒمƒ¼م‚ھمƒ•م‚£م‚·مƒ£مƒ«م‚µم‚¤مƒˆï½œم‚؟م‚«مƒ©مƒˆمƒںمƒ¼ â€. مƒˆمƒ©مƒ³م‚¹مƒ•م‚©مƒ¼مƒمƒ¼م‚ھمƒ•م‚£م‚·مƒ£مƒ«م‚µم‚¤مƒˆ . م‚؟م‚«مƒ©مƒˆمƒںمƒ¼. 2022ه¹´2وœˆ9و—¥é–²è¦§م€‚ ^ Swanson, RL (2013). “Biotensegrity: a unifying theory of biological architecture with applications to osteopathic practice, education, and research-a review and analysisâ€. The Journal of the American Osteopathic Association 113 (1): 34–52. doi :10.7556/jaoa.2013.113.1.34 . PMID 23329804 . ^ Hartley, Eleanor (19 February - 21 March 2009), “Ken Snelson and the Aesthetics of Structureâ€, Kenneth Snelson: Selected Work: 1948–2009 (exhibition catalogue), Marlborough Gallery ^ Korkmaz, Bel Hadj Ali & Smith 2011 ^ Korkmaz, Bel Hadj Ali & Smith 2012 ^ Sabelhaus, Andrew P.; Bruce, Jonathan; Caluwaerts, Ken; Manovi, Pavlo; Firoozi, Roya Fallah; Dobi, Sarah; Agogino, Alice M.; SunSpiral, Vytas (May 2015). “System design and locomotion of SUPERball, an untethered tensegrity robot†. 2015 IEEE International Conference on Robotics and Automation (ICRA) . Seattle, WA, USA: IEEE. pp. 2867–2873. doi :10.1109/ICRA.2015.7139590 . hdl :2060/20160001750 ISBN 978-1-4799-6923-4 . https://ieeexplore.ieee.org/document/7139590 ^ Lessard, Steven; Castro, Dennis; Asper, William; Chopra, Shaurya Deep; Baltaxe-Admony, Leya Breanna; Teodorescu, Mircea; SunSpiral, Vytas; Agogino, Adrian (October 2016). “A bio-inspired tensegrity manipulator with multi-DOF, structurally compliant joints†. 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) . IEEE. pp. 5515–5520. arXiv :1604.08667 . doi :10.1109/iros.2016.7759811 . ISBN 978-1-5090-3762-9 . http://dx.doi.org/10.1109/iros.2016.7759811 ^ Zappetti, Davide; Arandes, Roc; Ajanic, Enrico; Floreano, Dario (2020-06-05). “Variable-stiffness tensegrity spine†. Smart Materials and Structures 29 (7): 075013. Bibcode : 2020SMaS...29g5013Z . doi :10.1088/1361-665x/ab87e0 . ISSN 0964-1726 . https://doi.org/10.1088/1361-665X/ab87e0 . ^ Liu, Yixiang; Dai, Xiaolin; Wang, Zhe; Bi, Qing; Song, Rui; Zhao, Jie; Li, Yibin (2022). “A Tensegrity-Based Inchworm-Like Robot for Crawling in Pipes With Varying Diameters†. IEEE Robotics and Automation Letters 7 (4): 11553–11560. doi :10.1109/LRA.2022.3203585 . ISSN 2377-3766 . https://ieeexplore.ieee.org/document/9873907 . ^ Zappetti, D.; Mintchev, S.; Shintake, J.; Floreano, D. (2017), “Bio-inspired Tensegrity Soft Modular Robotsâ€, Biomimetic and Biohybrid Systems (Cham: Springer International Publishing): pp. 497–508, arXiv :1703.10139 , doi :10.1007/978-3-319-63537-8_42 , ISBN 978-3-319-63536-1 ^ “Super Ball Bot â€. NASA (2015ه¹´4وœˆ2و—¥). 2020ه¹´6وœˆ18و—¥é–²è¦§م€‚ ^ Levin, Stephen (2015). “16. Tensegrity, The New Biomechanics†. In Hutson, Michael; Ward, Adam. Oxford Textbook of Musculoskeletal Medicine . Oxford University Press. pp. 155–56, 158–60. ISBN 978-0-19-967410-7 . https://books.google.com/books?id=u5G1CgAAQBAJ&pg=PA150 ^ Levin, Stephen M. (2002-09-01). “The tensegrity-truss as a model for spine mechanics: biotensegrityâ€. Journal of Mechanics in Medicine and Biology 02 (3n04): 375–88. doi :10.1142/S0219519402000472 . ISSN 0219-5194 . ^ a b Ingber, Donald E. (January 1998). “The Architecture of Life†. Scientific American 278 (1): 48–57. Bibcode : 1998SciAm.278a..48I . doi :10.1038/scientificamerican0198-48 . PMID 11536845 . م‚ھمƒھم‚¸مƒٹمƒ« مپ®2005-05-15و™‚点مپ«مپٹمپ‘م‚‹م‚¢مƒ¼م‚«م‚¤مƒ–م€‚. https://web.archive.org/web/20050515040403/http://web1.tch.harvard.edu/research/ingber/PDF/1998/SciAmer-Ingber.pdf .
^ Edwards, Scott A.; Wagner, Johannes; Grأ¤ter, Frauke (2012). “Dynamic Prestress in a Globular Protein†. PLOS Computational Biology 8 (5): e1002509. Bibcode : 2012PLSCB...8E2509E . doi :10.1371/journal.pcbi.1002509 . PMC 3349725 . PMID 22589712 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3349725/ . ^ Skelton, Robert (2016). “Globally stable minimal mass compressive tensegrity structures†. Composite Structures 141 : 346–54. doi :10.1016/j.compstruct.2016.01.105 . http://www.sciencedirect.com/science/article/pii/S0263822316300174 . ^ Gordon, Natalie K.; Gordon, Richard (2016). “The organelle of differentiation in embryos: The cell state splitter†. Theoretical Biology and Medical Modelling 13 : 11. doi :10.1186/s12976-016-0037-2 . PMC 4785624 . PMID 26965444 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4785624/ . ^ Gordon, Richard (1999). The Hierarchical Genome and Differentiation Waves . Series in Mathematical Biology and Medicine. 3 . doi :10.1142/2755 . ISBN 978-981-02-2268-0 ^ Gأ³mez-Jأ،uregui, V. (2009). “Controversial Origins of Tensegrity†. International Association of Spatial Structures IASS Symposium 2009, Valencia . http://www.tensegridad.es/Publications/Controversial_Origins_Of_Tensegrity_by_GOMEZ-JAUREGUI.pdf . ^ Droitcour, Brian (2006ه¹´8وœˆ18و—¥). “Building Blocks â€. The Moscow Times م‚ھمƒھم‚¸مƒٹمƒ« م‚ˆم‚ٹم‚¢مƒ¼م‚«م‚¤مƒ–م€‚2011ه¹´3وœˆ28و—¥é–²è¦§م€‚ “With an unusual mix of art and science, Vyacheslav Koleichuk resurrected a legendary 1921 exhibition of Constructivist art.†^ م‚¹مƒچمƒ«م‚½مƒ³مپ®Lalvaniم€پ1996ه¹´مپ®è¨کن؛‹مپ§م€پç§پمپ¯ن؟،مپکمپ¦مپ„م‚‹م€‚[è¦پو–‡çŒ®ç‰¹ه®ڑ詳細وƒ…ه ±
^ David Georges Emmerich, Structures Tendues et Autotendantes , Paris: Ecole d'Architecture de Paris la Villette, 1988, pp. 30–31.
^ Gأ³mez-Jأ،uregui, V. et al. (2023) "Tensegrity Applications to Architecture, Engineering and Robotics: A Review Archived 2024-01-19 at the Wayback Machine .&rdquo. Appl. Sci. 2023, 13(15), 8669; https://doi.org/10.3390/app13158669
^ م€ژPortfolio and Art News Annualم€ڈ(No. 4)مپ®1961ه¹´مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£è¨کن؛‹مپ§مپ®مپ“مپ®ه±•è¦§ن¼ڑمپ§مپ®مƒ•مƒ©مƒ¼مپ®ن½œه“پمپ®ه†™çœںم‚’هڈ‚ç…§م€‚
^ “Needle tower â€. 2025ه¹´6وœˆ8و—¥é–²è¦§م€‚ ^
Burkhardt, Robert William Jr. (2008), A Practical Guide to Tensegrity Design م‚ھمƒھم‚¸مƒٹمƒ« مپ®2004-12-20و™‚点مپ«مپٹمپ‘م‚‹م‚¢مƒ¼م‚«م‚¤مƒ–م€‚, https://web.archive.org/web/20041220180510/http://www.angelfire.com/ma4/bob_wb/tenseg.pdf
^
Sultan, Cornel; Martin Corless; Robert E. Skelton (2001). “The prestressability problem of tensegrity structures: some analytical solutions†. International Journal of Solids and Structures 26 : 145. م‚ھمƒھم‚¸مƒٹمƒ« مپ®23 October 2015و™‚点مپ«مپٹمپ‘م‚‹م‚¢مƒ¼م‚«م‚¤مƒ–م€‚. https://web.archive.org/web/20151023184609/http://www.aoe.vt.edu/people/webpages/csultan/publications-pdfs/journalarticleijss2001.pdf .
^ Aloui, Omar; Flores, Jessica; Orden, David; Rhode-Barbarigos, Landolf (2019-04-01). “Cellular morphogenesis of three-dimensional tensegrity structures†(英èھ). Computer Methods in Applied Mechanics and Engineering 346 : 85–108. arXiv :1902.09953 . Bibcode : 2019CMAME.346...85A . doi :10.1016/j.cma.2018.10.048 . ISSN 0045-7825 . https://www.sciencedirect.com/science/article/pii/S0045782518305814 . ^ Cera, Angelo Brian Micubo (2020). Design, Control, and Motion Planning of Cable-Driven Flexible Tensegrity Robots ^ “Tensegrity Figuren â€. Universitأ¤t Regensburg. 2013ه¹´5وœˆ26و—¥و™‚点مپ®م‚ھمƒھم‚¸مƒٹمƒ« م‚ˆم‚ٹم‚¢مƒ¼م‚«م‚¤مƒ–م€‚2013ه¹´4وœˆ2و—¥é–²è¦§م€‚ ^ Coxeter, H.S.M. (1973). “3.7 Coordinates for the vertices of the regular and quasi-regular solidsâ€. Regular Polytopes (3rd ed.). New York: Dover. pp. 51–52 ^ Archived at Ghostarchive and the Wayback Machine : Fuller, R. Buckminster (2010-10-22), Vector Equilibrium , https://www.youtube.com/watch?v=9sM44p385Ws 2019ه¹´2وœˆ22و—¥é–²è¦§م€‚
^ Verheyen, H.F. (1989). “The complete set of Jitterbug transformers and the analysis of their motionâ€. Computers & Mathematics with Applications 17, 1-3 (1–3): 203–250. doi :10.1016/0898-1221(89)90160-0 .
Fuller, R. Buckminster (1961). “Tensegrity†. Portfolio and Art News Annual (4): 112–127, 144, 148. http://www.rwgrayprojects.com/rbfnotes/fpapers/tensegrity/tenseg01.html .   (1982). Synergetics: Explorations in the Geometry of Thinking I . Macmillan. ISBN 978-0-02-065320-2 . https://books.google.com/books?id=AKDgDQAAQBAJ   (1983). Synergetics 2: Further Explorations in the Geometry of Thinking 2 . Macmillan. ISBN 978-0-02-092640-5 . https://books.google.com/books?id=Op4qDwAAQBAJ م‚ھمƒ³مƒ©م‚¤مƒ³  ; Marks, Robert W. (1973). The Dymaxion World of Buckminster Fuller ISBN 978-0-385-01804-3 . https://books.google.com/books?id=X3pRAAAAMAAJ Kenner, Hugh (1976). Geodesic Math and How to Use It ISBN 978-0-520-02924-8 . https://archive.org/details/geodesicmathhowt0000kenn ISBN 0520239318 . مپ“م‚Œمپ¯مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£مپ®و•°ه¦م‚’ه¦مپ³م€پو¨،ه‹م‚’و§‹ç¯‰مپ™م‚‹مپںم‚پمپ®è‰¯مپ„ه‡؛ç™؛点مپ§مپ‚م‚‹م€‚Gأ³mez-Jأ،uregui, Valentin (2007) (م‚¹مƒڑم‚¤مƒ³èھ). Tensegridad. Estructuras Tensegrأticas en Ciencia y Arte . Santander: Universidad de Cantabria. ISBN 978-84-8102-437-1   (2010). Tensegrity Structures and their Application to Architecture . Santander: Servicio de Publicaciones de la Universidad de Cantabria. ISBN 978-84-8102-575-0 Gough, Maria (Spring 1998). “In the Laboratory of Constructivism: Karl Ioganson's Cold Structuresâ€. October 84 : 90–117. doi :10.2307/779210 . JSTOR 779210 . Juan, S. J.; Tur, J M (July 2008). “Tensegrity frameworks: Static analysis reviewâ€. Mechanism and Machine Theory 43 (7): 859–81. doi :10.1016/j.mechmachtheory.2007.06.010 . Korkmaz, Sinan; Bel Hadj Ali, Nizar; Smith, Ian F.C. (June 2011). “Determining Control Strategies for Damage Tolerance of an Active Tensegrity Structure†. Engineering Structures 33 (6): 1930–1939. Bibcode : 2011EngSt..33.1930K . doi :10.1016/j.engstruct.2011.02.031 . م‚ھمƒھم‚¸مƒٹمƒ« مپ®29 September 2011و™‚点مپ«مپٹمپ‘م‚‹م‚¢مƒ¼م‚«م‚¤مƒ–م€‚. https://web.archive.org/web/20110929164401/http://infoscience.epfl.ch/record/164609/files/Korkmaz%20et%20al,%20Determining%20Control%20Strategies%20for%20Damage%20Tolerance%20of%20an%20Active%20Tensegrity%20Structure,%20Engineering%20Structures%20(2011)_2.pdf . Korkmaz, Sinan; Bel Hadj Ali, Nizar; Smith, Ian F.C. (January 2012). “Configuration of Control System for Damage Tolerance of a Tensegrity Bridge†. Advanced Engineering Informatics 26 (1): 145–155. doi :10.1016/j.aei.2011.10.002 . http://infoscience.epfl.ch/record/175523 . Lalvani, Haresh, ed (1996). “Origins of Tensegrity: Views of Emmerich, Fuller and Snelson†. International Journal of Space Structures 11 (1–2): 27–55. doi :10.1177/026635119601-204 . http://journals.sagepub.com/toc/spsa/11/1-2 . Souza, Thales R.; Fonseca, Sأ©rgio T.; Gonأ§alves, Gabriela G.; Ocarino, Juliana M.; Mancini, Marisa C. (October 2009). “Prestress revealed by passive co-tension at the ankle jointâ€. Journal of Biomechanics 42 (14): 2374–80. doi :10.1016/j.jbiomech.2009.06.033 . PMID 19647832 .
Edmondson, Amy (2007). "A Fuller Explanation" , Emergent World LLC
Forbes, Peter (2010). “9. The Push and Pull Building System†. The Gecko's Foot: How Scientists are Taking a Leaf from Nature's Book . Harper Collins. pp. 197–230. ISBN 978-0-00-740547-3 . https://books.google.com/books?id=Vm7MK6Zp6S0C Hanaor, Ariel (1997). “13. Tensegrity: Theory and Application†. In Gabriel, J. Franأ§ois. Beyond the Cube: The Architecture of Space Frames and Polyhedra . Wiley. pp. 385–408. ISBN 978-0-471-12261-6 . https://books.google.com/books?id=FkM0945nFV8C&pg=PA385 Masic, Milenko; Skelton, Robert E.; Gill, Philip E. (August 2005). “Algebraic tensegrity form-findingâ€. International Journal of Solids and Structures 42 (16–17): 4833–4858. doi :10.1016/j.ijsolstr.2005.01.014 . ç·ڑه½¢ه¤‰وڈ› م‚‚مپ¾مپںمƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£مپ§مپ‚م‚‹مپ¨مپ„مپ†و³¨ç›®مپ™مپ¹مپچçµگوœم‚’وڈگç¤؛مپ—مپ¦مپ„م‚‹م€‚Morgan, G.J. (2003). “Historical Review: Viruses, Crystals and Geodesic Domesâ€. Trends in Biochemical Sciences 28 (2): 86–90. doi :10.1016/S0968-0004(02)00007-5 . PMID 12575996 . Motro, R. (1992). “Tensegrity Systems: The State of the Artâ€. International Journal of Space Structures 7 (2): 75–84. doi :10.1177/026635119200700201 . Pugh, Anthony (1976). An Introduction to Tensegrity ISBN 978-0-520-03055-8 . م‚ھمƒھم‚¸مƒٹمƒ« مپ®4 May 2008و™‚点مپ«مپٹمپ‘م‚‹م‚¢مƒ¼م‚«م‚¤مƒ–م€‚. https://web.archive.org/web/20080504081841/http://www.antiqbook.com/boox/vel/29501.shtml 2008ه¹´5وœˆ9و—¥é–²è¦§م€‚ Snelson, Kenneth (November 1990). “Letter to R. Motro†. International Journal of Space Structures . http://www.grunch.net/snelson/rmoto.html . Vilnay, Oren (1990). Cable Nets and Tensegric Shells: Analysis and Design Applications , New York: Ellis Horwood Ltd.
Wang, Bin-Bing (1998). “Cable-strut systems: Part I – Tensegrityâ€. Journal of Constructional Steel Research 45 (3): 281–89. doi :10.1016/S0143-974X(97)00075-8 . Wilken, Timothy (2001). Seeking the Gift Tensegrity , TrustMark
م‚¦م‚£م‚مƒ،مƒ‡م‚£م‚¢مƒ»م‚³مƒ¢مƒ³م‚؛مپ«مپ¯م€پ
مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£ مپ«é–¢é€£مپ™م‚‹م‚«مƒ†م‚´مƒھمپŒمپ‚م‚ٹمپ¾مپ™م€‚







![{\displaystyle \omega =\omega _{1}[-{\sqrt {3}},-{\sqrt {3}},-{\sqrt {3}},{\sqrt {3}},{\sqrt {3}},{\sqrt {3}},1,1,1,1,1,1]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdf881ba88de87799c28d2fcb13c5b26fe0febf2)









![م‚«مƒ¼مƒ«مƒ»م‚¤م‚ھم‚¬مƒ³م‚½مƒ³مپ«م‚ˆم‚‹مƒ—مƒمƒˆمƒ»مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£مƒ—مƒھم‚؛مƒ م€پ1921ه¹´[gallery 1]](http://upload.wikimedia.org/wikipedia/commons/thumb/6/6b/Proto-Tensegrity_by_Ioganson.jpg/120px-Proto-Tensegrity_by_Ioganson.jpg)
![مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£ن؛Œهچپé¢ن½“م€پمƒگمƒƒم‚¯مƒںمƒ³م‚¹م‚؟مƒ¼مƒ»مƒ•مƒ©مƒ¼م€پ1949ه¹´[gallery 2]](http://upload.wikimedia.org/wikipedia/commons/thumb/9/95/Tensegrity_Icosahedron.png/120px-Tensegrity_Icosahedron.png)
![مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£ه››é¢ن½“م€پمƒ•مƒ©مƒ³مƒپم‚§م‚¹م‚³مƒ»مƒ‡مƒƒمƒ©مƒ»م‚µمƒƒمƒ©م€پ1952ه¹´[gallery 3]](http://upload.wikimedia.org/wikipedia/commons/thumb/a/af/Tensegrity_Tetrahedron.png/120px-Tensegrity_Tetrahedron.png)
![مƒ†مƒ³م‚»م‚°مƒھمƒ†م‚£Xمƒ¢م‚¸مƒ¥مƒ¼مƒ«ه››é¢ن½“م€پم‚±مƒچم‚¹مƒ»م‚¹مƒچمƒ«م‚½مƒ³م€پ1959ه¹´[gallery 4]](http://upload.wikimedia.org/wikipedia/commons/thumb/0/07/Tensegrity_X-Module_Tetrahedron.png/120px-Tensegrity_X-Module_Tetrahedron.png)

















