 p, q, r, s, A, C гБЃеА§гБЛгВЙеЫЫиІТ嚥гБЃйЭҐз©НгБМж±ВгБЊгВЛгАВ
p, q, r, s, A, C гБЃеА§гБЛгВЙеЫЫиІТ嚥гБЃйЭҐз©НгБМж±ВгБЊгВЛгАВ
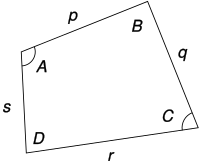
гГЦгГђгГЉгГИгВЈгГ•гГКгВ§гГАгГЉгБЃеЕђеЉПпЉИгГЦгГђгГЉгГИгВЈгГ•гГКгВ§гГАгГЉгБЃгБУгБЖгБЧгБНгАБBretschneider's formulaпЉЙгБѓгАБеЫЫиІТ嚥гБЃйЭҐз©НгВТдЄОгБИгВЛеЕђеЉПгБІгБВгВЛгАВеЫЫиІТ嚥ABCD гБЂгБ§гБДгБ¶гАБp, q, r, s гВТгБЭгВМгБЮгВМгБЃиЊЇгБЃйХЈгБХгАБT гВТеНКеС®йХЈгАБA гБ® C гВТдЇТгБДгБЂеѓЊиІТгБ®гБЩгВЛгБ®гАБеЫЫиІТ嚥гБЃйЭҐз©НгБѓ

гБЂз≠ЙгБЧгБДгАВеЖЖгБЂеЖЕжО•гБЩгВЛеЫЫиІТ嚥гБЃйЭҐз©НгВТи°®гБЧгБЯгГЦгГ©гГЉгГЮгВ∞гГЧгВњгБЃеЕђеЉПгБЃдЄАиИђеМЦгБІгБВгВКгАБдїїжДПгБЃеЫЫиІТ嚥гБЂгБ§гБДгБ¶жИРгВКзЂЛгБ§гАВеРНеЙНгБЃзФ±жЭ•гБѓгГЙгВ§гГДгБЃжХ∞е≠¶иАЕгВЂгГЉгГЂгГїгВҐгГ≥гГИгГ≥гГїгГЦгГђгГЉгГИгВЈгГ•гГКгВ§гГАгГЉпЉИ1808вАУ1878пЉЙгБЂгБ°гБ™гВАгАВ
и®ЉжШО
еЫЫиІТ嚥гБЃйЭҐз©НгВТ S гБ®гБЩгВЛгБ®гАБ
 (¬±гБѓгАБеЗЄеЫЫиІТ嚥гБ®еЗєеЫЫиІТ嚥гБЃе†іеРИгВТзЬБзХ•гБЧгБЊгБЩ)
(¬±гБѓгАБеЗЄеЫЫиІТ嚥гБ®еЗєеЫЫиІТ嚥гБЃе†іеРИгВТзЬБзХ•гБЧгБЊгБЩ)
гВИгВК

гВТеЊЧгВЛгАВгБЊгБЯгАБдљЩеЉ¶еЃЪзРЖгВИгВКгАБ

гБІгБВгВЛгБЛгВЙ

гВТеЊЧгВЛгАВ4S2 гБЂгБ§гБДгБ¶гБЃеЉПгБ®иЊЇгАЕгВТиґ≥гБЧеРИгВПгБЫгАБеК†ж≥ХеЃЪзРЖ cos(A + C) = cos A cos C вИТ sin A sin C гВТзФ®гБДгВЛгБ®гАБ

гБ®гБ™гВЛгАВеАНиІТгБЃеЕђеЉП  гВТзФ®гБДгБ¶е§Й嚥гБЩгВЛгБ®гАБ
гВТзФ®гБДгБ¶е§Й嚥гБЩгВЛгБ®гАБ

гБ®гБ™гВЛгАВгБУгБЃеЉПгБѓгАБеНКеС®йХЈ

гВТзФ®гБДгБ¶

гБ®гБ™гВКгАБгГЦгГђгГЉгГИгВЈгГ•гГКгВ§гГАгГЉгБЃеЕђеЉПгВТеЊЧгВЛгАВ
йЦҐйА£гБЩгВЛеЕђеЉП
еЖЖгБЂеЖЕжО•гБЩгВЛеЫЫиІТ嚥гБЂгБ§гБДгБ¶гБѓгАБеѓЊиІТгБЃеТМгБЃеНКеИЖгБМ 90¬∞гБІгБВгВЛгБУгБ®гБЛгВЙгАБгГЦгГ©гГЉгГЮгВ∞гГЧгВњгБЃеЕђеЉП
- S = вИЪ(T вИТ p)(T вИТ q)(T вИТ r)(T вИТ s)
гБМжИРгВКзЂЛгБ§гАВгБЊгБЯгАБеЖЖгБЂе§ЦжО•гБЩгВЛеЫЫиІТ嚥гБЂгБ§гБДгБ¶гБѓгАБеѓЊиЊЇгБЃеТМгБМз≠ЙгБЧгБПгАБT = p + r = q + s гБІгБВгВЛгБУгБ®гБЛгВЙ

гБМжИРгВКзЂЛгБ§гАВгБХгВЙгБЂе§ЦжО•еЖЖгБ®еЖЕжО•еЖЖгВТжМБгБ§еЫЫиІТ嚥гАБгБ§гБЊгВКеПМењГеЫЫиІТ嚥гБЂгБ§гБДгБ¶гБѓгАБ
- S = вИЪpqrs
гБ®гБ™гВЛгАВгБЊгБЯгАБдЄКи®ШгБЃи®ЉжШОгБѓ p = 0 гБ®гБЧгБ¶дЄЙиІТ嚥гБЃйЭҐз©НгВТиАГгБИгБ¶гБДгВЛгБ®гБЧгБ¶гВВйАЪзФ®гБЧгАБгГШгГ≠гГ≥гБЃеЕђеЉП
- S = вИЪT(T вИТ q)(T вИТ r)(T вИТ s)
гВТеЊЧгВЛгАВ
иДЪж≥®
еПВиАГжЦЗзМЃ
йЦҐйА£й†ЕзЫЃ
е§ЦйГ®гГ™гГ≥гВѓ


























