сЃЎсЃЃсЃЂТЋ░
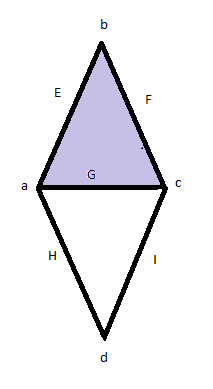
С╗БТЋ░уџёСйЇуЏИт╣ЙСйЋтГдсЂФсЂісЂёсЂдсђЂсЃЎсЃЃсЃЂТЋ░ (сЃЎсЃЃсЃЂсЂЎсЂєсђЂУІ▒Уфъ: Betti numbers) сЂ»сђЂСйЇуЏИуЕ║жќЊсЂФт»ЙсЂЎсѓІСИЇтцЅжЄЈсЂДсЂѓсѓісђЂУЄфуёХТЋ░сЂФтђцсѓњсѓѓсЂцсђѓ  тЈ│сЂ«тЏ│сЂ«сѓѕсЂєсЂфсЃѕсЃ╝сЃЕсѓ╣сѓњУђЃсЂѕсѓІсђѓсЂЊсЂ«сЃѕсЃ╝сЃЕсѓ╣сЂФтѕЄсѓітЈБсЂїтєєтЉесЂФсЂфсѓІсѓѕсЂєсЂФтѕЄсѓїУЙ╝сЂ┐сѓњсЂёсѓїсЂЪсЂесЂЇсђЂсЂЮсЂ«ухљТъюС║їсЂцсЂ«сЃћсЃ╝сѓ╣сЂФтѕєсЂІсѓїсЂфсЂётѕЄсѓіТќ╣сЂїсђЂуЕ┤сЂ«сЂЙсѓЈсѓісЂФсЂЮсЂБсЂдСИђтЉесЂЎсѓІТќ╣Т│ЋсЂесђЂуИдсЂФтѕЄТќГсЂЎсѓІТќ╣Т│ЋсЂ«С║їжђџсѓісЂѓсѓІсђѓсЂЊсЂ«сЂЊсЂесЂІсѓЅсЃѕсЃ╝сЃЕсѓ╣сЂ« 1 ТгАсЃЎсЃЃсЃЂТЋ░сЂ» 2 сЂДсЂѓсѓІ[1]сђѓуЏ┤ТёЪуџёсЂфУеђУЉЅсѓњСй┐сЂєсЂесђЂ 1 ТгАС╗ЦСИісЂ«сЃЎсЃЃсЃЂТЋ░сЂ»ТДўсђЁсЂфТгАтЁЃсЂ«ТюгУ│фуџёсЂф№йбуЕ┤№йБ№╝ѕжќЅТЏ▓уиџсђЂжќЅТЏ▓жЮбсЃ╗сЃ╗№╝ЅсЂ«ТЋ░сЂДсЂѓсѓІсђѓСЙІсЂѕсЂ░сђЂтєєсЂ« 1 ТгАсЃЎсЃЃсЃЂТЋ░сЂ» 1сЂДсЂѓсѓісђЂСИђУѕгуџёсЂфсЃЌсЃгсЃёсѓДсЃФ(pretzel)сЂ«та┤тљѕсЂ»сђЂ1 ТгАсЃЎсЃЃсЃЂТЋ░сЂ»уЕ┤сЂ«ТЋ░сЂ« 2 тђЇсЂесЂфсѓІсђѓ сЃЎсЃЃсЃЂТЋ░сЂ»сђЂС╗іТЌЦсђЂТЋ░тГдсЂ«сЂ┐сЂфсѓЅсЂџУеѕу«ЌТЕЪуДЉтГдсѓёсЃЄсѓИсѓ┐сЃФућ╗тЃЈсЂфсЂЕсЂ«тѕєжЄјсЂДсѓѓуаћуЕХсЂЋсѓїсЂдсЂёсѓІсђѓ сђїсЃЎсЃЃсЃЂТЋ░сђЇсЂесЂёсЂєсЂЊсЂесЂ░сЂ»сђЂсѓесЃ│сЃфсѓ│сЃ╗сЃЎсЃЃсЃЂ (Enrico Betti) сЂФсЂАсЂфсЂ┐сђЂсѓбсЃ│сЃфсЃ╗сЃЮсѓбсЃ│сѓФсЃг (Henri Poincar├Е) сЂФсѓѕсѓітЉйтљЇсЂЋсѓїсЂЪсђѓ т«џуЙЕk сѓњжЮъУ▓асЂ«ТЋ┤ТЋ░ сЂесЂЌсЂдсђЂуЕ║жќЊ X сЂ« k ТгАсЃЎсЃЃсЃЂТЋ░ bk(X) сЂ»сђЂX сЂ« k ТгАсЃЏсЃбсЃГсѓИсЃ╝уЙц Hk(X) сЂ«сЃЕсЃ│сѓ»сЂесЂЌсЂдт«џуЙЕсЂЋсѓїсѓІсђѓсЃЏсЃбсЃГсѓИсЃ╝уЙцсЂ»ТюЅуљєТЋ░СйЊ Q СИісЂ«сЃЎсѓ»сЃѕсЃФуЕ║жќЊсЂесЂЎсѓІсЂЊсЂесѓѓсЂДсЂЇсѓІсЂ«сЂДсђЂHk(X; Q) сЂ«сЃЎсѓ»сЃѕсЃФуЕ║жќЊсЂ«ТгАтЁЃсЂесЂЌсЂдсЃЎсЃЃсЃЂТЋ░сѓњт«џуЙЕсЂЎсѓІсЂЊсЂесѓѓсЂДсЂЇсѓІсђѓТЎ«жЂЇС┐ѓТЋ░т«џуљєсЂ»сђЂсЂГсЂўсѓїсЂ«сЂфсЂётЇўу┤ћсЂфта┤тљѕсЂФсЂ»№╝ѕС┐ѓТЋ░сЂ«тЈќсѓіТќ╣сЂФСЙЮтГўсЂЏсЂџ№╝ЅсЂЊсѓїсѓЅсЂ«т«џуЙЕсЂїтљїсЂўсЂДсЂѓсѓІсЂЊсЂесѓњуц║сЂЌсЂдсЂёсѓІсђѓ сЂЙсЂЪсЃЎсЃЃсЃЂТЋ░сѓњС┐ѓТЋ░сЂФсѓѓсЂцтцџжаЁт╝ЈсЂесЂЌсЂдсЃЮсѓбсЃ│сѓФсЃгтцџжаЁт╝Јсѓњт«џуЙЕсЂЎсѓІсђѓсЂЎсЂфсѓЈсЂАсђЂX сЂ«сЃЮсѓбсЃ│сѓФсЃгтцџжаЁт╝Ј PX(t) сЂесЂ» b0(X)+b1(X)t+b2(X)t2+...+bn(X)tn сЂ«сЂЊсЂесЂДсЂѓсѓІсђѓ СЙІтЇўСйЊУцЄСйЊСИісЂ«тЏ│сЂ«сѓѕсЂєсЂфтЇўСйЊУцЄСйЊсЂДсЂ«сЃЎсЃЃсЃЂТЋ░сѓњУеѕу«ЌсЂЎсѓІсђѓсЂЊсѓїсЂ»0-тЇўСйЊсЂесЂЌсЂд a, b, c, d, 1-тЇўСйЊсЂесЂЌсЂд E, F, G, H, I, 2-тЇўСйЊсЂесЂЌсЂдУЅ▓сЂ«сЂцсЂёсЂЪжЃетѕє J сЂЪсЂаСИђсЂцсѓњсѓѓсЂцсѓѓсЂ«сЂДсЂѓсѓІсђѓсЂЊсЂ«тЏ│сЂ«жђБухљТѕљтѕєсЂ»сЂЪсЂаСИђсЂцсЂДсЂѓсѓісђЂ1 ТгАтЁЃсЂ«уЕ┤сЂ»УЅ▓сЂ«сЂцсЂёсЂдсЂфсЂёжЃетѕєсЂЎсЂфсѓЈсЂАжаѓуѓ╣ a, c, d сѓњсѓѓсЂцСИЅУДњтйбсЂ«жЃетѕєсЂДсЂѓсѓІсђѓсЂЙсЂЪт╣│жЮбСИісЂФсЂѓсѓісђЂсђїуЕ║Т┤ъсђЇсѓњсѓѓсЂЪсЂфсЂёсђѓС╗ЦСИісЂ«С║ІсЂІсѓЅb0=1, b1=1,b2=0 сЂДсЂѓсѓісђЂсЃЮсѓбсЃ│сѓФсЃгтцџжаЁт╝ЈсЂ» 1+t сЂесЂфсѓІсђѓ сѓ░сЃЕсЃЋуљєУФќСйЇуЏИуџёсѓ░сЃЕсЃЋуљєУФќсЂДсЂ»сђЂжаѓуѓ╣ n тђІсђЂm ТюгсЂ«УЙ║сђЂk тђІсЂ«жђБухљТѕљтѕєсѓњсѓѓсЂБсЂЪсѓ░сЃЕсЃЋ G сЂ« 1ТгАсЃЎсЃЃсЃЂТЋ░сЂ»сђЂm Рѕњ n + k сЂФуГЅсЂЌсЂёсђѓ сЂЊсЂ«сЂЊсЂесЂ»сђЂУЙ║сЂ«ТЋ░сЂФсЂцсЂёсЂдсЂ«ТЋ░тГдуџётИ░у┤ЇТ│ЋсЂФсѓѕсѓіуЏ┤ТјЦУе╝ТўјсЂїсЂДсЂЇсѓІсђѓсЂцсЂЙсѓісђЂТќ░сЂЌсЂёУЙ║ 1-сѓхсѓцсѓ»сЃФтѕєсЂ«ТЋ░сѓњтбЌсѓёсЂЎсЂІсђЂсѓѓсЂЌсЂЈсЂ»УЙ║сЂ«жђБухљТѕљтѕєсЂ«ТЋ░сѓњСИђсЂцТИЏсѓЅсЂЎсЂІсЂ«сЂЕсЂАсѓЅсЂІсЂДсЂѓсѓІсђѓ уггСИђсЃЎсЃЃсЃЂТЋ░сЂ»сђЂсѓ░сѓ╣сѓ┐сЃЋсЃ╗сѓГсЃФсЃњсЃЏсЃЋ(Gustav Kirchhoff)сЂїсЃЎсЃЃсЃЂ(Betti)сЂ«УФќТќЄС╗ЦтЅЇсЂФт░јтЁЦсЂЌсЂЪућеУфъсЂДсЂѓсѓІсѓхсѓцсѓ»сЃГсЃъсЃЂсЃЃсѓ»ТЋ░(cyclomatic number)сЂесѓѓтЉ╝сЂ░сѓїсѓІсђѓ[2]уггСИђсЃЎсЃЃсЃЂТЋ░сЂ«сѓйсЃЋсЃѕсѓдсѓДсѓбтиЦтГдсЂИсЂ«т┐юућесЂ»сђЂтЙфуњ░уџёУцЄжЏЉт║дсѓњтЈѓуЁДсЂ«сЂЊсЂесђѓ сѓ░сЃЕсЃЋсЂ«угг 0 уЋфсѓЂсЂ«сЃЎсЃЃсЃЂТЋ░сЂ»сђЂжђБухљТѕљтѕєсЂ«ТЋ░ k сѓњтЇўу┤ћсЂФТёЈтЉ│сЂЌсЂдсЂёсѓІсђѓ[3] сЃЮсѓбсЃ│сѓФсЃгтцџжаЁт╝ЈсЂ«Уеѕу«ЌСЙІ
уёАжЎљТгАтЁЃсЂ«УцЄу┤ат░ётй▒уЕ║жќЊсЂ«сЃЎсЃЃсЃЂТЋ░сЂ«тѕЌсЂ»сђЂ1, 0, 1, 0, 1, ... сЂетЉеТюЪуџёсЂесЂфсѓІсЂ«сЂДсђЂтЉеТюЪсЂ«жЋисЂЋсЂ» 2 сЂДсЂѓсѓІсђѓсЂЊсЂ«та┤тљѕсЂ»сђЂсЃЮсѓбсЃ│сѓФсЃгтЄйТЋ░сЂ»тцџжаЁт╝ЈсЂДсЂ»сЂфсЂЈсђЂуёАжЎљу┤џТЋ░ сЂесЂфсѓІсђѓсЂЊсѓїсЂ»сђЂт╣ЙСйЋу┤џТЋ░сЂДсЂѓсѓісђЂТгАсЂ«ТюЅуљєтЄйТЋ░сЂесЂЌсЂдТЏИсЂЇУАесЂЎсЂЊсЂесЂїсЂДсЂЇсѓІсђѓ сѓ│сЃ│сЃЉсѓ»сЃѕсЂфтЇўу┤ћсЃфсЃ╝уЙцсЂ«сЃЮсѓбсЃ│сѓФсЃгтцџжаЁт╝ЈсЂ»сђЂ сЂесЂфсѓІсђѓ ТђДУ│ф№╝ѕТюЅуљє№╝ЅсЃЎсЃЃсЃЂТЋ░ bk(X) сЂ»сђЂсЃЏсЃбсЃГсѓИсЃ╝уЙцсЂ«С╗╗ТёЈсЂ«сЂГсЂўсѓїжЃетѕєуЙц(torsion)сѓњУђЃТЁ«сЂФтЁЦсѓїсЂдсЂ»сЂёсЂфсЂёсЂїсђЂсЂЌсЂІсЂЌсђЂжЮътИИсЂФтЪ║ТюгуџёсЂфСйЇуЏИСИЇтцЅжЄЈсЂДсЂѓсѓІсђѓ ТюЅжЎљсЂ«тЇўСйЊУцЄСйЊсЂ«та┤тљѕсЂ»сђЂсЃЏсЃбсЃГсѓИсЃ╝уЙц Hk(X, Z) сЂ»тЁесЂдсЂ« k сЂДТюЅжЎљсЃЕсЃ│сѓ»сЂДсЂѓсѓісђЂсЂЙсЂЪ k сЂїтЇўСйЊсЂ«ТгАтЁЃсѓњУХЁсЂѕсЂдсЂёсѓІта┤тљѕсЂ» 0 сЂДсЂѓсѓІсђѓ ТюЅжЎљсЂ« CW-УцЄСйЊ K сЂФт»ЙсЂЌсђЂ сЂїТѕљсѓіуФІсЂцсђѓсЂЊсЂЊсЂФ сЂ» K сЂ«сѓфсѓцсЃЕсЃ╝ТеЎТЋ░сѓњУАесЂЌсђЂF сЂ»С╗╗ТёЈсЂ«СйЊсЂДсЂѓсѓІсђѓ 2сЂцсЂ«уЕ║жќЊ X сЂе Y сЂФт»ЙсЂЌ сЂїТѕљсѓіуФІсЂцсђѓсЂЊсЂЊсЂФ PX сЂ» X сЂ« сЃЮсѓбсЃ│сѓФсЃгтцџжаЁт╝Ј(Poincar├Е polynomial)№╝ѕсѓѕсѓіСИђУѕгуџёсЂФсЂ»сђЂуёАжЎљТгАтЁЃсЂ«уЕ║жќЊсЂФт»ЙсЂЌсЂдсЂ»сЃЮсЃ»сЃ│сѓФсЃгтцџжаЁт╝Ј№╝ЅсђЂсЂЎсЂфсѓЈсЂА X сЂ«сЃЎсЃЃсЃЂТЋ░сЂ«Т»ЇтЄйТЋ░сЂДсЂѓсѓІ сЂДсЂѓсѓІсђѓсѓГсЃЇсЃЃсЃѕсЂ«т«џуљє(K├╝nneth theorem)сѓњтЈѓуЁДсђѓ X сѓњтљЉсЂЇС╗ўсЂЉтЈ»УЃйсЂфжќЅтцџТДўСйЊсЂД n ТгАтЁЃсЂесЂЎсѓІсЂесђЂС╗╗ТёЈсЂ« k сЂФт»ЙсЂЌ k сЂе n − k сѓњтЁЦсѓїТЏ┐сЂѕсѓІсЃЮсѓбсЃ│сѓФсЃгтЈїт»ЙТђД сЂїсЂѓсѓІсђѓ сЃЏсЃбсЃГсѓИсЃ╝уЙцсЂїТЇЕсѓїсѓњТїЂсЂЪсЂфсЂёсЂесЂЇсђЂсЃЎсЃЃсЃЂТЋ░сЂ»С┐ѓТЋ░СйЊ F сЂФсѓѕсѓЅсЂџТ▒║сЂЙсѓІсђѓу┤аТЋ░ p сЂФт»ЙсЂЌТЋ┤ТЋ░С┐ѓТЋ░сЃЏсЃбсЃГсѓИсЃ╝уЙцсЂ« p-torsion сЂ»ТеЎТЋ░ p сѓњсѓѓсЂцС┐ѓТЋ░СйЊ F сЂ«сЃЎсЃЃсЃЂТЋ░ bi(X,F) сѓњућесЂёсЂд№╝ѕтЇўу┤ћсЂфта┤тљѕсЂФсЂ»сђЂTorтЄйТЅІсѓњтЪ║уцјсЂесЂЎсѓІ№╝ЅТЎ«жЂЇС┐ѓТЋ░т«џуљєсЂФсѓѕсѓіУЕ│у┤░сЂФТ▒ѓсѓЂсѓЅсѓїсѓІсђѓ тЙ«тѕєтйбт╝ЈсЂ«уЕ║жќЊсЂ«ТгАтЁЃсЂесЂ«жќбС┐ѓX сЂїжќЅтцџТДўСйЊсЂ«сЂесЂЇсђЂсЃЎсЃЃсЃЂТЋ░сЂ»сЃЅсЃ╗сЃЕсЃ╝сЃасѓ│сЃЏсЃбсЃГсѓИсЃ╝сЂ«ТгАтЁЃсѓњсЂѓсЂЪсЂѕсѓІсђѓжќЅтйбт╝ЈсЂ«уЕ║жќЊсѓњт«їтЁетйбт╝ЈсЂ«уЕ║жќЊсЂДсѓЈсЂБсЂЪтЋєуЕ║жќЊсЂ«ТгАтЁЃсѓњсЂѓсЂЪсЂѕсѓІсђѓсЂЊсѓїсЂ»сЃЅсЃ╗сЃЕсЃ╝сЃасЂ«т«џуљєсЂесЃЏсЃбсЃГсѓИсЃ╝УФќсЂ«ТЎ«жЂЇС┐ѓТЋ░т«џуљєсЂФсѓѕсѓісЂѕсѓЅсѓїсѓІсђѓ сЂЙсЂЪ X сЂїсЃфсЃ╝сЃъсЃ│тцџТДўСйЊсЂДсЂѓсѓїсЂ░сђЂсЃЏсЃЃсѓИуљєУФќсЂФсѓѕсѓїсЂ░сЃЎсЃЃсЃЂТЋ░сЂ»Уф┐тњїтйбт╝ЈсЂ«уЕ║жќЊсЂ«ТгАТЋ░сѓњСИјсЂѕсѓІсЂЊсЂесЂїсѓЈсЂІсѓІсђѓ сЃбсЃ╝сѓ╣уљєУФќсЂФсѓѕсѓісЃЎсЃЃсЃЂТЋ░сЂ«С║цС╗БтњїсЂесђЂт»Йт┐юсЂЎсѓІжЂЕтѕЄсЂфсЃбсЃ╝сѓ╣тЄйТЋ░сЂ«УЄеуЋїуѓ╣сЂ«ТЋ░ Ni сЂ«С║цС╗БтњїсЂФжќбсЂЎсѓІСИЇуГЅт╝ЈсЂїС╗ЦСИІсЂ«сѓѕсЂєсЂФсЂѓсЂЪсЂѕсѓЅсѓїсѓІсђѓ сѓдсѓБсЃЃсЃєсЃ│сЂ»сђЂсЃбсЃ╝сѓ╣тЄйТЋ░сѓњСй┐сЂёсЂЊсѓїсѓЅсЂ«СИЇуГЅт╝ЈсЂ«УфгТўјсѓњсЂЌсЂдсђЂсЃЅсЃ╗сЃЕсЃ╝сЃаУцЄСйЊсЂ«тцќтЙ«тѕєсѓњтцЅтйбсЂЌсЂЪсђѓ[4] тЈѓУђЃТќЄуї«
|
Portal di Ensiklopedia Dunia