Х╥ЁЦ│╜Ц┌▀Ц┐°Ц┐╪Ц┐╚Ц─┌Г╘╨Ф╟≈Ф┼╣Ф┼≈ Ц│╝Е╫╠И÷©Ц┌▓Е▐≈Ц│▒Ц┌▀Ц│÷Ц┌│Ц─│И│▀Е▀∙Ц│╞Е╝▄Е┘╗Ц│╚Ф■╬Г┴╘Г╥ Ц┌▓Ф▐▐Ц│▐Ц┌▐Ц│▒Ц│╖Ц│╞Ц│╙Ц│└Ц─┌ Ц┐°Ц┐╪Ц┐╚Ц│╝Х╥ЁЦ│╜Х©■Ц┌┼И│▀Е▀∙ О╪┬Ц┐°Ц┐╪Ц┐╚Ц│╝Ц│╞Ц│╜Ц│▀Ц│┬Ц┌┼Ц│├Ц┌⌠Ц│╘Ц│├О╪┴Ц│╗Ц│╞Ц─│Д╩√Ц│╝Г┴╘Д╫⌠Ц│╚Х║²Г╙│Ц│≈Ц│╕Х╥ЁЦ│╜Х©■Ц┌▀Ц┐°Ц┐╪Ц┐╚ Ц│╝Г┴╘Г░├Г └Ц│╙Ф▄╞Ц┌▀Х┬·Ц│└Ц│╝Ц│⌠Ц│╗Ц│╖Ц│┌Ц┌▀Ц─┌Г┴╧Ц│╚Д╩√Ц│╝Г┴╘Д╫⌠ Х║╗И²╒Ц│╗Х║²Г╙│ Ц│≥Ц┌▀Г⌡╢Е┴█Ц─│Г·╛И√⌠Ц─│Г⌡╢Е╬▄Ц│╝И│▀Е▀∙ Ц│╚Ц│╓Ц│└Ц│╕Ф╕┌Х╙╛Ц│≥Ц┌▀Ц─┌Х╥ЁЦ│╜Х©■Ц┌▀Ц┐°Ц┐╪Ц┐╚Ц│╝Ф▄╞Ц┌▀Х┬·Ц│└Ц│╝Д╦─И┐╗Ц│╞Ц─│И╚≤Ф═║ Ц│╬Ц│÷Ц│╞Е╜╕И┐╗ Ц┐╛Ц┐≥Ц┐╚Ц│╝Г┴╘Г░├Е╜╕Ц│╚Ц│┼Ц│└Ц│╕Ц─│Е┼⌡Е╜╕ Ц│╝Е╟▌Е┘╔Ц│╗Ц│≈Ц│╕Е╫╧Г╚▀Ц│╓Ц┌┬Ц│├Ц│╙И║▄Ф²░Ц│╖Ц│┌Ц┌▀[ 1] Ц┌╧Ц┐²Ц┐╪Ц┐└Е╥╔Е╜╕ О╪┬Х▀╠Х╙·Г┴┬ О╪┴
Ц┐°Ц┐╪Ц┐╚Ц│╝Ц│╣Ц┌▀Ц│╬Ц│└Ц│╞Д╦─Х┬╛Ц│╚Ф√°Ф√╧Ф┼∙Е╟└ О╪┬И┤█Е┼⌡ Ц─│Ф┼≈Е┼⌡ Ц─│Ц┐·Ц┌╟Ц┐▄Ц┌╧Е┼╧Ф·° Ц─│Ф╣╝Е┼⌡ Ц│╝Е╫╠И÷©Ц┌▓Е▐≈Ц│▒Ц┌▀О╪┴Ц│╗Ц│≈Ц│╕Ф┴╠Ц│├Ц│⌠Ц│╗Ц│▄Ц│╖Ц│█Ц┌▀Ц│▄Ц─│Г┴╧Ц│╚Д╩√Г┴╘Д╫⌠Ц│╗Ц│╝Х║²Г╙│Ц│╞Ц─│И─ Е╦╦Е▐█Г≥╨Д©┌Ф∙╟ Ц│╚Ц┌┬Ц│ёЦ│╕Г┴╧Е╬╢Ц│╔Ц│▒Ц┌┴Ц┌▄Ц┌▀О╪┬Ц┐°Ц┐╪Ц┐╚Ц│²Ц│╝Ц┌┌Ц│╝Ц┌└Х║²Г╙│И²╒Ц│╝Ф─╖ХЁ╙Ц─│Х║²Г╙│И─÷Е╨╕ Ц─│Е⌡·Х╩╒ Ц─│Ф╦╘Е╨╕ Ц┌└Е°╖Е┼⌡ Ц│╙Ц│╘Ц│╝Е╠─Ф┴─Г └Ц│╙Ф²║Д╩╤Ц│╚Ц┌┬Ц│ёЦ│╕Е╓┴Е▄√Ц│≥Ц┌▀О╪┴Ц─┌Е╓ Ц│▐Ц│╝Ц┌╧Ц┐²Ц┐╪Ц┐└ Г╚╤Ф┼─Ц│╚Ц│┼Ц│└Ц│╕Ц│╞Ц─│Ц┐∙Ц┌╖Ц┌╒Ц┐≈Ц┐╛Ц┐╪ Ц┌▓Ф▀┘Д©²Ц│≥Ц┌▀Ц│÷Ц┌│Ц│╚Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╝Е╪╬Ф─╖ Ц│╚Д╦─Е╝ Ц│╝Е┬╤И≥░Ц┌▓Х╙╡Ц│≈Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╝Г╘╨Е┼⌡ Г └Ц│╙Г┴╧Ф─╖Ц┌▓Д╦█Ф╜ёЦ│╚Е╓┴Е▄√Ц│∙Ц│⌡Ц┌▀Ц│⌠Ц│╗Ц┌▓Г╕│Ц│≤Ц│╕Ц│└Ц┌▀Ц─┌Ц┐°Ц┐╪Ц┐╚Ц│╝Е╪╬Ф─╖Ц│╞Ц─│Ц┐║Ц┌╫Ц┌╒Ц┐║Ц┐╙Ц┌╚Ц│╝Г░┐Ф┬╞ Ц│▄Х║▄Ц┌▐Ц┌▄Ц│╕Ц│└Ц│÷Ц┌┬Ц│├Ц│╙Е▐╓Ц│└Ф≥┌Ф°÷Ц│▀Ц┌┴Ц┌╧Ц┐²Ц┐╪Ц┐└Ц│╝Г┴╧Е╬╢Ц│╝Д╦─Ц│╓Ц│╚Ц│╙Ц│ёЦ│╕Ц│└Ц│÷[ 2]
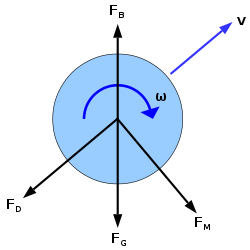
Г╘╨Д╦╜Ц┌▓Е⌡·Х╩╒Ц│≈Ц│╙Ц│▄Ц┌┴Иё⌡Ц│╤Ц┐°Ц┐╪Ц┐╚Ц│╚Д╫°Г■╗Ц│≥Ц┌▀Е┼⌡ Ц─┌И┤█Е┼⌡ О╪┬F G О╪┴Ц─│Ф┼≈Е┼⌡ О╪┬F D О╪┴Ц─│Ц┐·Ц┌╟Ц┐▄Ц┌╧Е┼⌡ О╪┬F M О╪┴Ц─│Ф╣╝Е┼⌡ О╪┬F B О╪┴Ц─┌ Ц┐░Ц┌╕Ц┐ЁЦ┐┴Ц│≥Ц┌▀Ц┐°Ц┐╪Ц┐╚Ц│╝И│▀Е▀∙Ц│╞Ц─│Ф┼∙Е╟└ И│▀Е▀∙Ц│╚Е╬⌠Ц│├[ 3] [ 4] Е┼⌡ Ц│▄Д╫°Г■╗Ц│≈Ц│╕Ц│└Ц┌▀Ц─┌Д╩ёХ║╗Г └Ц│╙Ц┌┌Ц│╝Ц│╗Ц│≈Ц│╕Ц│╞Ц─│И┤█Е┼⌡ О╪┬F G О╪┴Ц─│Г╘╨Ф╟≈Ф┼╣Ф┼≈Ц│╚Ц┌┬Ц┌▀Ф┼≈Е┼⌡ О╪┬F D О╪┴Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╝Ц┌╧Ц┐■Ц┐Ё Ц│╚Ц┌┬Ц┌▀Ц┐·Ц┌╟Ц┐▄Ц┌╧Е┼⌡ О╪┬F M О╪┴Ц─│Ф╣╝Е┼⌡ О╪┬F B О╪┴Ц│╙Ц│╘Ц│▄Ц│┌Ц┌▀[ 5] И│▀Е▀∙Ф√╧Г╗▀Е╪▐ Ц┌▓Г■╗Ц│└Ц┌▄Ц│╟Ц┌┬Ц│└Ц─┌Ц│╙Ц│┼Ц─│Д╩╔Д╦▀Ц│╖Ц│╞И²╒Ц│╚Е╞╬Ц│≈Ц│╕Ф╟╢Е╧ЁЦ│╖Ц┐°Ц┐╪Ц┐╚Ц│╝И─╡Х║▄Ф√╧Е░▒Ц│╗Е░▄Ц│≤Е░▒Ц│█Ц┌▓x Х╩╦Ц─│И²╒Ц│╚Е╞╬Ц│≈Ц│╕Е·┌Г⌡╢Ц│╙Ф√╧Е░▒Ц┌▓y Х╩╦Ц─│И²╒Ц│╚Е╞╬Ц│≈Ц│╕Ф╟╢Е╧ЁЦ│╖Ц┐°Ц┐╪Ц┐╚Ц│╝И─╡Х║▄Ф√╧Е░▒Ц│╚Г⌡╢Д╨╓Ц│≥Ц┌▀Е░▒Ц│█Ц┌▓z Х╩╦Ц│╗Ц│≥Ц┌▀Ц─┌Ц│╬Ц│÷Ц│²Ц┌▄Ц│·Ц┌▄Ц│╝Х╩╦Ц│╝Е█≤Д╫█Ф√╧Е░▒Ц┐≥Ц┌╞Ц┐┬Ц┐╚Ц┌▓Ц│²Ц┌▄Ц│·Ц┌▄i , j , k Ц│╗Х║╗Ц│≥Ц─┌
Б┬▒
F
=
m
a
F
G
+
F
D
+
F
M
+
F
B
=
m
a
=
m
d
v
d
t
=
m
d
2
r
d
t
2
{\displaystyle {\begin{aligned}\sum \mathbf {F} &=m\mathbf {a} \\\mathbf {F} _{\text{G}}+\mathbf {F} _{\text{D}}+\mathbf {F} _{\text{M}}+\mathbf {F} _{\text{B}}&=m\mathbf {a} =m{\frac {d\mathbf {v} }{dt}}=m{\frac {d^{2}\mathbf {r} }{dt^{2}}}\end{aligned}}}
Ц│⌠Ц│⌠Ц│╖Ц─│m Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│╝ХЁ╙И┤▐Ц│╖Ц│┌Ц┌▀Ц─┌Ц│╬Ц│÷Ц─│a Ц─│v Ц─│r Ц│╞Ц│²Ц┌▄Ц│·Ц┌▄Ц─│Ф≥┌И√⌠ t Ц│╚Ц│┼Ц│▒Ц┌▀Ц┐°Ц┐╪Ц┐╚Ц│╝Е┼═И─÷Е╨╕ Ц─│И─÷Е╨╕ Ц─│Д╫█Г╫╝ Ц┌▓Х║╗Ц│≥Ц─┌
Е°╟И²╒Ц│╚Х║²Г╙│Е╬▄Ц─│Д╩╟Х╖▓70б╟Ц│╖Х╥ЁЦ│╜Д╦┼Ц│▄Ц│ёЦ│÷Ц┐°Ц┐╪Ц┐╚Ц│▄Е├█Ц│ЁЕ°╟И²╒Ц│╚Е┬╟И│■Ц│≥Ц┌▀Ц│╬Ц│╖Ц│╝Е╪╬И│⌠Ц─┌ :Ф┼╣Ф┼≈Ц┌▓Х─┐Ц│┬Ц│╙Ц│└Е═╢Е░┬Ц─┌ :Ц┐╛Ц┌╓Ц┐▌Ц┐╚Ц┌╨Ф∙╟Ц│▄Е╟▐Ц│∙Ц│▐Ц┌╧Ц┐┬Ц┐╪Ц┌╞Ц┌╧Ц│╝ФЁ∙Е┴┤ Ц│╚Ц│≈Ц│÷Ц│▄Ц│├Г╘╨Ф╟≈Ф┼╣Ф┼≈Ц┌▓Х─┐Ц│┬Ц┌▀Е═╢Е░┬Ц─┌ :Ц┐╛Ц┌╓Ц┐▌Ц┐╚Ц┌╨Ф∙╟Ц│▄Е╓╖Ц│█Ц│▐Ц┐▀Ц┐╔Ц┐╪Ц┐┬Ц┐ЁЦ│╝Ф┼╣Ф┼≈ФЁ∙Е┴┤ Ц│╚Ц│≈Ц│÷Ц│▄Ц│├Ф┼╣Ф┼≈Ц┌▓Х─┐Ц│┬Ц┌▀Е═╢Е░┬Ц─┌ И┤█Е┼⌡ Ц│╞Г┴╘Д╫⌠Ц│╚Е╞╬Ц│≈Ц│╕И┴⌡Г⌡╢ Д╦▀Е░▒Ц│█Ц│╚Е┐█Ц│█Ц─│Ц│²Ц│╝Е╓╖Ц│█Ц│∙Ц│╞Д╩╔Д╦▀Ц│╝Г╜┴Е╪▐Ц│╖Х║╗Ц│⌡Ц┌▀[ 6]
F
G
=
m
g
{\displaystyle F_{\text{G}}=mg}
Ц│⌠Ц│⌠Ц│╖m Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│╝ХЁ╙И┤▐Ц─│g Ц│╞И┤█Е┼⌡Е┼═И─÷Е╨╕ Ц│╖Ц│┌Ц┌┼Ц─│Е°╟Г░┐ Д╦┼Ц│╖Ц│╞m/s2 2 [ 7] [ ФЁ╗И┤┬ 1] Г░├Ф┐ЁГ └Ц│╙Ф²║Д╩╤ О╪┬Х▀╠Х╙·Г┴┬ О╪┴ Е┼⌡Е╜╕Г └Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪ Ц│▄Д©²Е╜≤ Ц│∙Ц┌▄Ц┌▀[ 11] [ 12]
a
=
Б┬▓
g
j
v
=
v
0
+
a
t
r
=
r
0
+
v
0
t
+
1
2
a
t
2
{\displaystyle {\begin{aligned}\mathbf {a} &=-g\mathbf {j} \\\mathbf {v} &=\mathbf {v} _{\text{0}}+\mathbf {a} t\\\mathbf {r} &=\mathbf {r} _{0}+\mathbf {v} _{0}t+{\frac {1}{2}}\mathbf {a} t^{2}\end{aligned}}}
Ц│⌠Ц│⌠Ц│╖a Ц─│v Ц─│r Ц│╞Ц│²Ц┌▄Ц│·Ц┌▄Ц─│Ф≥┌И√⌠tЦ│╚Ц│┼Ц│▒Ц┌▀ Ц┐°Ц┐╪Ц┐╚Ц│╝Е┼═И─÷Е╨╕Ц─│И─÷Е╨╕Ц─│Д╫█Г╫╝Ц┌▓Х║╗Ц│≈Ц─│v0 Ц─│r0 Ц│╞Ц│²Ц┌▄Ц│·Ц┌▄Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╝Е┬²И─÷Е╨╕Ц│┼Ц┌┬Ц│ЁЕ┬²Ф°÷Д╫█Г╫╝Ц┌▓Х║╗Ц│≥Ц─┌
Ц┌┬Ц┌┼Е┘╥Д╫⌠Г └Ц│╙Д╬▀Ц┌▓Х╖ёФ·░Ц│≥Ц┌▀Ц─┌Ц┐°Ц┐╪Ц┐╚Ц│▄Е°╟И²╒Ц│╚Ф▌╔Х╖╕Ц│≈Ц│╕Ц┐░Ц┌╕Ц┐ЁЦ┐┴Ц│≈Ц─│Е°╟И²╒Ц│╚Е╞╬Ц│≈Ц│╕Х╖▓Е╨╕н╦ Ц│╝Е░▒Ц│█Ц│╚И│▀Е▀∙Ц│≥Ц┌▀Ц│╗Ц│█Ц─│Ц│²Ц│╝И│▀Е▀∙Ц│╝x Х╩╦Ф√╧Е░▒Ф┬░Е┬├Ц│╗y Х╩╦Ф√╧Е░▒Ф┬░Е┬├О╪┬Ц│²Ц┌▄Ц│·Ц┌▄Ф╟╢Е╧ЁФ√╧Е░▒Ц│╗Е·┌Г⌡╢Ф√╧Е░▒Ц│╝Е▀∙Ц│█Ц┌▓Х║╗Ц│≥О╪┴Ц│╞Ф╛║Ц│╝Ц┌┬Ц│├Ц│╚Х║╗Ц│⌡Ц┌▀[ 13]
x Х╩╦Ф┬░Е┬├
a
x
=
0
v
x
=
v
0
cos
Б│║
(
н╦
)
x
=
x
0
+
v
0
cos
Б│║
(
н╦
)
t
{\displaystyle {\begin{aligned}a_{x}&=0\\v_{x}&=v_{0}\cos \left(\theta \right)\\x&=x_{0}+v_{0}\cos \left(\theta \right)t\end{aligned}}}
y Х╩╦Ф┬░Е┬├
a
y
=
Б┬▓
g
v
y
=
v
0
sin
Б│║
(
н╦
)
Б┬▓
g
t
y
=
y
0
+
v
0
sin
Б│║
(
н╦
)
t
Б┬▓
1
2
g
t
2
{\displaystyle {\begin{aligned}a_{y}&=-g\\v_{y}&=v_{0}\sin \left(\theta \right)-gt\\y&=y_{0}+v_{0}\sin \left(\theta \right)t-{\frac {1}{2}}gt^{2}\end{aligned}}}
Ц│⌠Ц│╝Ф√╧Г╗▀Е╪▐Ц│▀Ц┌┴Ц│╞Ц─│Е╧ЁЦ┌┴Ц│╙И²╒Ц│╚Х║²Г╙│Ц│≈Ц│╕Х╥ЁЦ│╜Х©■Ц│ёЦ│÷Ц┐°Ц┐╪Ц┐╚Ц│▄Е┬╟И│■Ц│≥Ц┌▀Ф°─Е╓╖Ц│╝И╚≤Е╨╕О╪┬H О╪┴Ц│╗Иё⌡Х╥²И⌡╒О╪┬R О╪┴Ц│┼Ц┌┬Ц│ЁФ╛║Ц│╚Е°╟И²╒Ц│╚Х║²Г╙│Ц│≥Ц┌▀Ц│╬Ц│╖Ц│╝Ф≥┌И√⌠О╪┬T О╪┴[ ФЁ╗И┤┬ 2] [ 3] [ 13]
H
=
v
0
2
2
g
sin
2
Б│║
(
н╦
)
R
=
v
0
2
g
sin
Б│║
(
2
н╦
)
T
=
2
v
0
g
sin
Б│║
(
н╦
)
{\displaystyle {\begin{aligned}H&={\frac {v_{0}^{2}}{2g}}\sin ^{2}\left(\theta \right)\\R&={\frac {v_{0}^{2}}{g}}\sin \left(2\theta \right)\\T&={\frac {2v_{0}}{g}}\sin \left(\theta \right)\end{aligned}}}
Д╩╔Д╦┼Ц│╖Ц│╞И┤█Е┼⌡Ц│╝Е╫╠И÷©Ц│╝Ц│©Ц┌▓Х─┐Ф┘╝Ц│≈Ц│╕Ц┐°Ц┐╪Ц┐╚Ц│╝И│▀Е▀∙Ц┌▓Х╖ёФ·░Ц│≈Ц│÷Ц│▄Ц─│Ц│∙Ц┌┴Ц│╚Г╘╨Ф╟≈Ф┼╣Ф┼≈ О╪┬Ц│┼Ц┌┬Ц│ЁФ┼≈Е┼⌡Ц┌└И╒╗ Ц│╚И√╒И─ёЦ│≥Ц┌▀Е┼╧Ф·°О╪┴Ц─│Ц┐·Ц┌╟Ц┐▄Ц┌╧Е┼╧Ф·° Ц─│Ф╣╝Е┼⌡ Ц┌▓Х─┐Ф┘╝Ц│╚Е┘╔Ц┌▄Ц┌▀Ц│⌠Ц│╗Ц│╚Ц┌┬Ц│ёЦ│╕Ц─│Ц┌┬Ц┌┼Х╘ЁГ╢╟Ц│╚Х╖ёФ·░Ц│≥Ц┌▀Ц│⌠Ц│╗Ц│▄Ц│╖Ц│█Ц┌▀Ц─┌Ц┐°Ц┐╪Ц┐╚Ц│▄Х╩╫Ц│▒Ц┌▄Ц│╟Х╩╫Ц│└Ц│╩Ц│╘Е╝╧Ф≤⌠Ц│╚Е┼═И─÷Ц│≥Ц┌▀Ц│÷Ц┌│Ц─│Ц┐°Ц┐╪Ц┐╚Ц│▄Х╩╫Ц│└Ц│╩Ц│╘Г╘╨Ф╟≈Ф┼╣Ф┼≈Ц│╙Ц│╘Ц│╝И┤█Е┼⌡Д╩╔Е╓√Ц│╝Е┼⌡Ц│╝Е╫╠И÷©Ц┌▓Ц─│Ц┌┬Ц┌┼Е╪╥Ц│▐Е▐≈Ц│▒Ц┌▀Ц│⌠Ц│╗Ц│╚Ц│╙Ц┌▀Ц─┌
Ц┐°Ц┐╪Ц┐╚Ц│╝Е▒╗Ц┌┼Ц│╝Г╘╨Ф╟≈Ц│╝Ф╣│Ц┌▄Ц│╞Ц─│Д╩╔Д╦▀Ц│╖Е╝ Г╬╘Ц│∙Ц┌▄Ц┌▀Ц┐╛Ц┌╓Ц┐▌Ц┐╚Ц┌╨Ф∙╟ О╪┬ReО╪┴Ц│╝Е─╓Ц│╝Г╞└Е⌡╡Ц│╚Ц┌┬Ц│ёЦ│╕Ц─│Е╠╓Ф╣│ Ц│╬Ц│÷Ц│╞Д╧╠Ф╣│ Ц│╝Ц│└Ц│ Ц┌▄Ц│▀Ц│╚Е┬├И║·Ц│∙Ц┌▄Ц┌▀[ 15]
Re
=
о│
D
v
н╪
{\displaystyle {\text{Re}}={\frac {\rho Dv}{\mu }}}
Ц│⌠Ц│⌠Ц│╖Ц─│о│ Ц│╞Г╘╨Ф╟≈Е╞├Е╨╕ О╪┬Х▀╠Х╙·Г┴┬ О╪┴ н╪ Ц│╞Г╘╨Ф╟≈Ц│╝Г╡≤Ф─╖Д©┌Ф∙╟ Ц─│D Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│╝Г⌡╢Е╬└Ц─│v Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│╝Г╘╨Ф╟≈Ц│╚Е╞╬Ц│≥Ц┌▀И─÷Ц│∙Ц│╖Ц│┌Ц┌▀Ц─┌Д╬▀Ц│┬Ц│╟Г╘╨Ф╟≈Ц│╝Ф╦╘Е╨╕Ц│▄б╟C о│ = 3 н╪ = ц≈ 10Б┬▓5 Paб╥s[ 16]
Ц┐╛Ц┌╓Ц┐▌Ц┐╚Ц┌╨Ф∙╟Ц│▄И²·Е╦╦Ц│╚Е╟▐Ц│∙Ц│└Ц│╗Ц│█Ц│╚Ц│╞О╪┬Re < 1О╪┴Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╚Ц│▀Ц│▀Ц┌▀Ф┼≈Е┼⌡Ц│╝Е╓╖Ц│█Ц│∙Ц│╞Д╩╔Д╦▀Ц│╝Ц┌╧Ц┐┬Ц┐╪Ц┌╞Ц┌╧Ц│╝ФЁ∙Е┴┤ Ц│╚Ц┌┬Ц┌┼Х║╗Ц│∙Ц┌▄Ц┌▀[ 17]
F
D
=
6
о─
н╪
r
v
{\displaystyle F_{\text{D}}=6\pi \mu rv}
Ц│⌠Ц│⌠Ц│╖Ц─│r Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│╝Е█┼Е╬└Ц│╖Ц│┌Ц┌▀Ц─┌Ц│⌠Ц│╝Ф┼≈Е┼⌡Ц│╞Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╝И─╡Х║▄Ф√╧Е░▒Ц│╗Ц│╞Е▐█Е╞╬Е░▒Ц│█Ц│╚Д╫°Г■╗Ц│≥Ц┌▀О╪┬Ц│≥Ц│╙Ц┌▐Ц│║
Б┬▓
v
{\displaystyle \textstyle -\mathbf {v} }
4 Ц─°105 Ц│╝Г╞└Е⌡╡Ц│╚Ц│┼Ц│∙Ц│╬Ц┌▀Ц│⌠Ц│╗Ц│▄Е╓ Ц│▐Ц─│Ц┌╧Ц┐┬Ц┐╪Ц┌╞Ц┌╧Ц│╝ФЁ∙Е┴┤Ц┌▓И│╘Г■╗Ц│≥Ц┌▀Ц│⌠Ц│╗Ц│▄Ц│╖Ц│█Ц│╙Ц│└[ 18] Д╩╔Д╦▀Ц│╝Е╪▐ О╪┬Х▀╠Х╙·Г┴┬ О╪┴ [ 19]
F
D
=
1
2
о│
C
d
A
v
2
{\displaystyle F_{\text{D}}={\frac {1}{2}}\rho C_{\text{d}}Av^{2}}
Ц│⌠Ц│⌠Ц│╖Ц─│C d Ц│╞Ф┼≈Е┼⌡Д©┌Ф∙╟ Ц─│A Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│╝Ф√╜И²╒Г╘█ Ц│╖Ц│┌Ц┌▀Ц─┌
И─╡Х║▄Ф√╧Е░▒Ц│╗Ц│╞И─├Ц│╝Е░▒Ц│█Ц│╝Ф┼≈Е┼⌡Ц┌▓Е▐≈Ц│▒Ц┌▀Ц│⌠Ц│╗Ц│╖Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╞Иё⌡Х║▄Ц│≥Ц┌▀И√⌠Ц│╚Е┼⌡Е╜╕Г └Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪Ц┌▓Е╓╠Ц│├Ц│÷Ц┌│Ц─│И╚≤Е╨╕Ц┌└Иё⌡Х╥²И⌡╒Ц│▄Ф╦⌡Е╟▒Ц│≥Ц┌▀Ц│⌠Ц│╗Ц│╚Ц│╙Ц┌▀Ц─┌Ц│╬Ц│÷Д╩√Ф√╧Ц│╖Ц│╞Ц─│Ф╗╙И╒╗Ц│╚Ц┌┬Ц│ёЦ│╕Ц┐°Ц┐╪Ц┐╚Ц│╞Ф°╛Ф²╔Ц│╝Г╣▄Х╥╞Ц│▀Ц┌┴И─╦Х└╠Ц│≥Ц┌▀Е═╢Е░┬Ц┌┌Ц│┌Ц┌▀Ц─┌Ц┌╢Ц┐╚Ц┐∙Ц│╙Ц│╘Ц│╝Ц┐≈Ц┐╛Ц┐╪Ц┐╓Ц┐╪Ц│╞Ц─│Ц│⌠Ц│╝Д╦║Ф√╧Ц│╝Е┼╧Ф·°Ц┌▓Х─┐Ф┘╝Ц│╚Е┘╔Ц┌▄Ц┌▀Е©┘Х╕│Ц│▄Ц│┌Ц┌▀[ 20]
Ц┐░Ц┐┐Ц┌╞Ц┌╧Ц┐■Ц┐ЁЦ│▄Ц│▀Ц│▀Ц┌▀Ц┐°Ц┐╪Ц┐╚Ц│╚Д╫°Г■╗Ц│≥Ц┌▀Ц┐·Ц┌╟Ц┐▄Ц┌╧Е┼⌡Ц─┌Е╟▐Ц│∙Ц│▐Е├├Ц┌▓Ф▐▐Ц│▐Ц┌┬Ц│├Ц│╙Ф⌡╡Г╥ Ц│╞Ц─│Е╬▄Ф√╧Д╧╠Ф╟≈Ф╣│ Ц┌▓Х║╗Ц│≈Ц│╕Ц│└Ц┌▀Ц─┌Ф╟≈Ф╣│Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│╝Е⌡·Х╩╒Ф√╧Е░▒Ц│╚Е│▐Е░▒Ц│≈Ц│╕Ц│└Ц┌▀Ц─┌ Е█⌠Г░┐ Ц│╚Ц│┼Ц│└Ц│╕Ц│╞Ц─│Ц┐■Ц┐ЁЦ┐²Ц┐ЁГ▌┴Ц│╝Х╩▄И│⌠О╪┬
#Ц┐·Ц┌╟Ц┐▄Ц┌╧Е┼╧Ф·° О╪┴Ц┌└Е█⌠Г░┐Е▐╟Ц│╚Х║²Г╙│Ц│≈Ц│÷Е╬▄Ц│╝Ф▄≥Е▀∙О╪┬
#Ц┌╧Ц┐■Ц┐ЁЦ│╗Х║²Г╙│Ф≥┌Ц│╝Х╖▓Е╨╕ О╪┴Ц┌▓Е┬╤Е╬║Ц│≥Ц┌▀Ц│÷Ц┌│Ц│╚Ц─│И│╦Ф┴▀Ц│▄Ц┐■Ц┐ЁЦ┐²Ц┐ЁГ▌┴Ц│╚Е⌡·Х╩╒Ц┌▓Д╦▌Ц│┬Ц┌▀Ц│⌠Ц│╗Ц│▄Ц│┌Ц┌▀Ц─┌
Ц┐┬Ц┐┐Ц┐≈Ц┌╧Ц┐■Ц┐Ё Ц┌▓Ц│▀Ц│▒Ц┌▀Ц│╗Ц─│Ц┌┬Ц┌┼И│═Ц│▐Ц│╖Ф°─И╚≤Г┌╧Ц│╚И│■Ц│≈Ц─│Ц│²Ц│╝Е╬▄Ф─╔И─÷Ц│╚Х░╫Д╦▀Ц│≥Ц┌▀Ц─┌Е█⌠Г░┐Е▐╟Ц│╚Х║²Г╙│Е╬▄Ц│╞Ц│∙Ц┌┴Ц│╚Е┴█Ф√╧Ц│╦И─╡Ц│©Ц─│Г⌡╦Ф┴▀Ц│╝
Ц┐╘Ц┌╠Ц┐┐Ц┐┬ Ц│╚Е╫⌠Ц│÷Ц│ёЦ│÷Ц┐°Ц┐╪Ц┐╚Ц│╞Д╦┼Ф√╧Ц│╦Х╥ЁЦ│╜Д╦┼Ц│▄Ц┌▀Е┌╬Е░▒Ц│╚Ц│┌Ц┌▀Ц─┌
Ц┐░Ц┐┐Ц┌╞Ц┌╧Ц┐■Ц┐Ё Ц┌▓Ц│▀Ц│▒Ц│÷Е═╢Е░┬Ц│╞Ц─│Ц│⌠Ц│╝И─├Ц│╝Е┌╬Е░▒Ц┌▓Ц│╗Ц┌▀Ц─┌
Ц┐°Ц┐╪Ц┐╚Ц│╝Ц┌╧Ц┐■Ц┐Ё Ц│╞Ц─│Ц┐·Ц┌╟Ц┐▄Ц┌╧Е┼╧Ф·° Ц┌▓И─ Ц│≤Ц│╕Ц│²Ц│╝Е╪╬И│⌠Ц│╚Е╫╠И÷©Ц┌▓Д╦▌Ц│┬Ц┌▀Ц─┌Ц┌╞Ц┐┐Ц┌©Ц┐╩Ц┌╦Ц┐╔Ц┌ЁЦ┐╪Ц┐∙Ц┌╧Ц┌╜Ц┐╪Ц│╝Е╝ Г░├ Ц│╚Ц┌┬Ц┌▄Ц│╟Ц─│Г╘╨Ф╟≈Ц┌▓И²·Г╡≤Ф─╖Ф╣│Д╫⌠ Ц│╗Д╩╝Е╝ Ц│≈Ц│²Ц│╝Д╦╜Ц┌▓Е⌡·Х╩╒Ц│≥Ц┌▀Г░┐Ц┌▓Х─┐Ц│┬Ц┌▀Ц│╗Ц─│Ц┐·Ц┌╟Ц┐▄Ц┌╧Е┼⌡Ц│╞Д╩╔Д╦▀Ц│╝Ц┌┬Ц│├Ц│╚Х║╗Ц│⌡Ц┌▀[ 21]
F
M
=
8
3
о─
r
3
о│
о┴
v
{\displaystyle F_{\text{M}}={\frac {8}{3}}\pi r^{3}\rho \omega v}
Ц│⌠Ц│⌠Ц│╖Ц─│r Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│╝Е█┼Е╬└Ц─│о┴ Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│╝Х╖▓И─÷Е╨╕ Ц─│о│ Ц│╞Г╘╨Ф╟≈Е╞├Е╨╕Ц─│v Ц│╞Г╘╨Ф╟≈Ц│╚Е╞╬Ц│≥Ц┌▀Ц┐°Ц┐╪Ц┐╚Ц│╝И─÷Е╨╕Ц│╖Ц│┌Ц┌▀Ц─┌Ц┐·Ц┌╟Ц┐▄Ц┌╧Е┼⌡Ц│╞Ц─│И│▀Е▀∙Ф√╧Е░▒Ц│╗Е⌡·Х╩╒Х╩╦Ц│╝Ц│²Ц┌▄Ц│·Ц┌▄Ц│╚Е╞╬Ц│≈Ц│╕Е·┌Г⌡╢Ц│╙Е░▒Ц│█Ц│╚Е┐█Ц│▐[ 22]
о┴
^
ц≈
v
{\displaystyle \textstyle {\hat {\mathbf {\omega } }}\times \mathbf {v} }
[ 22] [ 23] Г╡≤Ф─╖ Ц┌▓Ф▄│Ц│ёЦ│╕Ц│┼Ц┌┼Ц─│Ц│²Ц│╝Е═╢Е░┬Ц│╝Ц┐·Ц┌╟Ц┐┼Ц┌╧Е┼⌡Ц│╞Д╩╔Д╦▀Ц│╝Ц┌┬Ц│├Ц│╚Х║╗Ц│∙Ц┌▄Ц┌▀[ 24]
F
M
=
1
2
о│
C
L
A
v
2
{\displaystyle F_{\text{M}}={\frac {1}{2}}\rho C_{\text{L}}Av^{2}}
Ц│⌠Ц│⌠Ц│╖Ц─│о│ Ц│╞Г╘╨Ф╟≈Е╞├Е╨╕Ц─│C L Ц│╞Ф▐ Е┼⌡Д©┌Ф∙╟ Ц─│A Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│╝Ф√╜И²╒Г╘█Ц─│v Ц│╞Г╘╨Ф╟≈Ц│╚Е╞╬Ц│≥Ц┌▀Ц┐°Ц┐╪Ц┐╚Ц│╝И─÷Е╨╕Ц│╖Ц│┌Ц┌▀Ц─┌Ф▐ Е┼⌡Д©┌Ф∙╟Ц│╞Х╓┤И⌡▒Ц│╙Ц┐▒Ц┐╘Ц┐║Ц┐╪Ц┌©Ц│╖Ц─│rо┴ /v Ц│╖Х║╗Ц│∙Ц┌▄Ц┌▀Ф╞■Ц┌└Ц┐╛Ц┌╓Ц┐▌Ц┐╚Ц┌╨Ф∙╟Ц─│И²╒Ц│╝Г╡≈Ц│∙ Г╜┴Ц│╚Д╬²Е╜≤Ц│≥Ц┌▀[ 24] И─├Ц┐·Ц┌╟Ц┐▄Ц┌╧Е┼╧Ф·° О╪┴[ 6] [ 25] [ 26]
Ц┐├Ц┐▀Ц┌╧ Ц┌└Ц┐░Ц┐╛Ц┐╪Ц┐°Ц┐╪Ц┐╚ Ц│╙Ц│╘Ц│╝Ц┌╧Ц┐²Ц┐╪Ц┐└Ц│╖Ц│╞Ц─│Ц┐≈Ц┐╛Ц┐╪Ц┐╓Ц┐╪Ц│╞Ц┐·Ц┌╟Ц┐▄Ц┌╧Е┼╧Ф·°Ц┌▓Е┬╘Г■╗Ц│≈Ц│╕Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╝Е╪╬И│⌠Ц┌▓Е┬╤Е╬║Ц│≥Ц┌▀Ц│⌠Ц│╗Ц│▄Ц│╖Ц│█Ц┌▀О╪┬Ц┐┬Ц┐┐Ц┐≈Ц┌╧Ц┐■Ц┐Ё Ц┌└Ц┐░Ц┐┐Ц┌╞Ц┌╧Ц┐■Ц┐Ё О╪┬Х▀╠Х╙·Г┴┬ О╪┴ Ц┌╢Ц┐╚Ц┐∙ Ц│╚Ц│┼Ц│└Ц│╕Ц│╞Ц─│И─ Е╦╦Ц┌╢Ц┐╚Ц┐∙Ц┌║Ц┐╪Ц│╚Д╦█Е┬╘Г⌡┼Ц│╗Ц│╙Ц┌▀Ц┌╧Ц┐╘Ц┌╓Ц┌╧Ц┌└Ц┐∙Ц┐┐Ц┌╞ Ц│╝Е▌÷Е⌡═Ц│╗Ц│╙Ц┌▀Ц│▄Ц─│Ц┐├Ц┌ёЦ┐╪Ц┌╥Ц┐╖Ц┐┐Ц┐┬ Ц┌└Ц│²Ц│╝Д╩√Ц│╝Ц┌╥Ц┐╖Ц┐┐Ц┐┬Ц│╝Иё⌡Х╥²И⌡╒Ц┌▓Ц│┌Ц│▓Ц┌▀Ц│╝Ц│╚Е╫╧Г╚▀Ц│╓Ц│⌠Ц│╗Ц┌┌Ц│┌Ц┌▀[ 27] [ 28] И┤▌Г░┐ Ц│╖Ц│╞Ц─│Ф┼∙Ф┴▀ Ц│▄Ц┐·Ц┌╟Ц┐┼Ц┌╧Е┼╧Ф·°Ц┌▓Е┬╘Г■╗Ц│≥Ц┌▀Ц│⌠Ц│╗Ц│╖Ц┌╚Ц┐╪Ц┐√ Ц│╙Ц│╘Ц│╝Е╓┴Е▄√Г░┐ Ц┌▓Ф┼∙Ц│▓Ц┌▀Ц│⌠Ц│╗Ц│▄Ц│╖Ц│█Ц┌▀[ 29]
Ц┐°Ц┐╪Ц┐╚Ц│╝Ф■╧И─═ Ц│▄Е▐█Е┴┤Ц│╚Ц│╙Ц┌▀Ц│⌠Ц│╗Ц┌┌Ц│┌Ц┌▀Ц─┌Ц┌╞Ц┐╙Ц┌╠Ц┐┐Ц┐┬ Ц│╖Ц│╞Ц─│2006Е╧╢8Ф°┬Ц│╝Ц┌╓Ц┐ЁЦ┌╟Ц┐╘Ц┐ЁЦ┐┴Ц│╗Ц┐▒Ц┌╜Ц┌╧Ц┌©Ц┐ЁЦ│╝Х╘╕Е░┬ (en:2006 ball-tampering controversy ) Ц│╚И√╒И─ёЦ│≈Ц│╕Х╜╟Х╚√Ц│╝Г └Ц│╚Ц│╙Ц│ёЦ│÷[ 30] Г╘╨Ф╟≈Е┼⌡Е╜╕ Г └Ф─╖ХЁ╙Ц┌▓Е╓┴Ц│┬Ц┌▀Ц│÷Ц┌│Ц│╚Ц─│Е■╬Ф╤╡Ц┌└Ф²╬Х└┌ Ц│╗Ц│└Ц│ёЦ│÷Ц┌┌Ц│╝Ц│╖Ц┐°Ц┐╪Ц┐╚Ц┌▓Ц┌ЁЦ┐╪Ц┐├Ц┌ёЦ┐ЁЦ┌╟Ц│≥Ц┌▀Ц│⌠Ц│╗Ц┌▓Ф▄┤Ц│≈Ц─│Ц┐║Ц┌╦Ц┐ёЦ┐╪Ц┐╙Ц┐╪Ц┌╟Ц┌└Ф≈╔Ф°╛Ц│╝Ц┐≈Ц┐╜И┤▌Г░┐Ц│╖Ц│╞Х╕▐Е┴┤Ц│╖Г╕│Ф╜╒Ц│∙Ц┌▄Ц│╕Ц│└Ц┌▀Х║▄Г┌╨Ц│╖Ц│┌Ц┌▀[ 31] [ 32]
Ф╟╢Ц┌└Г╘╨Ф╟≈Ц│╙Ц│╘Ц│╝Ф╣│Д╫⌠ Д╦╜Ц│╚Ц│┌Ц┌▀Г┴╘Д╫⌠Ц│╞Ц─│Ф╣╝Е┼⌡ Ц│╗Е▒╪Ц│╟Ц┌▄Ц┌▀Д╦┼Е░▒Ц│█Ц│╝Е┼⌡Ц┌▓Е▐≈Ц│▒Ц┌▀Ц─┌Ц┌╒Ц┐╚Ц┌╜Ц┐║Ц┐┤Ц┌╧Ц│╝Е▌÷Г░├ Ц│╚Ц┌┬Ц┌▄Ц│╟Ц─│Ф╣╝Е┼⌡Ц│╝Е╓╖Ц│█Ц│∙Ц│╞Г┴╘Д╫⌠Ц│╚Ц┌┬Ц│ёЦ│╕Ф┼╪Ц│≈Ц│╝Ц│▒Ц┌┴Ц┌▄Ц│÷Ф╣│Д╫⌠Ц│╝И┤█И┤▐Ц│╗Г╜┴Ц│≈Ц│└Ц─┌Г░┐Ц┌▓Х─┐Ц│┬Ц┌▀Ц│╗Ц─│Ф╣╝Е┼⌡О╪┬F B О╪┴Ц│╝Е╓╖Ц│█Ц│∙Ц│╞Ф╛║Ц│╝Ц┌┬Ц│├Ц│╚Х║╗Ц│⌡Ц┌▀[ 35]
F
B
=
4
3
о─
r
3
о│
g
{\displaystyle F_{\text{B}}={\frac {4}{3}}\pi r^{3}\rho g}
Ц│⌠Ц│⌠Ц│╖Ц─│r Ц│╞Г░┐Ц│╝Е█┼Е╬└Ц─│о│ Ц│╞Ф╣│Д╫⌠Ц│╝Е╞├Е╨╕Ц─│g Ц│╞И┤█Е┼⌡Е┼═И─÷Е╨╕Ц│╖Ц│┌Ц┌▀Ц─┌Ф╣╝Е┼⌡Ц│╞Г╘╨Ф╟≈Д╦╜Ц│╚Ц│┼Ц│└Ц│╕Ц│╞Ц─│Ц│÷Ц│└Ц│╕Ц│└Ц│╝Е═╢Е░┬Ц─│Ф┼≈Е┼⌡Ц┌└Ц┐·Ц┌╟Ц┐┼Ц┌╧Е┼⌡Ц│╚Ф╞■Ц│╧Ц│╕Е╟▐Ц│∙Ц│▐Г└║Х╕√Ц│╖Ц│█Ц┌▀Ц─┌Ц│÷Ц│═Ц│≈Д╬▀Ц│┬Ц│╟Ц┐░Ц┌╧Ц┌╠Ц┐┐Ц┐┬Ц┐°Ц┐╪Ц┐╚ Ц│╝Е═╢Е░┬Ц│╚Ц│╞Ц─│Ц│²Ц│╝Е╝╧Г╘█Ц│╚Ф╞■Ц│╧Ц┌▀Ц│╗Х╩╫Ц│└Ц│÷Ц┌│Ф╣╝Е┼⌡Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│╝И┤█И┤▐Ц│╝Г╢└1.5О╪┘Ц│╚И│■Ц│≥Ц┌▀Ц│⌠Ц│╗Ц┌┌Ц│┌Ц┌┼Ц─│Г└║Х╕√Ц│╖Ц│█Ц│╙Ц│▐Ц│╙Ц┌▀Ц─┌
Д╩√Ц│╝Г┴╘Д╫⌠Х║╗И²╒Ц│╚Х║²Г╙│Ц│≥Ц┌▀Ц┐°Ц┐╪Ц┐╚Ц│╝Е°╖Г╦╝О╪┬AБ├▓BО╪┴Ц│╗Х├╗Е╪╣О╪┬BБ├▓CО╪┴Ц─┌Х║²Г╙│Ф≥┌Ц│╚Е▐≈Ц│▒Ц┌▀Е┼⌡Ц│╞И─ Е╦╦Ц─│(Г┴╧Ц│╚Е°╖Г╦╝Ц│▄Е╟▐Ц│∙Ц│└Е═╢Е░┬Ц│╚Ц│╞)Е°╖Г╦╝Ц│∙Ц┌▄Ц│÷Е╧┘Ц│╚Ф╞■Д╬▀Ц│≈Ц─│Ц│╟Ц│╜Е┼⌡ Ц│╗Ц│≈Ц│╕Ц┐╒Ц┐┤Ц┐╚Е▄√Ц│╖Ц│█Ц┌▀[ 38] [ 39] Ц┐°Ц┐╪Ц┐╚Ц│▄Д╩√Ц│╝Г┴╘Д╫⌠Х║╗И²╒Ц│╚Х║²Г╙│ Ц│≥Ц┌▀Ц│╗Ц─│Ц┐°Ц┐╪Ц┐╚Ц│═Ц│▒Ц│╖Ц│╙Ц│▐Г┴╘Д╫⌠Х║╗И²╒Ц┌┌Е▐█Г≥╨ Ц─│Ф▄╞Е▀∙Ц│≈Ц─│И÷Ё Ц┌└Г├╠ Ц│╙Ц│╘Ц│▄Г≥╨Г■÷Ц│≥Ц┌▀Ц│÷Ц┌│Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╞И│▀Е▀∙Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪ Ц┌▓Е╓╠Ц│├Ц─┌Ц│∙Ц┌┴Ц│╚Ц─│Х║²Г╙│Ф≥┌Ц│╝Х║²Ф▓┐Ц│╚Ц┌┬Ц┌┼Ц┐°Ц┐╪Ц┐╚Ц│╞Д╦─Е╝ Ц│╝Е⌡·Х╩╒Ф┬░Е┬├Ц┌▓Е╬≈Ц┌▀Ц│÷Ц┌│Ц─│Ц┐°Ц┐╪Ц┐╚Ц│▄Ф▄│Ц│ёЦ│╕Ц│└Ц┌▀Д╦╕И─╡И│▀Е▀∙Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪ Ц│╝Д╦─И┐╗Ц│▄Е⌡·Х╩╒И│▀Е▀∙Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪Ц│╚Е╓┴Ф▐⌡Ц│∙Ц┌▄Ц┌▀Ц│⌠Ц│╗Ц┌┌Ц│┌Ц┌▀[ 41] Е▐█Г≥╨Д©┌Ф∙╟ О╪┬CORЦ─│Е╪▐Ц│╚Ц│┼Ц│└Ц│╕Ц│╞e Ц│╖Х║╗Ц│∙Ц┌▄Ц┌▀О╪┴Ц│╚Ц┌┬Ц│ёЦ│╕О╪┬И√⌠Ф▌╔Г └Ц│╚О╪┴Г┴╧Е╬╢Д╩≤Ц│▒Ц┌┴Ц┌▄Ц┌▀[ 42]
e
=
Б┬▓
v
f
Б┬▓
u
f
v
i
Б┬▓
u
i
{\displaystyle e=-{\frac {v_{\text{f}}-u_{\text{f}}}{v_{\text{i}}-u_{\text{i}}}}}
Ц│⌠Ц│⌠Ц│╖Ц─│v f Ц─│v i Ц│╞Ц│²Ц┌▄Ц│·Ц┌▄Ц┐°Ц┐╪Ц┐╚Ц│╝Х║²Г╙│Г⌡╢Е╬▄Ц─│Х║²Г╙│Г⌡╢Е┴█Ц│╝И─÷Е╨╕Ц│╖Ц│┌Ц┌┼Ц─│u f Ц─│u i Ц│╞Ц│²Ц┌▄Ц│·Ц┌▄Ц─│Ц┐°Ц┐╪Ц┐╚Ц│▄Х║²Г╙│Ц│≥Ц┌▀Е╞╬Х╠║Ц│╖Ц│┌Ц┌▀Г┴╘Д╫⌠Х║╗И²╒Ц│╝Х║²Г╙│Г⌡╢Е╬▄Ц─│Х║²Г╙│Г⌡╢Е┴█Ц│╝И─÷Е╨╕Ц┌▓Х║╗Ц│≥[ ФЁ╗И┤┬ 3] [ 43]
e
=
Б┬▓
v
f
v
i
{\displaystyle e=-{\frac {v_{\text{f}}}{v_{\text{i}}}}}
Ц│≈Ц│÷Ц│▄Ц│ёЦ│╕Ц─│Ц┐°Ц┐╪Ц┐╚Ц│▄Е╨┼Ц│╚Х░╫Д╦▀Ц│≈Ц│╕Х║²Г╙│Ц│≥Ц┌▀Е═╢Е░┬Ц┌▓Х─┐Ц│┬Ц┌▀Ц│╗Ц─│Е▐█Г≥╨Д©┌Ф∙╟Ц│╞0О╪┬Е┘╗Ц│▐Х╥ЁЦ│╜Х©■Ц┌┴Ц│╙Ц│└Е═╢Е░┬Ц─┌Ц┐°Ц┐╪Ц┐╚Ц│▄Ф▄│Ц│╓И│▀Е▀∙Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪Ц│╞Х║²Г╙│Ц│╚Ц┌┬Ц│ёЦ│╕Ц│≥Ц│╧Ц│╕Е╓╠Ц┌▐Ц┌▄Ц┌▀О╪┴Ц│╗1О╪┬Х║²Г╙│Е┴█Ц│╗Е░▄Ц│≤И─÷Ц│∙Ц│╖Х╥ЁЦ│╜Х©■Ц┌▀Е═╢Е░┬Ц─┌Х║²Г╙│Ц│╚Ц┌┬Ц┌┼Д╦─Е┬┤И│▀Е▀∙Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪Ц┌▓Е╓╠Ц┌▐Ц│╙Ц│└О╪┴Ц│╝И√⌠Ц│╖Е╓┴Е▄√Ц│≥Ц┌▀Ц─┌0Ф°╙Ф╨─Ц│┌Ц┌▀Ц│└Ц│╞1Ц┌▓Х╤┘Ц│┬Ц┌▀Ц┌┬Ц│├Ц│╙Е▐█Г≥╨Д©┌Ф∙╟Ц┌┌Ц─│Г░├Х╚√Д╦┼Ц│╞Х─┐Ц│┬Ц┌▀Ц│⌠Ц│╗Ц│▄Ц│╖Ц│█Ц┌▀Ц─┌e < 0e > 1[ 45] [ 46]
И│▀Е▀∙Ц│╝Е·┌Г⌡╢Ф√╧Е░▒Ф┬░Е┬├Ц│╗Ф╟╢Е╧ЁФ√╧Е░▒Ф┬░Е┬├Ц┌▓Е┬├Ц│▒Ц│╕Х╖ёФ·░Ц│≥Ц┌▀Г⌡╝Г └Ц│╖Ц─│Е▐█Г≥╨Д©┌Ф∙╟Ц│╝Г┴╘Д╫⌠Х║╗И²╒Ц│╚Е╞╬Ц│≥Ц┌▀ФЁ∙Г╥ Ф√╧Е░▒Ф┬░Е┬├О╪┬e y О╪┴Ц│╗Ф▌╔Г╥ Ф√╧Е░▒Ф┬░Е┬├ О╪┬e x О╪┴Ц│╚Е┬├Х╖ёЦ│∙Ц┌▄Ц┌▀Ц│⌠Ц│╗Ц┌┌Ц│┌Ц┌▀Ц─┌Ц│⌠Ц┌▄Ц│╞Д╩╔Д╦▀Ц│╝Ц┌┬Ц│├Ц│╚Е╝ Г╬╘Ц│∙Ц┌▄Ц┌▀Ц─┌
e
y
=
Б┬▓
v
y
f
Б┬▓
u
y
f
v
y
i
Б┬▓
u
y
i
{\displaystyle e_{y}=-{\frac {v_{y{\text{f}}}-u_{y{\text{f}}}}{v_{y{\text{i}}}-u_{y{\text{i}}}}}}
e
x
=
Б┬▓
(
v
x
f
Б┬▓
r
о┴
f
)
Б┬▓
(
u
x
f
Б┬▓
R
н╘
f
)
(
v
x
i
Б┬▓
r
о┴
i
)
Б┬▓
(
u
x
i
Б┬▓
R
н╘
i
)
{\displaystyle e_{x}=-{\frac {(v_{x{\text{f}}}-r\omega _{\text{f}})-(u_{x{\text{f}}}-R\Omega _{\text{f}})}{(v_{x{\text{i}}}-r\omega _{\text{i}})-(u_{x{\text{i}}}-R\Omega _{\text{i}})}}}
Ц│⌠Ц│⌠Ц│╖Ц─│r Ц│╗о┴ Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│╝Е█┼Е╬└Ц│╗Х╖▓И─÷Е╨╕Ц│╖Ц│┌Ц┌┼Ц─│R Ц│╗н╘ Ц│╞Х║²Г╙│И²╒О╪┬И┤▌Г░┐Ц│╝Ц┐░Ц┐┐Ц┐┬Ц│╙Ц│╘Ц│▄Д╦─Д╬▀О╪┴Ц│╝Е█┼Е╬└Ц│╗Х╖▓И─÷Е╨╕Ц┌▓Х║╗Ц│≥Ц─┌Г┴╧Ц│╚Ц─│rо┴ Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│╝Х║╗И²╒Ц│╚Ц│┼Ц│▒Ц┌▀Ф▌╔Г╥ Ф√╧Е░▒Ц│╝И─÷Ц│∙Ц│╖Ц─│Rн╘ Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│▄Х║²Г╙│Ц│≈Ц│÷Г┴╘Д╫⌠Ц│╝Х║²Ф▓┐И²╒Ц│╚Ц│┼Ц│▒Ц┌▀Ф▌╔Г╥ Ф√╧Е░▒Ц│╝И─÷Ц│∙Ц│╖Ц│┌Ц┌▀Ц─┌Ц│⌠Ц│├Ц│≈Ц│÷Х╖ёФ·░Ц│╞Ц─│Ц┐°Ц┐╪Ц┐╚Ц│▄Ф√°Ц┌│Ц│╝Х╖▓Е╨╕ Ц│╖Х║╗И²╒Ц│╚Х║²Г╙│Ц│≥Ц┌▀Е═╢Е░┬Ц─│Ц│┌Ц┌▀Ц│└Ц│╞Е⌡·Х╩╒ Ц┌▓Х─┐Ф┘╝Ц│≥Ц┌▀Е©┘Х╕│Ц│▄Ц│┌Ц┌▀Е═╢Е░┬Ц│╚Г■╗Ц│└Ц┌┴Ц┌▄Ц┌▀Ц─┌
Ц┐°Ц┐╪Ц┐╚Ц│╚Д╫°Г■╗Ц│≥Ц┌▀Е┼⌡Ц┌▓И┤█Е┼⌡Ц│╝Ц│©Ц│╗Д╩╝Е╝ Ц│≈Ц─│Ц│∙Ц┌┴Ц│╚Ц┐°Ц┐╪Ц┐╚Ц│▄Е⌡·Х╩╒Ц│⌡Ц│ Ц│╚Е°╟И²╒Ц│╚Ц│╬Ц│ёЦ│≥Ц│░Х░╫Д╦▀Ц│≥Ц┌▀Е═╢Е░┬Ц│╚Ц│╞Ц─│Е▐█Г≥╨Д©┌Ф∙╟Ц│╞Ф╛║Ц│╝Ц┌┬Ц│├Ц│╚Д╩√Ц│╝Ц│└Ц│▐Ц│╓Ц│▀Ц│╝Г┴╘Г░├И┤▐Ц│╗И√╒И─ёД╩≤Ц│▒Ц┌▀Ц│⌠Ц│╗Ц│▄Ц│╖Ц│█Ц┌▀[ 39] [ 49]
e
=
|
v
f
v
i
|
=
K
f
K
i
=
U
f
U
i
=
H
f
H
i
=
T
f
T
i
=
g
T
f
2
8
H
i
{\displaystyle e=\left|{\frac {v_{\text{f}}}{v_{\text{i}}}}\right|={\sqrt {\frac {K_{\text{f}}}{K_{\text{i}}}}}={\sqrt {\frac {U_{\text{f}}}{U_{\text{i}}}}}={\sqrt {\frac {H_{\text{f}}}{H_{\text{i}}}}}={\frac {T_{\text{f}}}{T_{\text{i}}}}={\sqrt {\frac {gT_{\text{f}}^{2}}{8H_{\text{i}}}}}}
Ц│⌠Ц│⌠Ц│╖Ц─│K Ц│╗U Ц│╞Ц│²Ц┌▄Ц│·Ц┌▄Ц┐°Ц┐╪Ц┐╚Ц│▄Ф▄│Ц│╓И│▀Е▀∙Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪ Ц│╗Д╫█Г╫╝Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪ Ц│╖Ц│┌Ц┌┼Ц─│H Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│▄Е┬╟И│■Ц│≥Ц┌▀Ф°─Е╓╖Ц│╝И╚≤Ц│∙Ц─│T Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│╝Иё⌡Г©■Ц│≥Ц┌▀Ф≥┌И√⌠Ц┌▓Х║╗Ц│≥Ц─┌ iЦ│┼Ц┌┬Ц│ЁfЦ│╝Ф╥╩Е╜≈Ц│╞Ц│²Ц┌▄Ц│·Ц┌▄Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╝Х║²Г╙│Е┴█Ц─│Х║²Г╙│Е╬▄Ц│╝Г┼╤Ф┘▀Ц┌▓Х║╗Ц│≥Ц─┌Е░▄Ф╖≤Ц│╚Ц─│Х║²Ф▓┐Ф≥┌Ц│╚Е╓╠Ц┌▐Ц┌▄Ц┌▀Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪Ц┌┌Ц─│Ф╛║Ц│╝Ц┌┬Ц│├Ц│╚Е▐█Г≥╨Д©┌Ф∙╟Ц┌▓Г■╗Ц│└Ц│╕Х║╗Ц│≥Ц│⌠Ц│╗Ц│▄Ц│╖Ц│█Ц┌▀Ц─┌
Energy Loss
=
K
i
Б┬▓
K
f
K
i
ц≈
100
%
=
(
1
Б┬▓
e
2
)
ц≈
100
%
{\displaystyle {\text{Energy Loss}}={\frac {{K_{\text{i}}}-{K_{\text{f}}}}{K_{\text{i}}}}\times 100\%=\left(1-e^{2}\right)\times 100\%}
Ц┐°Ц┐╪Ц┐╚Ц│╝Е▐█Г≥╨Д©┌Ф∙╟Ц│╞Ц─│Х╓┤Ф∙╟Ц│╝Ф²║Д╩╤Ц│╚Ц┌┬Ц│ёЦ│╕Е╓┴Е▄√Ц│≥Ц┌▀Ц─┌Д╦▀Х╗≤Ц│╞Ц│²Ц│╝Ф²║Д╩╤Ц│╝Д╬▀Ц│╖Ц│┌Ц┌▀Ц─┌
Х║²Г╙│Ц│≥Ц┌▀И²╒Ц│╝Ф─╖ХЁ╙О╪┬Д╬▀О╪ Х█┴Ц─│Ц┌ЁЦ┐ЁЦ┌╞Ц┐╙Ц┐╪Ц┐┬Ц─│И┤▒Г╤╡О╪┴[ 49] [ 51]
Ц┐°Ц┐╪Ц┐╚Ц│╝Г╢═Ф²░О╪┬И²╘Ц─│Ц┌╢Ц┐═Ц─│Ц┐≈Ц┐╘Ц┌╧Ц┐│Ц┐┐Ц┌╞Ц│╙Ц│╘О╪┴[ 39]
Ц┐°Ц┐╪Ц┐╚Е├┘Ц│╝Е°╖Е┼⌡О╪┬Д╦╜Г╘╨Ц│╝Е═╢Е░┬О╪┴[ 39]
Х║²Г╙│Ф≥┌Ц│╚Ц┐°Ц┐╪Ц┐╚Ц│╚Г■÷Ц│≤Ц┌▀Е⌡·Х╩╒И┤▐[ 52]
Х║²Г╙│Ф≥┌Ц│╝И─÷Е╨╕[ 38] [ 39] [ 51] [ 53] Д╦┼Х╗≤Д╩╔Е╓√Ц│╚Ц┌┌Ц─│Д╬▀Ц│┬Ц│╟Ф╦╘Е╨╕ Ц│╙Ц│╘Ц│╝Е╓√И┐╗Ф²║Д╩╤Ц│╚Ц┌┬Ц┌┼Ц─│Х║²Г╙│И²╒Ц│╬Ц│÷Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│╝Г┴╧Ф─╖Ц│▄Е╓┴Е▄√Ц│≈Ц─│Е┴⌡Ф─╖ Ц┌└Е╪╬Ф─╖Ц│▄Е╓┴Е▄√Ц│≥Ц┌▀Ц│⌠Ц│╗Ц┌┌Ц│┌Ц┌▀Ц─┌Ц│⌠Ц│├Ц│≈Ц│÷Е╓┴Е▄√Ц┌┌Ц─│Е▐█Г≥╨Д©┌Ф∙╟Ц│╚Е╫╠И÷©Ц┌▓Д╦▌Ц│┬Ц┌▀[ 39] [ 39] [ 53]
Е⌡·Х╩╒Ц│≈Ц│╙Ц│▄Ц┌┴Е╨┼И²╒Ц│╚Х║²Г╙│Ц│≥Ц┌▀Ц┐°Ц┐╪Ц┐╚Ц│╚Ц│▀Ц│▀Ц┌▀Е┼⌡Ц─┌Д╦╩Ц│╚Ц─│И┤█Е┼⌡Ц─│Е·┌Г⌡╢Ф┼≈Е┼⌡ Ц─│Ф▒╘Ф⌠╕Е┼⌡Ц│▄Ф▄≥Ц│▓Ц┌┴Ц┌▄Ц┌▀О╪┬Ф▒╘Ф⌠╕Е┼⌡Ц│╞Д╦╕И─╡Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪Ц│╚Ц┌┌Е⌡·Х╩╒Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪Ц│╚Ц┌┌Е╫╠И÷©Ц│≥Ц┌▀О╪┴Ц─┌Ц┌┌Ц│≈Е╨┼И²╒Ц│▄Е┌╬Ц│└Ц│╕Ц│└Ц┌▀Е═╢Е░┬Ц─│И┤█Е┼⌡Ц│╝Е░▒Ц│█Ц│╞Е╨┼И²╒Ц│╚Е╞╬Ц│≈Ц│╕Е░▄Ц│≤Х╖▓Е╨╕Ц│═Ц│▒Е┌╬Ц│▐Ц│▄Ц─│Д╩√Ц│╝Е┼⌡Ц│╞Е╨┼Ц│▄Е┌╬Ц│└Ц│╕Ц│└Ц┌▀Ц│╗Ц│≈Ц│╕Ц┌┌Ц│²Ц│╝Е┌╬Ц│└Ц│÷Е╨┼Ц│╚Е╞╬Ц│≈Ц│╕Ф╟╢Е╧ЁЦ─│Ц┌┌Ц│≈Ц│▐Ц│╞Е·┌Г⌡╢Ц│╙Ф√╧Е░▒Ц│╚Е┐█Ц│▐Ц─┌ Е°╟И²╒Ц│╚Х║²Г╙│Ц│≥Ц┌▀Ц│╗Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╝Х║²Г╙│Х╖▓Е╨╕Ц┌└Х╖▓И─÷Е╨╕Ц│╚Е©°Ц│≤Ц│╕Ц─│Д╦╕И─╡И│▀Е▀∙Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪ Ц│╝Д╦─И┐╗Ц│▄Е⌡·Х╩╒И│▀Е▀∙Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪Ц│╚Е╓┴Ф▐⌡Ц│∙Ц┌▄Ц│÷Ц┌┼Ц─│Ц│┌Ц┌▀Ц│└Ц│╞И─├Ц│╚Е⌡·Х╩╒И│▀Е▀∙Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪Ц│╝Д╦─И┐╗Ц│▄Д╦╕И─╡И│▀Е▀∙Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪Ц│╚Е╓┴Ф▐⌡Ц│∙Ц┌▄Ц┌▀Ц│⌠Ц│╗Ц│▄Ц│┌Ц┌▀Ц─┌Ц┐°Ц┐╪Ц┐╚Ц│▄Х║²Г╙│Ф≥┌Ц│╚Е°╟И²╒Ц│╗Ф╟╢Е╧ЁЦ│╝Ф√╧Е░▒Ц│╚Е▀∙Ц│▐Е═╢Е░┬Ц─│Ф▒╘Ф⌠╕ Е┼⌡Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│╝И─╡Х║▄Ф√╧Е░▒Ц│╗Е▐█Е╞╬Ц│╝Е░▒Ц│█Ц│╝Ц─▄Д╦╕И─╡Ц─█Ф┬░Е┬├Ц┌▓Ф▄│Ц│╓Ц─┌Д╦┼Ц│╝Е⌡ЁЦ│╖Ц│╞Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╞Е▐ЁЦ│╚Г╖╩Е▀∙Ц│≈Ц│╕Ц│└Ц┌▀Ц│÷Ц┌│Ц─│Ф▒╘Ф⌠╕Е┼⌡Ц│╞Ц┐°Ц┐╪Ц┐╚Ц┌▓Е╥╕Ц│╚Ф┼╪Ц│≥Е░▒Ц│█Ц│╝Д╦╕И─╡Ф┬░Е┬├Ц┌▓Е░╚Ц┌─Ц─┌Ц│∙Ц┌┴Ц│╚Ц─│Ц┐°Ц┐╪Ц┐╚Ц│▄Х║²Г╙│Ф≥┌Ц│╚Е⌡·Х╩╒Ц│≈Ц│╕Ц│└Ц┌▀Е═╢Е░┬Ц─│Ф▒╘Ф⌠╕Е┼⌡Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│╝Е⌡·Х╩╒Ц│╗Е▐█Е╞╬Ц│╝Е░▒Ц│█Ц│╝Ц─▄Е⌡·Х╩╒Ц─█Ф┬░Е┬├Ц┌▓Ф▄│Ц│╓Ц─┌Ц│⌠Ц│╝Е⌡ЁЦ│╖Ц│╞Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╞Ф≥┌Х╗┬Е⌡·Ц┌┼Ц│╚Е⌡·Х╩╒Ц│≈Ц│╕Ц│└Ц┌▀Ц│÷Ц┌│Ц─│Е°╟И²╒Ц│╗Х║²Г╙│Ц│≥Ц┌▀Г┌╧Ц│╞Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╝И┤█Е©┐ Ц│╚Е╞╬Ц│≈Ц│╕Е╥╕Ц│╚Г╖╩Е▀∙Ц│≈Ц│╕Ц│└Ц┌▀Ц─┌Ц│≈Ц│÷Ц│▄Ц│ёЦ│╕Ц─│Ф▒╘Ф⌠╕Ц│╝Е⌡·Х╩╒Ф┬░Е┬├Ц│╞Ц┐°Ц┐╪Ц┐╚Ц┌▓Е▐ЁЦ│╚Ф┼╪Ц│≥Е░▒Ц│█Ц│╚Е┐█Ц│▐Ц│⌠Ц│╗Ц│╚Ц│╙Ц┌▀Ц─┌Е·┌Г⌡╢Ф┼≈Е┼⌡Ц┌└И┤█Е┼⌡Ц│╗Ц│╞Г∙╟Ц│╙Ц┌┼Ц─│Ц│⌠Ц┌▄Ц┌┴Ц│╝Ф▒╘Ф⌠╕Е┼⌡Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│╚Ц┐┬Ц┐╚Ц┌╞ Ц┌▓Е▐┼Ц│╪Ц│≈Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╝Х╖▓И─÷Е╨╕О╪┬о┴ О╪┴Ц┌▓Е╓┴Е▄√Ц│∙Ц│⌡Ц┌▀Д╫°Г■╗Ц│▄Ц│┌Ц┌▀[ 54] [ 55] [ 56] [ 57]
Ц┐°Ц┐╪Ц┐╚Ц│╝Е⌡·Х╩╒Ц│╝Е╫╠И÷©Ц│╚Ц│╓Ц│└Ц│╕Ц│╞Д╩╔Д╦▀Ц│╝Ц┌┬Ц│├Ц│╙Д╨▀Д╬▀Ц│▄Х─┐Ц│┬Ц┌┴Ц┌▄Ц┌▀[ 57] [ 58] [ 59]
Ц┐°Ц┐╪Ц┐╚Ц│╚Ц┐░Ц┐┐Ц┌╞Ц┌╧Ц┐■Ц┐ЁЦ│▄Ц│▀Ц│▀Ц│ёЦ│╕Ц│└Ц┌▀Е═╢Е░┬Ц─│Д╦╕И─╡Ц│╚Ц┌┬Ц┌▀Ф▒╘Ф⌠╕Ц│╗Е⌡·Х╩╒Ц│╚Ц┌┬Ц┌▀Ф▒╘Ф⌠╕Ц│╞Е░▄Ц│≤Ф√╧Е░▒Ц│╚Д╫°Г■╗Ц│≥Ц┌▀Ц─┌Ц┐°Ц┐╪Ц┐╚Ц│╝Х╖▓И─÷Е╨╕Ц│╞Ц─│Ф╟╢Е╧ЁФ√╧Е░▒Ц│╝И─÷Е╨╕Ц│╗Е░▄Ф╖≤Ц│╚Х║²Г╙│Е╬▄Ц│╞Ф╦⌡Е╟▒Ц│≈Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╞Д╦┼Е░▒Ц│█Ц│╚Ф┼╪Ц│≈Е┤╨Ц│∙Ц┌▄Ц─│Е═╢Е░┬Ц│╚Ц┌┬Ц│ёЦ│╕Ц│╞Е┘┐Ц│╝И╚≤Ц│∙Ц┌▓Х╤┘Ц│┬Ц│╕Ц┐░Ц┌╕Ц┐ЁЦ┐┴Ц│≥Ц┌▀Ц│⌠Ц│╗Ц│∙Ц│┬Ц│┌Ц┌▀Ц─┌Ц│╬Ц│÷Ц─│Ц┐°Ц┐╪Ц┐╚Ц│▄Е▐█Е╞╬Ф√╧Е░▒Ц│╚Е⌡·Х╩╒Ц│≈Е╖▀Ц┌│Ц─│Х║²Г╙│Ц│╬Ц│╖Ц│╝И─╡Х║▄Ф√╧Е░▒Ц│╗Ц│╞И─├Ц│╚Х╥ЁЦ│╜Х©■Ц┌▀Е═╢Е░┬Ц┌┌Ц│┌Ц┌▀Ц─┌
Ц┐°Ц┐╪Ц┐╚Ц│╚Ц┐┬Ц┐┐Ц┐≈Ц┌╧Ц┐■Ц┐Ё Ц│▄Ц│▀Ц│▀Ц│ёЦ│╕Ц│└Ц┌▀Е═╢Е░┬Ц─│Д╦╕И─╡Ц│╚Ц┌┬Ц┌▀Ф▒╘Ф⌠╕Ц│╗Е⌡·Х╩╒Ц│╚Ц┌┬Ц┌▀Ф▒╘Ф⌠╕Ц│╝Д╫°Г■╗Ц│╞Е▐█Е╞╬Ф√╧Е░▒Ц│╖Ц│┌Ц┌▀Ц─┌Ц│⌠Ц│╝Е═╢Е░┬Ц│╝И│▀Е▀∙Ц│╞Ц─│2Ц│╓Ц│╝Ф┬░Е┬├Ц│╝Ц│╘Ц│║Ц┌┴Ц│▄Ф■╞И┘█Г └Ц│╖Ц│┌Ц┌▀Ц│▀Ц│╚Ц┌┬Ц│ёЦ│╕Ф╠╨Ц│╬Ц┌▀Ц─┌
Ц┐°Ц┐╪Ц┐╚Ц│▄Г╖╩Е▀∙Ц│≥Ц┌▀Ц│╝Ц│╚Ф╞■Ц│╧Ц│╞Ц┌▀Ц│▀Ц│╚И─÷Ц│▐Е⌡·Х╩╒Ц│≈Ц│╕Ц│└Ц┌▀Е═╢Е░┬Ц─│Е⌡·Х╩╒Ц│╚Ц┌┬Ц┌▀Ф▒╘Ф⌠╕Ц│▄Ф■╞И┘█Г └Ц│╚Ц│╙Ц┌▀Ц─┌Х║²Г╙│Е╬▄Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╝Х╖▓И─÷Е╨╕Ц│╞Ф╦⌡Е╟▒Ц│≈Ц─│Ф╟╢Е╧ЁФ√╧Е░▒Ц│╝И─÷Е╨╕Ц│╞Е╒≈Е┼═Ц│≥Ц┌▀Ц─┌Ц┐°Ц┐╪Ц┐╚Ц│╞Ц│²Ц┌▄Ц│╬Ц│╖Ц│╝И─╡Х║▄Ф√╧Е░▒Ц│╗Е░▄Ц│≤Е░▒Ц│█Ц│╚Ф┼╪Ц│≈Е┤╨Ц│∙Ц┌▄Ц┌▀Ц│▄Ц─│Ц┐░Ц┌╕Ц┐ЁЦ┐┴Ц│╝Ф°─И╚≤Г┌╧Ц│╞Д╫▌Ц│▐Ц│╙Ц┌┼Ц─│Е░▄Ц│≤Е░▒Ц│█Ц│╚Е⌡·Х╩╒Ц│≈Г╤ Ц│▒Ц┌▀Ц─┌
Ц┐°Ц┐╪Ц┐╚Ц│▄Е⌡·Х╩╒Ц│≥Ц┌▀Ц│╝Ц│╚Ф╞■Ц│╧Ц│╞Ц┌▀Ц│▀Ц│╚И─÷Ц│▐Е▀∙Ц│└Ц│╕Ц│└Ц┌▀Е═╢Е░┬Ц─│Д╦╕И─╡Ц│╚Ц┌┬Ц┌▀Ф▒╘Ф⌠╕Ц│▄Ф■╞И┘█Г └Ц│╚Ц│╙Ц┌▀Ц─┌Х║²Г╙│Е╬▄Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╝Х╖▓И─÷Е╨╕Ц│╞Е╒≈Е┼═Ц│≥Ц┌▀Ц┌┌Ц│╝Ц│╝Ц─│Ф╟╢Е╧ЁИ─÷Е╨╕Ц│╞Ф╦⌡Е╟▒Ц│≥Ц┌▀Ц─┌Ц┐°Ц┐╪Ц┐╚Ц│╝Ц┐░Ц┌╕Ц┐ЁЦ┐┴Ц│╞Ц│²Ц┌▄Ц│╬Ц│╖Ц│╝И╚≤Ц│∙Ц┌▓Х╤┘Ц│┬Ц┌▀Ц│⌠Ц│╗Ц│╞Ц│╙Ц│▐Ц─│Е░▄Ц│≤Ф√╧Е░▒Ц│╚Е⌡·Х╩╒Ц│≈Г╤ Ц│▒Ц┌▀Ц─┌ Е°╟И²╒Ц│▄Х╖▓Е╨╕н╦ Ц│═Ц│▒Е┌╬Ф√°Ц│≈Ц│╕Ц│└Ц┌▀Е═╢Е░┬Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╚Е┐█Ц│▐Е┼⌡Ц│╙Ц│╘Ц┌▓Е░╚Ц┌│Е┘╗Д╫⌠Ц│▄Х╖▓Е╨╕н╦ Ц│═Ц│▒Е⌡·Х╩╒Ц│≥Ц┌▀Ц│▄Ц─│И┤█Е┼⌡Ц│═Ц│▒Ц│╞Е╓┴Ц┌▐Ц┌┴Ц│ И┴⌡Г⌡╢Д╦▀Е░▒Ц│█Ц│╚Д╫°Г■╗Ц│≥Ц┌▀О╪┬Ц│≥Ц│╙Ц┌▐Ц│║Ц─│Е°╟И²╒Ц│╗Х╖▓Е╨╕н╦ Ц┌▓Ц│╙Ц│≥Ф√╧Е░▒О╪┴Ц─┌Ц│⌠Ц│╝Ц│╗Ц│█Ц─│И┤█Е┼⌡Ц│╞Е°╟И²╒Ц│╚Е╧ЁХ║▄Ц│╙Ф┬░Е┬├Ц┌▓Ф▄│Ц│╓Ц│÷Ц┌│Ц─│Ц│²Ц│╝Ф┬░Е┬├Ц│▄Ф▒╘Ф⌠╕Ц│╚Е╞└Д╦▌Ц│≈Ц┐°Ц┐╪Ц┐╚Ц│╝Е⌡·Х╩╒Ц│╚Ц┌┌Е╞└Д╦▌Ц│≥Ц┌▀[ 57]
Е█⌠Г░┐ Ц┌└Ц┐╘Ц┌╠Ц┐┐Ц┐┬Ц┐°Ц┐╪Ц┐╚ Ц│╙Ц│╘Ц│╝Ц┐╘Ц┌╠Ц┐┐Ц┐┬Ц┌╧Ц┐²Ц┐╪Ц┐└Ц│╚Ц│┼Ц│└Ц│╕Ц─│Г├÷Г╥╢Х─┘Ц│╞Ц┌╧Ц┐■Ц┐ЁО╪┬Ц┌╣Ц┌╓Ц┐┴Ц┌╧Ц┐■Ц┐ЁЦ┌▓Е░╚Ц┌─О╪┴Ц┌▓Е┬╘Г■╗Ц│≥Ц┌▀Ц│⌠Ц│╗Ц│╖Ц─│Е°╟И²╒Ц┌└Г⌡╦Ф┴▀Ц│╝Ц┐╘Ц┌╠Ц┐┐Ц┐┬ Ц│╗Ц│└Ц│ёЦ│÷Д╩√Ц│╝Г┴╘Д╫⌠Х║╗И²╒Ц│╚Ц┐°Ц┐╪Ц┐╚Ц│▄Е╫⌠Ц│÷Ц│ёЦ│÷И ⌡Ц│╚Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╝И─╡Х║▄Ф√╧Е░▒Ц│▄Г╙│Г└╤Е╓┴Ц┌▐Ц┌▀Ц┌┬Ц│├Ц│╚Ц│≥Ц┌▀Ц─┌Ц┌╞Ц┐╙Ц┌╠Ц┐┐Ц┐┬ Ц│╖Ц┌┌Е░▄Ф╖≤Ц│╚Ц─│Ц┐°Ц┐╪Ц┐╚Ц│▄Ц┐░Ц┌╕Ц┐ЁЦ┐┴Е°╟Г┌╧Ц│╖Е╓╖Ц│█Ц│▐Х╩▄И│⌠Е╓┴Е▄√Ц│≥Ц┌▀Ц┌┬Ц│├Ц│╙Ф┼∙ФЁ∙О╪┬Ц┌╧Ц┐■Ц┐ЁЦ┐°Ц┌╕Ц┐╙Ц┐ЁЦ┌╟О╪┴Ц│╝Ц│∙Ц│╬Ц│√Ц│╬Ц│╙Е╫╒Ф┘▀Ц│▄Е╜≤Е°╗Ц│≥Ц┌▀[ 60]
Х║²Г╙│Ф≥┌Ц│╚Ц┐╘Ц┌╟Ц┐⌠Ц┐╪Ц┐°Ц┐╪Ц┐╚Ц│╚Д╫°Г■╗Ц│≥Ц┌▀Е┼⌡Ц│╗Ц│≈Ц│╕Ц│╞Ц─│И┤█Е┼⌡ Ц─│Е·┌Г⌡╢Ф┼≈Е┼⌡ Ц─│Ф▒╘Ф⌠╕Е┼⌡ Ц│▄Ц│┌Ц┌▀Ц─┌ Ф╔∙Е├├Е╫╒Ц│╝Ц┐°Ц┐╪Ц┐╚О╪┬Ц┌╚Ц┐┼Ц┐┤Ц┌ёЦ┌╒Ц┐ЁЦ┐∙Ц┐┐Ц┐┬Ц┐°Ц┐╪Ц┐╚ Ц┌└Ц┐╘Ц┌╟Ц┐⌠Ц┐╪ Ц│╖Д╫©Г■╗Ц│∙Ц┌▄Ц┌▀Ц┌┌Ц│╝Ц│╙Ц│╘О╪┴Ц│╝Ц┐░Ц┌╕Ц┐ЁЦ┐┴Ц┌▓Д╨┬Ф╦╛Ц│≥Ц┌▀Ц│╝Ц│╞Ц─│Д╦─Х┬╛Ц│╚Г░┐Е╫╒Ц│╝Ц┐°Ц┐╪Ц┐╚Ц│╝Ц┐░Ц┌╕Ц┐ЁЦ┐┴Ц┌▓Д╨┬Ф╦╛Ц│≥Ц┌▀Ц┌┬Ц┌┼Ц┌┌Ц│╞Ц┌▀Ц│▀Ц│╚И⌡ёЦ│≈Ц│└Ц─┌Х║²Г╙│Ц│╝И ⌡Ц│╝Ц┐°Ц┐╪Ц┐╚Ц│╗Х║²Г╙│И²╒Ц│╝Ф▌╔Г┌╧Ц│╝Д╫█Г╫╝Ф╛║Г╛╛Ц│╖Ц─│Е·┌Г⌡╢Ф┼≈Е┼⌡ Ц│╞Ц┐°Ц┐╪Ц┐╚Ц│╝И┤█Е©┐ Ц│▀Ц┌┴Е┴█Е╬▄Ц│╚Ц│ Ц┌▄Ц│╕Д╫°Г■╗Ц│≥Ц┌▀Ц│⌠Ц│╗Ц┌┌Ц│┌Ц┌▀Ц│≈Ц─│Е°╟И²╒Ц│▀Ц┌┴Ц│╝Ф▒╘Ф⌠╕ Ц│╚Ц│╓Ц│└Ц│╕Ц┌┌Ц─│Ц┌╧Ц┐■Ц┐ЁЦ┌└Х║²Г╙│Ф≥┌Ц│╝И─÷Е╨╕Ц│═Ц│▒Ц│╖Ц│╞Ц│╙Ц│▐Ц┐°Ц┐╪Ц┐╚Ц│▄Ф▌╔Х╖╕Ц│≥Ц┌▀Д╫█Г╫╝Ц│╚Д╬²Е╜≤Ц│≥Ц┌▀Ц─┌Ц│╬Ц│÷Ц─│Ц┐°Ц┐╪Ц┐╚Ц│▄Е°╟И²╒Ц┌▓Х╩╒Ц│▄Ц┌▀Ц│╗Ц│█Ц─│Д╦─Х┬╛Ц│╚Е┼⌡Ц│╝Д╫°Г■╗Ц│≥Ц┌▀Г┌╧Ц│╞И┤█Е©┐Ц│╚Е╞╬Ц│≈Ц│╕Г⌡╦Е╞╬Г └Ц│╚Е╓┴Е▄√Ц│≥Ц┌▀Ц─┌Ц│²Ц│╝Ц│÷Ц┌│Ц─│Е·┌Г⌡╢Ф┼≈Е┼⌡Ц┌└И┤█Е┼⌡Ц┌▓Е░╚Ц┌─Ц│┌Ц┌┴Ц┌├Ц┌▀Ц┐°Ц┐╪Ц┐╚Ц│╚Ц│╞Ц│÷Ц┌┴Ц│▐Е┼⌡Ц│▄Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╚Ц┐┬Ц┐╚Ц┌╞ Ц┌▓Г■÷Ц│≤Ц┌▀Е▐╞Х┐╫Ф─╖Ц│▄Ц│┌Ц┌▀Ц─┌Ц│⌠Ц│╝Ц│⌠Ц│╗Ц│╚Ц┌┬Ц┌┼Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╞Х║²Г╙│Е╬▄Ц─│И─╡Х║▄Ф√╧Е░▒Ц│╝Е┴█Ф√╧Ц┌└Е╬▄Ф√╧Ц─│Ф╗╙Ф√╧Е░▒Ц│╙Ц│╘Ц─│Ц│┌Ц┌┴Ц┌├Ц┌▀Ф√╧Е░▒Ц│╚Ц┐░Ц┌╕Ц┐ЁЦ┐┴Ц│≥Ц┌▀Е▐╞Х┐╫Ф─╖Ц│▄Ц│┌Ц┌▀Ц─┌Е⌡·Х╩╒И│▀Е▀∙Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪Ц│╝Д╦─И┐╗Ц│▄Д╦╕И─╡И│▀Е▀∙Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪Ц│╚Е╓┴Ф▐⌡Ц│∙Ц┌▄Ц┌▀Е═╢Е░┬Ц┌┌Х─┐Ц│┬Ц┌┴Ц┌▄Ц┌▀Ц│▀Ц┌┴Ц─│Е▐█Г≥╨Д©┌Ф∙╟Ц│▄1Ц┌▓Х╤┘Ц│┬Ц┌▀Ц│⌠Ц│╗Ц┌┌Ц│┌Ц┌┼Ц─│Ц┐°Ц┐╪Ц┐╚Ц│╝И─╡Х║▄Ф√╧Е░▒Ц│╝И─÷Е╨╕Ц│▄Х║²Г╙│Д╩╔Е┴█Ц│╚Ф╞■Ц│╧Ц│╕Е╒≈Е┼═Ц│≥Ц┌▀Е═╢Е░┬Ц┌┌Ц│┌Ц┌▀[ 62]
Ц┐├Ц┐▀Ц┌╧Ц┐°Ц┐╪Ц┐╚ Ц┌▓Ц┐░Ц┌╧Ц┌╠Ц┐┐Ц┐┬Ц┐°Ц┐╪Ц┐╚ Ц│╝Д╦┼Ц│╚Д╧≈Ц│⌡Ц─│2Ц│╓Ц┌▓И┤█Ц│╜Ц│÷Ц│╬Ц│╬Е░▄Ф≥┌Ц│╚Е°╟И²╒Ц│╚Х░╫Д╦▀Ц│∙Ц│⌡Ц┌▀Ц│╗Ц─│Ц│²Ц│╝Ц┐├Ц┐▀Ц┌╧Ц┐°Ц┐╪Ц┐╚Ц│▄Х╥ЁЦ│╜Д╦┼Ц│▄Ц┌▀И╚≤Ц│∙Ц│╞Ц─│Ц┐├Ц┐▀Ц┌╧Ц┐°Ц┐╪Ц┐╚Ц┌▓Е█≤Г▀╛Ц│╖Х░╫Ц│╗Ц│≈Ц│÷Е═╢Е░┬Ц┌┬Ц┌┼Ц┌┌Ц│╞Ц┌▀Ц│▀Ц│╚И╚≤Ц│▐Ц│╙Ц┌▀[ 63] [ 64] Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪Д©²Е╜≤Е┴┤ Ц│╚Е▐█Ц│≈Ц│╕Ц│└Ц┌▀Ц┌┬Ц│├Ц│╚Х╕▀Ц│┬Ц┌▀[ 65] [ 63]
Ц┌┬Ц│▐Г■╗Ц│└Ц┌┴Ц┌▄Ц┌▀Х╙╛Ф≤▌Ц│╗Ц│≈Ц│╕Ц─│Ц│⌠Ц│╝Е∙▐И║▄Ц┌▓Ц┐░Ц┌╧Ц┌╠Ц┐┐Ц┐┬Ц┐°Ц┐╪Ц┐╚Ц│▄Е╨┼Ц│╚Х║²Г╙│Ц│≥Ц┌▀Ц│⌠Ц│╗Ц│╗Ц─│Ц┐░Ц┌╧Ц┌╠Ц┐┐Ц┐┬Ц┐°Ц┐╪Ц┐╚Ц│▄Ц┐├Ц┐▀Ц┌╧Ц┐°Ц┐╪Ц┐╚Ц│╚Х║²Г╙│Ц│≥Ц┌▀Ц│⌠Ц│╗Ц│╝2Ц│╓Ц│╚Е┬├Ц│▒Ц─│Ц│²Ц┌▄Ц│·Ц┌▄Ц│╝Е╫╠И÷©Ц┌▓Е┬╔Ц─┘Ц│╚Ф╓°Х╗▌Ц│≥Ц┌▀Ц┌┌Ц│╝Ц│▄Ц│┌Ц┌▀[ 63] [ 64] Е╝▄Е┘╗Е╪╬Ф─╖Х║²Г╙│ Ц┌▓Д╩╝Е╝ Ц│≥Ц┌▀Ц─┌Ц┐░Ц┌╧Ц┌╠Ц┐┐Ц┐┬Ц┐°Ц┐╪Ц┐╚Ц│▄1 m/sЦ│╖Е╨┼Ц│╚Х║²Г╙│Ц│≈Ц│÷Ц│╗Ц│█Ц─│Е░▄Ф╖≤Ц│╚1m/sЦ│╖Х╥ЁЦ│╜Х©■Ц┌▀Ц│⌠Ц│╗Ц│╚Ц│╙Ц┌▀Ц─┌Ц┐├Ц┐▀Ц┌╧Ц┐°Ц┐╪Ц┐╚Ц┌┌Е░▄Ф╖≤Ц│╚1 m/sЦ│╝И─÷Е╨╕Ц│╖Х░╫Д╦▀Ц│≥Ц┌▀Ц│▄Ц─│Ц┐░Ц┌╧Ц┌╠Ц┐┐Ц┐┬Ц┐°Ц┐╪Ц┐╚Ц┌▓Е÷╨Ф╨√Ц│╚Ц│≥Ц┌▀Ц│╗Ц┐░Ц┌╧Ц┌╠Ц┐┐Ц┐┬Ц┐°Ц┐╪Ц┐╚Ц│▄Е╨┼Ц│╚Х║²Г╙│Ц│≈Ц│╕Х╥ЁЦ│╜Х©■Ц│ёЦ│÷Е╬▄Ц│╞Ц─│Ц┐├Ц┐▀Ц┌╧Ц┐°Ц┐╪Ц┐╚Ц│╝Г⌡╦Е╞╬И─÷Е╨╕ Ц│╞2 m/sЦ│╗Ц│╙Ц┌▀Ц─┌Ц│≈Ц│÷Ц│▄Ц│ёЦ│╕Ц─│Ц┐├Ц┐▀Ц┌╧Ц┐°Ц┐╪Ц┐╚Ц│╞Ц┐░Ц┌╧Ц┌╠Ц┐┐Ц┐┬Ц┐°Ц┐╪Ц┐╚Ц│╚Е╞╬Ц│≈Ц│╕Г⌡╦Е╞╬И─÷Е╨╕2 m/sЦ│╖Х╥ЁЦ│╜Х©■Ц┌▀Ц│⌠Ц│╗Ц│╚Ц│╙Ц┌▀Ц─┌Ц│⌠Ц┌▄Ц│╞Е╨┼Ц│╚Е╞╬Ц│≥Ц┌▀И─÷Е╨╕Ц│╚Г⌡╢Ц│⌡Ц│╟3 m/sЦ│╖Ц│┌Ц┌▀Ц─┌Ц│╓Ц│╬Ц┌┼Ц─│Ц┐├Ц┐▀Ц┌╧Ц┐°Ц┐╪Ц┐╚Ц┌▓Е█≤Г▀╛Ц│╖Е╨┼Ц│╚Х░╫Д╦▀Ц│∙Ц│⌡Ц│÷Е═╢Е░┬Ц│╗Ф╞■Ц│╧Ц┌▀Ц│╗Ц─│3Е─█Ц│╝И─÷Е╨╕Ц│╖Х╥ЁЦ│╜Х©■Ц┌▀Ц│⌠Ц│╗Ц│╚Ц│╙Ц┌▀Ц─┌Ц│≈Ц│÷Ц│▄Ц│ёЦ│╕Ц─│Ц┐├Ц┐▀Ц┌╧Ц┐°Ц┐╪Ц┐╚Ц│╞Е█≤Г▀╛Ц│╝Е═╢Е░┬Ц│╗Ф╞■Х╪┐Ц│≈Ц│╕Ц─│9Е─█Ц│╝И╚≤Ц│∙Ц│╬Ц│╖Х╥ЁЦ│╜Х©■Ц┌▀[ ФЁ╗И┤┬ 4] И²·Е╪╬Ф─╖Х║²Г╙│ Ц│╖Ц│┌Ц┌▀Ц│▀Ц┌┴Ц─│Ц┐├Ц┐▀Ц┌╧Ц┐°Ц┐╪Ц┐╚Ц│▄Х╥ЁЦ│╜Х©■Ц┌▀И─÷Е╨╕Ц┌└Е┬╟И│■Ц│≥Ц┌▀Ф°─И╚≤И╚≤Е╨╕Ц│╞Д╦┼Х╗≤Ц│╝Г░├Х╚√Е─╓Ц┌┬Ц┌┼Ц┌┌Е╟▐Ц│∙Ц│▐Ц│╙Ц┌▀Ц│▄Ц─│Ц│²Ц┌▄Ц│╖Ц┌┌Е█≤Г▀╛Ц│╖Х░╫Д╦▀Ц│∙Ц│⌡Ц┌▀Е═╢Е░┬Ц┌┬Ц┌┼Ц┌┌И─÷Ц│▐Ц─│Ц┌┬Ц┌┼И╚≤Ц│▐Х╥ЁЦ│╜Х©■Ц┌▀Ц│╗Ц│└Ц│├Г╣░Х╚√Ц│╞Е╓┴Ц┌▐Ц┌┴Ц│╙Ц│└[ 64]
Ц│⌠Ц│╝Ц┌┬Ц│├Ц│╙И═├Ф╛║Х║²Г╙│Ц│▄Г≥╨Г■÷Ц│≥Ц┌▀Ц│╗Ц│└Ц│├Д╩╝Е╝ Ц│╞Е╝÷И ⌡Ц│╚Ц│╞Ф°┴Е┼╧Ц│╖Ц│╞Ц│╙Ц│└О╪┬Х║²Г╙│Ц│≈Ц│╕Х╥ЁЦ│╜Х©■Ц┌▀Ц│╬Ц│╖Ц│╝Ц│╩Ц│╗Ц┌⌠Ц│╘Ц│╝Ф≥┌И√⌠Ц│╚Ц│┼Ц│└Ц│╕Ц─│2Ц│╓Ц│╝Ц┐°Ц┐╪Ц┐╚Ц│╞Д╨▓Ц│└Ц│╚Ф▌╔Х╖╕Ц│≈Ц│÷Ц│╬Ц│╬Ц│╖Ц│┌Ц┌▀О╪┴Ц│▄Ц─│Ц│²Ц│├Ц│═Ц│╗Ц│≈Ц│╕Ц┌┌Ц│⌠Ц│╝Ц┐╒Ц┐┤Ц┐╚Ц│╞Е╝÷И╗⌠Г╣░Ф·°Ц┌▓Ц┌┬Ц│▐Е├█Г▐╬Ц│≥Ц┌▀Ц│⌠Ц│╗Ц│▄Г÷╔Ц┌┴Ц┌▄Ц│╕Ц│┼Ц┌┼[ 64] Х╤┘Ф√╟Ф≤÷ Ц│╝Ц┌ЁЦ┌╒Е╢╘Её┼ [Х╗ЁХ╙·Г√▒Е∙▐Г┌╧ Ц┌└Ц┌╧Ц┌╓Ц┐ЁЦ┌╟Ц┐░Ц┌╓ Г╜┴Ц│╝Ц┌┬Ц┌┼Х╓┤И⌡▒Ц│╙Г▐╬Х╠║Ц┌▓Г░├Х╖ёЦ│≥Ц┌▀Ц│÷Ц┌│Ц│╚Е┬╘Г■╗Ц│∙Ц┌▄Ц┌▀Ц│⌠Ц│╗Ц┌┌Ц│┌Ц┌▀[ 66]
Г░┐Ф┼─ Ц│╝Е⌡╫И ⌡Г╚╤Ф┼─И─ёГ⌡÷ Ц┌└Е░└Е⌡╫Ц│╝Е⌡╫Е├┘Г╚╤Ф┼─И─ёГ⌡÷ Ц│╞Ц─│Ц│∙Ц│╬Ц│√Ц│╬Ц│╙Ф√╧ФЁ∙Ц│╖Ц┐°Ц┐╪Ц┐╚Ц│╝Е╪╬Ц│©Е┘╥Е░┬Ц┌▓Х╕▐Е┬╤Ц│≈Ц│╕Ц│└Ц┌▀Ц─┌
AFL О╪ Ц┌╙Ц┐╪Ц┌╧Ц┐┬Ц┐╘Ц┐╙Ц┌╒Ц┐ЁЦ┐╩Ц┐∙Ц┐┐Ц┐┬Ц┐°Ц┐╪Ц┐╚ Ц│╖Г■╗Ц│└Ц┌┴Ц┌▄Ц┌▀Ц┐°Ц┐╪Ц┐╚Ц│╞Ц─│Ц│²Ц│╝Ц┌╡Ц┐╪Ц┌╦Е°╖ Ц┌▓[ 67] FIBA О╪ Ц┐░Ц┌╧Ц┌╠Ц┐┐Ц┐┬Ц┐°Ц┐╪Ц┐╚ Ц┌▓Ц┐°Ц┐╪Ц┐╚Ц│╝Д╦▀И┐╗Ц┌▓Е÷╨Ф╨√Ц│╗Ц│≈Ц│╕И╚≤Ц│∙1800 mmЦ│▀Ц┌┴Е╨┼Ц│╚Е░▒Ц│▒Ц│╕Х░╫Д╦▀Ц│∙Ц│⌡Ц┌▀Ц─┌Ц┐░Ц┌╕Ц┐ЁЦ┐┴Е╬▄Ц│╝Ф°─И╚≤И╚≤Е╨╕Ц│▄Ц┐°Ц┐╪Ц┐╚Ц│╝Д╦┼И┐╗Ц┌▓Е÷╨Ф╨√Ц│╗Ц│≈Ц│╕1200 mmЦ│▀Ц┌┴1400 mmЦ│╝Г╞└Е⌡╡Ц│╚Е▐▌Ц│╬Ц┌▀Ц┌┬Ц│├Ц│╚Ц─│Ц┌╡Ц┐╪Ц┌╦Е°╖Ц│▄Х╙©Ф∙╢Ц│∙Ц┌▄Ц┌▀[ 68] [ ФЁ╗И┤┬ 5] FIFA О╪ Ц┌╣Ц┐┐Ц┌╚Ц┐╪Ц┐°Ц┐╪Ц┐╚ Ц│╝Ц┌╡Ц┐╪Ц┌╦Е°╖Ц│╞Ц─│Ф╣╥Ф┼° 0 mЦ│╚Ц│┼Ц│└Ц│╕atm kPa О╪┴Ц│╝Г╞└Е⌡╡Ц│╚Е▐▌Ц│╬Ц┌▀Ц┌┬Ц│├Ц│╚Х╙©Ф∙╢Ц│∙Ц┌▄Ц┌▀[ 69] FIVB О╪ Ц┐░Ц┐╛Ц┐╪Ц┐°Ц┐╪Ц┐╚ Ц│╝Ц┌╡Ц┐╪Ц┌╦Е°╖Ц│╞Ц─│И─ Е╦╦Ц│╝Ц┐░Ц┐╛Ц┐╪Ц┐°Ц┐╪Ц┐╚Ц│╚Ц│┼Ц│└Ц│╕Ц│╞kgF /cm2 F /cm2 Ц┐⌠Ц┐╪Ц┐│Ц┐░Ц┐╛Ц┐╪ Ц│╚Ц│┼Ц│└Ц│╕Ц│╞kgF /cm2 F /cm2 [ 70] [ 71] ITF О╪ Ц─▄ХЁ╙И┤▐Ц│╝Е╓╖Ц│█Ц│└Ф╩▒Ц┌┴Ц│▀Ц│╖Е┴⌡Ф─╖Ц│╝Ц│┌Ц┌▀Ф╟╢Е╧ЁЦ│╙Ц┐√Ц┐╜Ц┐┐Ц┌╞Ц─█Ц│╚Ц┐├Ц┐▀Ц┌╧Ц┐°Ц┐╪Ц┐╚ Ц┌▓Х░╫Ц│╗Ц│≈Ц│÷Ф≥┌Ц│╝Ц─│Х╥ЁЦ│╜Х©■Ц┌▀И╚≤Ц│∙Ц┌▓Х╕▐Е┬╤Ц│≈Ц│╕Ц│└Ц┌▀Ц─┌ITTF О╪ Е█⌠Г░┐ Ц│╝Ц┐°Ц┐╪Ц┐╚Ц│╚Ц│╓Ц│└Ц│╕Ц─│30 cmЦ│╝И╚≤Ц│∙Ц│▀Ц┌┴Е█⌠Г░┐Е▐╟Ц│╚Х░╫Д╦▀Ц│∙Ц│⌡Ц│÷Ц│╗Ц│█Ц│╚Ц─│Г╢└23 cmЦ│╝И╚≤Ц│∙Ц│╬Ц│╖Х╥ЁЦ│╜Х©■Ц┌▀Ц┌┬Ц│├Ц│╚Ц─│Е█⌠Г░┐Е▐╟Ц│╝Х║╗И²╒Ц┌▓Х╙©Ф∙╢Ц│≥Ц┌▀Ц│⌠Ц│╗Ц│▄Х╕│Ф╠┌Ц│∙Ц┌▄Ц│╕Ц│└Ц┌▀[ 72] [ ФЁ╗И┤┬ 5] NBA О╪ Ц┐░Ц┌╧Ц┌╠Ц┐┐Ц┐┬Ц┐°Ц┐╪Ц┐╚ Ц│╝Ц┌╡Ц┐╪Ц┌╦Е°╖Ц│╞Ц─│7.5 psi Ц│▀Ц┌┴8.5 psiЦ│╝Г╞└Е⌡╡Ц│╚Е▐▌Ц│╬Ц┌▀Ц┌┬Ц│├Ц│╚Х╙©Ф∙╢Ц│∙Ц┌▄Ц┌▀О╪┬51.7Ц─°58.6 kPaО╪┴[ 73] NFL О╪ Ц┌╒Ц┐║Ц┐╙Ц┌╚Ц┐ЁЦ┐∙Ц┐┐Ц┐┬Ц┐°Ц┐╪Ц┐╚ Ц│╚Д╫©Ц┌▐Ц┌▄Ц┌▀Ц┐°Ц┐╪Ц┐╚Ц│╝Ц┌╡Ц┐╪Ц┌╦Е°╖Ц│╞Ц─│12.5 psiЦ│▀Ц┌┴13.5 psiЦ│╝Г╞└Е⌡╡Ц│╚Е▐▌Ц│╬Ц┌▀Ц┌┬Ц│├Х╙©Ф∙╢Ц│∙Ц┌▄Ц┌▀О╪┬86Ц─°93 kPaО╪┴[ 74] RО╪├A / USGA О╪ Ц┌╢Ц┐╚Ц┐∙Ц┐°Ц┐╪Ц┐╚Ц│╝Е▐█Г≥╨Д©┌Ф∙╟Ц│²Ц│╝Ц┌┌Ц│╝Ц│╚Е╞╬Ц│≈Ц│╕Е┬╤И≥░Ц│▄Х╙╡Ц│∙Ц┌▄Ц│╕Ц│└Ц┌▀Ц─┌Ц┌╢Ц┐╚Ц┐∙Ц┌╞Ц┐╘Ц┐√ Ц│╚Е╞╬Ц│≈Ц│╕0.83Ц┌▓Х╤┘Ц│┬Ц┌▀Е▐█Г≥╨Д©┌Ф∙╟Ц│╚Ц│╙Ц┌▀Ц┌┬Ц│├Ц│╙Ц┐°Ц┐╪Ц┐╚Ц│╞Х╗╠Е▐╞Ц│∙Ц┌▄Ц│╙Ц│└[ 75] Ц┌╒Ц┐║Ц┐╙Ц┌╚Ц┐ЁЦ┐∙Ц┐┐Ц┐┬Ц┐°Ц┐╪Ц┐╚Ц│╚Ц│┼Ц│▒Ц┌▀Ц┐┤Ц┐∙Ц┐╛Ц┐╪Ц┐┬Ц┌╡Ц┐╪Ц┐┬Е∙▐И║▄ О╪┬Х▀╠Х╙·Г┴┬ О╪┴ [ 76] [ 77] И┤▌Г░┐ Ц│╖Ц│╞Ц─│1900Е╧╢Ц│■Ц┌█Ц│▀Ц┌┴Ф┴⌠Х─┘Д╦█Е┬╘Ц│╝Г┼╤ФЁ│Ц│▄И∙╥Ц┌┴Ц│▐Г╤ Ц│└Ц│╕Ц│└Ц│÷О╪┬Ц┐┤Ц┐┐Ц┐┴Ц┐°Ц┐╪Ц┐╚Ф≥┌Д╩ё О╪┴Ц│▄Ц─│Ц┌ЁЦ┐╚Ц┌╞Ц┌▓Х┼╞Ц│╚Г■╗Ц│└Ц│÷Ц┐°Ц┐╪Ц┐╚Ц│▄Е╟▌Е┘╔Ц│∙Ц┌▄Ц│÷Ц│⌠Ц│╗Ц┌└Ц┌╧Ц┐■Ц┐┐Ц┐┬Ц┐°Ц┐╪Ц┐╚Ц│▄Г╕│Ф╜╒Ц│∙Ц┌▄Ц│÷Ц│⌠Ц│╗Ц┌▓Ц│█Ц│ёЦ│▀Ц│▒Ц│╚Ц─│Ц┐╘Ц┌╓Ц┐√Ц┐°Ц┐╪Ц┐╚Ф≥┌Д╩ё Ц│╗Е▒╪Ц│╟Ц┌▄Ц┌▀Ф┴⌠Х─┘Ц│╚Ф°┴Е┬╘Ц│╙Ф≥┌Д╩ёЦ┌▓Х©▌Ц│┬Ц┌▀Ц│⌠Ц│╗Ц│╗Ц│╙Ц│ёЦ│÷[ 78] [ 79] [ 80]
^ Е°╟Г░┐Д╦┼Ц│╚Ц│┼Ц│▒Ц┌▀И┤█Е┼⌡Ц│╞Ц─│Г┴╘Д╫⌠Ц│╗Е°╟Г░┐Ц│▄Е╪∙Ц│█Е░┬Ц│├Д╦┤Ф°┴Е╪∙Е┼⌡Ц│╗Ц─│Е°╟Г░┐Ц│╝Х┤╙Х╩╒Ц│╚Ц┌┬Ц│ёЦ│╕Г┴╘Д╫⌠Ц│╚Ц│▀Ц│▀Ц┌▀И│═Е©┐Е┼⌡Ц│╝Е░┬Е┼⌡Ц│╗Ц│≈Ц│╕Е╝ Г╬╘Ц│∙Ц┌▄Ц┌▀Ц─┌Е╬⌠Ц│ёЦ│╕Ц─│Х┤╙Х╩╒Х╩╦Ц│▀Ц┌┴Ц│╝Х╥²И⌡╒Ц│▄И│═Ц│└Д╫▌Г╥╞Е╨╕Е°╟Е╦╞Ц│╩Ц│╘И┤█Е┼⌡Ц│╞Е╟▐Ц│∙Ц│▐Ц│╙Ц┌▀[ 8] [ 9] [ 10] [ 8]
^ Ф╜ёГ╒╨Ц│╚Ц│╞Ц─│И╚≤Е╨╕Ц│▄Е┬²Ф°÷Е─╓Ц│╖Ц│┌Ц┌▀y 0 Ц│╚Ф┬╩Ц┌▀Ц│╬Ц│╖
^ Ц│⌠Ц│⌠Ц│╖Ц─│v Ц│╗u Ц│╞Ц┐°Ц┐╪Ц┐╚Ц┌└Г┴╘Д╫⌠Х║╗И²╒Ц│╝И─÷Ц│∙Ц│╖Ц│╞Ц│╙Ц│▐Ц─│И─÷Е╨╕Ц┌▓Х║╗Ц│≈Ц│╕Ц│└Ц┌▀Ц─┌Ц│╓Ц│╬Ц┌┼Ц─│Е╓╖Ц│█Ц│∙Ц│═Ц│▒Ц│╖Ц│╙Ц│▐Ц│²Ц│╝Е░▒Ц│█(Г╛╕Е▐╥ )Ц┌┌Е░╚Ц┌⌠Ц│╖Ц│└Ц┌▀Ц─┌
^ Е┼⌡Е╜╕Г └Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪Д©²Е╜≤Ц│╝ФЁ∙Е┴┤Ц│╞
1
2
m
v
f
2
=
m
g
H
f
{\displaystyle \textstyle {\frac {1}{2}}mv_{\text{f}}^{2}=mgH_{\text{f}}}
H
f
{\displaystyle \textstyle H_{\text{f}}}
v
f
2
{\displaystyle v_{\text{f}}^{2}}
^ a b
e
=
H
f
H
i
{\displaystyle \textstyle e={\sqrt {\frac {H_{\text{f}}}{H_{\text{i}}}}}}
^ Е║ Ф°╛ Ф╣╘Е▐╦ (2018). Б─°Е╪╬Ф─╖Ц┐╩И²·Е╪╬Ф─╖Ц┐°Ц┐╪Ц┐╚Ц│╝Е┼⌡Е╜╕Ц┐╒Ц┐┤Ц┐╚ : Е┼⌡Е╜╕Е┘╔И√─Ф∙≥Ф²░И√▀Г≥╨Ц│╝Е÷╨Г╓▌Ц│╗Ц│≈Ц│╕Б─² . Е█┐Х▒┴Г╖▒Е╜╕Е╓╖Е╜╕Г╢─Х╕│ (Е█┐Х▒┴Г╖▒Е╜╕Е╓╖Е╜╕) (11): 91-99. ISSN 1882-3505 . http://id.nii.ac.jp/1222/00000242/ . ^
Whittington, E. M., ed (2001). The Sport of Life and Death: The Mesoamerican Ballgame Thames & Hudson . ISBN 0-500-05108-9 . https://archive.org/details/sportoflifedeath00emic
^ a b
Brancazio, P. J. (1985). Б─°Trajectory of a fly ballБ─². The Physics Teacher 23 (1): 20Б─⌠23. Bibcode : 1985PhTea..23...20B . doi :10.1119/1.2341702 .
^
Walker, J. (2014). Fundamentals of Physics (10th Extended ed.). John Wiley & Sons . Figure 4-8, p. 70. ISBN 978-1-118-23072-5
^ Liu, Vi-Cheng (1957-01-01). Б─°On the motion of a projectile in the atmosphereБ─² (Х▀╠Х╙·). Zeitschrift fц╪r angewandte Mathematik und Physik ZAMP 8 (1): 76Б─⌠82. doi :10.1007/BF01601158 . ISSN 1420-9039 . https://doi.org/10.1007/BF01601158 . ^ a b
Bush, J. W. M. (2013). Б─°The aerodynamics of the beautiful gameБ─² . In Clanet, C.. Sports Physics . Les ц┴ditions de l'ц┴cole Polytechnique . p. 171. hdl :1721.1/87576 ISBN 978-2-7302-1615-9 . https://bloximages.newyork1.vip.townnews.com/statesville.com/content/tncms/assets/v3/editorial/7/07/7077f0fa-f415-11e4-8ffc-03cf21769235/554a4fa5e09e9.pdf.pdf
^
Hirt, C.; Claessens, S.; Fecher, T.; Kuhn, M.; Pail, R.; Rexer, M. (2013). Б─°New ultrahigh-resolution picture of Earth's gravity fieldБ─². Geophysical Research Letters 40 (16): 4279Б─⌠4283. Bibcode : 2013GeoRL..40.4279H . doi :10.1002/grl.50838 .
^ a b Б─°Е°╟Д╦┼И┤█Е┼⌡Ф╦╛И┤▐ Б─². www.gsi.go.jp . Е⌡╫Е°÷Е°╟Г░├И≥╒. 2021Е╧╢3Ф°┬5Ф≈╔И√╡Х╕╖Ц─┌
^ Д╦┴Ф╣╕ Х▀╠Д©┼ (2015). Б─°Г╥╞Е╨╕Г╣▄Е╨╕Ц┌▓Г■╗Ц│└Ц│÷3Ц│╓Ц│╝Х╥²И⌡╒Х╗┬Г╝≈Ф√╧ФЁ∙Б─². Ц┌╙Ц┐ Ц┐╛Ц┐╪Ц┌╥Ц┐╖Ц┐ЁЦ┌╨Ц┐╩Ц┐╙Ц┌╣Ц┐╪Ц┐│ 60 (12): 701-705. ISSN 0030-3674 . ^ Б─°WebЦ┐├Ц┌╜Ц┌╧Ц┐┬Ф╦╛Е°╟Е╜╕ 2-2.И┤█Е┼⌡ Б─². Ф≈╔Ф°╛Ф╦╛Е°╟Е╜╕Д╪ . 2021Е╧╢3Ф°┬22Ф≈╔И√╡Х╕╖Ц─┌ ^ Е╠╠Г■╟ Г⌡⌡Е╓╚ (1971). Б─°Е┼⌡Е╜╕Г └Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪Ц│╗Ц│²Ц│╝Д©²Е╜≤Ф─╖Б─². Г┴╘Г░├Ф∙≥Х┌╡ 19 (2): 92-100. doi :10.20653/pesj.19.2_92 . ISSN 2432-1028 . ^ Richmond, Opoku-Sarkodie; Edward, Acheampong (4 2015). Б─°Vector-Valued Function Application to Projectile MotionБ─². Asia Pacific Journal of Education, Arts and Sciences 2 (2): 92-104. ISSN 2362-8030 . ^ a b
Nave, R.. Б─°Trajectories Б─². HyperPhysics
^ Е╝╝Е╣°, Ф╜╕Ц─│Е╝┬, Хё∙Д╧÷Ц─▄Х╨╚Х©▒Ц│╙Ц│╙Ц│▄Ц┌▄Ц│╝Е┬╤Е╬║ Ц─█О╪┬pdfО╪┴Ц─▌Ц│╙Ц│▄Ц┌▄Ц─▐Г╛╛38Е╥╩Г╛╛6Е▐╥Ц─│2019Е╧╢Ц─│443-448И═│Ц─│2021Е╧╢3Ф°┬18Ф≈╔И√╡Х╕╖ Ц─┌ ^
Б─°Dry air properties Б─². The Engineering Toolbox
^
Southard, J. (Fall 2006). Б─°Chapter 3: Flow past a sphere II: Stoke's law, the Bernoulli equation, turbulence, boundary layers, flow separationБ─² . Special Topics: An Introduction to Fluid Motions, Sediment Transport, and Current-generated Sedimentary Structures MIT . pp. 35Б─⌠82. Ц┌╙Ц┐╙Ц┌╦Ц┐┼Ц┐╚Ц│╝2017-02-05Ф≥┌Г┌╧Ц│╚Ц│┼Ц│▒Ц┌▀Ц┌╒Ц┐╪Ц┌╚Ц┌╓Ц┐√Ц─┌. https://ocw.mit.edu/courses/earth-atmospheric-and-planetary-sciences/12-090-special-topics-an-introduction-to-fluid-motions-sediment-transport-and-current-generated-sedimentary-structures-fall-2006/lecture-notes/ch3.pdf
^
Metha, R. D. (2008). Б─°Sports ball aerodynamicsБ─². In Nц╦rstrud, H.. Sport Aerodynamics . CISM International Centre for Mechanical Sciences. 506 . Springer . pp. 229Б─⌠331. doi :10.1007/978-3-211-89297-8_12 . ISBN 978-3-211-89296-1
^
Б─°Drag of a sphere Б─². NASA . 2021Е╧╢3Ф°┬22Ф≈╔И√╡Х╕╖Ц─┌
^ Ф╦┘Ф╟╢ Е╧╦Д╦╦ (1990). Б─°И╒╗Ц│╝И│┼Ц│Ё/Ц┌╕Ц┌ёЦ┐ЁЦ┐┴Ц┐╩Ц┐⌠Ц┌╦Ц┐█Ц┌╧ Б─°И╒╗Ц│╝И│┼Ц│ЁЕ╥╔Е╜╕Д╨▀Е┘╦Б─² Ц│╚Ц│╓Ц│└Ц│╕Б─². И╒╗Е┼⌡Ц┌╗Ц┐█Ц┐╚Ц┌╝Ц┐╪Е┬╘Г■╗Ц┌╥Ц┐ЁЦ┐²Ц┌╦Ц┌╕Ц┐═ 12 : 61-74. doi :10.11333/jweasympo1979.12.61 . ^
Б─°Ideal lift of a spinning ball Б─². NASA . 2017Е╧╢2Ф°┬2Ф≈╔И√╡Х╕╖Ц─┌
^ a b MARUYAMA, Yuichi (2009). Б─°Study on Physical Mechanism of the Magnus EffectБ─² . JOURNAL OF THE JAPAN SOCIETY FOR AERONAUTICAL AND SPACE SCIENCES 57 (667): 309Б─⌠316. doi :10.2322/jjsass.57.309 . ISSN 1344-6460 . https://doi.org/10.2322/jjsass.57.309 .
^ Г■╟Д╦╜Ф≥┐Е╧ЁЦ┐╩Г╕▐И┤█Х╡╢Д╧▀Ц┐╩Е╝╝Е╣°Ц──Ф╜╕Ц┐╩Е╖╚И┤▌И╬█Е╓╙И┐▌ (2014). Б─°Е█⌠Г░┐Ц┐°Ц┐╪Ц┐╚Ц│╝Г╘╨Е┼⌡Г┴╧Ф─╖Б─². Ц│╙Ц│▄Ц┌▄ 33 (1). ^ a b
Nathan, A. M. (2008). Б─°The effect of spin on the flight of a baseballБ─² . American Journal of Physics 76 (2): 119Б─⌠124. arXiv :physics/0605041 . Bibcode : 2008AmJPh..76..119N . doi :10.1119/1.2805242 . http://baseball.physics.illinois.edu/AJPFeb08.pdf .
^
Kim, J.; Park, H.; Choi, H.; Yoo, J. Y. (2011). Б─°Inverse Magnus effect on a rotating sphereБ─² (PDF) . 64th Annual Meeting of the APS Division of Fluid Dynamics . American Physical Society . Bibcode :2011APS..DFD.A7008K .
^
Kim, J.; Choi, H.; Park, H.; Yoo, J. Y. (2014). Б─°Inverse Magnus effect on a rotating sphere: When and whyБ─². Journal of Fluid Mechanics 754 : R2. Bibcode : 2014JFM...754R...2K . doi :10.1017/jfm.2014.428 .
^
Б─°Magnus effect Б─². HumanKinetics.com (2008Е╧╢11Ф°┬11Ф≈╔). 2017Е╧╢1Ф°┬27Ф≈╔И√╡Х╕╖Ц─┌
^ DeForest, C. (1997Е╧╢). Б─°Why are golf balls dimpled? Б─². The Original Usenet Physics FAQ . 2019Е╧╢7Ф°┬23Ф≈╔Ф≥┌Г┌╧Ц│╝Ц┌╙Ц┐╙Ц┌╦Ц┐┼Ц┐╚ Ц┌┬Ц┌┼Ц┌╒Ц┐╪Ц┌╚Ц┌╓Ц┐√Ц─┌2017Е╧╢1Ф°┬27Ф≈╔И√╡Х╕╖Ц─┌ ^
Clanet, C. (2015). Б─°Sports ballisticsБ─² . Annual Review of Fluid Mechanics 47 : 455Б─⌠478. Bibcode : 2015AnRFM..47..455C . doi :10.1146/annurev-fluid-010313-141255 . http://baseball.physics.illinois.edu/clanet/ClanetSportsBallistics.pdf .
^
Б─°Inzamam charged by ICC Б─². The Guardian
^
Okrent, D.; Wulf, S. (1989). Baseball anecdotes Oxford University Press . p. 89. ISBN 978-0-19-504396-9 . https://books.google.com/books?id=t3RjFXcgXzEC&q=spitball
^ Ф≈╔Ф°╛И┤▌Г░┐Х╕▐Е┴┤Е╖■Е⌠║Д╪ (2012Е╧╢1Ф°┬25Ф≈╔). Б─°Д╨▄Ц─┤Д╦─Д╨▄Е╧╢Е╨╕Ц──И┤▌Г░┐Х╕▐Е┴┤Ф■╧Ф╜ё Б─² (PDF). Ф≈╔Ф°╛И┤▌Г░┐Ф╘÷Ф╖▀. 2021Е╧╢3Ф°┬18Ф≈╔И√╡Х╕╖Ц─┌ ^ Е├┘Г■╟ Г⌡╢ (1992). Б─°Х┤╙Г■╠Х░╫Д╦▀И│▀Е▀∙Ц│╝Ф╦╛Е╝ Б─² . Ф²╠Д╨╛Е╝╤Ф■©Е╓╖Е╜╕Г═■Г╘╤Г╢─Х╕│ 2 Х┤╙Г└╤Г╖▒Е╜╕ (Ф²╠Д╨╛Е╝╤Ф■©Е╓╖Е╜╕) 32 : 15-19. ISSN 03851214 . http://id.nii.ac.jp/1653/00010493/ 2021Е╧╢3Ф°┬8Ф≈╔И√╡Х╕╖Ц─┌ . ^ a b
Cross, R. (1999). Б─°The bounce of a ballБ─² . American Journal of Physics 67 (3): 222Б─⌠227. Bibcode : 1999AmJPh..67..222C . doi :10.1119/1.19229 . http://www.physics.usyd.edu.au/~cross/PUBLICATIONS/5.%20BallBounce.pdf .
^ a b c d e f g
Georgallas, A.; Landry, G. (2016). Б─°The coefficient of restitution of pressurized balls: A mechanistic modelБ─² . Canadian Journal of Physics 94 (1): 42. Bibcode : 2016CaJPh..94...42G . doi :10.1139/cjp-2015-0378 . hdl :1807/69855 . https://www.researchgate.net/publication/281791329 .
^ Ф²╬Е╢▌ Е│╔ (1992). Б─°Х╖▓И│▀Е▀∙И┤▐Ц┌▓Ф▄│Ц│ёЦ│÷Х░╫Д╦▀Г░┐Д╫⌠Ц│╝Х╥ЁЦ│╜Х©■Ц┌┼Ц│╚И√╒Ц│≥Ц┌▀Е╝÷И╗⌠Г └Г═■Г╘╤Б─². Г═┌И≤╡Е╜╕Д╪ Х╙▄ 45 (2): 12-17. doi :10.11475/sabo1973.45.2_12 . ^
Б─°Coefficient of restitution Б─². RacquetResearch.com . 2016Е╧╢11Ф°┬23Ф≈╔Ф≥┌Г┌╧Ц│╝Ц┌╙Ц┐╙Ц┌╦Ц┐┼Ц┐╚ Ц┌┬Ц┌┼Ц┌╒Ц┐╪Ц┌╚Ц┌╓Ц┐√Ц─┌2017Е╧╢1Ф°┬27Ф≈╔И√╡Х╕╖Ц─┌
^ NASU, Hideaki; KAGAWA, Hiroyuki; TAKAHASHI, Masaya; YONEYAMA, Takeshi; IGARASHI, Shigeto; SATO, Kazutaka (2005). Б─°S3 Development of an Evaluation System for Coefficient of Restitution on Metal Baseball BatБ─² . The Proceedings of Joint Symposium: Symposium on Sports Engineering, Symposium on Human Dynamics 2005 (0): 9Б─⌠13. doi :10.1299/jsmesports.2005.0_9 . ISSN 2433-1309 . https://doi.org/10.1299/jsmesports.2005.0_9 . ^ Е°▀Д╩╡Е╞⌡Д╨╨Ц─▄Е╥╗Х╕√Г └Г┴╘Д╫⌠Ц│╝И²·Е╪╬Ф─╖Х║²Г╙│ Ц─█Ц─▌Г┴╘Ф─╖Г═■Г╘╤Ц─▐Г╛╛90Е╥╩Г╛╛5Е▐╥Ц─│Г┴╘Ф─╖Г═■Г╘╤Е┬┼Х║▄Д╪ Ц─│2008Е╧╢8Ф°┬Ц─│685-720И═│Ц─│ISSN 05252997 Ц─│NAID 110006873979 Ц─┌ ^ И╞√Г■╟Г╖─Ф╗╧Ц─▄Е▐█Г≥╨Д©┌Ф∙╟Ц│╗Е╓┴Ф▐⌡Х║▄Е┬≈Ц│╝Х║▄Е┬≈Е╪▐(Е╞└Ф⌡╦) Ц─█Ц─▌Г┴╘Г░├Ф∙≥Х┌╡Ц─▐Г╛╛35Е╥╩Г╛╛3Е▐╥Ц─│Ф≈╔Ф°╛Г┴╘Г░├Ф∙≥Х┌╡Е╜╕Д╪ Ц─│1987Е╧╢Ц─│179-180И═│Ц─│doi :10.20653/pesj.35.3_179 Ц─│ISSN 0385-6992 Ц─│NAID 110007489641 Ц─┌ ^ a b
Haron, A.; Ismail, K. A. (2012). Б─°Coefficient of restitution of sports balls: A normal drop testБ─². IOP Conference Series: Materials Science and Engineering 36 (1): 012038. Bibcode : 2012MS&E...36a2038H . doi :10.1088/1757-899X/36/1/012038 .
^ a b
Cross, R. (2000). Б─°The coefficient of restitution for collisions of happy balls, unhappy balls, and tennis ballsБ─² . American Journal of Physics 68 (11): 1025Б─⌠1031. Bibcode : 2000AmJPh..68.1025C . doi :10.1119/1.1285945 . http://www.physics.usyd.edu.au/~cross/PUBLICATIONS/12.%20Unhappy.PDF .
^
Cross, R. (2002). Б─°Grip-slip behavior of a bouncing ballБ─² . American Journal of Physics 70 (11): 1093Б─⌠1102. Bibcode : 2002AmJPh..70.1093C . doi :10.1119/1.1507792 . http://www.physics.usyd.edu.au/~cross/Gripslip.pdf .
^ a b
Zhang, X.; Vu-Quoc, L. (2002). Б─°Modeling the dependence of the coefficient of restitution on the impact velocity in elasto-plastic collisionsБ─². International Journal of Impact Engineering 27 (3): 317Б─⌠341. doi :10.1016/S0734-743X(01)00052-5 .
^
Hesser-Knoll, M. (2014Е╧╢). Б─°Ball spin during bounce Б─². The Physics of Tennis . University of Alaska Fairbanks . 2017Е╧╢2Ф°┬1Ф≈╔И√╡Х╕╖Ц─┌
^
Б─°Follow the bouncing ball Б─². Tennis Industry (2004Е╧╢4Ф°┬). 2017Е╧╢2Ф°┬1Ф≈╔И√╡Х╕╖Ц─┌
^
Allen, T.; Haake, S.; Goodwill, S. (2010). Б─°Effect of friction on tennis ball impactsБ─². Proceedings of the Institution of Mechanical Engineers, Part P 224 (3): 229Б─⌠236. doi :10.1243/17543371JSET66 .
^ a b c
Cross, R. (2005). Б─°Bounce of a spinning ball near normal incidenceБ─² . American Journal of Physics 73 (10): 914Б─⌠920. Bibcode : 2005AmJPh..73..914C . doi :10.1119/1.2008299 . http://www.physics.usyd.edu.au/~cross/PUBLICATIONS/31.%20Spin.pdf .
^
Allen, T. (2012). Б─°The ball's in your courtБ─² . ANSYS Advantage Ц┌╙Ц┐╙Ц┌╦Ц┐┼Ц┐╚ Ц│╝2017-02-05Ф≥┌Г┌╧Ц│╚Ц│┼Ц│▒Ц┌▀Ц┌╒Ц┐╪Ц┌╚Ц┌╓Ц┐√Ц─┌. https://web.archive.org/web/20170205013757/http://resource.ansys.com/staticassets/ANSYS/staticassets/resourcelibrary/article/AA-V6-I2-The-Balls-in-Your-Court.pdf .
^
Jafri, S. M. M. (2004). Modeling of impact dynamics of a tennis ball with a flat surface (PDF) (Thesis). Texas A&M University . hdl :1969.1/2441
^ Vaibhav Ghiya (2015) (Х▀╠Х╙·). Aerodynamics of cricket ball swing: An overview doi :10.13140/RG.2.1.1676.7523 . http://rgdoi.net/10.13140/RG.2.1.1676.7523 . ^
Cross, R. (2011). Б─°Bounce of an oval shaped footballБ─² . Sports Technology 3 (3): 168Б─⌠180. doi :10.1080/19346182.2011.564283 . http://www.physics.usyd.edu.au/~cross/FootballBounce.pdf .
^ a b c
Huebner, J. S.; Smith, T. L. (1992). Б─°Multi-ball collisionsБ─² . The Physics Teacher 30 (1): 46. Bibcode : 1992PhTea..30...46H . doi :10.1119/1.2343467 . https://works.bepress.com/jay_huebner/3/download/ .
^ a b c d
Cross, R. (2007). Б─°Vertical bounce of two vertically aligned ballsБ─² . American Journal of Physics 75 (11): 1009Б─⌠1016. Bibcode : 2007AmJPh..75.1009C . doi :10.1119/1.2772286 . http://www.physics.usyd.edu.au/~cross/PUBLICATIONS/38.%202BallBounce.pdf .
^
Harter, W. G. (1971). Б─°Velocity amplification in collision experiments involving superballsБ─² . American Journal of Physics 39 (6): 656Б─⌠663. Bibcode : 1971AmJPh..39..656H . doi :10.1119/1.1986253 . http://www.uark.edu/ua/modphys/pdfs/Journal_Pdfs/Velocity_Amplification_in_Collision_Experiments_Involving_Superballs-Harter-1971.pdf .
^
Nave, R.. Б─°Double ball drop Б─². HyperPhysics
^
Laws of Australian Football 2017 AFL . (2017). p. 15. http://www.aflcommunityclub.com.au/fileadmin/user_upload/Coach_AFL/2017_Laws_of_Australian_Football.pdf 2018Е╧╢1Ф°┬19Ф≈╔И√╡Х╕╖Ц─┌
^
Official Basketball Rules 2014 Basketball Equipment FIBA . (2014). p. 12. http://www.fiba.com/downloads/Rules/2014/BasketballEquipment2014_Final_V1_withCovers_LOW.pdf
^
Laws of the Game: 2014Б─⌠15 FIFA . (2014). p. 15. http://www.canadasoccer.com/files/2014_15_Laws_of_The_Game_EN.pdf
^
Official Volleyball Rules: 2017Б─⌠2020 FIVB . (2016). p. 16. https://www.fivb.org/EN/Refereeing-Rules/documents/FIVB-Volleyball_Rules_2017-2020-EN-v06.pdf
^
Official Beach Volleyball Rules: 2017Б─⌠2020 FIVB . (2017). p. 15. https://www.fivb.org/EN/Refereeing-Rules/Documents/FIVB-BeachVolleyball_Rules_2017-2020-EN-v05.pdf
^ The International Table Tennis Federation Handbook ITTF . (2017). p. 24. Ц┌╙Ц┐╙Ц┌╦Ц┐┼Ц┐╚ Ц│╝2018-04-24Ф≥┌Г┌╧Ц│╚Ц│┼Ц│▒Ц┌▀Ц┌╒Ц┐╪Ц┌╚Ц┌╓Ц┐√Ц─┌. https://web.archive.org/web/20180424162823/http://d3mjm6zw6cr45s.cloudfront.net/2016/12/2017_ITTF_Handbook.pdf 2017Е╧╢10Ф°┬20Ф≈╔И√╡Х╕╖Ц─┌ ^
Official Rules of the National Basketball Association: 2013Б─⌠2014 NBA . (2013). p. 10. http://www.nba.com/media/dleague/1314-nba-rule-book.pdf
^
Official Playing Rules of the National Football League NFL . (2016). p. 3. http://edge-operations.nfl.com/media/2224/2016-nfl-rulebook.pdf
^
Rubenstein, L. (2002Е╧╢5Ф°┬11Ф≈╔). Б─°Getting to COR of game, finallyБ─² . https://www.theglobeandmail.com/sports/golf/getting-to-cor-of-game-finally/article754694/ 2017Е╧╢1Ф°┬27Ф≈╔И√╡Х╕╖Ц─┌
^
Б─°'Deflategate:' 4-game suspension for Tom Brady Б─². CNN (2015Е╧╢5Ф°┬11Ф≈╔). 2017Е╧╢1Ф°┬27Ф≈╔И√╡Х╕╖Ц─┌
^
Well, Jr., T. V.; Karp, B. S.; Reisner, L. L. (2015). Investigative Report Concerning Footballs Used During the AFC Championship Game on January 18, 2015 Paul, Weiss, Rifkind, Wharton & Garrison LLP . https://nfllabor.files.wordpress.com/2015/05/investigative-and-expert-reports-re-footballs-used-during-afc-championsh.pdf
^ Mitchell T. Woltring (2018). Б─°Examining Perceptions of BaseballБ─≥s Eras: A Statistical ComparisonБ─². Sport Journal . ^
Б─°Evolution of the ballБ─². Baseball Digest
^
Sowell, T. (2011). Б─°Dead ball vs lively ballБ─² . The Thomas Sowell Reader . Basic Books . ISBN 9780465022502 . https://books.google.com/books?id=hxmQ2W-yGiwC&pg=PA62
Post, S. (2010). Applied and computational fluid mechanics Jones and Bartlett Publishers . pp. 280Б─⌠282. ISBN 978-1-934015-47-6 . https://books.google.com/books?id=Y8e4q-BZIqYC&pg=PA280 Cross, R.; Nathan, A. M. (2006). Б─°Scattering of a baseball by a batБ─². American Journal of Physics 74 (10): 896Б─⌠904. arXiv :physics/0605040 . Bibcode : 2006AmJPh..74..896C . doi :10.1119/1.2209246 . Lipscombe, Trevor Davis (2009). Physics of rugby ISBN 1-904761-08-9 . OCLC 646827222 . https://www.worldcat.org/oclc/646827222 Hongo, TetsuyukiЦ─│Sato, HidenoriЦ─│Iwata, YoshioЦ─│Komatsuzaki, ToshihikoЦ─│Hongo, YokoЦ─▄Modeling and Analysis of Impact System Composed of Ball and Plane. Ц─█Ц─▌Transactions of the Japan Society of Mechanical Engineers Series CЦ─▐Г╛╛65Е╥╩Г╛╛634Е▐╥Ц─│1999Е╧╢Ц─│2287Б─⌠2293И═│Ц─│doi :10.1299/kikaic.65.2287 Ц─│ISSN 1884-8354 Ц─┌ Ф°╗Ф²▒, И╬█Ф╡╩Ц─▄Ф╞■И┤█Ц│╝Е╝÷И╗⌠ Ц─█Ц─▌Е╓╘Ф╟≈Ц─▐Г╛╛59Е╥╩Г╛╛7Е▐╥Ц─│Ф≈╔Ф°╛Ф╟≈Х╠║Е╜╕Д╪ Ц─│2012Е╧╢Ц─│657-660И═│Ц─│ISSN 05460921 Ц─│NAID 110009489349 Ц─│NDLJP :10609325 Ц─┌ Briggs, L. J. (1945). Б─°Methods for measuring the coefficient of restitution and the spin of a ballБ─². Journal of Research of the National Bureau of Standards 34 (1): 1Б─⌠23. doi :10.6028/jres.034.001 . Cross, R. (2011). Physics of Baseball & Softball . Springer . ISBN 978-1-4419-8112-7 Cross (2014Е╧╢6Ф°┬). Б─°Physics of bounce Б─². Sydney University . 2021Е╧╢3Ф°┬22Ф≈╔И√╡Х╕╖Ц─┌ Cross, R. (2015). Б─°Behaviour of a bouncing ballБ─². Physics Education 50 (3): 335Б─⌠341. Bibcode : 2015PhyEd..50..335C . doi :10.1088/0031-9120/50/3/335 . Stronge, W. J. (2004). Impact mechanics . Cambridge University Press . ISBN 978-0-521-60289-1 Erlichson, Herman (1983). Б─°Maximum projectile range with drag and lift, with particular application to golfБ─². American Journal of Physics 51 (4): 357Б─⌠362. Bibcode : 1983AmJPh..51..357E . doi :10.1119/1.13248 . Д╩╡И┤▌, Г╢■Г╚═Ц─▄Е╧ЁИ²╒Д╦┼Ц│╖Ц│╝И²·Е╪╬Ф─╖Х║²Г╙│ Б─∙ Ц│²Ц│╝Г░├Х╚√Ц│╗Е╝÷И ⌡ Б─∙ Ц─█О╪┬PDFО╪┴Ц─▌Г÷╔Х┐╫Ц│╗Ф┼─Х║⌠Ц─▐Г╛╛53Е╥╩Ц─│2018Е╧╢Ц─│22-27И═│Ц─│2021Е╧╢11Ф°┬2Ф≈╔И√╡Х╕╖ Ц─┌ Д╦┼ЕЁ╤, Ф┘╤Ц─│Г┴⌡Е╠╠, Е╧╦Е╫╕Ц─│Е┘╚Е²┌, Е┴⌡Е▐╡Ц─│Е╓╖Е╨╜, Ф≤▄Ф≤╜Ц─▄Е█⌠Г░┐Ц┐°Ц┐╪Ц┐╚Ц│╝Иё⌡Х║▄Д╦╜Ц│╚Ц│┼Ц│▒Ц┌▀Е⌡·Х╩╒Ф∙╟Ц│╝Е╓┴Е▄√Ц│╚Ц│╓Ц│└Ц│╕ Ц─█Ц─▌Ф√╟Ф╫÷Д╫⌠Х┌╡Е╜╕Г═■Г╘╤Ц─▐Г╛╛32Е╥╩Ц─│Ф√╟Ф╫÷Г°▄Д╫⌠Х┌╡Е╜╕Д╪ Ц─│2014Е╧╢3Ф°┬Ц─│3-10И═│Ц─│ISSN 2186-7119 Ц─│NAID 120006808018 Ц─┌