õĮÖńŁēÕī¢ÕŁÉÕ£ÅĶ½¢Ńü½ŃüŖŃüæŃéŗõĮÖńŁēÕī¢ÕŁÉ’╝łŃéłŃü©ŃüåŃüŗŃüŚŃĆüĶŗ▒: coequalizer , coequaliser’╝ēŃü»ÕÉīÕĆżķ¢óõ┐éŃü½ŃéłŃéŗÕĢåŃü«ŃĆüõ╗╗µäÅŃü«Õ£ÅŃü½ŃüŖŃüæŃéŗÕ»ŠĶ▒ĪŃü½Õ»ŠŃüÖŃéŗõĖĆĶł¼Õī¢Ńü¦ŃüéŃéŗŃĆéõĮÖńŁēÕī¢ÕŁÉŃü»ńŁēÕī¢ÕŁÉŃü«ÕÅīÕ»ŠŃü©Ńü¬ŃéŗÕ£ÅĶ½¢ńÜ䵦ŗµłÉŃü¦ŃüéŃéŗŃĆé Õ«ÜńŠ®õĮÖńŁēÕī¢ÕŁÉŃü»õ║īŃüżŃü«Õ»ŠĶ▒Ī X, Y Ńü©õ║īŃüżŃü«Õ╣│ĶĪīÕ░ä f, g: X ŌåÆ Y ŃüŗŃéēŃü¬ŃéŗÕø│Õ╝ÅŃü«õĮÖµźĄķÖÉŃü¦ŃüéŃéŗŃĆéŃéłŃéŖµśÄńż║ńÜäŃü½µøĖŃüæŃü░ŃĆüõĮÖńŁēÕī¢ÕŁÉŃü»Õ»ŠĶ▒Ī Q Ńü©Õ░ä q: Y ŌåÆ Q Ńü¦ q Ōłś f = q Ōłś g ŃéƵ║ĆŃü¤ŃüÖŃééŃü«Ńü«ńĄäŃü©ŃüŚŃü”Õ«ÜńŠ®ŃüÖŃéŗŃüōŃü©ŃüīŃü¦ŃüŹŃéŗŃĆéŃüĢŃéēŃü½Ķ©ĆŃüłŃü░ŃĆüÕ»Š (Q, q) Ńü»ŃĆüÕÉīŃüśµĆ¦Ķ│¬ŃéƵīüŃüżÕłźŃü«Õ»Š (Q', q') ŃüīõĖÄŃüłŃéēŃéīŃü¤Ńü©ŃüŹŃĆüõ╗źõĖŗŃü«Õø│Õ╝Å 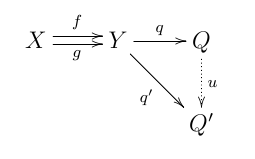 ŃéÆÕÅ»µÅøŃü©ŃüÖŃéŗÕ░ä u: Q ŌåÆ Q' ŃüīõĖƵäÅŃü½ÕŁśÕ£©ŃüÖŃéŗŃü©ŃüäŃüåµäÅÕæ│Ńü¦Ńü«µÖ«ķüŹµĆ¦ŃéƵīüŃü¤Ńü¬ŃüæŃéīŃü░Ńü¬ŃéēŃü¬ŃüäŃĆéÕģ©Ńü”Ńü«µÖ«ķüŹµ¦ŗµłÉŃüīŃüØŃüåŃü¦ŃüéŃéŗķĆÜŃéŖŃĆüõĮÖńŁēÕī¢ÕŁÉŃü»ÕŁśÕ£©ŃüÖŃéīŃü░ÕÉīÕ×ŗŃéÆķÖżŃüäŃü”õĖƵäÅŃü¦ŃüéŃéŗ’╝łŃüØŃéīŃüīŃéåŃüłŃü½ŃĆüõĖÄŃüłŃéēŃéīŃü¤Õ╣│ĶĪīÕ░äŃü«ÕŹśŃü½ (the) õĮÖńŁēÕī¢ÕŁÉŃü©Õæ╝ŃüČŃüōŃü©Ńü½µĘĘõ╣▒Ńü«ĶÖ×Ńü»ńäĪŃüä’╝ēŃĆé õĮÖńŁēÕī¢ÕŁÉ q Ńüīõ╗╗µäÅŃü«Õ£ÅŃü½ŃüŖŃüäŃü”Õģ©Õ×ŗÕ░äŃü¦ŃüéŃéŗŃüōŃü©ŃéÆńż║ŃüÖŃüōŃü©ŃüīŃü¦ŃüŹŃéŗŃĆé õŠŗ
µĆ¦Ķ│¬
ńē╣ÕłźŃü«ÕĀ┤ÕÉłķøČÕ░äŃéƵīüŃüżÕ£ÅŃü½ŃüŖŃüäŃü”Õ░ä f Ńü«õĮÖµĀĖŃüī f Ńü©Õ╣│ĶĪīŃü¬ķøČÕ░äŃü©Ńü«õĮÖńŁēÕī¢ÕŁÉŃü©ŃüŚŃü”Õ«ÜńŠ®Ńü¦ŃüŹŃéŗŃĆé ÕēŹÕŖĀµ│ĢÕ£ÅŃü½ŃüŖŃüäŃü”Õ░äŃü«ÕÆīŃü©ÕĘ«ŃüīµäÅÕæ│ŃéƵīüŃüż’╝łÕ░äķøåÕÉłŃüīÕ«¤ķÜøŃü½ŃéóŃā╝ŃāÖŃā½ńŠżŃéƵłÉŃüÖ’╝ēŃĆéŃüØŃü«ŃéłŃüåŃü¬Õ£ÅŃü½ŃüŖŃüäŃü”ŃĆüõ║īŃüżŃü«Õ░ä f, g Ńü«õĮÖńŁēÕī¢ÕŁÉŃü»ŃüØŃéīŃéēŃü«ÕĘ«Ńü«õĮÖµĀĖŃü©ŃüŚŃü”
Ńü¦Õ«ÜńŠ®Ńü¦ŃüŹŃéŗŃĆé ŃéłŃéŖÕ╝ĘŃüäµ”éÕ┐ĄŃü©ŃüŚŃü”ńĄČÕ»ŠõĮÖńŁēÕī¢ÕŁÉ (absolute coequalizer) ŃüīŃüéŃéŗŃĆéŃüōŃéīŃü»õ╗╗µäÅŃü«ÕćĮµēŗŃü«õĖŗŃü¦õĖŹÕżēŃü¬õĮÖńŁēÕī¢ÕŁÉŃéÆĶ©ĆŃüåŃĆéÕÄ│Õ»åŃü½Ķ©ĆŃüłŃü░ŃĆüգŠØÆ× Ńü½ŃüŖŃüæŃéŗÕ»Š f, g: X ŌåÆ Y Ńü«ńĄČÕ»ŠõĮÖńŁēÕī¢ÕŁÉŃü»ŃĆüõĖŖĶ©śŃü«ķĆÜŃéŖÕ«ÜŃéüŃéēŃéīŃéŗõĮÖńŁēÕī¢ÕŁÉ (Q, q) Ńü¦ŃüéŃüŻŃü”ŃĆüµø┤Ńü¬ŃéŗµĆ¦Ķ│¬Ńü©ŃüŚŃü”õ╗╗µäÅŃü«ÕćĮµēŗ F: ØÆ× ŌåÆ ØƤ Ńü½Õ»ŠŃüŚŃü” (F(Q), F(q)) Ńü»Õ£Å ØƤ Ńü½ŃüŖŃüæŃéŗÕ»Š F(f), F(g) Ńü«õĮÖńŁēÕī¢ÕŁÉŃü©Ńü¬ŃéŗŃü©ŃüäŃüåµØĪõ╗ČŃéƵ║ĆĶČ│ŃüÖŃéŗŃĆéÕłåĶŻéõĮÖńŁēÕī¢ÕŁÉŃü»ńĄČÕ»ŠõĮÖńŁēÕī¢ÕŁÉŃü«õŠŗŃü¦ŃüéŃéŗŃĆé ķ¢óķĆŻķĀģńø«µ│©µäÅ
ÕÅéĶĆāµ¢ćńī«
Õż¢ķā©Ńā¬Ńā│Ńé»
|
Portal di Ensiklopedia Dunia













