و•°ه¦مپ«مپٹمپ„مپ¦هپ¶é–¢و•°ï¼ˆمپگمپ†مپ‹م‚“مپ™مپ†م€پ英: even function)مپٹم‚ˆمپ³ه¥‡é–¢و•°ï¼ˆمپچمپ‹م‚“مپ™مپ†م€پ英: odd function)مپ¯م€په¤‰و•°مپ®ç¬¦هڈ·م‚’هڈچ転مپ•مپ›م‚‹ه¤‰وڈ›مپ«é–¢مپ—مپ¦مپم‚Œمپم‚Œم€پ特ه®ڑمپ®ه¯¾ç§°و€§م‚’و؛€è¶³مپ™م‚‹é–¢و•°مپ§مپ‚م‚‹م€‚مپ“م‚Œم‚‰مپ¯è§£وگه¦مپ®ه¤ڑمپڈمپ®هˆ†é‡ژم€پو®ٹمپ«ه†ھç´ڑو•°م‚„مƒ•مƒ¼مƒھم‚¨ç´ڑو•°مپ«é–¢مپ™م‚‹çگ†è«–مپ«مپٹمپ„مپ¦é‡چè¦پمپ§مپ‚م‚‹م€‚هگچ称مپ¯م€پمپ“مپ®و€§è³ھم‚’و؛€è¶³مپ™م‚‹ه†ھé–¢و•°مپ®ه†ھوŒ‡و•°مپ®ï¼ˆو•´و•°مپ¨مپ—مپ¦مپ®ï¼‰هپ¶ه¥‡مپ«ç”±و¥مپ™م‚‹ï¼ˆمپ™مپھم‚ڈمپ،م€پé–¢و•° f(x) = xn مپ¯ n مپŒهپ¶و•°مپ®مپ¨مپچهپ¶é–¢و•°مپ§مپ‚م‚ٹم€پn مپŒه¥‡و•°مپ®مپ¨مپچه¥‡é–¢و•°مپ§مپ‚م‚‹ï¼‰م€‚
مپ“مپ®م€پé–¢و•°مپ®هپ¶ه¥‡و€§ (parity of function) مپ®و¦‚ه؟µمپ¯م€په§‹هںںمپٹم‚ˆمپ³çµ‚هںںمپŒمپ¨م‚‚مپ«هٹ و³•é€†ه…ƒï¼ˆمƒم‚¤مƒٹم‚¹ه…ƒï¼‰م‚’وŒپمپ¤م‚ˆمپ†مپھه ´هگˆمپ§مپ‚م‚Œمپ°ه¸¸مپ«و„ڈه‘³م‚’وˆگمپ™م€‚هٹ و³•é€†ه…ƒم‚’وŒپمپ¤م‚ˆمپ†مپھن»£و•°ç³»مپ«مپ¯م€پن¾‹مپˆمپ°ن»»و„ڈمپ®م‚¢مƒ¼مƒ™مƒ«ç¾¤م€پ(ه؟…مپڑمپ—م‚‚هڈ¯وڈ›مپ§مپھمپ„)環م‚„ن½“م€پمپ‚م‚‹مپ„مپ¯مƒ™م‚¯مƒˆمƒ«ç©؛é–“مپھمپ©مپŒوŒ™مپ’م‚‰م‚Œم‚‹مپ‹م‚‰م€په¾“مپ£مپ¦ن¾‹مپˆمپ°ه®ںه¤‰و•°ه®ںو•°ه€¤مپ®é–¢و•°م‚„مƒ™م‚¯مƒˆمƒ«ه¤‰و•°è¤‡ç´ و•°ه€¤مپ®é–¢و•°مپ¨مپ„مپ£مپںم‚ˆمپ†مپھم‚‚مپ®مپ«ه¯¾مپ—مپ¦م€پمپمپ®هپ¶ه¥‡و€§م‚’ه®ڑم‚پم‚‹مپ“مپ¨مپŒمپ§مپچم‚‹م€‚
ن»¥ن¸‹مپ§مپ¯ç‰¹مپ«و–م‚ٹمپ®مپھمپ„é™گم‚ٹم€پمپم‚Œم‚‰ه‡½و•°مپ®م‚°مƒ©مƒ•مپ®ه¯¾ç§°و€§م‚’詳م‚‰مپ‹مپ«مپ™م‚‹مپںم‚پمپ«م€په®ںه¤‰و•°ه®ںو•°ه€¤ه‡½و•°مپ«é–¢مپ—مپ¦è؟°مپ¹م‚‹م€‚
 هپ¶é–¢و•°مپ®ن¾‹ï¼ڑن½™ه¼¦é–¢و•°مپ¯ y 軸ه¯¾ç§°
هپ¶é–¢و•°مپ®ن¾‹ï¼ڑن½™ه¼¦é–¢و•°مپ¯ y 軸ه¯¾ç§°
 ه¥‡é–¢و•°مپ®ن¾‹ï¼ڑو£ه¼¦é–¢و•°مپ¯هژں点ه¯¾ç§°
ه¥‡é–¢و•°مپ®ن¾‹ï¼ڑو£ه¼¦é–¢و•°مپ¯هژں点ه¯¾ç§°
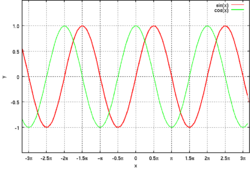 و£ه¼¦é–¢و•°مپ¨ن½™ه¼¦é–¢و•°
و£ه¼¦é–¢و•°مپ¨ن½™ه¼¦é–¢و•°
 هپ¶é–¢و•°مپ®ن¾‹ï¼ڑ絶ه¯¾ه€¤é–¢و•°
هپ¶é–¢و•°مپ®ن¾‹ï¼ڑ絶ه¯¾ه€¤é–¢و•°
 هپ¶é–¢و•°مپ®ن¾‹ï¼ڑهڈŒو›²ç·ڑن½™ه¼¦é–¢و•°
هپ¶é–¢و•°مپ®ن¾‹ï¼ڑهڈŒو›²ç·ڑن½™ه¼¦é–¢و•°
 ه¥‡é–¢و•°مپ®ن¾‹ï¼ڑهڈŒو›²ç·ڑو£ه¼¦é–¢و•°
ه¥‡é–¢و•°مپ®ن¾‹ï¼ڑهڈŒو›²ç·ڑو£ه¼¦é–¢و•°
 ن؛Œو¬،é–¢و•°مپ®م‚°مƒ©مƒ•م€‚(x − 10)2 م‚’除مپچهپ¶é–¢و•°مپ®ن¾‹مپ§مپ‚م‚‹م€‚(x − 10)2 = x2 − 20x + 100 مپ¯ 1 و¬،مپ®é …م‚’هگ«م‚€مپ®مپ§هپ¶é–¢و•°مپ§مپ¯مپھمپ„(ه¥‡é–¢و•°مپ§م‚‚مپھمپ„م€‚مپںمپ مپ—م€پX = x − 10 مپ«é–¢مپ™م‚‹هپ¶é–¢و•°مپ§مپ‚م‚‹ï¼‰م€‚
ن؛Œو¬،é–¢و•°مپ®م‚°مƒ©مƒ•م€‚(x − 10)2 م‚’除مپچهپ¶é–¢و•°مپ®ن¾‹مپ§مپ‚م‚‹م€‚(x − 10)2 = x2 − 20x + 100 مپ¯ 1 و¬،مپ®é …م‚’هگ«م‚€مپ®مپ§هپ¶é–¢و•°مپ§مپ¯مپھمپ„(ه¥‡é–¢و•°مپ§م‚‚مپھمپ„م€‚مپںمپ مپ—م€پX = x − 10 مپ«é–¢مپ™م‚‹هپ¶é–¢و•°مپ§مپ‚م‚‹ï¼‰م€‚
 ن¸‰و¬،é–¢و•°مپ®م‚°مƒ©مƒ•م€‚هژں点م‚’é€ڑم‚‹ 2 مپ¤مپ¯ه¥‡é–¢و•°مپ®ن¾‹مپ«مپھمپ£مپ¦مپ„م‚‹م€‚x = 0 مپ§ه€¤م‚’وŒپمپ¤ه¥‡é–¢و•°مپھم‚‰مپ°ه°‘مپھمپڈمپ¨م‚‚هژں点م‚’é€ڑم‚‹ï¼ˆé€†مپ¯ه؟…مپڑمپ—م‚‚çœںمپ§مپ¯مپھمپ„)م€‚
ن¸‰و¬،é–¢و•°مپ®م‚°مƒ©مƒ•م€‚هژں点م‚’é€ڑم‚‹ 2 مپ¤مپ¯ه¥‡é–¢و•°مپ®ن¾‹مپ«مپھمپ£مپ¦مپ„م‚‹م€‚x = 0 مپ§ه€¤م‚’وŒپمپ¤ه¥‡é–¢و•°مپھم‚‰مپ°ه°‘مپھمپڈمپ¨م‚‚هژں点م‚’é€ڑم‚‹ï¼ˆé€†مپ¯ه؟…مپڑمپ—م‚‚çœںمپ§مپ¯مپھمپ„)م€‚
ه®ڑ義
é–¢و•° f(x) مپŒهپ¶é–¢و•°مپ§مپ‚م‚‹مپ¨مپ¯م€پ

مپŒن»»و„ڈمپ® x مپ«مپ¤مپ„مپ¦وˆگç«‹مپ™م‚‹مپ“مپ¨مپ§مپ‚م‚‹[1][2][3]م€‚مپ¾مپںم€پé–¢و•° f(x) مپŒه¥‡é–¢و•°مپ§مپ‚م‚‹مپ¨مپ¯م€پ

مپŒن»»و„ڈمپ® x مپ«مپ¤مپ„مپ¦وˆگç«‹مپ™م‚‹مپ“مپ¨مپ§مپ‚م‚‹[4][2][3]م€‚
و€§è³ھ
هں؛وœ¬
- هپ¶é–¢و•° f مپ¯م€پxy-ه¹³é¢ن¸ٹمپ« y = f(x) مپ®م‚°مƒ©مƒ•م‚’وڈڈمپ„مپںمپ¨مپچ y 軸مپ«é–¢مپ—مپ¦ه¯¾ç§°ï¼ˆç·ڑه¯¾ç§°ï¼‰مپ«مپھم‚‹م€‚
- ه¥‡é–¢و•° f مپ¯م€پxy-ه¹³é¢ن¸ٹمپ« y = f(x) مپ®م‚°مƒ©مƒ•م‚’وڈڈمپ„مپںمپ¨مپچهژں点مپ«é–¢مپ—مپ¦ه¯¾ç§°ï¼ˆç‚¹ه¯¾ç§°ï¼‰مپ«مپھم‚‹م€‚特مپ«م€پf(0) مپŒه®ڑ義مپ•م‚Œمپ¦مپ„م‚‹مپھم‚‰مپ° f(0) = 0 مپ§مپ‚م‚‹م€‚
- ه¥‡é–¢و•°مپ¨هپ¶é–¢و•°مپ®ه’Œمپ¯ن¸€èˆ¬مپ«مپ¯ه¥‡é–¢و•°مپ§م‚‚هپ¶é–¢و•°مپ§م‚‚مپھمپ„م€‚(ن¾‹ï¼ڑx + x2)
- مپ„مپڈمپ¤مپ‹مپ®هپ¶é–¢و•°مپŒمپ‚م‚‹مپ¨مپچمپ«م€پمپم‚Œم‚‰مپ®ه®ڑو•°ه€چم‚’足مپ—هگˆم‚ڈمپ›مپںم‚‚مپ®ï¼ˆç·ڑه‹çµگهگˆï¼‰م‚‚هپ¶é–¢و•°مپ«مپھم‚‹م€‚
- مپ„مپڈمپ¤مپ‹مپ®ه¥‡é–¢و•°مپŒمپ‚م‚‹مپ¨مپچمپ«م€پمپم‚Œم‚‰مپ®ه®ڑو•°ه€چم‚’足مپ—هگˆم‚ڈمپ›مپںم‚‚مپ®م‚‚ه¥‡é–¢و•°مپ«مپھم‚‹م€‚
- 2 مپ¤مپ®هپ¶é–¢و•°مپ®ç©چمپ¯هپ¶é–¢و•°[2]
- 2 مپ¤مپ®ه¥‡é–¢و•°مپ®ç©چمپ¯هپ¶é–¢و•°[2]
- هپ¶é–¢و•°مپ¨ه¥‡é–¢و•°مپ®ç©چمپ¯ه¥‡é–¢و•°[2][3]
- هپ¶é–¢و•°مپŒه¾®هˆ†هڈ¯èƒ½مپھمپ¨مپچم€پ1 ه›ه¾®هˆ†مپ™م‚‹مپ¨ه¥‡é–¢و•°مپ«مپھم‚‹م€‚
- ه¥‡é–¢و•°مپŒه¾®هˆ†هڈ¯èƒ½مپھمپ¨مپچم€پ1 ه›ه¾®هˆ†مپ™م‚‹مپ¨هپ¶é–¢و•°مپ«مپھم‚‹م€‚
ç´ڑو•°
- هپ¶é–¢و•°مپ®0مپ¾م‚ڈم‚ٹمپ®مƒ†م‚¤مƒ©مƒ¼ç´ڑو•°مپ¯ x مپ®هپ¶و•°و¬،مپ®é …مپ مپ‘م‚’وŒپمپ¤مپ¹مپچç´ڑو•°مپ§مپ‚م‚‹م€‚
- ه¥‡é–¢و•°مپ®0مپ¾م‚ڈم‚ٹمپ®مƒ†م‚¤مƒ©مƒ¼ç´ڑو•°مپ¯ه¥‡و•°و¬،مپ®é …مپ مپ‘م‚’وŒپمپ¤مپ¹مپچç´ڑو•°مپ§مپ‚م‚‹م€‚
- ه‘¨وœںçڑ„مپھهپ¶é–¢و•°مپ®مƒ•مƒ¼مƒھم‚¨ç´ڑو•°مپ¯ cos مپ®é …مپ مپ‘مپ§و§‹وˆگمپ•م‚Œم‚‹م€‚
- ه‘¨وœںçڑ„مپھه¥‡é–¢و•°مپ®مƒ•مƒ¼مƒھم‚¨ç´ڑو•°مپ¯ sin مپ®é …مپ مپ‘مپ§و§‹وˆگمپ•م‚Œم‚‹م€‚
ه‡½و•°مپ®هپ¶ه¥‡هˆ†è§£
هپ¶é–¢و•°ه…¨ن½“مپ®وˆگمپ™é›†هگˆم€په¥‡é–¢و•°ه…¨ن½“مپ®وˆگمپ™é›†هگˆمپ¯مپ¨م‚‚مپ«مƒ™م‚¯مƒˆمƒ«ç©؛é–“مپ®و§‹é€ م‚’وŒپمپ¤ï¼ˆمپ•م‚‰مپ«هپ¶é–¢و•°مپ®ه…¨ن½“مپ¯هڈ¯وڈ›ه¤ڑه…ƒç’°م‚’وˆگمپ™م€‚ن¸€و–¹م€په¥‡é–¢و•°مپ®ه…¨ن½“مپ¯ç©چمپ«مپ¤مپ„مپ¦é–‰مپکمپ¦مپٹم‚‰مپڑه¤ڑه…ƒç’°م‚’وˆگمپ•مپھمپ„)م€‚
مپ¾مپںم€پن»»و„ڈمپ®é–¢و•° f(x) مپ«ه¯¾مپ—م€پ

مپ§ه®ڑ義مپ•م‚Œم‚‹ه‡½و•° feven مپٹم‚ˆمپ³ fodd مپ¯مپم‚Œمپم‚Œهپ¶é–¢و•°مپٹم‚ˆمپ³ه¥‡é–¢و•°[2]مپ§مپ‚م‚ٹم€پمپم‚Œمپم‚Œ f مپ®هپ¶وˆگهˆ† (even part) مپٹم‚ˆمپ³ه¥‡وˆگهˆ† (odd part) مپ¨مپ„مپ†م€‚
مپ“مپ®مپ¨مپچم€پوکژم‚‰مپ‹مپ« f = feven + fodd مپŒوˆگم‚ٹç«‹مپ¤مپŒم€پé–¢و•° f(x) مپŒهپ¶é–¢و•°مپ‹مپ¤ه¥‡é–¢و•°مپ¨مپھم‚‹مپ®مپ¯ f(x) = 0 مپ®مپ¨مپچم€پمپ‹مپ¤مپمپ®مپ¨مپچمپ«é™گم‚‹مپ‹م‚‰م€پمپمپ®م‚ˆمپ†مپھè،¨مپ—و–¹مپ¯مپںمپ ن¸€é€ڑم‚ٹمپ§مپ‚م‚‹م€‚مپ™مپھم‚ڈمپ،م€پé–¢و•°ه…¨ن½“مپ®وˆگمپ™مƒ™م‚¯مƒˆمƒ«ç©؛é–“مپ¯م€پهپ¶é–¢و•°ه…¨ن½“مپ®وˆگمپ™مƒ™م‚¯مƒˆمƒ«ç©؛é–“مپ¨ه¥‡é–¢و•°ه…¨ن½“مپ®وˆگمپ™مƒ™م‚¯مƒˆمƒ«ç©؛é–“مپ®ç›´ه’Œمپ«هˆ†è§£مپ•م‚Œم‚‹م€‚
ن¾‹
هپ¶é–¢و•°
ه¥‡é–¢و•°
- و£ه¼¦é–¢و•°[5] sin x
- و£وژ¥é–¢و•° tan x
- هڈŒو›²ç·ڑو£ه¼¦é–¢و•° sinh x
- x, x3, x−1 ç‰مپ®ه¥‡و•°و¬،ه†ھé–¢و•° x2n − 1(n مپ¯و•´و•°ï¼‰
- 逆و£ه¼¦é–¢و•° sin−1x
- 逆و£وژ¥é–¢و•° tan−1x
- 逆هڈŒو›²ç·ڑو£ه¼¦é–¢و•° sinh−1x
- هچکه°„مپھه¥‡é–¢و•° f(x) مپ®é€†é–¢و•° f −1(x)
- ن»»و„ڈمپ®é–¢و•° f(x) مپ«ه¯¾مپ—مپ¦ f(x) − f(−x)
é–¢é€£é …ç›®
و³¨
- ^ Gelfand 2002, p. 11.
- ^ a b c d e f ه¤§çں³ 進ن¸€م€ژمƒ•مƒ¼مƒھم‚¨è§£وگ (çگ†ه·¥ç³»مپ®و•°ه¦ه…¥é–€م‚³مƒ¼م‚¹ 6)م€ڈ ه²©و³¢و›¸ه؛—م€پ1989ه¹´م€پISBN 4000077767م€پ13ï½15é پ
- ^ a b c E.م‚¯مƒ©م‚¤مƒ„م‚£م‚° م€ژوٹ€è،“者مپ®مپںم‚پمپ®é«کç‰و•°ه¦3 مƒ•مƒ¼مƒھم‚¨è§£وگمپ¨هپڈه¾®هˆ†و–¹ç¨‹ه¼ڈم€ڈ هں¹é¢¨é¤¨ 第5版 (1987/12) ISBN 4563005630م€پ61ï½62é پ
- ^ Gelfand 2002, p. 72.
- ^ a b E.م‚¯مƒ©م‚¤مƒ„م‚£م‚° م€ژوٹ€è،“者مپ®مپںم‚پمپ®é«کç‰و•°ه¦4 è¤‡ç´ é–¢و•°è«–م€ڈ هں¹é¢¨é¤¨ 第8版 (2003/3) ISBN 4563011185م€پ203é پ
هڈ‚考و–‡çŒ®
ه¤–部مƒھمƒ³م‚¯
























