гҒ“гҒ®й …зӣ®гҖҢ
еҸҚеҜҫз§°дәӨжҸӣзӣёдә’дҪңз”Ё гҖҚгҒҜзҝ»иЁігҒ•гӮҢгҒҹгҒ°гҒӢгӮҠгҒ®гӮӮгҒ®гҒ§гҒҷгҖӮдёҚиҮӘ然гҒӮгӮӢгҒ„гҒҜжӣ–жҳ§гҒӘиЎЁзҸҫгҒӘгҒ©гҒҢеҗ«гҒҫгӮҢгӮӢеҸҜиғҪжҖ§гҒҢгҒӮгӮҠгҖҒгҒ“гҒ®гҒҫгҒҫгҒ§гҒҜиӘӯгҒҝгҒҘгӮүгҒ„гҒӢгӮӮгҒ—гӮҢгҒҫгҒӣгӮ“гҖӮпјҲеҺҹж–Үпјҡ
en: Antisymmetric exchange пјү
дҝ®жӯЈгҖҒеҠ зӯҶгҒ«еҚ”еҠӣгҒ—гҖҒзҸҫеңЁгҒ®иЎЁзҸҫгӮ’гӮҲгӮҠиҮӘ然гҒӘиЎЁзҸҫгҒ«гҒ—гҒҰдёӢгҒ•гӮӢж–№гӮ’жұӮгӮҒгҒҰгҒ„гҒҫгҒҷгҖӮ
гғҺгғјгғҲгғҡгғјгӮё гӮ„
еұҘжӯҙ гӮӮеҸӮз…§гҒ—гҒҰгҒҸгҒ гҒ•гҒ„гҖӮ
пјҲ2023е№ҙ10жңҲ пјү
гӮёгғЈгғӯгӮ·гғігӮ№гӮӯгғјгғ»е®Ҳи°·гғҷгӮҜгғҲгғ«гҒ®еҗ‘гҒҚгҒҜеұҖжүҖж§ӢйҖ гҒ«гӮҲгӮҠжұәгҒҫгӮӢ зү©зҗҶеӯҰ гҒ«гҒҠгҒ„гҒҰгҖҒеҸҚеҜҫз§°дәӨжҸӣзӣёдә’дҪңз”Ё пјҲгҒҜгӮ“гҒҹгҒ„гҒ—гӮҮгҒҶгҒ“гҒҶгҒӢгӮ“гҒқгҒҶгҒ”гҒ•гӮҲгҒҶгҖҒиӢұ : Antisymmetric exchange пјүгҖҒгҒҫгҒҹгҒҜгӮёгғЈгғӯгӮ·гғігӮ№гӮӯгғјгғ»е®Ҳи°·зӣёдә’дҪңз”Ё пјҲиӢұ : DzyaloshinskiiвҖ“Moriya interaction, DMI пјүгҒЁгҒҜгҖҒзЈҒж°—дәӨжҸӣзӣёдә’дҪңз”ЁгҒ®гҒҶгҒЎгҖҒ2гҒӨгҒ®йҡЈжҺҘгҒҷгӮӢзЈҒж°—гӮ№гғ”гғі
S
i
{\displaystyle {\boldsymbol {S}}_{i}}
S
j
{\displaystyle {\boldsymbol {S}}_{j}}
H
i
,
j
(
D
M
)
=
D
i
j
вӢ…
(
S
i
Г—
S
j
)
{\displaystyle H_{i,j}^{\rm {(DM)}}={\boldsymbol {D}}_{ij}\cdot ({\boldsymbol {S}}_{i}\times {\boldsymbol {S}}_{j})}
зЈҒ気秩еәҸгҒ®гҒӘгҒ„зі»гҒ«гҒҠгҒ„гҒҰгҒҜгӮ№гғ”гғізЈҒж°—гғўгғјгғЎгғігғҲгҒҜе№іиЎҢгӮӮгҒ—гҒҸгҒҜеҸҚе№іиЎҢж–№еҗ‘гҒ«жҸғгҒҶгҒ“гҒЁгӮ’еҘҪгӮҖгҒҢгҖҒзЈҒ気秩еәҸ гӮ’жҢҒгҒӨзі»гҒ«гҒҠгҒ„гҒҰгҒҜгҖҒгӮ№гғ”гғіеӮҫж–ң пјҲиӢұиӘһзүҲ пјү еҸҚеј·зЈҒжҖ§ дҪ“гҒ«гҒҠгҒ‘гӮӢејұгҒ„еј·зЈҒжҖ§ дҪ“зҡ„гҒөгӮӢгҒҫгҒ„гҒҢз”ҹгҒҳгӮӢгҖӮеҸҚеҜҫз§°дәӨжҸӣзӣёдә’дҪңз”ЁгҒҜзЈҒж°—гӮ№гӮӯгғ«гғҹгӮӘгғі гҒҢз”ҹгҒҳгӮӢеҺҹеӣ гҒ§гҒӮгӮҠгҖҒзЈҒжҖ§еј·иӘҳйӣ»дҪ“ пјҲиӢұиӘһзүҲ пјү
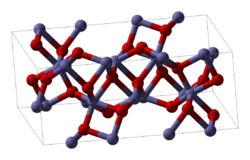
йү„йүұзҹі гҒ®дё»жҲҗеҲҶгҖҒОұ 2 O3 гҒ®гғҳгғһгӮҝгӮӨгғҲ ж§ӢйҖ гҖӮеҸҚеҜҫз§°дәӨжҸӣзӣёдә’дҪңз”ЁгҒ®зҷәиҰӢгҒ®з«Ҝз·’гҒЁгҒ—гҒҰгҖҒ20дё–зҙҖ еҲқй ӯгҒ«е…ёеһӢзҡ„гҒ«гҒҜеҸҚеј·зЈҒжҖ§гӮ’зӨәгҒҷОұ 2 O3 зөҗжҷ¶гҒҢејұгҒ„еј·зЈҒжҖ§гӮ’зӨәгҒҷгҒ“гҒЁгҒҢиҰіжё¬гҒ•гӮҢгҒҹ[ 1] 1958е№ҙ гҖҒгӮӨгғјгӮҙгғӘгғ»гӮёгғЈгғӯгӮ·гғігӮ№гӮӯгғј гҒҜгғ©гғігғҖгӮҰ гҒ®2ж¬Ўзӣёи»ўз§»зҗҶи«– пјҲиӢұиӘһзүҲ пјү [ 2] 1960е№ҙ гҖҒе®Ҳи°·дәЁ гҒҜгӮ№гғ”гғіи»ҢйҒ“зӣёдә’дҪңз”Ё гҒҢеҸҚеҜҫз§°дәӨжҸӣзӣёдә’дҪңз”ЁгҒ®еҫ®иҰ–зҡ„гҒӘж©ҹж§ӢгҒ§гҒӮгӮӢгҒ“гҒЁгӮ’гҒӨгҒҚгҒЁгӮҒ[ 1] и¶…дәӨжҸӣзӣёдә’дҪңз”Ё гҒ®еҸҚеҜҫз§°йғЁеҲҶгҖҚгҒЁе‘јгӮ“гҒ гҖӮ1962е№ҙ гҒ«гғҷгғ«з ”究жүҖ гҒ®D. TrevesгҒЁS. AlexanderгҒҢгҒ“гҒ®з”ЁиӘһгӮ’еҚҳзҙ”еҢ–гҒ—гҒҰеҸҚеҜҫз§°зӣёдә’дҪңз”ЁгҒЁе‘јгӮ“гҒ гҖӮгӮёгғЈгғӯгӮ·гғігӮ№гӮӯгғјгҒЁе®Ҳи°·гҒ®иІўзҢ®гӮ’гҒҹгҒҹгҒҲгҒҰгӮёгғЈгғӯгӮ·гғігӮ№гӮӯгғјгғ»е®Ҳи°·зӣёдә’дҪңз”Ё гҒЁгӮӮе‘јгҒ°гӮҢгӮӢ[ 3]
DMIгҒ®й–ўж•°еҪўгҒҜгӮўгғігғҖгғјгӮҪгғі гҒ«гӮҲгӮӢи¶…дәӨжҸӣзӣёдә’дҪңз”Ё иЎЁејҸгҒ§жӣёгҒӢгӮҢгҒҹгӮӨгӮӘгғі
i
,
j
{\displaystyle i,j}
гӮ№гғ”гғіи»ҢйҒ“зӣёдә’дҪңз”Ё
L
^
вӢ…
S
^
{\displaystyle {\hat {\boldsymbol {L}}}\cdot {\hat {\boldsymbol {S}}}}
ж‘ӮеӢ• и§ЈжһҗгҒҷгӮӢгҒ“гҒЁгҒ«гӮҲгӮҠеҫ—гӮүгӮҢгӮӢ[ 1]
L
^
i
{\displaystyle {\hat {\boldsymbol {L}}}_{i}}
i и§’йҒӢеӢ•йҮҸжј”з®—еӯҗ гҖҒ
S
^
i
{\displaystyle {\hat {\boldsymbol {S}}}_{i}}
гӮ№гғ”гғіжј”з®—еӯҗ гӮ’гҒӮгӮүгӮҸгҒҷгӮӮгҒ®гҒЁгҒҷгӮӢгҖӮ
Оҙ
E
=
вҲ‘
m
[
вҹЁ
n
|
О»
L
^
i
вӢ…
S
^
i
|
m
вҹ©
2
J
(
m
n
вҖІ
n
n
вҖІ
)
S
^
i
вӢ…
S
^
j
E
n
вҲ’
E
m
+
2
J
(
n
n
вҖІ
m
n
вҖІ
)
S
^
i
вӢ…
S
^
j
вҹЁ
m
|
О»
L
^
i
вӢ…
S
^
i
|
n
вҹ©
E
n
вҲ’
E
m
]
+
вҲ‘
m
вҖІ
[
вҹЁ
m
вҖІ
|
О»
L
^
j
вӢ…
S
^
j
|
m
вҹ©
2
J
(
m
вҖІ
n
n
вҖІ
n
)
S
^
i
вӢ…
S
^
j
E
n
вҖІ
вҲ’
E
m
вҖІ
+
2
J
(
n
вҖІ
n
m
вҖІ
n
)
S
^
i
вӢ…
S
^
j
вҹЁ
m
вҖІ
|
О»
L
^
j
вӢ…
S
^
j
|
n
вҖІ
вҹ©
E
n
вҖІ
вҲ’
E
m
вҖІ
]
{\displaystyle {\begin{aligned}\delta E=\sum _{m}&{\Biggl [}{\frac {\langle n|\lambda {\hat {\boldsymbol {L}}}_{i}\cdot {\hat {\boldsymbol {S}}}_{i}|m\rangle 2J(mn'nn'){\hat {\boldsymbol {S}}}_{i}\cdot {\hat {\boldsymbol {S}}}_{j}}{E_{n}-E_{m}}}\\&+{\frac {2J(nn'mn'){\hat {\boldsymbol {S}}}_{i}\cdot {\hat {\boldsymbol {S}}}_{j}\langle m|\lambda {\hat {\boldsymbol {L}}}_{i}\cdot {\hat {\boldsymbol {S}}}_{i}|n\rangle }{E_{n}-E_{m}}}{\Biggr ]}\\+\sum _{m'}&{\Biggl [}{\frac {\langle m'|\lambda {\hat {\boldsymbol {L}}}_{j}\cdot {\hat {\boldsymbol {S}}}_{j}|m\rangle 2J(m'nn'n){\hat {\boldsymbol {S}}}_{i}\cdot {\hat {\boldsymbol {S}}}_{j}}{E_{n'}-E_{m'}}}\\&+{\frac {2J(n'nm'n){\hat {\boldsymbol {S}}}_{i}\cdot {\hat {\boldsymbol {S}}}_{j}\langle m'|\lambda {\hat {\boldsymbol {L}}}_{j}\cdot {\hat {\boldsymbol {S}}}_{j}|n'\rangle }{E_{n'}-E_{m'}}}{\Biggr ]}\end{aligned}}}
гҒ“гҒ“гҒ§гҖҒ
J
{\displaystyle J}
J
(
n
n
вҖІ
m
m
вҖІ
)
=
вҲ«
вҲ«
П•
n
вҲ—
(
r
1
вҲ’
R
)
П•
n
вҖІ
вҲ—
(
r
2
вҲ’
R
вҖІ
)
e
2
r
12
П•
m
(
r
2
вҲ’
R
)
П•
m
вҖІ
(
r
1
вҲ’
R
вҖІ
)
d
r
1
d
r
2
{\displaystyle J(nn'mm')=\int \int \phi _{n}^{*}({\boldsymbol {r_{1}}}-{\boldsymbol {R}})\phi _{n'}^{*}({\boldsymbol {r_{2}}}-{\boldsymbol {R'}}){\frac {e^{2}}{r_{12}}}\phi _{m}({\boldsymbol {r_{2}}}-{\boldsymbol {R}})\phi _{m'}({\boldsymbol {r_{1}}}-{\boldsymbol {R'}})\mathrm {d} {\boldsymbol {r_{1}}}\mathrm {d} {\boldsymbol {r_{2}}}}
гҒҫгҒҹгҖҒ
П•
n
(
r
вҲ’
R
)
{\displaystyle \phi _{n}({\boldsymbol {r}}-{\boldsymbol {R}})}
R
{\displaystyle {\boldsymbol {R}}}
L
{\displaystyle {\boldsymbol {L}}}
Оҙ
E
{\displaystyle \delta E}
Оҙ
E
=
2
О»
вҲ‘
m
J
(
n
n
вҖІ
m
n
вҖІ
)
E
n
вҲ’
E
m
вҹЁ
n
|
L
i
|
m
вҹ©
вӢ…
[
S
i
,
(
S
i
вӢ…
S
j
)
]
+
2
О»
вҲ‘
m
вҖІ
J
(
n
n
вҖІ
n
m
вҖІ
)
E
n
вҖІ
вҲ’
E
m
вҖІ
вҹЁ
n
вҖІ
|
L
j
|
m
вҖІ
вҹ©
вӢ…
[
S
j
,
(
S
i
вӢ…
S
j
)
]
=
2
i
О»
вҲ‘
m
,
m
вҖІ
[
J
(
n
n
вҖІ
m
n
вҖІ
)
E
n
вҲ’
E
m
вҹЁ
n
|
L
i
|
m
вҹ©
вҲ’
J
(
n
n
вҖІ
n
m
вҖІ
)
E
n
вҖІ
вҲ’
E
m
вҖІ
вҹЁ
n
вҖІ
|
L
j
|
m
вҖІ
вҹ©
]
вӢ…
[
S
i
Г—
S
j
]
=
D
i
j
вӢ…
[
S
i
Г—
S
j
]
.
{\displaystyle {\begin{aligned}\delta E&=2\lambda \sum \limits _{m}{\frac {J(nn'mn')}{E_{n}-E_{m}}}\langle n|{\boldsymbol {L_{i}}}|m\rangle \cdot [{\boldsymbol {S_{i}}},({\boldsymbol {S_{i}}}\cdot {\boldsymbol {S_{j}}})]\\&+2\lambda \sum _{m'}{\frac {J(nn'nm')}{E_{n'}-E_{m'}}}\langle n'|{\boldsymbol {L_{j}}}|m'\rangle \cdot [{\boldsymbol {S_{j}}},({\boldsymbol {S_{i}}}\cdot {\boldsymbol {S_{j}}})]\\&=2i\lambda \sum \limits _{m,m'}\left[{\frac {J(nn'mn')}{E_{n}-E_{m}}}\langle n|{\boldsymbol {L_{i}}}|m\rangle -{\frac {J(nn'nm')}{E_{n'}-E_{m'}}}\langle n'|{\boldsymbol {L_{j}}}|m'\rangle \right]\cdot [{\boldsymbol {S_{i}}}\times {\boldsymbol {S_{j}}}]\\&={\boldsymbol {D}}_{ij}\cdot [{\boldsymbol {S}}_{i}\times {\boldsymbol {S}}_{j}].\end{aligned}}}
е®ҹйҡӣгҒ®зөҗжҷ¶ гҒ§гҒҜгҖҒйҡЈжҺҘгҒҷгӮӢгӮӨгӮӘгғігҒ®еҜҫз§°жҖ§гҒӢгӮүгғҷгӮҜгғҲгғ«
D
i
j
{\displaystyle {\boldsymbol {D}}_{ij}}
A
{\displaystyle A}
B
{\displaystyle B}
A
B
{\displaystyle AB}
дёӯзӮ№
C
{\displaystyle C}
[ 1]
гҒҢеҸҚи»ўеҜҫз§°дёӯеҝғгҒ®е ҙеҗҲгҖҒ
D
=
0
{\displaystyle {\boldsymbol {D}}=0}
A
B
{\displaystyle AB}
йҸЎжҳ еҜҫз§°йқў
Пғ
{\displaystyle \sigma }
C
{\displaystyle C}
D
вҲҘ
Пғ
{\displaystyle {\boldsymbol {D}}\parallel \sigma }
D
вҠҘ
A
B
{\displaystyle {\boldsymbol {D}}\perp AB}
A
{\displaystyle A}
B
{\displaystyle B}
Пғ
{\displaystyle \sigma }
D
вҠҘ
Пғ
{\displaystyle {\boldsymbol {D}}\perp \sigma }
A
B
{\displaystyle AB}
еӣһи»ўеҜҫз§° и»ё
C
2
{\displaystyle C_{2}}
C
{\displaystyle C}
D
вҠҘ
C
2
{\displaystyle {\boldsymbol {D}}\perp C_{2}}
A
B
{\displaystyle AB}
n
{\displaystyle n}
C
n
{\displaystyle C_{n}}
n
вүҘ
2
{\displaystyle n\geq 2}
D
вҲҘ
A
B
{\displaystyle {\boldsymbol {D}}\parallel AB}
е®Ҳи°·гҒ®еҺҹи«–ж–ҮгҒ§и«–гҒҳгӮүгӮҢгӮӢгҒЁгҒҠгӮҠгҖҒгғҷгӮҜгғҲгғ«
D
i
j
{\displaystyle {\boldsymbol {D}}_{ij}}
и¶…дәӨжҸӣзӣёдә’дҪңз”Ё гҒ«гӮҲгӮҠ第дёүгҒ®гӮӨгӮӘгғіпјҲй…ҚдҪҚеӯҗ пјүгҒёдјқйҒ”гҒ•гӮҢгӮӢе ҙеҗҲпјҲеӣігӮ’еҸӮз…§пјүгҖҒ
D
i
j
{\displaystyle {\boldsymbol {D}}_{ij}}
D
i
j
вҲқ
r
i
Г—
r
j
=
r
i
j
Г—
x
{\displaystyle {\boldsymbol {D}}_{ij}\propto {\boldsymbol {r}}_{i}\times {\boldsymbol {r}}_{j}={\boldsymbol {r}}_{ij}\times {\boldsymbol {x}}}
[ 4] [ 5]
D
i
j
{\displaystyle {\boldsymbol {D}}_{ij}}
D
i
j
=
0
{\displaystyle {\boldsymbol {D}}_{ij}=0}
гӮёгғЈгғӯгӮ·гғігӮ№гӮӯгғјгғ»е®Ҳи°·зӣёдә’дҪңз”ЁгҒҜгҖҒгғҗгғ«гӮҜ жқҗж–ҷгҒ«гҒҠгҒ„гҒҰгҒҜгҒқгҒ®еҠ№жһңгҒҢе…ёеһӢзҡ„гҒ«гҒҜејұгҒҸгҖҒд»–гҒ®зЈҒж°—йӣ»ж°—еҠ№жһңгҒЁдјјгҒҰгҒ„гӮӢгҒҹгӮҒе®ҹйЁ“зҡ„гҒ«жё¬е®ҡгҒҷгӮӢгҒ“гҒЁгҒҢеӣ°йӣЈгҒ§гҒӮгӮӢгҖӮгҒ„гҒҫгҒҫгҒ§гҒ«гҖҒXз·ҡеӣһжҠҳе№Іжёү гҖҒгғ–гғӘгғ«гӮўгғіж•Јд№ұ гҖҒйӣ»еӯҗгӮ№гғ”гғіе…ұйіҙ гҖҒдёӯжҖ§еӯҗж•Јд№ұ гӮ’еҲ©з”ЁгҒ—гҒҹDMIгғҷгӮҜгғҲгғ«гӮ’е®ҡйҮҸеҢ–гҒҢи©ҰгҒҝгӮүгӮҢгҒҰгҒҚгҒҰгҒ„гӮӢгҖӮгҒ“гӮҢгӮүгҒ®жҠҖиЎ“гҒ®гҒҶгҒЎеӨҡгҒҸгҒҜзӣёдә’дҪңз”ЁгҒ®еҗ‘гҒҚгҒӢеј·гҒ•гҒӢгҒ®гҒ©гҒЎгӮүгҒӢгҒ—гҒӢжё¬е®ҡгҒ§гҒҚгҒҡгҖҒеҜҫз§°жҖ§гӮӮгҒ—гҒҸгҒҜгӮ№гғ”гғізӣёдә’дҪңз”ЁгӮ«гғғгғ—гғӘгғігӮ°гҒ«гҒӨгҒ„гҒҰйҒҺзЁӢгӮ’зҪ®гҒҸгҖӮиҝ‘е№ҙгҒ®гғ–гғӯгғјгғүгғҗгғігғүйӣ»еӯҗгӮ№гғ”гғіе…ұйіҙгҒЁе…үеӯҰжӨңеҮәгҒЁгҒ®зө„гҒҝеҗҲгӮҸгҒӣ(OD-ESR)гҒ®жҠҖиЎ“зҷәеұ•гҒ«гӮҲгӮҠгҖҒеёҢеңҹйЎһ гӮӨгӮӘгғіжқҗж–ҷгҒ®DMIгғҷгӮҜгғҲгғ«гӮ’гҖҒд»®е®ҡгӮ’зҪ®гҒҸгҒ“гҒЁгҒӘгҒҸгҖҒеәғзҜ„гҒӘзЈҒе ҙеј·еәҰгҒ«гӮҸгҒҹгҒЈгҒҰзү№еҫҙгҒҘгҒ‘гӮӢгҒ“гҒЁгҒҢеҸҜиғҪгҒЁгҒӘгҒЈгҒҹ[ 6]
Оұ 2 O3 гҒҠгӮҲгҒіОұ 2 O3 гҒ®гҒЁгӮӢгӮігғ©гғігғҖгғ еһӢзөҗжҷ¶ж§ӢйҖ пјҲиөӨпјҡйҮ‘еұһгӮӨгӮӘгғігҖҒйқ’пјҡй…ёеҢ–зү©гӮӨгӮӘгғі пјүеҸіеӣігҒ«зӨәгҒҷзөҗжҷ¶ж§ӢйҖ гӮ’жҢҒгҒӨйҮҚйҮ‘еұһй…ёеҢ–зү©гҒҜгҖҒйҮ‘еұһгӮӨгӮӘгғігҒ«гӮҲгҒЈгҒҰеј·зЈҒжҖ§дҪ“гҒ«гӮӮеҸҚеј·зЈҒжҖ§дҪ“гҒ«гӮӮгҒӘгӮӢгҖӮгҒ“гҒ®ж§ӢйҖ гҒҜй…ёеҢ–гӮўгғ«гғҹгғӢгӮҰгғ (AlгӮігғ©гғігғҖгғ еһӢ зөҗжҷ¶ ж§ӢйҖ гҒЁгӮҲгҒ°гӮҢгҖҒR 3 c з©әй–“зҫӨ гҒ«еҲҶйЎһгҒ•гӮҢгӮӢгҖӮгҒ“гҒ®ж§ӢйҖ гҒҜD6 3d з©әй–“зҫӨгӮ’гӮӮгҒӨОұ Оұ еҚҳдҪҚиғһ гӮ’еҗ«гӮҖгҖӮеҸіеӣігҒӢгӮүгҖҒ4гҒӨгҒ®M3+ гӮӨгӮӘгғігҒҢиҸұйқўдҪ“еҚҳдҪҚиғһгҒ®дҪ“еҜҫи§’з·ҡ пјҲиӢұиӘһзүҲ пјү [ жіЁйҮҲ 1] Оұ K Оұ [ 2]
зЈҒж°—гӮ№гӮӯгғ«гғҹгӮӘгғі гҒҜзЈҒеҢ–е ҙгҒ«гҒӮгӮүгӮҸгӮҢгӮӢгғҶгӮҜгӮ№гғҒгғЈгҒ§гҒӮгӮӢгҖӮ жёҰзҠ¶гӮ№гӮӯгғ«гғҹгӮӘгғігҒЁгғҸгғӘгғҚгӮәгғҹзҠ¶гӮ№гӮӯгғ«гғҹгӮӘгғігҒҢгҒӮгӮӢгҒҢгҖҒгҒ©гҒЎгӮүгӮӮгӮёгғЈгғӯгӮ·гғігӮ№гӮӯгғјгғ»е®Ҳи°·зӣёдә’дҪңз”ЁгҒ«гӮҲгӮҠе®үе®ҡеҢ–гҒ•гӮҢгҒҰгҒ„гӮӢгҖӮгӮ№гӮӯгғ«гғҹгӮӘгғігҒҜгҒқгҒ®гғҲгғқгғӯгӮёгӮ«гғ«гҒӘжҖ§иіӘгҒӢгӮүгҖҒж¬Ўдё–д»ЈгҒ®гӮ№гғ”гғігғҲгғӯгғӢгӮҜгӮ№ гғҮгғҗгӮӨгӮ№гҒёгҒ®еҝңз”ЁгҒҢжңҹеҫ…гҒ•гӮҢгҒҰгҒ„гӮӢгҖӮ
еҸҚеҜҫз§°зӣёдә’дҪңз”ЁгҒҜгҖҒиҝ‘е№ҙзҷәиҰӢгҒ•гӮҢгҒҹзЁ®йЎһгҒ®зЈҒжҖ§еј·иӘҳйӣ»дҪ“ пјҲиӢұиӘһзүҲ пјү зЈҒж°—ж§ӢйҖ гҒ«гӮҲгӮҠй…ҚдҪҚгӮӨгӮӘгғігҒ®еҫ®е°ҸеӨүдҪҚгҒҢеј•гҒҚиө·гҒ“гҒ•гӮҢгӮӢгҒ“гҒЁгҒҢгҒӮгӮӢгҖӮгҒ“гӮҢгҒҜгҖҒзЈҒжҖ§еј·иӘҳйӣ»дҪ“гҒҢж јеӯҗгӮЁгғҚгғ«гӮ®гғјгӮ’зҠ зүІгҒ«гҒ—гҒҰгӮӮзЈҒж°—зӣёдә’дҪңз”ЁгӮЁгғҚгғ«гӮ®гғјгӮ’еў—еҠ гҒ•гҒӣгӮӢеӮҫеҗ‘гҒ«гҒӮгӮӢгҒҹгӮҒгҒ§гҒӮгӮӢгҖӮгҒ“гҒ®ж©ҹж§ӢгҒҜгҖҢйҖҶгӮёгғЈгғӯгӮ·гғігӮ№гӮӯгғјгғ»е®Ҳи°·еҠ№жһңгҖҚгҒЁе‘јгҒ°гӮҢгӮӢгҖӮзү№е®ҡгҒ®зЈҒж°—ж§ӢйҖ гҒ®гӮӮгҒЁгҒ§гҒҜгҖҒе…ЁгҒҰгҒ®й…ҚдҪҚгӮӨгӮӘгғігҒҢеҗҢдёҖж–№еҗ‘гҒ«еӨүдҪҚгӮ’еҸ—гҒ‘гҖҒе…ЁдҪ“гҒЁгҒ—гҒҰйӣ»ж°—еҲҶжҘөгҒҢеј•гҒҚиө·гҒ“гҒ•гӮҢгӮӢ[ 5]
гҒ“гҒ®зЈҒж°—йӣ»ж°—зөҗеҗҲгҒ®гҒҹгӮҒгҖҒзЈҒжҖ§еј·иӘҳйӣ»дҪ“гҒҜйӣ»е ҙгҒ®еҚ°еҠ гҒ«гӮҲгӮҠзЈҒж°—гӮ’еҲ¶еҫЎгҒҷгӮӢеҝ…иҰҒгҒ®гҒӮгӮӢеҝңз”ЁдёҠжіЁзӣ®гҒ•гӮҢгҒҰгҒ„гӮӢгҖӮгҒ“гҒ®гӮҲгҒҶгҒӘеҝңз”ЁгҒ®е…·дҪ“дҫӢгҒЁгҒ—гҒҰгҒҜгғҲгғігғҚгғ«зЈҒж°—жҠөжҠ—еҠ№жһң гӮ»гғігӮөгғјгӮ„йӣ»е ҙгҒ«гӮҲгӮӢиӘҝж•ҙж©ҹж§ӢгҒӨгҒҚгҒ®гӮ№гғ”гғігғҗгғ«гғ–гҖҒй«ҳж„ҹеәҰдәӨз•ӘзЈҒе ҙ гӮ»гғігӮөгғјгҖҒйӣ»ж°—зҡ„иӘҝж•ҙж©ҹиғҪгҒӨгҒҚгғһгӮӨгӮҜгғӯжіўгғҮгғҗгӮӨгӮ№гҒӘгҒ©гҒҢжҢҷгҒ’гӮүгӮҢгӮӢ[ 7] [ 8]
гҒ»гҒЁгӮ“гҒ©гҒ®зЈҒжҖ§еј·иӘҳйӣ»дҪ“гҒҜFe3+ гӮӨгӮӘгғігҒЁгғ©гғігӮҝгғӢгғү гӮӨгӮӘгғігӮ’еҗ«гӮҖгҖӮдёӢиЎЁгҒ«гӮҲгҒҸзҹҘгӮүгӮҢгҒҰгҒ„гӮӢзЈҒжҖ§еј·иӘҳйӣ»дҪ“еҢ–еҗҲзү©гҒ®дёҖйғЁгӮ’зӨәгҒҷгҖӮгӮҲгӮҠеӨҡгҒҸгҒ®дҫӢгҒ«гҒӨгҒ„гҒҰгҒҜзЈҒжҖ§еј·иӘҳйӣ»дҪ“ пјҲиӢұиӘһзүҲ пјү
зЈҒжҖ§еј·иӘҳйӣ»дҪ“гҒ®дҫӢ
жқҗж–ҷ
еј·иӘҳйӣ»дҪ“ T C [K]
зЈҒжҖ§дҪ“T N (T C ) [K]
зЁ®еҲҘ
BiFeO пјҲиӢұиӘһзүҲ пјү 1100
653
еӯӨз«Ӣйӣ»еӯҗеҜҫ
HoMn
39[ 9]
зЈҒж°—й§ҶеӢ•
TbMnO
27
42[ 10]
зЈҒж°—й§ҶеӢ•
Ni
6.5[ 11]
MnWO
13.5[ 12]
зЈҒж°—й§ҶеӢ•
CuO
230[ 13]
230
зЈҒж°—й§ҶеӢ•
ZnCr
110[ 14]
20
^ a b c d T. Moriya (1960). вҖңAnisotropic Superexchange Interaction and Weak FerromagnetismвҖқ. Physical Review 120 (1): 91. Bibcode : 1960PhRv..120...91M . doi :10.1103/PhysRev.120.91 .
^ a b I. Dzyaloshinskii (1958). вҖңA thermodynamic theory of "weak" ferromagnetism of antiferromagneticsвҖқ. Journal of Physics and Chemistry of Solids 4 (4): 241. Bibcode : 1958JPCS....4..241D . doi :10.1016/0022-3697(58)90076-3 .
^ D. Treves; S. Alexander (1962). вҖңObservation of antisymmetric exchange interaction in Yttrium OrthoferriteвҖқ. Journal of Applied Physics 33 (3): 1133вҖ“1134. Bibcode : 1962JAP....33.1133T . doi :10.1063/1.1728631 .
^ F. Keffer (1962). вҖңMoriya Interaction and the Problem of the Spin Arrangements in ОІMnSвҖқ. Physical Review 126 (3): 896. Bibcode : 1962PhRv..126..896K . doi :10.1103/PhysRev.126.896 . ^ a b S.-W. Cheong and M. Mostovoy (2007). вҖңMultiferroics: a magnetic twist for ferroelectricityвҖқ . Nature Materials 6 (1): 13вҖ“20. Bibcode : 2007NatMa...6...13C . doi :10.1038/nmat1804 . hdl :11370/f0777dfc-d0d7-4358-8337-c63e7ad007e7 PMID 17199121 . https://www.rug.nl/research/portal/en/publications/multiferroics(f0777dfc-d0d7-4358-8337-c63e7ad007e7).html .
^ Cyril Laplane; Emmanuel Zambrini Cruzeiro; Florian Frowis; Phillipe Goldner; Mikael Afzelius (2016). вҖңHigh-precision measurement of the Dzyaloshinskii-Moriya interaction between two rare-earth ions in a solidвҖқ. Physical Review Letters 117 (3): 037203. arXiv :1605.08444 . Bibcode : 2016PhRvL.117c7203L . doi :10.1103/PhysRevLett.117.037203 . PMID 27472133 .
^ Gajek, M. (2007). вҖңTunnel junctions with multiferroic barriersвҖқ. Nature Materials 6 (4): 296вҖ“302. Bibcode : 2007NatMa...6..296G . doi :10.1038/nmat1860 . PMID 17351615 etal ^ Nan, C. W. (2008). вҖңMultiferroic magnetoelectric composites: Historical perspective, status, and future directionsвҖқ. J. Appl. Phys. 103 (3): 031101вҖ“031101вҖ“35. Bibcode : 2008JAP...103c1101N . doi :10.1063/1.2836410 etal ^ Mihailova, B.; Gospodinov, M. M.; Guttler, G.; Yen, F.; Litvinchuk, A. P.; Iliev, M. N. (2005). вҖңTemperature-dependent Raman spectra of HoMn2 O5 and TbMn2 O5 вҖқ. Phys. Rev. B 71 (17): 172301. Bibcode : 2005PhRvB..71q2301M . doi :10.1103/PhysRevB.71.172301 . ^ Rovillain P. (2010). вҖңMagnetoelectric excitations in multiferroic TbMnO3 by Raman scatteringвҖқ. Phys. Rev. B 81 (5): 054428. arXiv :0908.0061 . Bibcode : 2010PhRvB..81e4428R . doi :10.1103/PhysRevB.81.054428 etal ^ Chaudhury, R. P.; Yen, F.; Dela Cruz, C. R.; Lorenz, B.; Wang, Y. Q.; Sun, Y. Y.; Chu, C. W. (2007). вҖңPressure-temperature phase diagram of multiferroic Ni3 V2 O8 вҖқ . Phys. Rev. B 75 (1): 012407. arXiv :cond-mat/0701576 . Bibcode : 2007PhRvB..75a2407C . doi :10.1103/PhysRevB.75.012407 . http://repository.ust.hk/ir/bitstream/1783.1-18914/1/PhysRevB.75.012407.pdf . ^ Kundys, Bohdan; Simon, Charles; Martin, Christine (2008). вҖңEffect of magnetic field and temperature on the ferroelectric loop in MnWO4 вҖқ. Physical Review B 77 (17): 172402. arXiv :0806.0117 . Bibcode : 2008PhRvB..77q2402K . doi :10.1103/PhysRevB.77.172402 . ^ Jana R. вҖңDirect Observation of Re-entrant Multiferroic CuO at High PressuresвҖқ. arXiv :1508.02874 cond-mat.mtrl-sci ]. ^ Zajdel P. (2017). вҖңStructure and Magnetism in the Bond Frustrated Spinel, ZnCr2 Se4 вҖқ. Phys. Rev. B 95 (13): 134401. arXiv :1701.08227 . Bibcode : 2017PhRvB..95m4401Z . doi :10.1103/PhysRevB.95.134401 etal
^ еӣігҒ§гҒҜиҸұйқўдҪ“жҷ¶гӮ’е…ӯж–№жҷ¶иЎЁзӨәгҒ—гҒҰгҒ„гӮӢгҒҹгӮҒгҖҒиҸұйқўдҪ“еҚҳдҪҚиғһгҒ®дҪ“еҜҫи§’з·ҡгҒҜеӣігҒ®еҚҳдҪҚиғһгҒ®й•·и»ёгҒ«зӣёеҪ“гҒҷгӮӢгҖӮ









![{\displaystyle {\begin{aligned}\delta E=\sum _{m}&{\Biggl [}{\frac {\langle n|\lambda {\hat {\boldsymbol {L}}}_{i}\cdot {\hat {\boldsymbol {S}}}_{i}|m\rangle 2J(mn'nn'){\hat {\boldsymbol {S}}}_{i}\cdot {\hat {\boldsymbol {S}}}_{j}}{E_{n}-E_{m}}}\\&+{\frac {2J(nn'mn'){\hat {\boldsymbol {S}}}_{i}\cdot {\hat {\boldsymbol {S}}}_{j}\langle m|\lambda {\hat {\boldsymbol {L}}}_{i}\cdot {\hat {\boldsymbol {S}}}_{i}|n\rangle }{E_{n}-E_{m}}}{\Biggr ]}\\+\sum _{m'}&{\Biggl [}{\frac {\langle m'|\lambda {\hat {\boldsymbol {L}}}_{j}\cdot {\hat {\boldsymbol {S}}}_{j}|m\rangle 2J(m'nn'n){\hat {\boldsymbol {S}}}_{i}\cdot {\hat {\boldsymbol {S}}}_{j}}{E_{n'}-E_{m'}}}\\&+{\frac {2J(n'nm'n){\hat {\boldsymbol {S}}}_{i}\cdot {\hat {\boldsymbol {S}}}_{j}\langle m'|\lambda {\hat {\boldsymbol {L}}}_{j}\cdot {\hat {\boldsymbol {S}}}_{j}|n'\rangle }{E_{n'}-E_{m'}}}{\Biggr ]}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3311f79650774574764b3c11d1447f0cf4d3ff2b)






![{\displaystyle {\begin{aligned}\delta E&=2\lambda \sum \limits _{m}{\frac {J(nn'mn')}{E_{n}-E_{m}}}\langle n|{\boldsymbol {L_{i}}}|m\rangle \cdot [{\boldsymbol {S_{i}}},({\boldsymbol {S_{i}}}\cdot {\boldsymbol {S_{j}}})]\\&+2\lambda \sum _{m'}{\frac {J(nn'nm')}{E_{n'}-E_{m'}}}\langle n'|{\boldsymbol {L_{j}}}|m'\rangle \cdot [{\boldsymbol {S_{j}}},({\boldsymbol {S_{i}}}\cdot {\boldsymbol {S_{j}}})]\\&=2i\lambda \sum \limits _{m,m'}\left[{\frac {J(nn'mn')}{E_{n}-E_{m}}}\langle n|{\boldsymbol {L_{i}}}|m\rangle -{\frac {J(nn'nm')}{E_{n'}-E_{m'}}}\langle n'|{\boldsymbol {L_{j}}}|m'\rangle \right]\cdot [{\boldsymbol {S_{i}}}\times {\boldsymbol {S_{j}}}]\\&={\boldsymbol {D}}_{ij}\cdot [{\boldsymbol {S}}_{i}\times {\boldsymbol {S}}_{j}].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/287961de51b8aecdb8b7492e2fd9fe615af4b773)































