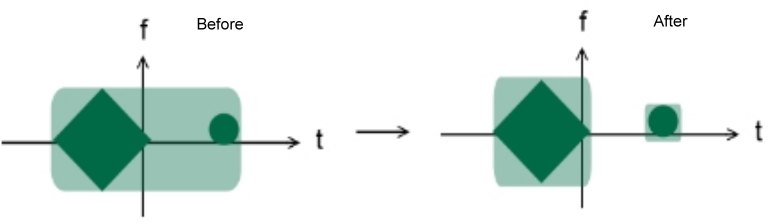
жҷӮй–“е‘Ёжіўж•°и§ЈжһҗжҰӮиҰҒдҝЎеҸ·еҮҰзҗҶгҒ«гҒҠгҒ„гҒҰ1ж¬Ўе…ғдҝЎеҸ·гӮ’гҒқгҒ®гҒҫгҒҫи§ЈжһҗгҒҷгӮӢе ҙеҗҲгҖҒгҒқгҒ®гғүгғЎгӮӨгғігҒҜе®ҹз·ҡгҒЁгҒӘгӮӢгҒҢгҖҒжҷӮй–“е‘Ёжіўж•°и§ЈжһҗгҒҜйҒ©еҪ“гҒӘеӨүжҸӣгӮ’е…ғгҒ®дҝЎеҸ·гҒ«гҒӢгҒ‘гҒҹгӮӮгҒ®пјҲгӮ„гҒҜгӮҠ1еӨүж•°й–ўж•°гҖҒгғүгғЎгӮӨгғігҒҜе®ҹз·ҡпјүгҒЁе…ғгҒ®дҝЎеҸ·гҒЁгӮ’зө„гҒҝеҗҲгӮҸгҒӣгӮӢгҒ“гҒЁгҒ«гӮҲгӮҠгҖҒе№ійқўгӮ’гғүгғЎгӮӨгғігҒЁгҒҷгӮӢ2ж¬Ўе…ғдҝЎеҸ·гӮ’з”ҹжҲҗгҒ—гҖҒи§ЈжһҗгҒ®еҜҫиұЎгҒЁгҒҷгӮӢ[1][2]гҖӮ жҷӮй–“е‘Ёжіўж•°и§ЈжһҗгҒҜйқһе®ҡеёёдҝЎеҸ·гҒ®е‘Ёжіўж•°и§ЈжһҗгҒӘгҒ©гӮ’зӣ®зҡ„гҒЁгҒҷгӮӢпјҲвҮ’ #еӢ•ж©ҹпјүгҖӮе…ёеһӢзҡ„гҒ«гҒҜжҷӮй–“й ҳеҹҹгҒ®дҝЎеҸ·гӮ’е‘Ёжіўж•°жҲҗеҲҶгҒ®жҷӮй–“еӨүеҢ–гҒ«еӨүжҸӣгҒ—гҒҰеҲҶжһҗгҒ—[3]гҖҒдёҖдҫӢгҒЁгҒ—гҒҰзҹӯжҷӮй–“гғ•гғјгғӘгӮЁеӨүжҸӣгӮ„гӮҰгӮ§гғјгғ–гғ¬гғғгғҲеӨүжҸӣгҒҢжҢҷгҒ’гӮүгӮҢгӮӢпјҲвҮ’ #жҷӮй–“е‘Ёжіўж•°еҲҶеёғй–ўж•°пјүгҖӮгҒ“гӮҢгӮүгҒҜж§ҳгҖ…гҒӘз”ЁйҖ”гҒ§еҲ©з”ЁгҒ•гӮҢгҒҰгҒ„гӮӢпјҲвҮ’ #з”ЁйҖ”пјүгҖӮжҷӮй–“е‘Ёжіўж•°и§ЈжһҗгҒ«гҒҜй•·гҒ„жӯҙеҸІгҒҢгҒӮгӮӢпјҲвҮ’ #жӯҙеҸІпјүгҖӮ еӢ•ж©ҹйқһе®ҡеёёдҝЎеҸ·гҒ®е‘Ёжіўж•°и§ЈжһҗжҷӮй–“е‘Ёжіўж•°и§ЈжһҗгҒ®зӣ®зҡ„гҒ®1гҒӨгҒ«йқһе®ҡеёёдҝЎеҸ·гҒ®е‘Ёжіўж•°и§ЈжһҗгҒҢгҒӮгӮӢ[3]гҖӮ е‘Ёжіўж•°и§ЈжһҗгҒҜдҝЎеҸ·гҒ®е…Ёй•·гӮ’гҒІгҒЁгҒҫгҒЁгҒҫгӮҠгҒЁиҰӢеҒҡгҒ—гҖҒгҒ“гӮҢгҒҢгҒ©гҒ®гӮҲгҒҶгҒӘе‘Ёжіўж•°жҲҗеҲҶгҒ§ж§ӢжҲҗгҒ•гӮҢгӮӢгҒӢеҲҶжһҗгҒҷгӮӢгҖӮгҒ“гӮҢгҒҜдҝЎеҸ·гҒҢе…Ёй•·гҒ«жёЎгҒЈгҒҰе®ҡеёёгҒ§гҒӮгӮӢгҒ“гҒЁгӮ’жҡ—зӨәзҡ„еүҚжҸҗгҒЁгҒ—гҒҰгҒ„гӮӢгҖӮгҒ—гҒӢгҒ—зҸҫе®ҹгҒ®еӨҡгҒҸгҒ®дҝЎеҸ·гҒҜйқһе®ҡеёёзҡ„гғ»жә–е®ҡеёёзҡ„гҒ§гҒӮгӮӢпјҲдҫӢ: йҹіеЈ°[4]гҖҒйҹіжҘҪпјҲжёӣиЎ°жӯЈејҰжіўпјүгҖҒз”»еғҸгҖҒеҢ»з”ЁдҝЎеҸ·гҖӮи©ізҙ°гҒҜ#з”ЁйҖ”пјүгҖӮгҒқгҒ®гҒҹгӮҒгҒ“гӮҢгӮүдҝЎеҸ·гӮ’е‘Ёжіўж•°и§ЈжһҗгҒ—гҒҰгӮӮжҲҗеҲҶгҒ®жҷӮй–“зҡ„еӨүеҢ–гҒҜеҲҶжһҗгҒ§гҒҚгҒӘгҒ„гҖӮ жҷӮй–“е‘Ёжіўж•°иЎЁзҸҫгҒҜжҷӮй–“зҡ„гҒ«еұҖеңЁгҒ—гҒҹдҝЎеҸ·гӮ’е‘Ёжіўж•°й ҳеҹҹгҒ§иЎЁзҸҫгҒ—гҖҒеҲҘгҒ®еҢәй–“гҒ§гӮӮеҗҢж§ҳгҒ®иЎЁзҸҫгӮ’гҒҷгӮӢгҖӮгҒ“гӮҢгҒ«гӮҲгӮҠгҖҒжҷӮй–“е‘Ёжіўж•°и§ЈжһҗгҒ§гҒҜжҷӮй–“зҡ„гҒ«е‘Ёжіўж•°зү№жҖ§гҒҢеӨүеҢ–гҒҷгӮӢгӮҲгҒҶгҒӘдҝЎеҸ·гӮ’жүұгҒҲгӮӢгҖӮ гҒҹгҒЁгҒҲгҒ°гҖҒж¬ЎгҒ®дҝЎеҸ·гӮ’жҷӮй–“гҒ«гӮҲгҒЈгҒҰе‘Ёжіўж•°гҒҢеӨүеҢ–гҒҷгӮӢдҝЎеҸ·гҒЁгҒ—гҒҰиЎЁзҸҫгҒ§гҒҚгӮӢгҖӮ гҒҫгҒҹгҖҒйқһеұҖжүҖзҡ„гғ•гғјгғӘгӮЁи§ЈжһҗгҒ«гӮҲгӮӢжҢҜе№…гҒӢгӮүгҒҜж¬ЎгҒ®дәҢгҒӨгҒ®дҝЎеҸ·гӮ’еҢәеҲҘгҒҷгӮӢгҒ“гҒЁгҒҢгҒ§гҒҚгҒӘгҒ„гҖӮ жҷӮй–“е‘Ёжіўж•°и§ЈжһҗгҒ§гҒҜгҒ“гӮҢгӮүгҒ®дҝЎеҸ·гҒҜеҢәеҲҘгҒ§гҒҚгӮӢгҖӮ ж•°еӯҰзҡ„еӢ•ж©ҹгҒ“гҒ®и§ЈжһҗжүӢжі•гҒ®ж•°еӯҰзҡ„гҒӘеӢ•ж©ҹд»ҳгҒ‘гҒЁгҒ—гҒҰгҖҒгҒӮгӮӢй–ўж•°гҒЁгҒқгҒ®еӨүжҸӣиЎЁзҸҫгҒЁгҒҜз·ҠеҜҶгҒ«й–ўдҝӮгҒ—гҒӮгҒЈгҒҰгҒҠгӮҠгҖҒгҒ“гӮҢгӮүгӮ’гҒқгӮҢгҒһгӮҢеҚҳзӢ¬гҒ«и§ЈжһҗгҒҷгӮӢгӮҲгӮҠгӮӮзө„гҒҝеҗҲгӮҸгҒӣгҒҰ2ж¬Ўе…ғзҡ„гҒӘеҜҫиұЎгҒЁгҒ—гҒҰи§ЈжһҗгҒҷгӮӢгҒ»гҒҶгҒҢгӮҲгӮҠиүҜгҒҸеҜҫиұЎгӮ’зҗҶи§ЈгҒ§гҒҚгӮӢгҒ“гҒЁгҒҢжҢҷгҒ’гӮүгӮҢгӮӢ[иҰҒеҮәе…ё]гҖӮеҚҳзҙ”гҒӘдҫӢгҒЁгҒ—гҒҰгҖҒгғ•гғјгғӘгӮЁеӨүжҸӣгҒ®4еӣһе‘ЁжңҹжҖ§[иЁіиӘһз–‘е•ҸзӮ№]гҖҒгҒҠгӮҲгҒігғ•гғјгғӘгӮЁеӨүжҸӣгӮ’2еӣһйҒ©з”ЁгҒҷгӮӢгҒЁж–№еҗ‘гҒҢйҖҶи»ўгҒҷгӮӢгҒ“гҒЁгҒҜгҖҒгғ•гғјгғӘгӮЁеӨүжҸӣгӮ’жҷӮй–“гғ»е‘Ёжіўж•°е№ійқўдёҠгҒ®90В°еӣһи»ўгҒ§гҒӮгӮӢгҒЁиҖғгҒҲгӮӢгҒ“гҒЁгҒ«гӮҲгӮҠгҖҒ4еӣһгғ•гғјгғӘгӮЁеӨүжҸӣгӮ’йҒ©з”ЁгҒҷгӮӢгҒЁе…ғгҒ«жҲ»гӮӢгҒ“гҒЁгҖҒгҒҠгӮҲгҒі2еӣһйҒ©з”ЁгҒҷгӮӢгҒЁ180В°еӣһи»ўгҖҒгҒҷгҒӘгӮҸгҒЎе…ғгҒ®еҗ‘гҒҚгҒЁйҖҶгҒ«гҒӘгӮӢгҒ“гҒЁгҒҢе®№жҳ“гҒ«зҗҶи§ЈгҒ§гҒҚгӮӢгҖӮ гҒқгҒ®д»–гҒ®еӢ•ж©ҹгғ•гғјгғӘгӮЁеӨүжҸӣгӮ’жӢЎејөгҒҷгӮӢгҒ“гҒЁгҒ«гӮҲгӮҠгҖҒеӨүеҢ–гҒ®йҒ…гҒ„д»»ж„ҸгҒ®еұҖжүҖеҸҜз©ҚеҲҶгҒӘдҝЎеҸ·гҒ®е‘Ёжіўж•°иЎЁзҸҫгӮ’еҫ—гӮүгӮҢгӮӢгҒҢгҖҒгҒ“гҒ®гӮўгғ—гғӯгғјгғҒгҒҜдҝЎеҸ·гҒ®жҢҒз¶ҡжҷӮй–“е…ЁдҪ“гҒ®е®Ңе…ЁгҒӘиЁҳиҝ°гӮ’дәӢеүҚгҒ«еҝ…иҰҒгҒЁгҒҷгӮӢгҖӮе®ҹйҡӣгҖҒе‘Ёжіўж•°з©әй–“дёҠгҒ®зӮ№зҫӨгӮ’жҷӮй–“з©әй–“е…ЁдҪ“гҒӢгӮүеҫ—гӮүгӮҢгҒҹжғ…е ұгӮ’гҒјгӮ„гҒ‘гҒҹеҪўгҒ§жҢҒгҒЈгҒҰгҒ„гӮӢгҒЁиҖғгҒҲгӮӢгҒ“гҒЁгҒҢгҒ§гҒҚгӮӢгҖӮж•°еӯҰзҡ„гҒ«гҒҜгӮЁгғ¬гӮ¬гғігғҲгҒ гҒҢгҖҒгҒқгҒ®гӮҲгҒҶгҒӘжүӢжі•гҒҜе°ҶжқҘгҒ®гҒөгӮӢгҒҫгҒ„гҒҢдёҚзўәе®ҡгҒӘдҝЎеҸ·гҒ®и§ЈжһҗгӮ’иЎҢгҒҶгҒ«гҒҜдёҚйҒ©еҪ“гҒ§гҒӮгӮӢгҖӮгҒҹгҒЁгҒҲгҒ°гҖҒйӣ»ж°—йҖҡдҝЎгӮ·гӮ№гғҶгғ гҒҢйқһгӮјгғӯгӮЁгғігғҲгғӯгғ”гғјгӮ’йҒ”жҲҗгҒҷгӮӢгҒҹгӮҒгҒ«гҒҜгҖҒжңӘжқҘгҒ«гҒҠгҒ‘гӮӢгҒӮгӮӢзЁӢеәҰгҒ®дёҚзўәе®ҡжҖ§гӮ’еүҚжҸҗгҒЁгҒҷгӮӢеҝ…иҰҒгҒҢгҒӮгӮӢпјҲж¬ЎгҒ«дҪ•гҒҢжқҘгӮӢгҒ®гҒӢдәӢеүҚгҒ«гӮҸгҒӢгҒЈгҒҰгҒ„гӮӢе ҙеҗҲгҖҒжғ…е ұгҒҢдјқйҒ”гӮ’иЎҢгҒҶгҒ“гҒЁгҒҜгҒ§гҒҚгҒӘгҒ„пјү[иҰҒеҮәе…ё]гҖӮ жҷӮй–“е‘Ёжіўж•°еҲҶеёғй–ўж•°жҷӮй–“е‘Ёжіўж•°еҲҶеёғгҒ®е®ҡејҸеҢ–пјҲгҒӮгӮӢгҒ„гҒҜжҷӮй–“е‘Ёжіўж•°иЎЁзҸҫпјүгҒЁгҒ—гҒҰд»ҘдёӢгҒҢжҢҷгҒ’гӮүгӮҢгӮӢпјҡ
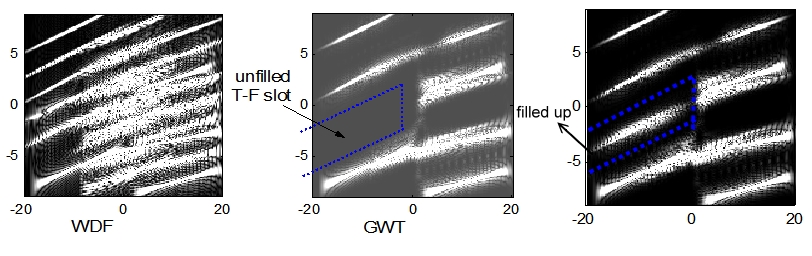
гҒ“гӮҢгӮүй–ўж•°гҒҜд»ҘдёӢгҒ®гӮҲгҒҶгҒӘзү№жҖ§е·®гҒҢгҒӮгӮӢ[5]пјҡ
зҗҶжғізҡ„гҒ«гҒҜй«ҳеҲҶи§ЈиғҪгҒ§гҖҒдәӨеҸүй …гҒҢз„ЎгҒҸгҖҒж•°еӯҰзҡ„жҖ§иіӘгҒҢиүҜгҒҸгҖҒиЁҲз®—иӨҮйӣ‘еәҰгҒҢдҪҺгҒ„гӮӮгҒ®гҒҢиүҜгҒ„гҖӮгӮҰгӮЈгӮ°гғҠгғјеҲҶеёғй–ўж•°гҒҜгҖҒгҒқгҒ®е®ҡејҸеҢ–гҒ«иҮӘе·ұзӣёй–ўй–ўж•°гӮ’еҗ«гӮҖгҒҹгӮҒгҖҒеҲҶи§ЈиғҪгҒҜй«ҳгҒ„гҒҢдәӨеҸүй …гҒҢе•ҸйЎҢгӮ’иө·гҒ“гҒҷе ҙеҗҲгҒҢгҒӮгӮӢ[иҰҒеҮәе…ё]гҖӮгҒқгҒ®гҒҹгӮҒгҖҒеҚҳй …дҝЎеҸ·гӮ’и§ЈжһҗгҒ—гҒҹгҒ„е ҙеҗҲгҒ«гҒҜгӮҰгӮЈгӮ°гғҠгғјеҲҶеёғй–ўж•°гҒҢжңҖйҒ©гҒ®гӮўгғ—гғӯгғјгғҒгҒЁгҒӘгӮӢ[иҰҒеҮәе…ё]гҖӮдҝЎеҸ·гҒҢиӨҮж•°гҒ®жҲҗеҲҶгҒӢгӮүжҲҗгӮӢе ҙеҗҲгҒ«гҒҜгҖҒгӮ¬гғңгғјгғ«еӨүжҸӣгӮ„гӮ¬гғңгғјгғ«гғ»гӮҰгӮЈгӮ°гғҠгғјеҲҶеёғй–ўж•°гҖҒдҝ®жӯЈгғҷгғјгӮҝеҲҶеёғй–ўж•°гҒӘгҒ©гҒ®еҲҘгҒ®гӮўгғ—гғӯгғјгғҒгӮ’йҒёгӮ“гҒ ж–№гҒҢгӮҲгҒ„[иҰҒеҮәе…ё]гҖӮ жҷӮй–“е‘Ёжіўж•°еҲҶеёғй–ўж•°гҒ®йҒёжҠһеҹәжә–гҒ®1гҒӨгҒҜеҲҶжһҗзӣ®зҡ„пјҲз”ЁйҖ”пјүгҒ§гҒӮгӮӢ[6]гҖӮд»–гҒ®еҹәжә–гҒЁгҒ—гҒҰдҝЎеҸ·гҒқгҒ®гӮӮгҒ®пјҲ=дҝЎеҸ·жЁҷжң¬гҒ«еҗҲгҒЈгҒҹй–ўж•°гӮ’йҒёгҒ¶пјүгҒҢгҒӮгӮӢ[7]гҖӮ з”ЁйҖ”д»ҘдёӢгҒ®з”ЁйҖ”гҒҜжҷӮй–“е‘Ёжіўж•°еҲҶеёғй–ўж•°гҒ®йҒёжҠһгҒЁдҝЎеҸ·еҮҰзҗҶгӮ’иҰҒгҒҷгӮӢгҖӮ зһ¬жҷӮе‘Ёжіўж•°жҺЁе®ҡзһ¬жҷӮе‘Ёжіўж•°гҒҜзһ¬жҷӮдҪҚзӣё гҒ®жҷӮй–“еӨүеҢ–зҺҮгҒ§гҒӮгӮҠгҖҒд»ҘдёӢгҒ®ејҸгҒ§е®ҡзҫ©гҒ•гӮҢгӮӢпјҡ еғҸгҒҢй®®жҳҺгҒ§гҒӮгӮҢгҒ°жҷӮй–“е‘Ёжіўж•°иЎЁзҸҫгҒӢгӮүзӣҙжҺҘзһ¬жҷӮе‘Ёжіўж•°гӮ’зҹҘгӮӢгҒ“гҒЁгҒҢгҒ§гҒҚгӮӢ[иҰҒеҮәе…ё]гҖӮй®®жҳҺгҒ•гҒҢйҮҚиҰҒгҒ§гҒӮгӮҠгӮҰгӮЈгӮ°гғҠгғјеҲҶеёғй–ўж•°гҒҢеӨҡз”ЁгҒ•гӮҢгӮӢ[иҰҒеҮәе…ё]гҖӮ гғ•гӮЈгғ«гӮҝгғӘгғігӮ°гҒЁдҝЎеҸ·еҲҶи§Ј 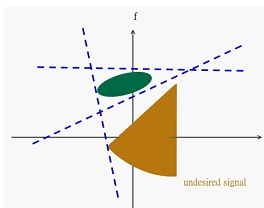 гғ•гӮЈгғ«гӮҝгғӘгғігӮ°гҒ®зӣ®зҡ„гҒҜжңӣгҒҫгҒ—гҒҸгҒӘгҒ„дҝЎеҸ·жҲҗеҲҶгҒ®йҷӨеҺ»гҒ§гҒӮгӮҠгҖҒдҝЎеҸ·еҲҶи§ЈгҒ®зӣ®зҡ„гҒҜдҝЎеҸ·жҲҗеҲҶгҒ®иүҜгҒ„еҲҶйӣўгҒ§гҒӮгӮӢгҖӮгҒ“гӮҢгӮүгҒ®гҒҹгӮҒгҒ«гҖҒеҸӨе…ёзҡ„гҒ«гҒҜжҷӮй–“й ҳеҹҹгҒӮгӮӢгҒ„гҒҜе‘Ёжіўж•°й ҳеҹҹгҒ§зӢ¬з«ӢгҒ—гҒҰгғ•гӮЈгғ«гӮҝгғјгҒҢйҒ©з”ЁгҒ•гӮҢгӮӢпјҲеӣіеҸӮз…§пјүгҖӮгҒ—гҒӢгҒ—гҒ“гҒ®жүӢжі•гҒҜжҷӮеӨүгҒ®е‘Ёжіўж•°жҲҗеҲҶгӮ’еҲҶйӣўгҒ§гҒҚгҒӘгҒ„пјҲеӣіеҸӮз…§пјүгҖӮ жҷӮй–“е‘Ёжіўж•°еҲҶжһҗгҒ«гӮҲгӮҠгҖҒгғҰгғјгӮҜгғӘгғғгғүзҡ„жҷӮй–“е‘Ёжіўж•°гғүгғЎгӮӨгғігҒ«гҒӨгҒ„гҒҰгҖҒгӮӮгҒ—гҒҸгҒҜеҲҶж•°ж¬Ўгғ•гғјгғӘгӮЁеӨүжҸӣгҒ«гӮҲгӮҠеҲҶж•°ж¬ЎгғүгғЎгӮӨгғігҒ«гҒӨгҒ„гҒҰгғ•гӮЈгғ«гӮҝгӮ’йҒ©з”ЁгҒ§гҒҚгӮӢгҖӮгғ•гӮЈгғ«гӮҝгҒ®иЁӯиЁҲгҒҜеёёгҒ«иӨҮж•°жҲҗеҲҶгҒӢгӮүгҒӘгӮӢиӨҮж•°гҒ®дҝЎеҸ·гӮ’жүұгҒҶгҒҹгӮҒгҖҒдәӨеҸүй …гҒ®гҒӮгӮӢгӮҰгӮЈгӮ°гғҠгғјй–ўж•°гӮ’з”ЁгҒ„гӮӢгҒ“гҒЁгҒҜгҒ§гҒҚгҒҡ[иҰҒеҮәе…ё]гҖҒгӮ¬гғңгғјгғ«еӨүжҸӣгҖҒгӮ¬гғңгғјгғ«гғ»гӮҰгӮЈгӮ°гғҠгғјеҲҶеёғй–ўж•°гӮӮгҒ—гҒҸгҒҜCohenгӮҜгғ©гӮ№еҲҶеёғй–ўж•°гҒӘгҒ©гӮ’дҪҝгҒҶгҒ“гҒЁгҒҢгҒ§гҒҚгӮӢ[иҰҒеҮәе…ё]гҖӮ жЁҷжң¬еҢ–е®ҡзҗҶгғҠгӮӨгӮӯгӮ№гғҲгғ»гӮ·гғЈгғҺгғігҒ®жЁҷжң¬еҢ–е®ҡзҗҶгҒ«гӮҲгӮҠгҖҒгӮЁгӮӨгғӘгӮўгӮ№гӮ’з”ҹгҒҳгҒ•гҒӣгҒӘгҒ„гҒҹгӮҒгҒ«еҝ…иҰҒгҒӘжЁҷжң¬зӮ№гҒ®ж•°гҒҜгҖҒдҝЎеҸ·гҒ®жҷӮй–“е‘Ёжіўж•°еҲҶеёғгҒ®йқўз©ҚгҒЁзӯүгҒ—гҒ„гҒ“гҒЁгҒҢиЁҖгҒҲгӮӢ[иҰҒеҮәе…ё]пјҲгҒ“гӮҢгҒҜе®ҹйҡӣгҒ«гҒҜиҝ‘дјјгҒ§гҒӮгӮӢгҖӮд»»ж„ҸгҒ®дҝЎеҸ·гҒ®жҷӮй–“е‘Ёжіўж•°йқўз©ҚгҒҜе®ҹйҡӣгҒ«гҒҜз„ЎйҷҗеӨ§гҒ§гҒӮгӮӢпјүгҖӮжЁҷжң¬еҢ–е®ҡзҗҶгӮ’жҷӮй–“е‘Ёжіўж•°еҲҶеёғгҒЁзө„гҒҝеҗҲгӮҸгҒӣгӮӢеүҚгҒЁеҫҢгҒ«гҒӨгҒ„гҒҰгҒ®дҫӢгӮ’д»ҘдёӢгҒ«зӨәгҒҷгҖӮ жҷӮй–“е‘Ёжіўж•°еҲҶеёғгӮ’йҒ©з”ЁгҒҷгӮӢгҒЁжЁҷжң¬зӮ№гҒ®ж•°гҒҢжёӣгӮӢгҒ“гҒЁгҒҜзү№зӯҶгҒ«дҫЎгҒҷгӮӢгҖӮ гӮҰгӮЈгӮ°гғҠгғјеҲҶеёғй–ўж•°гҒ§гҒҜдәӨеҸүй …пјҲе№ІжёүгҒЁгӮӮпјүгҒ®е•ҸйЎҢгҒҢгҒӮгӮҠгҒҶгӮӢ[иҰҒеҮәе…ё]гҖӮгӮ¬гғңгғјгғ«еӨүжҸӣгҒ®е ҙеҗҲгҖҒиЎЁзҸҫгҒ®й®®жҳҺгҒ•гҒЁеҸҜиӘӯжҖ§гҒҢеҗ‘дёҠгҒ—дҝЎеҸ·гҒ®и§ЈйҮҲгҒҠгӮҲгҒіе®ҹи·өзҡ„е•ҸйЎҢгҒёгҒ®еҝңз”ЁеҸҜиғҪжҖ§гӮӮеҗ‘дёҠгҒҷгӮӢ[иҰҒеҮәе…ё]гҖӮзөҗжһңгҒЁгҒ—гҒҰгҖҒеҚҳдёҖжҲҗеҲҶгҒӢгӮүжҲҗгӮӢдҝЎеҸ·гӮ’жЁҷжң¬еҢ–гҒҷгӮӢе ҙеҗҲгҒ«гҒҜгӮҰгӮЈгӮ°гғҠгғјеҲҶеёғй–ўж•°гҒҢз”ЁгҒ„гӮүгӮҢгҖҒиӨҮж•°гҒ®жҲҗеҲҶгҒӢгӮүжҲҗгӮӢдҝЎеҸ·гҒ«еҜҫгҒ—гҒҰгҒҜгӮ¬гғңгғјгғ«еӨүжҸӣгӮ„гӮ¬гғңгғјгғ«гғ»гӮҰгӮЈгӮ°гғҠгғјеҲҶеёғй–ўж•°гҒӘгҒ©гҒ®е№ІжёүгҒҢжҠ‘гҒҲгӮүгӮҢгӮӢжҷӮй–“е‘Ёжіўж•°еҲҶеёғгҒҢз”ЁгҒ„гӮүгӮҢгӮӢ[иҰҒеҮәе…ё]гҖӮгғҗгғӘгӮўгғігғ»гғӯгӮҰгҒ®е®ҡзҗҶгҒҜгҒ“гҒ®гҒ“гҒЁгӮ’е®ҡејҸеҢ–гҒ—гҒҰгҒҠгӮҠгҖҒеҝ…иҰҒжңҖдҪҺйҷҗгҒ®жҷӮй–“е‘Ёжіўж•°жЁҷжң¬ж•°гӮ’дёҺгҒҲгӮӢгҖӮ еӨүиӘҝгҒҠгӮҲгҒіеӨҡйҮҚеҢ–еҸӨе…ёзҡ„гҒӘеӨүиӘҝгҒЁеӨҡйҮҚеҢ–гҒҜжҷӮй–“й ҳеҹҹгҒӮгӮӢгҒ„гҒҜе‘Ёжіўж•°й ҳеҹҹеҚҳдҪ“гҒ§жүұгӮҸгӮҢгҒҰгҒ„гҒҹгҖӮжҷӮй–“е‘Ёжіўж•°еҲҶеёғгӮ’жҙ»з”ЁгҒ—гҖҒжҷӮй–“е‘Ёжіўж•°е№ійқўгҒ®йҡҷй–“гӮ’еҹӢгӮҒгӮӢгҒ“гҒЁгҒ«гӮҲгӮҠеӨүиӘҝгҒҠгӮҲгҒіеӨҡйҮҚеҢ–гӮ’гӮҲгӮҠеҠ№зҺҮзҡ„гҒ«иЎҢгҒҲгӮӢ[иҰҒеҮәе…ё]гҖӮд»ҘдёӢгҒ«дҫӢгӮ’зӨәгҒҷпјҲдҫӢгҒ®гҒЁгҒҠгӮҠгҖҒгӮҰгӮЈгӮ°гғҠгғјеҲҶеёғй–ўж•°гҒҜдәӨеҸүй …гҒ®е•ҸйЎҢгҒҢи‘—гҒ—гҒҸгҖҒгҒ“гҒ®з”ЁйҖ”гҒ«гҒҜйҒ©гҒ•гҒӘгҒ„пјүгҖӮ йӣ»зЈҒжіўгҒ®дјқж’ӯйӣ»зЈҒжіўгҒҜ2Г—1иЎҢеҲ—гҒ®еҪўгҒ«иЎЁгӮҸгҒҷгҒ“гҒЁгҒҢгҒ§гҒҚгӮӢгҖӮ гҒ“гӮҢгҒҜжҷӮй–“е‘Ёжіўж•°е№ійқўгҒЁдјјгҒҰгҒ„гӮӢгҖӮиҮӘз”ұз©әй–“гӮ’дјқж’ӯгҒҷгӮӢйӣ»зЈҒжіўгҒ«гҒҜгғ•гғ¬гғҚгғ«еӣһжҠҳгҒҢиө·гҒ“гӮӢгҖӮгҒ“гӮҢгҒҜ2Г—1иЎҢеҲ— гҒ«гғ‘гғ©гғЎгғјгӮҝиЎҢеҲ— пјҲгҒ“гҒ“гҒ§ z гҒҜдјқж’ӯи·қйӣўгӮ’гҖҒО» гҒҜжіўй•·гӮ’иЎЁгӮҸгҒҷпјүгҒ®LCTгӮ’дҪңз”ЁгҒ•гҒӣгӮӢгҒ“гҒЁгҒ§иЎЁзҸҫгҒ§гҒҚгӮӢ[иҰҒеҮәе…ё]гҖӮйӣ»зЈҒжіўгҒҢзҗғйқўгғ¬гғігӮәйҖҡйҒҺгӮӮгҒ—гҒҸгҒҜеҶҶзӣӨгҒ«гӮҲгӮҠеҸҚе°„гҒ•гӮҢгӮӢгҒЁгҒҚгҖҒгғ‘гғ©гғЎгғјгӮҝиЎҢеҲ—гҒҜгҒқгӮҢгҒһгӮҢд»ҘдёӢгҒ®гӮҲгҒҶгҒ«гҒӘгӮӢгҖӮ гҒ“гҒ“гҒ§ f гҒҜгғ¬гғігӮәгҒ®з„ҰзӮ№и·қйӣўгӮ’гҖҒR гҒҜеҶҶзӣӨгҒ®еҚҠеҫ„гӮ’иЎЁгӮҸгҒҷгҖӮгҒқгҒ®зөҗжһңгҒҜд»ҘдёӢгҒ®гӮҲгҒҶгҒӘеҪўејҸгҒ§еҫ—гӮүгӮҢгӮӢгҖӮ з·ҡеҪўжӯЈжә–еӨүжҸӣз·ҡеҪўжӯЈжә–еӨүжҸӣ(LCT)гҒҜжңүз”ЁгҒ§гҖҒжҷӮй–“е‘Ёжіўж•°е№ійқўдёҠгҒ®дҝЎеҸ·еҪўгӮ’д»»ж„ҸеҪўзҠ¶гҒ«еӨүжҸӣгҒ§гҒҚгӮӢ[иҰҒеҮәе…ё]гҖӮгҒҹгҒЁгҒҲгҒ°гҖҒд»»ж„ҸдҪҚзҪ®гҒёгҒ®з§»еӢ•гҖҒйқўз©ҚгӮ’дҝқгҒЈгҒҹдјёзё®гҖҒеӮҫж–ң[иЁіиӘһз–‘е•ҸзӮ№]гҖҒеӣһи»ўпјҲеҲҶж•°ж¬Ўгғ•гғјгғӘгӮЁеӨүжҸӣпјүгҒӘгҒ©гҒҢеҸҜиғҪгҒ§гҒӮгӮӢгҖӮ гҒқгҒ®д»–гҒ®еҝңз”ЁжҷӮй–“е‘Ёжіўж•°и§ЈжһҗгҒҜе·ҘеӯҰзҡ„гҒ«еәғгҒҸеҝңз”ЁгҒ•гӮҢгӮӢгҖӮд»ҘдёӢгҒҜгҒқгҒ®дёҖдҫӢгҒ§гҒӮгӮӢпјҡ
жӯҙеҸІ
жҷӮй–“е‘Ёжіўж•°и§ЈжһҗгҒ«й–ўгҒҷгӮӢеҲқжңҹгҒ®жҘӯзёҫгҒЁгҒ—гҒҰгҖҒгғҸгғјгғ«гғ»гӮўгғ«гғ•гғ¬гғғгғүгҒ®гғҸгғјгғ«гӮҰгӮ§гғјгғ–гғ¬гғғгғҲ(1909)гҒҢжҢҷгҒ’гӮүгӮҢгӮӢгҖӮгҒ—гҒӢгҒ—гҖҒгҒ“гӮҢгҒҜдҝЎеҸ·еҮҰзҗҶгҒ«гҒӮгҒҫгӮҠйҒ©з”ЁгҒ•гӮҢгӮӢгҒ“гҒЁгҒҜгҒӘгҒӢгҒЈгҒҹгҖӮгӮҲгӮҠеҪұйҹҝгҒ®еӨ§гҒҚгҒ„жҘӯзёҫгҒЁгҒ—гҒҰгӮ¬гғјгғңгғ«гғ»гғҮгғјгғҚгӮ·гғҘгҒ«гӮҲгӮӢеҲқжңҹгҒ®гӮҰгӮ§гғјгғ–гғ¬гғғгғҲгҒЁиЁҖгҒҲгӮӢGabor atom (1947)гӮ„зҹӯжҷӮй–“гғ•гғјгғӘгӮЁеӨүжҸӣгӮ’дҝ®жӯЈгҒ—гҒҹгӮ¬гғңгғјгғ«еӨүжҸӣгҒҢжҢҷгҒ’гӮүгӮҢгӮӢгҖӮгӮёгғЈгғігғ»гғ“гғ¬дҝЎеҸ·еҮҰзҗҶгҒ®ж–Үи„ҲгҒ«е°Һе…ҘгҒ—гҒҹгӮҰгӮЈгӮ°гғҠгғјгғ»гғ“гғ¬еҲҶеёғ(1948)гӮӮеҹәзӣӨзҡ„жҘӯзёҫгҒЁгҒ—гҒҰжҢҷгҒ’гӮүгӮҢгӮӢгҖӮ зү№гҒ«1930е№ҙд»ЈгҒҠгӮҲгҒі1940е№ҙд»ЈгҒ«гҒҜгҖҒеҲқжңҹгҒ®жҷӮй–“е‘Ёжіўж•°и§ЈжһҗгҒҢйҮҸеӯҗеҠӣеӯҰгҒЁжӯ©иӘҝгӮ’еҗҲгӮҸгҒӣгҒҰй–ӢзҷәгҒ•гӮҢгҒҹгҖӮгӮҰгӮЈгӮ°гғҠгғјгҒҜгӮҰгӮЈгӮ°гғҠгғјгғ»гғ“гғ¬еҲҶеёғгӮ’1932е№ҙгҒ«йҮҸеӯҗеҠӣеӯҰгҒ®еҲҶйҮҺгҒ§й–ӢзҷәгҒ—гҖҒгӮ¬гғјгғңгғ«гҒҜйҮҸеӯҗеҠӣеӯҰгҒ®еҪұйҹҝгӮ’еҸ—гҒ‘гҒҰгҒ„гҒҹгҖӮгҒ“гӮҢгҒҜдҪҚзҪ®гғ»йҒӢеӢ•йҮҸе№ійқўгҒЁжҷӮй–“гғ»е‘Ёжіўж•°е№ійқўгҒЁгҒ®й–“гҒ®ж•°еӯҰзҡ„е…ұйҖҡжҖ§гӮ’еҸҚжҳ гҒ—гҒҰгҒ„гӮӢгҖӮгҒҹгҒЁгҒҲгҒ°гҖҒйҮҸеӯҗеҠӣеӯҰгҒ«гҒҠгҒ‘гӮӢгғҸгӮӨгӮјгғігғҷгғ«гӮ°гҒ®дёҚзўәе®ҡжҖ§еҺҹзҗҶгҒҜжҷӮй–“е‘Ёжіўж•°и§ЈжһҗгҒ«гҒҠгҒ‘гӮӢгӮ¬гғңгғјгғ«йҷҗз•ҢгҒ«зӣёеҪ“гҒ—гҖҒгҒ“гӮҢгӮүгҒҜгҒ©гҒЎгӮүгӮӮ究жҘөзҡ„гҒ«гҒҜгӮ·гғігғ—гғ¬гӮҜгғҶгӮЈгғғгӮҜж§ӢйҖ гӮ’еҸҚжҳ гҒ—гҒҹгӮӮгҒ®гҒ§гҒӮгӮӢгҖӮ и„ҡжіЁжіЁйҮҲеҮәе…ё
еҸӮиҖғж–ҮзҢ®
й–ўйҖЈй …зӣ® |
Portal di Ensiklopedia Dunia