„Éõ„ÉĘ„āĮ„É™„Éč„ÉÉ„āĮŤĽĆťĀď śēįŚ≠¶„Āę„Āä„ĀĄ„Ā¶„ÄĀ„Éõ„ÉĘ„āĮ„É™„Éč„ÉÉ„āĮŤĽĆťĀď(homoclinic orbit)„Ā®„ĀĮ„ÄĀŚäõŚ≠¶Á≥Ľ„Āę„Āä„ĀĎ„āčśĶĀ„āĆ„ĀģŤĽĆŤ∑°„Āß„ÄĀťěćÁāĻÔľąsaddle pointԾȄĀč„āČŚáļ„Ā¶„ÄĀŚźĆ„ĀėťěćÁāĻ„ĀęśąĽ„Ā£„Ā¶„ĀŹ„ā荼ƝĀď„Āß„Āā„āč„Äā „āą„āäŚé≥ŚĮÜ„Āę„ÄĀťěćÁāĻ„Āß„ĀģŚģČŚģöŚ§öśßėšĹď„Ā®šłćŚģČŚģöŚ§öśßėšĹď„ĀģÁ©ćťõÜŚźą„Ā®„āāŚģöÁĺ©„Āß„Āć„āč„Äā ŚŹćŚĺ©ŚÜôŚÉŹÁ≥ĽÔľąťõĘśē£ŚäõŚ≠¶Á≥ĽÔľČ„Āß„āā„ÄĀ„Éõ„ÉĘ„āĮ„É™„Éč„ÉÉ„āĮŤĽĆťĀď„āĄ„ÄĀ„Éõ„ÉĘ„āĮ„É™„Éč„ÉÉ„āĮ„ÉĚ„ā§„É≥„Éą„ĀĮŚźĆśßė„Āę„ÄĀŚģČŚģöŚ§öśßėšĹď„Ā®šłćŚģČŚģöŚ§öśßėšĹď„ĀģšłćŚčēÁāĻ„Ā®ŚĎ®śúüÁāĻ„āíÁĒ®„ĀĄ„Ā¶ŚģöÁĺ©„Āô„āč„Āď„Ā®„ĀĆ„Āß„Āć„āč„Äā ŚĺģŚąÜśĖĻÁ®čŚľŹÁ≥Ľ„Āß„ĀģŚģöÁĺ©ś¨°„Āģ„āą„ĀÜ„Ā™ŚłłŚĺģŚąÜśĖĻÁ®čŚľŹ„ĀߌģöÁĺ©„Āē„āĆ„ĀüťÄ£Á∂öŚäõŚ≠¶Á≥Ľ„āíŤÄÉ„Āą„āč„Äā „ĀĆšłćŚčēÁāĻ„Āß„Āā„āä„ÄĀŤß£„ĀĆś¨°„āíśļÄ„Āü„Āô„Ā™„āČ„Āį„Éõ„ÉĘ„āĮ„É™„Éč„ÉÉ„āĮŤĽĆťĀď„Āß„Āā„āč„Äā „āā„Āó„ÄĀÁõłÁ©ļťĖď„ĀĆ3ś¨°ŚÖÉšĽ•šłä„Ā™„āČ„Āį„ÄĀťěćÁāĻšłä„ĀģšłćŚģČŚģöŚ§öśßėšĹď„āí„āą„ā䍩≥„Āó„ĀŹŤ™Ņ„ĀĻ„āčŚŅÖŤ¶Ā„ĀĆ„Āā„āč„Äā Ś§ßŚą•„Āó„Ā¶2„Ā§„ĀģŚ†īŚźą„Āę„Ā§„ĀĄ„Ā¶ŤŅį„ĀĻ„āč„Äā šłÄ„Ā§Áõģ„ĀĮ„ÄĀšłćŚģČŚģöŚ§öśßėšĹď„ĀĆŚĻĺšĹēŚ≠¶ÁöĄ„Āę„ĀĮŚÜÜÁ≠íŚěč„Ā®ŚźĆÁõł„Āß„Āā„ā茆īŚźą„Āß„ÄĀ šļĆ„Ā§Áõģ„ĀĮ„ÄĀšłćŚģČŚģöŚ§öśßėšĹď„ĀĆŚĻĺšĹēŚ≠¶ÁöĄ„Āę„ĀĮ„ÄĀ„É°„Éď„ā¶„āĻ„ĀģŤľ™„Ā®ŚźĆÁõł„Āß„Āā„ā茆īŚźą„Āß„Āā„āč„Äā šļĆ„Ā§Áõģ„Āģ„Éõ„ÉĘ„āĮ„É™„Éč„ÉÉ„āĮŤĽĆťĀď„āíÁČĻ„Āę„ÄĀ„Ā≠„Āė„āĆ„Ā¶„ĀĄ„āč„Ā®ŚĎľ„Ā∂„Äā ťõĘśē£ŚäõŚ≠¶Á≥Ľ„Āę„Ā§„ĀĄ„Ā¶„āā„ÄĀ„Éõ„ÉĘ„āĮ„É™„Éč„ÉÉ„āĮŤĽĆťĀď„ĀĮŚģöÁĺ©ŚŹĮŤÉĹ„Āß„Āā„āč„Äā
ŚÜôŚÉŹ„ĀĆ„ÄĀŚ§öśßėšĹď„ĀģŚĺģŚąÜŚźĆÁõł„Āß„Āā„āč„Ā®„Āć„ÄĀ
„ĀĆŚźĆ„Āėśú™śĚ•„Ā®ťĀéŚéĽ„āíśĆĀ„Ā£„Ā¶„ĀĄ„āč„ÄĀ„Ā§„Āĺ„āä„ĀĮ„ÄĀšłćŚčēÁāĻ„Āĺ„Āü„ĀĮŚĎ®śúüÁāĻ„ĀĆŚ≠ėŚú®„Āô„āč
„Āß„Āā„āč„Ā®„Āć„ÄĀ„āí„Éõ„ÉĘ„āĮ„É™„Éč„ÉÉ„āĮ„ÉĚ„ā§„É≥„Éą„Ā®ŚĎľ„Ā∂„Äā 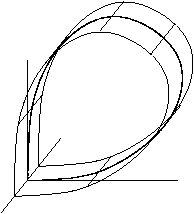 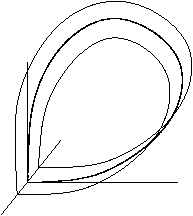 ŚŹāŤÄÉśĖáÁĆģ
Ś§ĖťÉ®„É™„É≥„āĮ
ťĖĘťÄ£ť†ÖÁõģ |
Portal di Ensiklopedia Dunia






















