លេអុនហាដ អយល័រ

**លេអុនហាដ អយល័រ**
លេអុនហាដ អយល័រ
	គំនូរ Emanuel Handmann 1756(?)
កើតនៅ	១៥ មេសា ១៧០៧; Basel, Switzerland
មរណភាព	១៨ កញ្ញា ១៧៨៣; St. Petersburg, Russia
Residence	ព្រុស្ស៊ី, រុស្ស៊ី; ស្វ៊ីស
សញ្ជាតិ	ស្វ៊ីស
ឯកទេស	គណិតវិទូ និង រូបវិទូ
Institutions	Imperial Russian Academy of Sciences; Berlin Academy
Alma mater	University of Basel
Doctoral advisor	Johann Bernoulli
Doctoral students	Nicolas Fuss; Johann Hennert; Joseph Louis Lagrange; Stepan Rumovsky
Known for	See full list
	Signature;
	Notes; គាត់ជាឪពុករបស់គណិតវិទូ Johann Euler;

លេអុនហាដ អយល័រ (អាល្លឺម៉ង់: Leonhard Euler, អានតាមអាល្លឺម៉ង់ : /ˈɔʏlɐ/;^[១] ១៥ មេសា ឆ្នាំ ១៧០៧ - ១៨ កញ្ញា ឆ្នាំ ១៧៨៣) ជាគណិតវិទូនិងរូបវិទូស្វ៊ីសដ៏ល្បីល្បាញមួយរូប។ គាត់បានស្រាវជ្រាវរកឃើញរបស់សំខាន់ៗជាច្រើនក្នុងវិស័យដ៏ទូលំទូលាយដូចជាការគណនាមិនកំណត់ (infinitesimal calculus) និងទ្រឹស្ដីក្រាប។ គាត់ក៏ជាអ្នកបង្កើតពាក្យនិងនិមិត្តសញ្ញាគណិតវិទ្យាទំនើបជាច្រើនផងដែរ ជាពិសេសសម្រាប់ផ្នែកគណិតវិភាគ ដូចជាសញ្ញាតំណាងអនុគមន៍ជាដើម។^[២] គាត់បានបង្កើតស្នាដៃល្បីៗក្នុងវិស័យមេកានិច ឌីណាមិចអង្គធាតុរាវ អុបទិចនិងតារាវិទ្យា។

អយល័របានចំណាយពេលវេលាភាគច្រើននៃជីវិតពេញវ័យរបស់គាត់រស់នៅក្នុងក្រុងសាំងពេទ័របួគ៌ ប្រទេសរុស្ស៊ី និងក្រុងប៊ែរឡាំង រាជាណាចក្រព្រុស្ស៊ីយ៉ា (សព្វថ្ងៃប្រទេសអាល្លឺម៉ង់)។ គាត់ត្រូវបានគេចាត់ទុកថាជាគណិតវិទូដ៏ល្បីបំផុតនៅក្នុងសតវត្សរ៍ទី១៨ និងអាចចាត់ទុកជាគណិតវិទូដ៏ល្បីបំផុតគ្រប់កាលសម័យ ដោយមិនអាចប្រកែកបាន។ គាត់ជាបុគ្គលដែលបានបង្កើតស្នាដៃដ៏ច្រើន; ស្នាដៃរបស់គាត់បើចងក្រងជាសៀវភៅទម្រង់ក្វារតូ(សៀវភៅទំហំ 9x12") នោះអាចមានរហូតដល់៦០ទៅ៨០ក្បាល។^[៣] លោក ព្យែរស៊ីម៉ុន ឡាប្លាស់ បានសម្ដែងពីឥទ្ធិពលរបស់លោកអយល័រក្នុងផ្នែកគណិតវិទ្យា ដោយប្រយោគមួយឃ្លាថា "អានអយល័រ, អានអយល័រ, គាត់ជាគ្រូរបស់យើងក្នុងគ្រប់វិស័យ" ដែលក្រោយមកគេសម្រួលមកជា ""អានអយល័រ, អានអយល័រ, គាត់ជាគ្រូរបស់យើងទាំងអស់គ្នា"។ ^[៤]

រូបថតអយល័រ ត្រូវបានដាក់បង្ហាញនៅលើក្រដាសប្រាក់១០ហ្វ្រង់ស៊េរីទី១០របស់ស្វ៊ីស និងនៅលើតែមជាច្រើនរបស់ប្រទេសស្វ៊ីស អាល្លឺម៉ង់ និងរុស្ស៊ី។ គេបានដាក់ឈ្មោះកូនភពមួយថា កូនភពអយល័រ២០០២ ដើម្បីជាការផ្ដល់កិត្តិយសដល់គាត់។ គាត់ក៏ត្រូវបានគេកត់បញ្ចូលដើម្បីធ្វើបុណ្យរំលឹកគុណដោយព្រះវិហារ Lutheran ទៅក្នុងប្រក្រតីទិននៃសន្តបុគ្គលក្នុងថ្ងៃ២៤ឧសភា; អយល័រជាអ្នកជឿស៊ប់លើសាសនាគ្រឹស្ទ ដែលជឿថាព្រះគម្ពីរត្រឹមត្រូវឥតខ្ចោះ ហើយបានសរសេរលិខិតជាច្រើនការពារសាសនាទប់ទល់នឹងអ្នកដែលមិនជឿលើព្រះគម្ពីរនាសម័យនោះ។^[៥]

ឆាកជីវិត

បឋមកាល

អយល័របានកើតនៅថ្ងៃទី១៥ ខែមេសា ឆ្នាំ១៧០៧ នៅបាហ្សល (Basel)។ ឪពុករបស់គាត់ឈ្មោះ ប៉ូលអយល័រ ជាប៉ាស្ទ័ររបស់ព្រះវិហារប្រូតេស្តង់។ ម្ដាយរបស់គាត់ឈ្មោះម៉ាកឺរីតប្រាក់ឃ័រ ជាកូនស្រីរបស់ប៉ាស្ទ័រម្នាក់។ គាត់មានប្អូនស្រីពីរនាក់ឈ្មោះ អាណាម៉ារីយ៉ា និង ម៉ារីយ៉ា ម៉ាក់ដាលេណា។ មួយរយៈខ្លីក្រោយកំណើតរបស់លេអុនហាដ គ្រួសារអយល័របានរើចេញពីបាហ្សលទៅរស់នៅក្រុង Riehen ដែលនៅទីនោះអយល័របានរស់នៅយ៉ាងក្នុងវ័យកុមារភាព។ ប៉ូលអយល័រជាមិត្តភក្តិរបស់គ្រួសារប៊ែរនូលី—យ៉ូហាន ប៊ែរនូលី ដែលត្រូវបានគេចាត់ទុកថាជាគណិតវិទួដ៏ល្បីបំផុតនៅអឺរ៉ុប ហើយអាចជាអ្នកដ៏មានឥទ្ធិពលម្នាក់ទៅលើយុវជនលេអុនហាដ។ អយល័របានចាប់ផ្ដើមសិក្សានៅបាហ្សល ដែលនៅទីនោះគាត់ត្រូវបានបញ្ជូនឱ្យទៅរស់នៅជាមួយយាយខាងម្ដាយ។ នៅអាយុ១៣ឆ្នាំ គាត់បានចូលរៀននៅសាកលវិទ្យាល័យបាហ្សល ហើយនៅឆ្នាំ១៧២៣ គាត់បានទទួលសញ្ញាប័ត្រថ្នាក់ម៉ាស្ទ័រផ្នែកទស្សនវិជ្ជា ដែលបរមាធិប្បាយរបស់គាត់ប្រៀបបាននឹងទស្សនវិជ្ជារបស់ដេកាត និងញូតុនដែរ។ នៅក្នុងពេលនោះ គាត់តែងទៅរៀនជាមួយយ៉ូហានប៊ែរនូលីនារៀងរាល់ល្ងាចថ្ងៃសៅរ៍។ ប៊ែរនូលីបានដឹងច្បាស់ថាកូនសិស្សរបស់គាត់មានជំនាញខាងគណិតវិទ្យា។ ^[៦] នៅពេលនោះអយល័រកំពុងសិក្សាទេវាវិទ្យា ភាសាក្រិច និងភាសាហ៊ីប្រូវ៍ (Hebrew) ក្រោមសម្ពាធពីឪពុកដើម្បីក្លាយជាប៉ាស្ទ័រ, ប៉ុន្តែប៊ែរនូលីបានជម្នះប៉ូលអយល័រថា លេអុនហាដមានវាសនាកើតមកត្រូវក្លាយជាគណិតវិទូដ៏ល្បីល្បាញមួយរូប។ នៅឆ្នាំ១៧២៦ អយល័របានបញ្ចប់សារណាលើដំណាលនៃសំឡេង ក្រោមចំណងជើងថា De Sono^[៧]. ក្នុងពេលនោះ គាត់បានដាក់បេក្ខភាពប្រកួតប្រជែងដណ្ដើមមុខតំណែងនៅសកលវិទ្យាល័យបាហ្សល តែត្រូវបរាជ័យ។ នៅឆ្នាំ១៧២៧ គាត់បានចូលរួមប្រកួតប្រជែងដណ្ដើមពានរង្វាន់ចំណោទបណ្ឌិតសភាប៉ារីស ដែលចំណោទនាសម័យនោះគឺរកវិធីដែលប្រសើរបំផុតក្នុងការដាក់ដងក្ដោងទូក។ គាត់បានឈ្នះរង្វាន់លេខ២ ដោយលេខមួយបានទៅលោក ព្យែរប៊ូគេរ(Pierre Bouguer)— ដែលគេស្គាល់ថាជាបិតានៃស្ថាបត្យកម្មនាវា។ នៅពេលក្រោយមក អយល័របានឈ្នះការប្រកួតប្រចាំឆ្នាំនេះចំនួន១២ដង។ ^[៨]

ជីវិតនៅសាំងពេទ័របួគ៌

អំលុងនោះ កូនប្រុសទាំងពីរនាក់របស់យ៉ូហានប៊ែរនូលី គឺ ដានីញែលប៊ែរនូលី និង នីកូឡាប៊ែរនូលី កំពុងតែធ្វើការនៅបណ្ឌិតសភាវិទ្យាសាស្ត្រចក្រភពរុស្ស៊ី នៅសាំងពេទ័របួគ៌។ នៅថ្ងៃទី១០ កក្កដា ឆ្នាំ១៧២៦ នីកូឡាបានស្លាប់ដោយសាររលាកខ្នែងពោះវៀន បន្ទាប់ពីរស់នៅនៅរុស្ស៊ីបានមួយឆ្នាំមក។ នៅពេលដែលដានីញែលទទួលតំណែងរបស់បងប្រុសគាត់នៅដេប៉ាតឺម៉ង់គណិតវិទ្យានិងរូបវិទ្យា គាត់បានស្នើឡើងថា តំណែងសរីរសាស្ត្រដែលគាត់បានបោះបង់គួរតែផ្ដល់ទៅមិត្តរបស់គាត់គឺអយល័រ។ ក្នុងខែវិច្ឆិកា ១៧២៦ បានព្រមទទួលយកតំណែងនេះ ប៉ុន្តែបានពន្យារពេលធ្វើដំណើរទៅសាំងពេទ័របួគ៌ ដោយសារពេលនោះគាត់បានដាក់ពាក្យធ្វើជាសាស្ត្រាចារ្យនៅសកលវិទ្យាល័យបាហ្សល។ ^[៩]

អយល័របានមករាជធានីរុស្ស៊ីនៅថ្ងៃ ១៧ ឧសភា ១៧២៧។ គាត់ត្រូវបានដំឡើងពីតំណែងដំបូងក្នុងដេប៉ាតឺម៉ង់វេជ្ជាសាស្ត្រទៅកាន់តំណែងថ្មីនៅដេប៉ាតឺម៉ង់គណិវិទ្យា។ គាត់ស្នាក់នៅជាមួយដានីញែលប៊ែរនូលី ដែលគាត់តែងធ្វើការជាមួយគ្នាយ៉ាងស្និទ្ធស្នាល។ អយល័ររៀនភាសារុស្ស៊ីបានស្ទាត់ជំនាញប្រើការបាន ហើយចាប់ផ្ដើមជីវិតនៅសាំងពេទ័របួគ៌។ គាត់ក៏បានធ្វើការងារបន្ថែមជាពេទ្យទាហាននៅកងនាវារបស់រុស្ស៊ីផងដែរ។ ^[១០]

បណ្ឌិត្យសភានៅសាំងពេទ័របួគ៌ បានបង្កើតឡើងដោយមហារាជភេទ័រ ដែលទ្រង់មានគោលបំណងអភិវឌ្ឍវិស័យអប់រំរបស់រុស្ស៊ី និងកាត់បន្ថយគម្លាតផ្នែកវិទ្យាសាស្ត្រជាមួយលោកខាងលិច។ ជាលទ្ធផល ប្រទេសរុស្ស៊ីបានក្លាយជាទីចំណាប់អារម្មណ៍អ្នកប្រាជ្ញបរទេសដូចជាអយល័រ។ បណ្ឌិត្យសភាមានថវិកាដ៏ច្រើនលើសលប់ និងបណ្ណាល័យដ៏ធំទូលំទូលាយដែលបង្កើតចេញពីបណ្ណាល័យផ្ទាល់ខ្លួនរបស់ព្រះចៅអធិរាជភេទ័រផ្ទាល់ និងរបស់ពួកអភិជន។ ចំនួនសិស្សដ៏តិចតួចបំផុតត្រូវបានគេជ្រើសរើសឱ្យទៅសិក្សានៅបណ្ឌិត្យសភានេះ ដើម្បីកាត់បន្ថយការងារបង្រៀន តែបង្កើនការងារស្រាវជ្រាវវិញ ដូច្នេះវាបានផ្ដល់ពេលវេលានិងសេរីភាពសម្រាប់ធ្វើការស្រាវជ្រាវផ្នែកវិទ្យាសាស្ត្រ។ ^[៨]

ឧបការីនីរបស់បណ្ឌិត្យសភា កាតេរីនទី១ (Catherine) បានអនុវត្តបន្តគោលនយោបាយរបស់ស្វាមីនាង បានស្លាប់មុនពេលដែលអយល័រមកដល់។ ពួកអភិជនរបស់រុស្ស៊ីបានបង្កើនឥទ្ធិពលរបស់ខ្លួនក្នុងរាជ្យរបស់ភេទ័រទី២ ដែលទើបតែមានអាយុ១២ឆ្នាំ។ ពួកអភិជនបានសង្ស័យពីពួកសមាជិកបណ្ឌិតសភាដែលជាជនបរទេស ហើយក៏កាត់ផ្ដាច់ការផ្ទត់ផ្គង់ហិរញ្ញវត្ថុ និងបង្កជាការលំបាកផ្សេងៗដល់អយល័រនិងសហការីរបស់គាត់។

ស្ថានភាពបានប្រសើរជាងមុនបន្តិចក្រោយពេលដែលភេទ័រទី២ បានស្លាប់ ហើយអយល័របានឡើងឋានៈយ៉ាងឆាប់រហ័សនៅក្នុងបណ្ឌិត្យសភា និងត្រូវបានតែងតាំងជាប្រូហ្វ៊េស្ស៊័ររូបវិទ្យានៅឆ្នាំ១៧៣១។ ពីរឆ្នាំក្រោយមក ដានីញែលប៊ែរនូលី ដែលបានធុញទ្រាន់នឹងភាពតឹងរ៉ឹងនិងភាពប្រទូសរ៉ាយដែលគាត់បានប្រឈមមុខនៅសាំងពេទ័របួគ៌ បានត្រលប់មកកាន់បាហ្សលវិញ។ អយល័របានបន្តតំណែងពីគាត់ ធ្វើជាប្រធានដេប៉ាតឺម៉ង់ផ្នែកគណិតវិទ្យា។ ^[១១]

នៅថ្ងៃទី៧ មករា ១៧៣៤ គាត់បានរៀបការជាមួយ Katharina Gsell (1707–1773), ដែលជាកូនស្រីរបស់ Georg Gsell, ដែលជាជាងគំនូរមកបណ្ឌិត្យសភា Gymnasium។^[១២] គ្រួសារថ្មីនេះបានទិញផ្ទះមួយជាប់ទន្លេនេវ៉ា (Neva)។ ក្នុងចំណោមកូនរបស់គាត់ទាំង១៣នាក់ មានតែ៥នាក់តែប៉ុណ្ណោះដែលអាចរស់ដល់ធំបាន។ ^[១៣]

ជីវិតនៅប៊ែរឡាំង

ដោយព្រួយបារម្ភពីសង្គ្រាមផ្ទៃក្នុងដែលចេះតែបន្តនៅរុស្ស៊ី អយល័របានចាកចេញពីសាំងពេទ័របួគ៌ នៅថ្ងៃទី១៩ មិថុនា ឆ្នាំ១៧៤១ ដើម្បីទៅទទួលតំណែងថ្មីនៅបណ្ឌិត្យសភាប៊ែរឡាំង ដែលត្រូវបានផ្ដល់ដោយព្រះចៅអធិរាជហ្វ្រេឌ្រិចរបស់រាជាណាចក្រប្រយសិន។ គាត់រស់នៅអស់រយៈពេល២៥ឆ្នាំនៅប៊ែរឡាំង ដែលនៅទីនោះគាត់សរសេរអត្ថបទផ្សាយបានចំនួន៣៨០អត្ថបទ។ នៅប៊ែរឡាំង គាត់បានបោះពុម្ពផ្សាយសៀវភៅពីរក្បាលដែលធ្វើឱ្យគាត់ល្បីបំផុត៖ Introductio in analysin infinitorum, សៀវភៅសរសេរពីអនុគមន៍ដែលបានបោះពុម្ពផ្សាយនៅឆ្នាំ១៧៤៨ និង Institutiones calculi differentialis,^[១៤] ដែលបានបោះពុម្ពផ្សាយនៅឆ្នាំ 1755 ក្រោមប្រធានបទគណនាឌីផេរ៉ង់ស្យែល។^[១៥] ក្នុងឆ្នាំ១៧៥៥ គាត់ត្រូវបានគេបោះឆ្នោតតែងតាំងជាសមាជិកបរទេសនៃបណ្ឌិត្យសភាវិទ្យាសាស្ត្រស៊ុយអ៊ែដ។

អយល័រត្រូវស្នើឱ្យធ្វើជាគ្រូរបស់ព្រះអង្គម្ចាស់ក្សត្រីនៃ Anhalt-Dessau, ដែលត្រូវជាក្មួយរបស់ហ្វ្រេឌ្រិច។ អយល័របានសរសេរសំបុត្រជាង២០០ទៅកាន់នាង, ដែលសំបុត្រទាំងនោះក្រោយមកត្រូវបានគេចងក្រងជាសៀវភៅដែលលក់ដាច់បំផុត ដែលមានចំណងជើងថា សំបុត្ររបស់អយល័រលើមុខវិជ្ជាផ្សេងៗក្នុងទស្សនវិជ្ជាធម្មជាតិទៅកាន់ព្រះអង្គម្ចាស់ក្សត្រីរបស់អាល្លឺម៉ង់ (Letters of Euler on different Subjects in Natural Philosophy Addressed to a German Princess)។ សៀវភៅនេះនិយាយពីការពន្យល់បកស្រាយលើមុខវិជ្ជាផ្សេងៗ ដែលជាប់ទាក់ទងនឹងរូបវិទ្យានិងគណិតវិទ្យា ក៏ដូចជាផ្ដល់នូវការយល់ដឹងយ៉ាងស៊ីជម្រៅទៅលើបុគ្គលភាពរបស់អយល័រនិងជំនឿរបស់គាត់លើសាសនា។ សៀវភៅនេះក្លាយជាសៀវភៅដែលគេអានច្រើនបំផុត ច្រើនជាងសៀវភៅផ្សេងទៀតរបស់គាត់ទៅទៀត។ សៀវភៅនេះត្រូវបានបោះពុម្ពផ្សាយពាសពេញអឺរ៉ុបនិងសហរដ្ឋអាមេរិច។ ប្រជាប្រិយភាពរបស់ 'សំបុត្រ' ទាំងនេះ បង្ហាញពីសមត្ថភាពរបស់អយល័រក្នុងទាក់ទងផ្នែកវិទ្យាសាស្ត្រយ៉ាងមានប្រសិទ្ធភាពជាមួយអ្នកស្ដាប់ធម្មតា ដែលជាសមត្ថភាពពិសេសដ៏កម្រមួយសម្រាប់អ្នកវិទ្យាសាស្ត្រ។ ^[១៥]

ទោះបីជាអយល័របានផ្ដល់វិភាគទានយ៉ាងសម្បើមដល់កិត្តិយសរបស់បណ្ឌិត្យសភាអាល្លឺម៉ង់យ៉ាងនេះក្ដី ក៏គាត់ត្រូវគេបង្ខំឱ្យចាកចេញពីប៊ែរឡាំងដែរ។ រឿងនេះមូលហេតុម្យ៉ាង ដោយសារអយល័រមិនសូវត្រូវគ្នាជាមួយហ្វ្រេឌ្រិចផង ដែលចាត់បានចាត់ទុកថាអយល័រមិនសូវឆ្លាត, ជាពិសេសបើធៀបនឹងរង្វង់អ្នកទស្សនវិទូដែលស្តេចអាល្លឺម៉ង់បាននាំយកមកបណ្ឌិត្យសភា។ វ៉ុលទែរជាមនុស្សម្នាក់ក្នុងចំណោមទស្សនវិទូរបស់ហ្វ្រេឌ្រិចជួលមក ហើយវ៉ុលទែរទទួលបាននូវតំណែងរបស់ខ្ពង់ខ្ពស់មួយនៅក្នុងរង្វង់សង្គមស្ដេច។ អយល័រ មនុស្សកាន់ធម៌អាថ៌ធម្មតា និងជាអ្នកធ្វើការធ្ងន់ ក្លាយជាវត្ថុសាមញ្ញក្នុងជំនឿនិងរសជាតិរបស់ស្ដេច។ អយល័របានប្រឆាំងនឹងវ៉ុលទែរក្នុងផ្លូវច្រើនយ៉ាង។ អយល័រខ្សោយខាងភាសាការទូត ហើយចង់តែប្រកែកគ្នាពីប្រធានបទដែលគាត់ដឹងតិចតួច បានក្លាយជាផ្ទាំងស៊ីបរបស់វ៉ុលទែរ។ ^[១៥] ហ្វ្រេឌ្រិចបានសម្ដែងនូវការខកចិត្តចំពោះសមត្ថភាពវិស្វកម្មរបស់អយល័រថា ៖

“

យើងចង់បាញ់ទឹកស្រោចផ្កា៖ អយល័រគាត់គណនាកម្លាំងរបស់កង់បង្វឹលចាំបាច់ដើម្បីអូសទឹកឡើងដល់អាងស្តុក ដែលទឹកត្រូវបង្ហួរតាមទុយ៉ួចេញពីអាងនោះមកវិញ ហើយចុងក្រោយឱ្យទឹកបាញ់ចេញមកនៅSanssouci។ រហាត់របស់យើងធ្វើមកត្រឹមត្រូវតាមធរណីមាត្រល្អណាស់ ហើយថាវាមិនអាចអូសទឹកម៉ាផ្តិលទៅដាក់នៅក្នុងអាងចម្ងាយតែ៥០ជំហាន។ គ្មានបានការលើសពីគ្មានបានការទៅទៀត! ធរណីមាត្រគ្មានបានការ!^[១៦]

”

ពិការភាពភ្នែក

ភ្នែករបស់អយល័របានខូចខាតយ៉ាងខ្លាំងក្នុងអំលុងអាជីពជាគណិតវិទូរបស់គាត់។ បីឆ្នាំបន្ទាប់គាត់ធ្លាក់ខ្លួនឈឺស្ទើរស្លាប់នៅឆ្នាំ១៧៣៥ ភ្នែកខាងស្ដាំរបស់គាត់ស្ទើរតែខ្វាក់ ប៉ុន្តែគាត់បានបន្ទោសបញ្ហានេះថាមកការលំបាកក្នុងការធ្វើផែនទីនៅបណ្ឌិតសភាសាំងពេទ័របួក៌ទៅវិញ។ ភ្នែកខាងស្ដាំរបស់គាត់នេះ បានខូចកាន់ធ្ងន់ធ្ងរទៅៗ នៅពេលគាត់ស្នាក់នៅប៊ែរឡាំង រហូតដល់ហ្វ្រេឌ្រិចបានហៅគាត់សាក្លប (Cyclop)(មានន័យថា អាយក្សភ្នែកមួយ)។ ក្រោយមកទៀត អយល័របានកើតជំងឺភ្នែកឡើងបាយនៅភ្នែកខាងឆ្វេងដែលនៅល្អរបស់គាត់ ដែលជំងឺនេះធ្វើឱ្យគាត់ស្ទើរតែក្លាយជាមនុស្សខ្វាក់ទាំងស្រុងទៅហើយ នៅប៉ុន្មានសប្ដាហ៍ក្រោយពីជំងឺនេះត្រូវបានគេរកឃើញនៅឆ្នាំ១៧៦៦។ បើទោះជាយ៉ាងនេះក្ដី ស្ថានភាពរបស់គាត់មិនមានឥទ្ធិពលអ្វីខ្លាំងក្លាដល់ទិន្នផលការងាររបស់គាត់ឡើយ ព្រោះគាត់មានសមត្ថភាពគណនាមាត់ទទេពូកែ និងពូកែចងចាំរូបភាព។ ឧទាហរណ៍ អយល័រអាចសូត្រកំណាព្យរបស់ Aenid របស់ Virgil បានពីដើមដល់ចប់ដោយគ្មានទាក់ ហើយគ្រប់ទំព័រទាំងអស់នៃសៀវភៅនេះ គាត់អាចប្រាប់បានថាបន្ទាត់ណានៅខាងមុខ បន្ទាត់ណានៅខាងក្រោយបាន។ ដោយមានជំនួយពីស្មេររបស់គាត់ ស្នាដៃរបស់អយល័រនៅលើវិស័យផ្សេងៗតាមពិតបានកើនឡើងទៅវិញទេ។ គាត់សរសេរបានជាមធ្យមនូវភេភ័រគណិតវិទ្យាមួយជារៀងរាល់សប្ដាហ៍ក្នុងឆ្នាំ១៧៧៥។^[៣]

ការត្រលប់ទៅកាន់រុស្ស៊ីវិញ

ស្ថានភាពនៅរុស្ស៊ីបានប្រសើរឡើងវិញបន្ទាប់ពីការឡើងគ្រងរាជ្យរបស់មហារាជCatherine ហើយនៅឆ្នាំ១៧៦៦ អយល័របានយល់ព្រមតាមការអញ្ជើញត្រលប់ទៅបណ្ឌិត្យសភាសាំងពេទ័របួគ៌វិញ ហើយបានរស់នៅរុស្ស៊ីរហូតដល់ជីវិតចុងក្រោយ។ ការស្នាក់នៅលើកទី២របស់គាត់នៅរុស្ស៊ីនេះ គាត់ជួបប្រទះនូវគ្រោះអាក្រក់ដ៏គួរឱ្យរន្ធត់។ អគ្គិភ័យនៅសាំងពេទ័របួគ៌ក្នុងឆ្នាំ១៧៧១ បានបំផ្លាញផ្ទះរបស់គាត់ និងស្ទើរតែបំផ្លាញជីវិតរបស់គាត់ផងដែរ។ ក្នុងឆ្នាំ១៧៧៣ គាត់បានបាត់បង់ Katharina ប្រពន្ធរបស់គាត់ក្នុងអាយុ៤០ឆ្នាំ។ ៣ឆ្នាំក្រោយមក គាត់បានរៀបការជាមួយប្អូនស្រីចុងរបស់ប្រពន្ធដើមគាត់គឺ Salome Abigail Gsell (1723–1794).^[១៨] អាពាហ៍ពិពាហ៍បានឋិតឋេររហូតដល់ថ្ងៃគាត់ស្លាប់។

នៅថ្ងៃ ១៨ កញ្ញា ១៧៨៣ បន្ទាប់ពីទទួលទានអាហារថ្ងៃត្រង់ជាមួយគ្រួសាររបស់គាត់ ក្នុងពេលសន្ទនាជាមួយAnders Lexell អំពីរបកគំហើញថ្មីនៃទ្វីបអ៊ុយរ៉ានុសនិងគន្លងរបស់វា, អយល័របានកើតជំងឺដាច់សរសៃឈាមក្នុងខួរក្បាល ហើយបានស្លាប់ប៉ុន្មានម៉ោងក្រោយមក។ ^[១៩] ដំណឹងមរណភាពខ្លីមួយសម្រាប់បណ្ឌិតសភារុស្ស៊ី ត្រូវបានសរសេរដោយJacob von Shtelin និងពាក្យសរសើរដ៏ក្បោះក្បាយមួយ^[២០] ត្រូវបានសរសេរនិងអានក្នុងពិធីរំលឹកវិញ្ញាណក្ខន្ធដោយគណិវិទួរុស្ស៊ី Nicolas Fuss, ដែលជាសាវ័កមួយរបស់អយល័រ។ ក្នុងពាក្យសរសើរសម្រាប់បណ្ឌិត្យសភាបារាំង ដែលសរសេរដោយគណិតវិទូនិងទស្សនវិទូបារាំងMarquis de Condorcet, គាត់បានសរសេរថា

“

…il cessa de calculer et de vivre — … គាត់នៅតែបន្តការគណនា ហើយរស់នៅជារៀងរហូត^[២១]

”

គាត់ត្រូវបានគេបញ្ចុះនៅជាប់ផ្នូររបស់ Katharina នៅវិមានសព Smolensk Lutheran នៅកោះ Vasilievsky។ ក្នុងឆ្នាំ១៧៨៥ បណ្ឌិត្យសភាវិទ្យាសាស្ត្របានដាក់តាំងរូបសំណាកលេអុនហាដអយល័រនៅជាប់នឹងកៅអីរបស់ប្រធានបណ្ឌិត្យសភា។ ក្នុងឆ្នាំ១៨៣៧ បណ្ឌិត្យសភាវិទ្យាសាស្ត្របានដាក់ប្លាកមុខផ្នូររបស់គាត់ ហើយនៅឆ្នាំ១៩៥៦ ដែលត្រូវជាខួបកំណើតទី២៥០របស់អយល័រ ផ្នូររបស់គាត់ត្រូវបានគេប្ដូរទៅដាក់នៅវិមានសពសតវត្សរ៍ទី១៨ នៅ Alexander Nevsky Lavraវិញ។ ^[២២]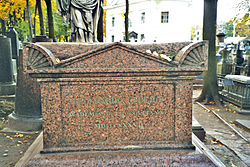

វិភាគទានក្នុងវិស័យគណិតវិទ្យានិងរូបវិទ្យា

ស្នាដៃរបស់អយល័រមាននៅក្នុងស្ទើរគ្រប់វិស័យនៃគណិតវិទ្យា៖ ធរណីមាត្រ គណនាមិនកំណត់ ត្រីកោណមាត្រ ពីជគណិត និងទ្រឹស្ដីនព្វន្ត ព្រមទាំងរូបវិទ្យានៃមជ្ឈដ្ឋានជាប់ ទ្រឹស្ដីព្រះចន្ទនិងផ្នែកផ្សេងទៀតនៃរូបវិទ្យា។

និមិត្តសញ្ញាគណិតវិទ្យា

អយល័របានបង្កើតនិងធ្វើឱ្យនិមិត្តសញ្ញាមួយចំនួនពេញនិយមប្រើតាមរយៈសៀវភៅជាច្រើនរបស់គាត់ដែលបានផ្សព្វផ្សាយយ៉ាងទូលំទូលាយ។ គួរឱ្យកត់សម្គាល់ជាងគេ គឺគាត់ជាអ្នកបង្កើតសញ្ញាអនុគមន៍ ដែលសរសេរក្រោមរាងជា $\ f(x)$ តំណាងឱ្យអនុគមន៍ $\ f$ អនុវត្តលើអថេរ $\ x$ ។ គាត់ជាអ្នកបង្កើត ពាក្យតំណាងអនុគមន៍ត្រីកោណមាត្រ, ប្រើ $\ e$ តាងគោលលោការីតធម្មជាតិ (ដែលជួនកាលគេហៅថាចំនួនអយល័រ), ប្រើអក្សរក្រិចស៊ិចម៉ា $\ \Sigma$ តាងឱ្យផលបូក និង អក្សរ $\ i$ តាងឱ្យឯកតាប្រឌិតក្នុងចំនួនកុំផ្លិច។^[២៣] ការប្រើអក្សរ $\ \pi$ តាងឱ្យផលធៀបបរិមាត្ររង្វង់ធៀបនឹងអង្កត់ផ្ចិតរង្វង់ ក៏អយល័រជាអ្នកនាំឱ្យមានការពេញនិយមប្រើដែរ, តែនិមិត្តសញ្ញានេះមិនមែនគាត់ជាបង្កើតឱ្យប្រើមុនគេឡើយ។^[២៤]

វិភាគ

ការអភិវឌ្ឍនៃការគណនាមិនកំណត់កំពុងតែឋិតនៅក្នុងដំណាក់កាលពុះកញ្ជ្រោលក្នុងវិស័យស្រាវជ្រាវផ្នែកគណិតវិទ្យានាសតវត្សរ៍ទី១៨ ហើយត្រកូលប៊ែរនូលី ដែលជាមិត្តភក្តិរបស់អយល័រ ជាអ្នកមានចំណែកដ៏ធំបំផុតក្នុងការធ្វើឱ្យវិស័យនេះរីកចម្រើនបំផុត។ ដោយសារឥទ្ធិពលរបស់ត្រកូលនេះ ការស្រាវជ្រាវផ្នែកគណិតគណនាបានក្លាយជាប្រធានបទចម្បងសម្រាប់អយល័រ។ បើទោះបីជាសម្រាយបញ្ជាក់ខ្លះរបស់អយល័រ មិនត្រូវបានទទួលស្គាល់ដោយវិធីគណិតទំនើបស្មុគស្មាញក៏ដោយ^[២៥] ក៏គំនិតរបស់អយល័របានជួយធ្វើឱ្យមានការរីកចម្រើនដល់ផ្នែកនេះជាខ្លាំង។ ភាពល្បីល្បាញរបស់អយល័រនៅក្នុងគណិតវិភាគគឺការបានប្រើយ៉ាងញឹកញាប់និងបានអភិវឌ្ឍស៊េរីស្វ័យគុណគឺការបំបែកអនុគមន៍មួយជាតួជាច្រើនមិនកំណត់បូកចូលគ្នា ដូចជា

e^{x}=\sum _{n=0}^{\infty }{x^{n} \over n!}=\lim _{n\to \infty }\left({\frac {1}{0!}}+{\frac {x}{1!}}+{\frac {x^{2}}{2!}}+\cdots +{\frac {x^{n}}{n!}}\right).

ជាពិសេសនោះ អយល័របានស្រាយបញ្ជាក់តាមវិធីផ្ទាល់នូវការបំបែកជាស៊េរីស្វ័យគុណនៃ e និងអនុគមន៍តង់សង់ច្រាស។ (ការស្រាយបញ្ជាក់តាមវិធីមិនផ្ទាល់តាមរយៈវិធីស៊េរីស្វ័យគុណច្រាស ត្រូវបានធ្វើឡើងជាដំបូងដោយញូតុននិងឡាយប៍នីត(Leibniz) ក្នុងរវាងឆ្នាំ១៦៧០ និង ១៦៨០។) គាត់បានប្រើស៊េរីស្វ័យគុណដើម្បីដោះស្រាយចំណោទបាហ្សល (Bazel) ដ៏ល្បីល្បាញក្នុងឆ្នាំ១៧៣៥ (ហើយគាត់បានផ្ដល់អំណះអំណាងបន្ថែមកាន់តែច្បាស់លាស់ជាងមុននៅឆ្នាំ១៧៤១):^[២៥]

\sum _{n=1}^{\infty }{1 \over n^{2}}=\lim _{n\to \infty }\left({\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots +{\frac {1}{n^{2}}}\right)={\frac {\pi ^{2}}{6}}.

អយល័របានណែនាំការប្រើប្រាស់អនុគមន៍អ៊ិចស្ប៉ូណង់ស្យែល និងលោការីតនៅក្នុងបំណកស្រាយបែបវិភាគ។ គាត់បានរកឃើញវិធីសរសេរអនុគមន៍លោការីតដោយប្រើស៊េរីស្វ័យគុណ ហើយគាត់បានកំណត់ប្រកបដោយជោគជ័យនូវលោការីតនៃចំនួនអវិជ្ជមាននិងកុំផ្លិច ដូច្នេះហើយបានពង្រីកដែនកំណត់ប្រើប្រាស់នៃលោការីតក្នុងគណិតវិទ្យា។^[២៣] គាត់ក៏បានកំណត់នូវអនុគមន៍អ៊ិចស្ប៉ូណង់ស្យែលសម្រាប់ចំនួនកុំផ្លិចផងដែរ និងបានរកឃើញទំនាក់ទំនងនៃអនុគមន៍អ៊ិចស្ប៉ូណង់ស្យែលជាមួយនឹងអនុគមន៍ត្រីកោណមាត្រ។ សម្រាប់ចំនួនពិតφមួយ រូបមន្តអយល័រចែងថា អនុគមន៍អ៊ិចស្ប៉ូណង់ស្យែលកុំផ្លិចផ្ទៀងផ្ទាត់

e^{i\varphi }=\cos \varphi +i\sin \varphi .\,

ករណីពិសេសនៃរូបមន្តខាងលើត្រូវបានគេស្គាល់ថាជាឯកលក្ខណភាពអយល័រ

e^{i\pi }+1=0\,

ដែលលោករីឆាតហ្វេយម៉ាន(Richard Feynman) បានហៅថារូបមន្តដ៏ពិសេសបំផុតក្នុងគណិតវិទ្យា ព្រោះក្នុងរូបមន្តនេះគេប្រើតែសញ្ញាបូក សញ្ញាគុណ អ៊ិចស្ប៉ូណង់ស្យែល និងសមភាពតែម្ដងគត់ ហើយប្រើតែម្ដងគត់នូវមេគុណ 0, 1, e, i និង n ។^[២៦] ក្នុងឆ្នាំ១៩៨៨ អ្នកអានរបស់ ទស្សនាវដ្ដី Mathematical Intelligencer បានបោះឆ្នោតរូបមន្តជារូបមន្តគណិតវិទ្យាស្អាតបំផុតជានិរន្តរ៍។ ^[២៧] ជាសរុប អយល័រជាម្ចាស់នៃរូបមន្តចំនួនបីក្នុងចំណោមរូបមន្តគណិតវិទ្យាទាំងប្រាំលើគេនៅក្នុងការបោះឆ្នោតនោះ។ ^[២៧]

រូបមន្តដឺម័រ ជាវិបាកផ្ទាល់នៃ រូបមន្តអយល័រ។

ជាបន្ថែម អយល័របានបង្កើតទ្រឹស្ដី អនុគមន៍មិនពីជគណិត (transcendental function) លំដាប់ខ្ពស់ ដោយបង្កើតអនុគមន៍ហ្កាម៉ា និងបានបង្កើតវិធីថ្មីដើម្បីដោះស្រាយសមីការដឺក្រេទីបួន។ គាត់ក៏បានរកឃើញវិធីដើម្បីគណនាអាំងតេក្រាលមានលីមីតកុំផ្លិចផងដែរ ដែលបានជំនួយដល់ការអភិវឌ្ឍនៃការវិភាគកុំផ្លិចទំនើប និងបានបង្កើតគណិតគណនានៃអថេរ ក្នុងនោះមានសមីការអយល័រ-ឡាក្រង់ដ៏ល្បីល្បាញ។

អយល័រក៏ជាអ្នកផ្ដើមគំនិតប្រើប្រាស់វិធីវិភាគដើម្បីដោះស្រាយចំណោទទ្រឹស្ដីនព្វន្តផងដែរ។ ក្នុងការងារនោះ គាត់បានបង្រួបបង្រួមមែកធាងគណិតពីរដែលបែកពីគ្នា ហើយបានបង្កើតវិស័យស្រាវជ្រាវថ្មីមួយគឺ ទ្រឹស្ដីនព្វន្តវិភាគ។ ក្នុងវិស័យថ្មីនៃគណិតវិទ្យានេះ អយល័របានបង្កើតទ្រឹស្ដីនៃស៊េរីអ៊ីពែរធរណីមាត្រ, ស៊េរី-q, អនុគមន៍ត្រីកោណមាត្រអ៊ីពែរបូលិច និងទ្រឹស្ដីវិភាគនៃប្រភាគជាប់ទូទៅ។ ឧទាហរណ៍ គាត់បានស្រាយបញ្ជាក់ពីភាពមិនកំណត់នៃចំនួនបឋម ដោយប្រើភាពរីកនៃ ស៊េរីអាម៉ូនិច ហើយគាត់បានប្រើប្រាស់វិធីវិភាគដើម្បីស្វែងយល់ពីរបាយនៃចំនួនបឋម។ ស្នាដៃអយល័រក្នុងវិស័យនេះបានធ្វើឱ្យរីកចម្រើនដល់ទ្រឹស្ដីបទនៃចំនួនបឋម។ ^[២៨]

ទ្រឹស្ដីនព្វន្ត

ចំណាប់អារម្មណ៍របស់អយល័រលើទ្រឹស្តីនៃចំនួនអាចបណ្ដាលមកពីឥទ្ធិពលរបស់ Christian Goldbach ដែលជាមិត្តភក្ដិនៅបណ្ឌិត្យសភាសាំងភីធ័រស្ប៊័ក៌។ ការងារដំបូងៗភាគច្រើនរបស់អយល័រលើទ្រឹស្ដីនព្វន្ត មានគោលការណ៍ផ្អែកលើទ្រឹស្តីនានារបស់ព្យែរដឺភែម៉ា។ អយល័របានអភិវឌ្ឍគំនិតខ្លះរបស់ភែម៉ា ហើយបានបកស្រាយរកកំហុសក្នុងការទស្សន៍ទាយ(conjecture) ខ្លះៗរបស់ភែម៉ា។

អយល័របានភ្ជាប់លក្ខណៈនៃរបាយចំនួនបឋមទៅនឹងគណិតវិភាគ។ គាត់បានបង្ហាញថា ផលបូកនៃចម្រាសរបស់ចំនួនបឋមជាស៊េរីរីក។ ក្នុងការបកស្រាយនោះ គាត់បានរកឃើញពីការទាក់ទងគ្នារវាងអនុគមន៍ហ្សែតារីម៉ាន់ និងចំនួនបឋម, ទំនាក់ទំនងនេះគេបានដាក់ឈ្មោះថារូបមន្តផលគុណអយល័រសម្រាប់អនុគមន៍ហ្សែតារីម៉ាន់។

អយល័របានស្រាយបញ្ជាក់ឯកលក្ខណភាពញូតុន, កូនទ្រឹស្ដីបទភែម៉ា, ទ្រឹស្ដីបទភែម៉ានៃផលបូកចំនួនការេពីរ ហើយគាត់បានផ្ដល់វិភាគទានយ៉ាងសម្បើមដល់ទ្រឹស្ដីបទការេបួនរបស់ឡាក្រង់។ គាត់ក៏បានបង្កើតអនុគមន៍តូស្ហិន $\ \phi (n)$ ដែលស្មើនឹងចំនួននៃចំនួនគត់វិជ្ជមានដែលតូចជាងឬស្មើចំនួនគត់ $\ n$ ហើយដែលបឋមនឹង $\ n$ ។ ដោយប្រើលក្ខណៈនេះ គាត់បានធ្វើសាមញ្ញភាវូបនីយកម្មកូនទ្រឹស្តីបទភែម៉ា ឱ្យក្លាយជាទ្រឹស្ដីបទថ្មីដែលហៅថាទ្រឹស្ដីបទអយល័រ។ គាត់ក៏ផ្ដល់វិភាគទានយ៉ាងសម្បើមផងដែរដល់ទ្រឹស្ដីបទនៃសម្បុណ្ណលេខ (perfect number) ដែលទ្រឹស្ដីនៃចំនួននេះបានធ្វើឱ្យគណិតវិទូចាប់អារម្មណ៍ជាខ្លាំងតាំងពីសម័យអឺគ្លីដមក។ អយល័របានអភិវឌ្ឍទ្រឹស្ដីនៃចំនួនបឋម ហើយបានធ្វើការស្មានទុកនូវទ្រឹស្ដីនៃភាពច្រាសកាដ្រាទិច។ គោលការណ៍ទាំងពីរនេះត្រូវបានគេចាត់ទុកជាទ្រឹស្ដីបទគ្រឹះនៃទ្រឹស្ដីនព្វន្ត ហើយគំនិតរបស់អយល័របានបើកជាផ្លូវសម្រាប់ការងាររបស់ខាលហ្វ្រ៊ីឌ្រិចគ្ហោស។ ^[២៩]

នៅឆ្នាំ១៧៧២ អយល័របានបង្ហាញថា $\ 2^{31}-1=2'147'483'647$ ជាចំនួនបឋមមែរសែន។ ចំនួនបឋមនេះនៅតែជាចំនួនបឋមធំបំផុតដែលគេស្គាល់រហូតដល់ឆ្នាំ១៨៦៧។^[៣០]

ទ្រឹស្ដីបទក្រាប

ផែនទីក្រុងឃើនិច្សប៊ែក៌ នៅសម័យអយល័របង្ហាញពីតាំងរបស់ពិតប្រាកដរបស់ស្ពានទាំងប្រាំពីរ

ក្នុងឆ្នាំ១៧៣៦ អយល័របានដោះស្រាយចំណោទមួយដែលគេស្គាល់ថាស្ពានទាំងប្រាំពីរនៃឃើនិច្សប៊ែក៌។^[៣១] ក្រុងឃើនិច្សប៊ែក៌ នៃរាជាណាចក្រប្រយសិន បានតាំងនៅមាត់ទន្លព្រីគឹល ហើយមានកោះធំៗពីរ ដែលតភ្ជាប់គ្នានឹងដីគោកដោយស្ពានចំនួន៧។ ចំណោទនោះគឺថាតើគេអាចដើរកាត់ស្ពាននីមួយៗគ្រប់ស្ពាន និងតែម្ដងគត់ ហើយដើរមកដល់កន្លែងដើមវិញបានដែរឬទេ?។ អយល័របានរកឃើញថា គេមិនអាចធ្វើដូច្នេះបានទេ៖ ក្នុងករណីនេះ គេមិនអាចរកបាននូវ សៀគ្វីអយល័របានឡើយ។ ដំណោះស្រាយនេះត្រូវបានគេចាត់ទុកថាជាទ្រឹស្ដីក្រាបដំបូងគេ ហើយជាពិសេសជាទ្រឹស្ដីទីមួយនៃទ្រឹស្ដីក្រាបប្លង់ ។^[៣១]

អយល័របានរកឃើញរូបមន្ត៖ $\ V-E+F=2$ ដែលភ្ជាប់ទំនាក់ទំនងចំនួនកំពូល, ជ្រុង និងមុខរបស់ពហុមុខប៉ោង,^[៣២] ហើយរូបមន្តនេះកែសម្រួលមកសម្រាប់ប្រើក្នុងក្រាបប្លង់បានដែរ។ ចំនួនថេរនៅក្នុងរូបមន្តនេះត្រូវបានគេស្គាល់ថាជាលក្ខណៈអយល័រសម្រាប់ក្រាប(ឬវត្ថុគណិតផ្សេងទៀត), ហើយជាប់ទាក់ទងទៅនឹងgenus នៃវត្ថុ។^[៣៣] ការសិក្សានិងការធ្វើឱ្យរូបមន្តនេះកាន់តែទូលំទូលាយជាងមុន ជាពិសេសដោយលោក Cauchy^[៣៤] និង L'Huillier,^[៣៥] គឺជាប្រភពនៃតូប៉ូឡូស៊ី។

គណិតវិទ្យាអនុវត្តន៍

ជោគជ័យដ៏សម្បើមបំផុតខ្លះរបស់អយល័រគឺភាពជោគជ័យក្នុងការដោះស្រាយបញ្ហាក្នុងពិភពលោកជាក់ស្ដែងតាមវិភាគ និងការអធិប្បាយទៅលើការអនុវត្តជាលេខនៃចំនួន Bernoulli, ស៊េរី Fourier, ដ្យាក្រាមវ៉ែន (Venn), ចំនួនអយល័រ, ថេរ $\ e$ , ប្រភាគជាប់ និងអាំងតេក្រាល។ គាត់បានធ្វើអាំងតេក្រាលសមីការឌីផេរ៉ង់ស្យែល Leibniz ដោយប្រើវិធីភ្លុចស្យុងរបស់ញូតុន និងបានបង្កើតវិធីងាយស្រួលប្រើដែលគេអាចយកទៅប្រើក្នុងការដោះស្រាយបញ្ហារូបវិទ្យា។ គាត់បានធ្វើឱ្យរីកចម្រើនផ្នែកគណនាតម្លៃប្រហែលនៃអាំងតេក្រាល ដោយបង្កើតវិធីប្រហែលដែលគេស្គាល់សព្វថ្ងៃនេះថាជាវិធីតម្លៃប្រហែលអយល័រ។ វិធីតម្លៃប្រហែលដែលល្បីបំផុតគឺ វិធីអយល័រ និង រូបមន្តអយល័រ-ម៉ាក់ឡូរ៉ាំង។ គាត់បានជួយសម្រួលដល់ការប្រើប្រាស់សមីការឌីផេរ៉ង់ស្យែល ជាពិសេសបានបង្កើត ថេរអយល័រ-ម៉ាសឈែរ៉ូនី ៖

 $\gamma =\lim _{n\rightarrow \infty }\left(1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots +{\frac {1}{n}}-\ln(n)\right).$

ការបង្កើតដ៏ចម្លែកមួយរបស់អយល័រគឺអនុវត្តគណិតវិទ្យាក្នុងតន្ត្រី។ ក្នុងឆ្នាំ១៧៣៩ គាត់បានសរសេរ Tentamen novae theoriae musicae, ដោយសង្ឃឹមថានឹងអាចបញ្ចូលទ្រឹស្តីតន្ត្រីទៅក្នុងផ្នែកមួយនៃគណិតវិទ្យា។ ការងាររបស់គាត់មួយនេះមិនបានទទួលនូវការចាប់អារម្មណ៍ឱ្យបានទូលំទូលាយនោះទេ ហើយត្រូវបានគេចាត់ទុកថាគណិតវិទ្យាពេកសម្រាប់តន្ត្រីករ និងពោរពេញដោយតន្ត្រីពេកសម្រាប់គណិតវិទូ។^[៣៦]

រូបវិទ្យានិងតារាវិទ្យា

អយល័របានជួយអភិវឌ្ឍសមីការធ្នឹមអយល័រ–ប៊ែរនូលី, ដែលបានក្លាយជារបកគំហើញដ៏សម្បើមមួយស្រាប់វិស័យវិស្វកម្ម។ ក្រៅពីបានអនុវត្តឧបករណ៍វិភាគរបស់គាត់ប្រកបដោយជោគជ័យក្នុង មេកានិចក្លាស្ស៊ិច, អយល័របានអនុវត្តតិចនិចទាំងនេះទៅក្នុងបញ្ហាតារាវិទ្យាថែមទៀត។ ការងាររបស់គាត់លើផ្នែកតារាវិទូត្រូវបានទទួលស្គាល់ស្វាគមន៍ដោយរង្វាន់ដ៏ច្រើនផ្សេងគ្នាពីបណ្ឌិត្យសភាក្រុងប៉ារីស។ ស្នាដៃរបស់គាត់រួមមានការកំណត់ប្រកបសុក្រឹតភាពខ្ពស់បំផុតនូវគន្លងរបស់ផ្កាយដុះកន្ទុយនិងភពផ្សេងទៀត, ការយល់ដឹងពីលក្ខណៈនៃផ្កាយដុះកន្ទុយ, និងគណនាប៉ារ៉ាឡ័ក្ស របស់ព្រះអាទិត្យ។ ការគណនារបស់គាត់ក៏បានជួយដល់ការបង្កើត តារាងរយៈបណ្ដោយដែលសុក្រឹតជាងមុនផងដែរ។^[៣៧]

ជាងនេះទៅទៀត អយល័របានផ្ដល់វិភាគទានយ៉ាងសំខាន់ក្នុងវិស័យ អុបទិច។ គាត់បានបដិសេធទ្រឹស្ដីអង្គតូចនៃពន្លឺរបស់ញូតុន ក្នុងស្នាដៃ Opticks ដែលទ្រឹស្ដីនោះត្រូវបានគេទទួលស្គាល់យ៉ាងទូលំទូលាយជាយូរមកហើយ។ ភែបភ័រឆ្នាំ១៧៤០របស់គាត់ស្ដីពីអុបទិចបានបញ្ជាក់យ៉ាងច្បាស់ថា ទ្រឹស្ដីរលកនៃពន្លឺរបស់Christian Huygens នឹងក្លាយទស្សនៈថ្មីដែលគេទទួលស្គាល់ជាទូទៅទៅថ្ងៃមុខ ហើយទ្រឹស្តីនេះត្រូវបានគេទទួលស្គាល់ជាទូទៅរហូតមកដល់សម័យបង្កើតទ្រឹស្ដីបទកង់តូមនៃពន្លឺ។^[៣៨]

តក្កវិទ្យា

គាត់ក៏ត្រូវបានគេទទួលស្គាល់ផងដែរថាបានប្រើប្រាស់ខ្សែកោងបិទជិត ដើម្បីបកស្រាយអំណះអំណាងតក្កវិទ្យាបែបស៊ីឡូស៊ីក។ ដ្យាក្រាមទាំងនេះក្រោយមកត្រូវបានគេដាក់ឈ្មោះថា ដ្យាក្រាមអយល័រ។^[៣៩]

ឯកសារយោង

↑ The pronunciation /ˈjuːlər/ is incorrect. "Euler", Oxford English Dictionary, second edition, Oxford University Press, 1989 "Euler", Merriam–Webster's Online Dictionary, 2009. "Euler, Leonhard", The American Heritage Dictionary of the English Language, fourth edition, Houghton Mifflin Company, Boston, 2000. Peter M. Higgins (2007). Nets, Puzzles, and Postmen: An Exploration of Mathematical Connections. Oxford University Press. p. 43.
↑ Dunham, William (1999). Euler: The Master of Us All. The Mathematical Association of America. p. 17.
↑ ^៣,០ ^៣,១ Finkel, B.F. (1897). "Biography- Leonard Euler". The American Mathematical Monthly 4 (12). DOI:10.2307/2968971.
↑ Dunham, William (1999). Euler: The Master of Us All. The Mathematical Association of America. xiii. "Lisez Euler, lisez Euler, c'est notre maître à tous."
↑ Euler, Leonhard (1960). "Rettung der Göttlichen Offenbahrung Gegen die Einwürfe der Freygeister". Leonhardi Euleri Opera Omnia (series 3) 12.
↑ James, Ioan (2002). Remarkable Mathematicians: From Euler to von Neumann. Cambridge. p. 2. ល.ស.ប.អ. 0-521-52094-0.
↑ Translation of Euler's dissertation in English by Ian Bruce
↑ ^៨,០ ^៨,១ Calinger, Ronald (1996). "Leonhard Euler: The First St. Petersburg Years (1727–1741)". Historia Mathematica 23 (2). DOI:10.1006/hmat.1996.0015.
↑ Calinger, Ronald (1996). "Leonhard Euler: The First St. Petersburg Years (1727–1741)". Historia Mathematica 23 (2). DOI:10.1006/hmat.1996.0015.
↑ Calinger, Ronald (1996). "Leonhard Euler: The First St. Petersburg Years (1727–1741)". Historia Mathematica 23 (2). DOI:10.1006/hmat.1996.0015.
↑ Calinger, Ronald (1996). "Leonhard Euler: The First St. Petersburg Years (1727–1741)". Historia Mathematica 23 (2): 128–129. DOI:10.1006/hmat.1996.0015.
↑ Gekker, I.R.; Euler, A.A. (2007). "Leonhard Euler's family and descendants". ជា Bogoliubov, N.N.; Mikhaĭlov, G.K.; Yushkevich, A.P.. Euler and modern science. Mathematical Association of America. ល.ស.ប.អ. 088385564X. , p. 402.
↑ Fuss, Nicolas. "Eulogy of Euler by Fuss". Retrieved 30 August 2006.
↑ "E212 -- Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum". Dartmouth.
↑ ^១៥,០ ^១៥,១ ^១៥,២ Dunham, William (1999). Euler: The Master of Us All. The Mathematical Association of America. xxiv–xxv.
↑ Frederick II of Prussia (1927). Letters of Voltaire and Frederick the Great, Letter H 7434, 25 January 1778. Richard Aldington. New York: Brentano's.
↑ Calinger, Ronald (1996). "Leonhard Euler: The First St. Petersburg Years (1727–1741)". Historia Mathematica 23 (2): 154–155. DOI:10.1006/hmat.1996.0015.
↑ Gekker, I.R.; Euler, A.A. (2007). "Leonhard Euler's family and descendants". ជា Bogoliubov, N.N.; Mikhaĭlov, G.K.; Yushkevich, A.P.. Euler and modern science. Mathematical Association of America. ល.ស.ប.អ. 088385564X. , p. 405.
↑ A. Ya. Yakovlev (1983). Leonhard Euler. M.: Prosvesheniye.
↑ (1783). "Eloge de M. Leonhard Euler. Par M. Fuss.". Nova Acta Academia Scientarum Imperialis Petropolitanae 1: 159–212.
↑ Marquis de Condorcet. "Eulogy of Euler - Condorcet". Retrieved 30 August 2006.
↑ ទំព័រគំរូ:Findagrave
↑ ^២៣,០ ^២៣,១ Boyer, Carl B.; Uta C. Merzbach (1991). A History of Mathematics. John Wiley & Sons. pp. 439–445. ល.ស.ប.អ. 0-471-54397-7.
↑ Wolfram, Stephen. "Mathematical Notation: Past and Future". Retrieved August 2006. {{cite web}}: Check date values in: |accessdate= (help)
↑ ^២៥,០ ^២៥,១ Wanner, Gerhard; Harrier, Ernst (March 2005). Analysis by its history (1st រ.រ.). Springer. p. 62.
↑ Feynman, Richard (June 1970). "Chapter 22: Algebra". The Feynman Lectures on Physics: Volume I. p. 10.
↑ ^២៧,០ ^២៧,១ Wells, David (1990). "Are these the most beautiful?". Mathematical Intelligencer 12 (3): 37–41. DOI:10.1007/BF03024015.
Wells, David (1988). "Which is the most beautiful?". Mathematical Intelligencer 10 (4): 30–31. DOI:10.1007/BF03023741.
See also: Peterson, Ivars. "The Mathematical Tourist". Archived from the original on 2007-03-31. Retrieved March 2008. {{cite web}}: Check date values in: |accessdate= (help)
↑ Dunham, William (1999). "3,4". Euler: The Master of Us All. The Mathematical Association of America.
↑ Dunham, William (1999). "1,4". Euler: The Master of Us All. The Mathematical Association of America.
↑ Caldwell, Chris. The largest known prime by year
↑ ^៣១,០ ^៣១,១ Alexanderson, Gerald (July 2006). "Euler and Königsberg's bridges: a historical view". Bulletin of the American Mathematical Society 43. DOI:10.1090/S0273-0979-06-01130-X.
↑ Peter R. Cromwell (1997). Polyhedra. Cambridge: Cambridge University Press. pp. 189–190.
↑ Alan Gibbons (1985). Algorithmic Graph Theory. Cambridge: Cambridge University Press. p. 72.
↑ Cauchy, A.L. (1813). "Recherche sur les polyèdres—premier mémoire". Journal de l'Ecole Polytechnique 9 (Cahier 16): 66–86.
↑ L'Huillier, S.-A.-J. (1861). "Mémoire sur la polyèdrométrie". Annales de Mathématiques 3: 169–189.
↑ Calinger, Ronald (1996). "Leonhard Euler: The First St. Petersburg Years (1727–1741)". Historia Mathematica 23 (2): 144–145. DOI:10.1006/hmat.1996.0015.
↑ Youschkevitch, A P; Biography in Dictionary of Scientific Biography (New York 1970–1990).
↑ Home, R.W. (1988). "Leonhard Euler's 'Anti-Newtonian' Theory of Light". Annals of Science 45 (5): 521–533. DOI:10.1080/00033798800200371.
↑ Baron, M. E.; A Note on The Historical Development of Logic Diagrams. The Mathematical Gazette: The Journal of the Mathematical Association. Vol LIII, no. 383 May 1969.

តំណភ្ជាប់ខាងក្រៅ

ស្វែងយល់បន្ថែមអំពីលេអុនហាដ អយល័រលើ គម្រោងបងប្អូនរបស់វិគីភីឌា:
	សម្រង់ពាក្យសម្ដីពីវិគីសម្រង់ពាក្យ
	អត្ថបទប្រភពដើមពីវិគីប្រភព

LeonhardEuler.com
ទំព័រគំរូ:ScienceWorldBiography
Encyclopædia Britannica article
លេអុនហាដ អយល័រ at the Mathematics Genealogy Project.
How Euler did it contains columns explaining how Euler solved various problems
Euler Archive
Leonhard Euler – Œuvres complètes Gallica-Math
Euler Committee of the Swiss Academy of Sciences
References for Leonhard Euler
Euler Tercentenary 2007
The Euler Society
Euler Family Tree
Euler's Correspondence with Frederick the Great, King of Prussia
O'Connor, John J.; Robertson, Edmund F., "លេអុនហាដ អយល័រ", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Euler.html .
Euler Quartic Conjecture
Portrait of Leonhard Euler from the Lick Observatory Records Digital Archive, UC Santa Cruz Library's Digital Collections Archived 2017-03-13 at the វេយប៊ែខ ម៉ាស៊ីន.
Euler's (1769–1771) Dioptricae, 3 vols. Archived 2017-03-30 at the វេយប៊ែខ ម៉ាស៊ីន. – digital facsimile from the Linda Hall Library

[1] The pronunciation /ˈjuːlər/ is incorrect. "Euler", Oxford English Dictionary, second edition, Oxford University Press, 1989 "Euler", Merriam–Webster's Online Dictionary, 2009. "Euler, Leonhard", The American Heritage Dictionary of the English Language, fourth edition, Houghton Mifflin Company, Boston, 2000. Peter M. Higgins (2007). Nets, Puzzles, and Postmen: An Exploration of Mathematical Connections. Oxford University Press. p. 43.

[function-2] Dunham, William (1999). Euler: The Master of Us All. The Mathematical Association of America. p. 17.

[volumes-3] ៣,០ ^៣,១ Finkel, B.F. (1897). "Biography- Leonard Euler". The American Mathematical Monthly 4 (12). DOI:10.2307/2968971.

[Laplace-4] Dunham, William (1999). Euler: The Master of Us All. The Mathematical Association of America. xiii. "Lisez Euler, lisez Euler, c'est notre maître à tous."

[theology-5] Euler, Leonhard (1960). "Rettung der Göttlichen Offenbahrung Gegen die Einwürfe der Freygeister". Leonhardi Euleri Opera Omnia (series 3) 12.

[childhood-6] James, Ioan (2002). Remarkable Mathematicians: From Euler to von Neumann. Cambridge. p. 2. ល.ស.ប.អ. 0-521-52094-0.

[7] Translation of Euler's dissertation in English by Ian Bruce

[prize-8] ៨,០ ^៨,១ Calinger, Ronald (1996). "Leonhard Euler: The First St. Petersburg Years (1727–1741)". Historia Mathematica 23 (2). DOI:10.1006/hmat.1996.0015.

[stpetersburg-9] Calinger, Ronald (1996). "Leonhard Euler: The First St. Petersburg Years (1727–1741)". Historia Mathematica 23 (2). DOI:10.1006/hmat.1996.0015.

[medic-10] Calinger, Ronald (1996). "Leonhard Euler: The First St. Petersburg Years (1727–1741)". Historia Mathematica 23 (2). DOI:10.1006/hmat.1996.0015.

[promotion-11] Calinger, Ronald (1996). "Leonhard Euler: The First St. Petersburg Years (1727–1741)". Historia Mathematica 23 (2): 128–129. DOI:10.1006/hmat.1996.0015.

[12] Gekker, I.R.; Euler, A.A. (2007). "Leonhard Euler's family and descendants". ជា Bogoliubov, N.N.; Mikhaĭlov, G.K.; Yushkevich, A.P.. Euler and modern science. Mathematical Association of America. ល.ស.ប.អ. 088385564X. , p. 402.

[wife-13] Fuss, Nicolas. "Eulogy of Euler by Fuss". Retrieved 30 August 2006.

[14] "E212 -- Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum". Dartmouth.

[Friedrich-15] ១៥,០ ^១៥,១ ^១៥,២ Dunham, William (1999). Euler: The Master of Us All. The Mathematical Association of America. xxiv–xxv.

[16] Frederick II of Prussia (1927). Letters of Voltaire and Frederick the Great, Letter H 7434, 25 January 1778. Richard Aldington. New York: Brentano's.

[blind-17] Calinger, Ronald (1996). "Leonhard Euler: The First St. Petersburg Years (1727–1741)". Historia Mathematica 23 (2): 154–155. DOI:10.1006/hmat.1996.0015.

[18] Gekker, I.R.; Euler, A.A. (2007). "Leonhard Euler's family and descendants". ជា Bogoliubov, N.N.; Mikhaĭlov, G.K.; Yushkevich, A.P.. Euler and modern science. Mathematical Association of America. ល.ស.ប.អ. 088385564X. , p. 405.

[euler-19] A. Ya. Yakovlev (1983). Leonhard Euler. M.: Prosvesheniye.

[20] (1783). "Eloge de M. Leonhard Euler. Par M. Fuss.". Nova Acta Academia Scientarum Imperialis Petropolitanae 1: 159–212.

[condorcet-21] Marquis de Condorcet. "Eulogy of Euler - Condorcet". Retrieved 30 August 2006.

[22] ទំព័រគំរូ:Findagrave

[Boyer-23] ២៣,០ ^២៣,១ Boyer, Carl B.; Uta C. Merzbach (1991). A History of Mathematics. John Wiley & Sons. pp. 439–445. ល.ស.ប.អ. 0-471-54397-7.

[pi-24] Wolfram, Stephen. "Mathematical Notation: Past and Future". Retrieved August 2006. {{cite web}}: Check date values in: |accessdate= (help)

[Basel-25] ២៥,០ ^២៥,១ Wanner, Gerhard; Harrier, Ernst (March 2005). Analysis by its history (1st រ.រ.). Springer. p. 62.

[Feynman-26] Feynman, Richard (June 1970). "Chapter 22: Algebra". The Feynman Lectures on Physics: Volume I. p. 10.

[MathInt-27] ២៧,០ ^២៧,១ Wells, David (1990). "Are these the most beautiful?". Mathematical Intelligencer 12 (3): 37–41. DOI:10.1007/BF03024015.
Wells, David (1988). "Which is the most beautiful?". Mathematical Intelligencer 10 (4): 30–31. DOI:10.1007/BF03023741.
See also: Peterson, Ivars. "The Mathematical Tourist". Archived from the original on 2007-03-31. Retrieved March 2008. {{cite web}}: Check date values in: |accessdate= (help)

[analysis-28] Dunham, William (1999). "3,4". Euler: The Master of Us All. The Mathematical Association of America.

[numbertheory-29] Dunham, William (1999). "1,4". Euler: The Master of Us All. The Mathematical Association of America.

[30] Caldwell, Chris. The largest known prime by year

[bridge-31] ៣១,០ ^៣១,១ Alexanderson, Gerald (July 2006). "Euler and Königsberg's bridges: a historical view". Bulletin of the American Mathematical Society 43. DOI:10.1090/S0273-0979-06-01130-X.

[32] Peter R. Cromwell (1997). Polyhedra. Cambridge: Cambridge University Press. pp. 189–190.

[33] Alan Gibbons (1985). Algorithmic Graph Theory. Cambridge: Cambridge University Press. p. 72.

[Cauchy-34] Cauchy, A.L. (1813). "Recherche sur les polyèdres—premier mémoire". Journal de l'Ecole Polytechnique 9 (Cahier 16): 66–86.

[Lhuillier-35] L'Huillier, S.-A.-J. (1861). "Mémoire sur la polyèdrométrie". Annales de Mathématiques 3: 169–189.

[music-36] Calinger, Ronald (1996). "Leonhard Euler: The First St. Petersburg Years (1727–1741)". Historia Mathematica 23 (2): 144–145. DOI:10.1006/hmat.1996.0015.

[37] Youschkevitch, A P; Biography in Dictionary of Scientific Biography (New York 1970–1990).

[optics-38] Home, R.W. (1988). "Leonhard Euler's 'Anti-Newtonian' Theory of Light". Annals of Science 45 (5): 521–533. DOI:10.1080/00033798800200371.

[logic-39] Baron, M. E.; A Note on The Historical Development of Logic Diagrams. The Mathematical Gazette: The Journal of the Mathematical Association. Vol LIII, no. 383 May 1969.

[១]

[២]

[៣]

[៤]

[៥]

[៦]

[៧]

[៨]

[៩]

[១០]

[១១]

[១២]

[១៣]

[១៤]

[១៥]

[១៦]

[១៧]

[១៨]

[១៩]

[២០]

[២១]

[២២]

[២៣]

[២៤]

[២៥]

[២៦]

[២៧]

[២៨]

[២៩]

[៣០]

[៣១]

[៣២]

[៣៣]

[៣៤]

[៣៥]

[៣៦]

[៣៧]

[៣៨]

[៣៩]

លេអុនហាដ អយល័រ

ឆាក​ជីវិត

បឋមកាល

ជីវិត​នៅ​​សាំង​ពេទ័របួគ៌

ជីវិត​នៅ​ប៊ែរឡាំង

ពិការភាព​ភ្នែក

ការ​ត្រលប់​ទៅ​កាន់​រុស្ស៊ី​វិញ

វិភាគទាន​ក្នុង​វិស័យគណិតវិទ្យា​និង​រូបវិទ្យា

និមិត្តសញ្ញា​គណិតវិទ្យា

វិភាគ

ទ្រឹស្ដីនព្វន្ត​

ទ្រឹស្ដីបទ​ក្រាប

គណិតវិទ្យា​អនុវត្តន៍

រូបវិទ្យា​និង​តារាវិទ្យា