반-암시적 오일러 방법

수학에서, 반-암시적 오일러 방법 또는 사교 오일러, 반-명시적 오일러, 오일러-크로머, 그리고 뉴턴-스토머-베렛(NSV) 방법은 고전역학의 상미분방정식의 계인 해밀턴 방정식을 풀기 위한 오일러 방법의 수정이다. 이것은 사교 적분이고 따라서 일반적인 오일러 방법보다 더 좋은 결과를 얻는다.

반-암시적 오일러 방법은 다음의 형태의 미분방정식 쌍에 적용할 수 있다:

${\displaystyle {dx \over dt}=f(t,v)}$

${\displaystyle {dv \over dt}=g(t,x),}$

이 때, f와 g는 두어진 함수이고, x와 v는 스칼라일 수도 있고, 벡터일 수도 있다. 해밀턴 역학에서 운동 방정식은 해밀토니안이 다음의 형태를 가질 때, 이 형태를 가진다:

${\displaystyle H=T(t,v)+V(t,x).\,}$

이 미분방정식은 다음의 초기값으로 풀 수 있다

${\displaystyle x(t_{0})=x_{0},\qquad v(t_{0})=v_{0}.}$

반-암시적 오일러 방법은 다음을 반복함으로 이산적 근사치를 얻는다

${\displaystyle {\begin{aligned}v_{n+1}&=v_{n}+g(t_{n},x_{n})\,\Delta t\\[0.3em]x_{n+1}&=x_{n}+f(t_{n},v_{n+1})\,\Delta t\end{aligned}}}$

여기서 Δt는 한 단계의 시간 간격이고 t_n = t₀ + nΔt는 n단계 뒤의 시간이다.

일반적인 오일러 방법과의 차이는 오일러 방법은 x_n+1의 방정식에서 v_n을 사용하는 반면에 반-암시적 오일러 방법은 v_n+1을 사용한다는 점이다.

${\displaystyle (x_{n+1},v_{n+1})}$

${\displaystyle {\begin{aligned}x_{n+1}&=x_{n}+f(t_{n},v_{n})\,\Delta t\\[0.3em]v_{n+1}&=v_{n}+g(t_{n},x_{n+1})\,\Delta t\end{aligned}}}$

이것은 유사한 속성을 가진다.

반-암시적 오일러는 일반적인 오일러 방법처럼 일차 적분자이다. 이것은 전역오차가 Δt차 라는 것을 의미한다. 하지만 반-암시적 오일러 방법은 일반적인 오일러 방법과는 달리 사교 적분자이다. 결과적으로 반-암시적 오일러 방법은 에너지를 거의 보존한다 (해밀토니안이 시간에 무관할 때). 자주 일반적인 오일러 방법을 사용할 때 에너지가 급격하게 증가하기 때문에 매우 부정확하다.

반-암시적 오일러 방법의 두 변종을 교대로 사용하면 단순화 된 스토머-베렛 적분과 약간 다르게 단순화된 도약적분으로 이끌어, 오차의 차수와 에너지 보존의 차수를 늘린다.

반-암시적 오일러 방법의 안정성 영역이 Niiranen^[1] 에 의해 제시되었지만 반-암시적 오일러는 그의 논문에서 대칭 오일러로 잘못 알려졌다. 반-암시적 방법은 특성 방정식의 복소근이 아래에 나타난 원에 있을 때 시뮬레이션 시스템을 정확히 모델링한다. 실근의 경우, 안정성 영역은  ${\displaystyle s>-2/\Delta t}$

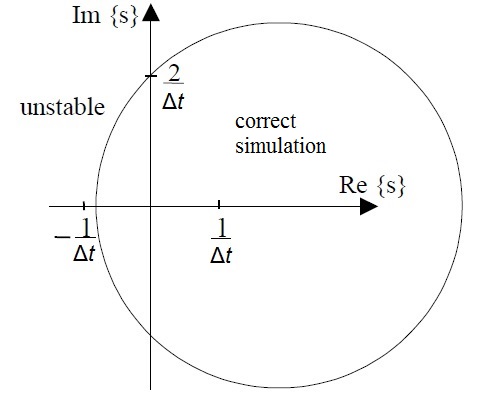
볼 수 있듯이 반-암시적 방법은 근이 평면의 왼쪽 반에 있는 안정한 시스템과 근이 평면의 오른쪽 반에 있는 불안정한 시스템 둘 다 정확히 시뮬레이션할 수 있다. 이것은 일반적인 오일러 방법과 역 오일러 방법보다 확실한 이점이다. 일반적인 오일러 방법은 근의 음의 실수부분이 허수 축에 가까울 때 실제 시스템보다 덜 저동이 걸리고, 역 오일러 방법은 시스템이 평면의 오른쪽 절반에서도 시스템이 안정하다고 나타낸다.

훅 법칙을 만족하는 용수철의 움직임이 다음과 같이 주어졌을 때:

${\displaystyle {\begin{aligned}{\frac {dx}{dt}}&=v(t)\\[0.2em]{\frac {dv}{dt}}&=-{\frac {k}{m}}\,x=-\omega ^{2}\,x.\end{aligned}}}$

이 방정식의 반-오일러 방법은 다음과 같다:

${\displaystyle {\begin{aligned}v_{n+1}&=v_{n}-\omega ^{2}\,x_{n}\,\Delta t\\[0.2em]x_{n+1}&=x_{n}+v_{n+1}\,\Delta t.\end{aligned}}}$

반복은 수정된 에너지 함수 ${\displaystyle E_{h}(x,v)={\tfrac {1}{2}}\left(v^{2}+\omega ^{2}\,x^{2}-\omega ^{2}\Delta t\,vx\right)}$${\displaystyle O(\Delta t)}$. 정확한 각진동수 ${\displaystyle \omega }$는 ${\displaystyle 1+{\tfrac {1}{24}}\omega ^{2}\Delta t^{2}+O(\Delta t^{4})}$.

• Hairer, Ernst; Lubich, Christian; Wanner, Gerhard (2003). “Geometric numerical integration illustrated by the Störmer/Verlet method”. 《Acta Numerica》 12: 399–450. doi:10.1017/S0962492902000144. 
• Giordano, Nicholas J.; Hisao Nakanishi (July 2005). 《Computational Physics》 2판. Benjamin Cummings. ISBN 0-13-146990-8. 
• MacDonald, James. “The Euler-Cromer method”. University of Delaware. 2013년 11월 4일에 원본 문서에서 보존된 문서. 2013년 4월 11일에 확인함. 
• Vesely, Franz J. (2001). 《Computational Physics: An Introduction》 2판. Springer. 117쪽. ISBN 978-0-306-46631-1.