 ŪĒĄŪÜ®Ž†ąŽßąžĚīžė§žä§ ž†ēŽ¶¨žĚė ŽŹĄŪēī
ŪĒĄŪÜ®Ž†ąŽßąžĚīžė§žä§ ž†ēŽ¶¨žĚė ŽŹĄŪēī
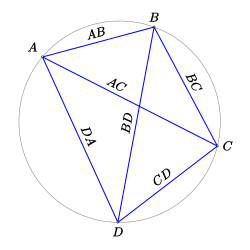
ÍłįŪēėŪēôžóźžĄú ŪĒĄŪÜ®Ž†ąŽßąžĚīžė§žä§ ž†ēŽ¶¨(PtolemaeusŚģöÁźÜ, žėĀžĖī: Ptolemy's theorem) ŽėźŽäĒ ŪÜ®Ž†ąŽĮł ž†ēŽ¶¨(PtolemyŚģöÁźÜ)ŽäĒ žõźžóź Žāīž†ĎŪēėŽäĒ žā¨ÍįĀŪėēžĚė ŽĎź ŽĆÄÍįĀžĄ†žĚė ÍłłžĚīžĚė Í≥ĪžĚī ŽĎź žĆćžĚė ŽĆÄŽ≥ÄžĚė ÍłłžĚīžĚė Í≥ĪžĚė Ūē©Í≥ľ ÍįôŽč§ŽäĒ ž†ēŽ¶¨žĚīŽč§.
ž†ēžĚė
ŪĒĄŪÜ®Ž†ąŽßąžĚīžė§žä§ ž†ēŽ¶¨žóź ŽĒįŽ•īŽ©ī, Žāīž†Ď žā¨ÍįĀŪėē  žóź ŽĆÄŪēėžó¨, Žč§žĚĆžĚī žĄĪŽ¶ĹŪēúŽč§.
žóź ŽĆÄŪēėžó¨, Žč§žĚĆžĚī žĄĪŽ¶ĹŪēúŽč§.

žĚīŽäĒ žľÄžĚīžčúžĚė ž†ēŽ¶¨žĚė ŪäĻžąėŪēú Í≤ĹžöįžĚīŽč§.
ž¶ĚŽ™Ö
žāľÍįĀŪėēžĚė ŽčģžĚƞ̥ ŪÜĶŪēú ž¶ĚŽ™Ö
 žāľÍįĀŪėēžĚė ŽčģžĚƞ̥ ŪÜĶŪēú ž¶ĚŽ™ÖžĚė ŽŹĄŪēī
žāľÍįĀŪėēžĚė ŽčģžĚƞ̥ ŪÜĶŪēú ž¶ĚŽ™ÖžĚė ŽŹĄŪēī
žā¨ÍįĀŪėē  žĚė žôłž†ĎžõźžĚė Ūėł
žĚė žôłž†ĎžõźžĚė Ūėł  žôÄ
žôÄ  žĚė žõźž£ľÍįĀžĚė žĄĪžßąžóź žĚėŪēėžó¨
žĚė žõźž£ľÍįĀžĚė žĄĪžßąžóź žĚėŪēėžó¨  žĚīÍ≥†
žĚīÍ≥†  žĚīŽč§. žĄ†Ž∂Ą
žĚīŽč§. žĄ†Ž∂Ą  žúĄžóźžĄú
žúĄžóźžĄú  Ž•ľ ŽßĆž°ĪžčúŪā§ŽäĒ ž†ź
Ž•ľ ŽßĆž°ĪžčúŪā§ŽäĒ ž†ź  Ž•ľ žě°žěź. Í∑łŽü¨Ž©ī
Ž•ľ žě°žěź. Í∑łŽü¨Ž©ī  žĚīŽč§. ŽĒįŽĚľžĄú, žāľÍįĀŪėē
žĚīŽč§. ŽĒįŽĚľžĄú, žāľÍįĀŪėē  žôÄ
žôÄ  ŽäĒ ŽčģžĚĆžĚīÍ≥†, žāľÍįĀŪėē
ŽäĒ ŽčģžĚĆžĚīÍ≥†, žāľÍįĀŪėē  žôÄ
žôÄ  žó≠žčú ŽčģžĚĆžĚīŽĮÄŽ°ú,
žó≠žčú ŽčģžĚĆžĚīŽĮÄŽ°ú,

žôÄ

ÍįÄ žĄĪŽ¶ĹŪēúŽč§.  žĚīŽĮÄŽ°ú
žĚīŽĮÄŽ°ú

žĚīŽč§.
Žįėž†ĄžĚĄ ŪÜĶŪēú žó≠ž¶ĚŽ™Ö
 Žįėž†ĄžĚĄ ŪÜĶŪēú ž¶ĚŽ™ÖžĚė ŽŹĄŪēī
Žįėž†ĄžĚĄ ŪÜĶŪēú ž¶ĚŽ™ÖžĚė ŽŹĄŪēī
ž§Ďžč¨žĚī  žĚł Žč®žúĄžõźžóź ŽĆÄŪēú Žįėž†Ąžóź ŽĆÄŪēú
žĚł Žč®žúĄžõźžóź ŽĆÄŪēú Žįėž†Ąžóź ŽĆÄŪēú  žĚė žÉĀžĚĄ
žĚė žÉĀžĚĄ  žĚīŽĚľÍ≥† Ūēėžěź. Í∑łŽü¨Ž©ī
žĚīŽĚľÍ≥† Ūēėžěź. Í∑łŽü¨Ž©ī  žĚÄ žĄúŽ°ú Žč§Ž•ł Í≥ĶžĄ†ž†źžĚīŽ©į,
žĚÄ žĄúŽ°ú Žč§Ž•ł Í≥ĶžĄ†ž†źžĚīŽ©į,  žĚÄ
žĚÄ  žôÄ
žôÄ  žā¨žĚīžĚė ž†źžĚīŽč§. Žįėž†ĄžĚė žĄĪžßąžóź žĚėŪēėžó¨
žā¨žĚīžĚė ž†źžĚīŽč§. Žįėž†ĄžĚė žĄĪžßąžóź žĚėŪēėžó¨



žĚīŽ©į,  žĚīŽĮÄŽ°ú,
žĚīŽĮÄŽ°ú,

ÍįÄ žĄĪŽ¶ĹŪēúŽč§.
ŽĒįŽ¶Ąž†ēŽ¶¨
žāľÍįĀ Ūē®žąė Ūē≠ŽďĪžčĚ
ŪĒĄŪÜ®Ž†ąŽßąžĚīžė§žä§ ž†ēŽ¶¨žóźžĄú Ūēú ŽĆÄÍįĀžĄ†žĚī Žāīž†ĎžõźžĚė žßÄŽ¶ĄžĚł Í≤ĹžöįŽäĒ ŽĎź ÍįĀžĚė Ūē©žĚė žā¨žĚł Ūē®žąėžóź ŽĆÄŪēú Ūē≠ŽďĪžčĚÍ≥ľ ŽŹôžĻėžĚīŽč§.[1]:309, Historical note 10.9.2.1 ž¶Č, Žāīž†Ď žā¨ÍįĀŪėē  žĚė ŽĆÄÍįĀžĄ†
žĚė ŽĆÄÍįĀžĄ†  ÍįÄ Žāīž†ĎžõźžĚė ž§Ďžč¨
ÍįÄ Žāīž†ĎžõźžĚė ž§Ďžč¨  Ž•ľ žßÄŽāúŽč§Í≥† Ūēėžěź. ŪéłžĚėžÉĀ Žāīž†ĎžõźžĚė ŽįėžßÄŽ¶ĄžĚī 1žĚīŽĚľÍ≥† Ūēėžěź. ŽėźŪēú
Ž•ľ žßÄŽāúŽč§Í≥† Ūēėžěź. ŪéłžĚėžÉĀ Žāīž†ĎžõźžĚė ŽįėžßÄŽ¶ĄžĚī 1žĚīŽĚľÍ≥† Ūēėžěź. ŽėźŪēú  žĚīÍ≥†
žĚīÍ≥†  ŽĚľÍ≥† Ūēėžěź. Í∑łŽü¨Ž©ī
ŽĚľÍ≥† Ūēėžěź. Í∑łŽü¨Ž©ī






žĚīŽĮÄŽ°ú, ŪĒĄŪÜ®Ž†ąŽßąžĚīžė§žä§ ž†ēŽ¶¨žóź žĚėŪēėžó¨

ÍįÄ žĄĪŽ¶ĹŪēúŽč§.
ŪĒĄŪÜ®Ž†ąŽßąžĚīžė§žä§ ž†ēŽ¶¨žĚė žó≠
ŪĒĄŪÜ®Ž†ąŽßąžĚīžė§žä§ ž†ēŽ¶¨žĚė žó≠ ŽėźŪēú žĄĪŽ¶ĹŪēúŽč§. ž¶Č, žā¨ÍįĀŪėē  ÍįÄ
ÍįÄ

Ž•ľ ŽßĆž°ĪžčúŪā®Žč§Ž©ī, Žāīž†Ď žā¨ÍįĀŪėēžĚīŽč§.
ŪĒĄŪÜ®Ž†ąŽßąžĚīžė§žä§ Ž∂ÄŽďĪžčĚ
ŪĒĄŪÜ®Ž†ąŽßąžĚīžė§žä§ Ž∂ÄŽďĪžčĚ(PtolemaeusšłćÁ≠ČŚľŹ, žėĀžĖī: Ptolemy's inequality)žóź ŽĒįŽ•īŽ©ī, žěĄžĚėžĚė žā¨ÍįĀŪėē  žóź ŽĆÄŪēėžó¨, Žč§žĚĆžĚī žĄĪŽ¶ĹŪēúŽč§.
žóź ŽĆÄŪēėžó¨, Žč§žĚĆžĚī žĄĪŽ¶ĹŪēúŽč§.

ŽėźŪēú, ŽďĪŪėłÍįÄ žĄĪŽ¶ĹŪē† ŪēĄžöĒž∂©Ž∂Ąž°įÍĪīžĚÄ Žāīž†Ď žā¨ÍįĀŪėēžĚīŽč§.
Ž≥īŽč§ žĚľŽįėž†ĀžúľŽ°ú, ŪŹČŽ©ī žúĄ žěĄžĚėžĚė ŽĄ§ ž†ź  žóź ŽĆÄŪēėžó¨, žúĄžôÄ ÍįôžĚÄ Ž∂ÄŽďĪžčĚžĚī žĄĪŽ¶ĹŪēėŽ©į, ŽėźŪēú žĚīŽď§žóź ŽĆÄŪēėžó¨ Žč§žĚĆ ŽĎź ž°įÍĪīžĚī žĄúŽ°ú ŽŹôžĻėžĚīŽč§.[1]:309, Proposition 10.9.2
žóź ŽĆÄŪēėžó¨, žúĄžôÄ ÍįôžĚÄ Ž∂ÄŽďĪžčĚžĚī žĄĪŽ¶ĹŪēėŽ©į, ŽėźŪēú žĚīŽď§žóź ŽĆÄŪēėžó¨ Žč§žĚĆ ŽĎź ž°įÍĪīžĚī žĄúŽ°ú ŽŹôžĻėžĚīŽč§.[1]:309, Proposition 10.9.2
- Žč§žĚĆ ÍįÄžöīŽćį ŪēėŽāėÍįÄ žĄĪŽ¶ĹŪēúŽč§.



- Í≥Ķžõźž†źžĚīÍĪįŽāė Í≥ĶžĄ†ž†źžĚīŽč§.
žó≠žā¨
Í≥†ŽĆÄ Í∑łŽ¶¨žä§žĚė ž≤úŽ¨łŪēôžěźžĚīžěź žąėŪēôžěźžĚł ŪĀīŽĚľžöįŽĒĒžė§žä§ ŪĒĄŪÜ®Ž†ąŽßąžĚīžė§žä§ŽäĒ žĚī ž†ēŽ¶¨Ž•ľ ž†ÄžĄú „ÄäžēĆŽßąÍ≤Ćžä§Ūäł„Äčžóź ŽďĪžě•ŪēėŽäĒ ŪėĄŪĎúŽ•ľ ŽßĆŽďúŽäĒ Žćį žā¨žö©ŪēėžėÄŽč§.[1]:309, Historical note 10.9.2.1
ÍįôžĚī Ž≥īÍłį
ÍįĀž£ľ
žôłŽ∂Ä ŽßĀŪĀ¨



























































