수학에서 넓은 의미의 회전에 대해서는
회전 문서를 참고하십시오.
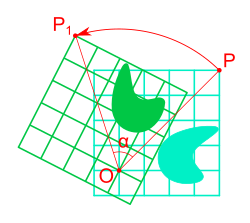
2차원에서 점 O 에 대한 회전 회전 (回轉, 영어 : rotation ) 또는 회전 이동 (回轉 移動)은 기하학 에서 하나의 점을 중심으로 같은 각도 회전시키는 함수를 가리킨다. 고정점 이 있는 아핀 변환 이다. 한 고정점을 강체 (rigid body)로 가진다고 할 수 있다. 회전은 각도 를 가지는데 시계 방향을 음수, 반시계 방향을 양수로 표현한다. 회전 이동은 고정점이 없는 평행 이동 이나 고정점의 집합이 초평면 인 대칭 이동 (반사)과는 다르다.
회전은 수학적으로 사상 (map)이다. 고정점을 가지는 모든 회전은 공간에서 회전군 이라는 합성 으로 군 을 이룬다. 하지만 역학 이나 물리학 에서는 회전의 개념을 좌표 변환 으로 받아들인다.
회전군은 고정점 에 대한 회전의 리군 이다. 고정점은 '회전의 중심 '이라 하며 대부분의 경우 원점 으로 생각한다. 회전군은 군의 작용 에서 점이 안정자군 이다.
회전의 축(axis)은 고정점의 직선 이다. n > 2
회전의 평면 (plane)은 회전에 대한 불변량 인 평면 이다. 축과는 다르게 각 점들이 서로 고정되어 있지 않다. 회전축과 회전의 평면은 직교 한다.회전의 표현(representation)은 대수적이나 기하학적으로 회전 사상을 매개변수로 표시(parametrize)하는 형식이다. 군의 표현 과는 반대이다.
점들의 아핀 공간 이나 벡터 공간 에서 회전은 항상 확실히 구별할 수는 없다. 전자는 아핀 회전, 후자는 벡터 회전을 말한다.
이차원에 있어서 회전을 생각할 때 회전각 이라는 각도 를 결정할 수 있는데, 원점 을 중심으로 각 θ만큼 반시계방향 회전했을 때의 θ이다. 회전을 기술하기 위해 행렬 과 복소수 를 이용한다.
회전하는 점 (x, y)를 벡터로 생각해서 각 θ 회전시켜 (x', y')이 되는 것을 행렬의 곱셈으로 다음과 같이 나타낼 수 있다.
[
x
′
y
′
]
=
[
cos
θ
−
sin
θ
sin
θ
cos
θ
]
[
x
y
]
{\displaystyle {\begin{bmatrix}x'\\y'\end{bmatrix}}={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}}
즉, 다음과 같다.
x
′
=
x
cos
θ
−
y
sin
θ
y
′
=
x
sin
θ
+
y
cos
θ
{\displaystyle {\begin{aligned}x'&=x\cos \theta -y\sin \theta \\y'&=x\sin \theta +y\cos \theta \end{aligned}}}
두 벡터
[
x
y
]
,
[
x
′
y
′
]
{\displaystyle {\begin{bmatrix}x\\y\end{bmatrix}},\quad {\begin{bmatrix}x'\\y'\end{bmatrix}}}
는 같은 크기를 가진다.
평면 상의 점 (x,y)는 복소수
z
=
x
+
i
y
{\displaystyle z=x+iy}
로 표현된다. 각 θ 회전했을 때를 오일러 공식 을 써서 전개하면 다음과 같다.
e
i
θ
z
=
(
cos
θ
+
i
sin
θ
)
(
x
+
i
y
)
=
(
x
cos
θ
+
i
y
cos
θ
+
i
x
sin
θ
−
y
sin
θ
)
=
(
x
cos
θ
−
y
sin
θ
)
+
i
(
x
sin
θ
+
y
cos
θ
)
=
x
′
+
i
y
′
{\displaystyle {\begin{aligned}e^{i\theta }z&=(\cos \theta +i\sin \theta )(x+iy)\\&=(x\cos \theta +iy\cos \theta +ix\sin \theta -y\sin \theta )\\&=(x\cos \theta -y\sin \theta )+i(x\sin \theta +y\cos \theta )\\&=x'+iy'\end{aligned}}}
즉 얻은 결과가 앞과 같다.
수학에서 넓은 의미의 회전에 대해서는 회전 문서를 참고하십시오.
U(1) 문서를 참고하십시오.
