Смит–Вотерманов алгоритам

Класа	Порамнување на низи
Најлош случај	${\displaystyle O(mn)}$
Просторна сложеност во најлош случај	${\displaystyle O(mn)}$

Смит–Вотермановиот алгоритам е алгоритам кој служи за локално порамнување на низи, т.е., за утврдување на слични региони меѓу две нуклеотидни или аминокиселински низи. Со овој метод не се врши споредување на целосната низа, туку се споредуваат сегменти со произволна должина и се оптимизира коефициентот на сличност.

Алгоритмот бил предложен од страна на Темпл Ф. Смит и Мајкл С. Вотерман во 1981 година.^[1] Тој е варијација на Нидлман–Вуншовиот алгоритам и како него претставува алгоритам на динамичко програмирање. Како таков, тој гарантира пронаоѓање на оптимално локално порамнување на низи со системот за бодување кој се користи (како што се матрицата на замена и системот за бодување на празнини). Главната разлика со Нидлман–Вуншовиот алгоритам е што ќелиите со негативни бодови се заменуваат со вредност нула, што прави да позитивно бодуваните локални порамнувања станат видливи. Постапката на следење наназад кон потеклото започнува со ќелијата на матрицата која е највисоко бодувана и продолжува до ќелијата со бод нула, што го дава највисоко бодуваното локално порамнување. Поради својата квадратна комплексност во времето и просторот, овој алгоритам често не може практично да биде применет за поголеми проблеми, па е заменет со помалку општи, но пресметковно поефикасни алтернативи, како што се (Гото, 1982),^[2] (Алтшул и Ериксон, 1986),^[3] и (Маерс и Милер, 1988).^[4]

Во 1970 година, Саул Б. Нидлман и Кристијан Д, Вунш, предложиле евристички хомолошки алгоритам за порамнување на низи, исто така познат како Нидлман–Вуншов алгоритам.^[5] Станува збор за алгоритам за глобално порамнување на низи, за кого се потребни ${\displaystyle O(mn)}$ пресметковни чекори (${\displaystyle m}$ и ${\displaystyle n}$ се должините на двете низи кои треба да се порамнат). Алгоритмот користи итеративна пресметка на матрица за прикажување на глобално порамнување на низите. Во текот на наредната деценија, Санков,^[6] Рајчерт,^[7] Бејер^[8] и другите формулирале алтернативни евристички алгоритми за анализа на генски низи. Селерс вовел систем за мерење на низна дистанца.^[9] Во 1976 година, Вотерман et al. го додале концептот на празнини во оригиналниот мерен систем.^[10] Во 1981 година, Смит и Вотерман го објавиле нивниот Смит–Вотерманов алгоритам за пресметување на локално порамнување на низи.

Смит–Вотермановиот алгоритам изискува прилично долго време: за да се порамнат две низи со должини ${\displaystyle m}$ и ${\displaystyle n}$, потребно е ${\displaystyle O(mn)}$ време. Гото^[2] и Алтшул^[3] го оптимизирале алгоритмот на ${\displaystyle O(mn)}$ чекори. Просторната сложеност била оптимизирана од страна на Маерс и Милер^[4] од ${\displaystyle O(mn)}$ на ${\displaystyle O(n)}$ (линеарна), каде ${\displaystyle n}$ е должината на пократката низа, за случајот кога е потребно само едно од многуте можни оптимални порамнувања.

Во текот на изминатите три децении, проектите за секвенционирање на геномите на различни организми создадоа огромна количина на податоци за генски и белковински низи, за кои е потребна пресметковна анализа. Порамнувањата на низите ги покажува односите помеѓу гените или белковините (белковините), што доведува до подобро разбирање на нивната хомологија и функционалност. Порамнувањето на низите исто така може да открие сочувани домени и сочувани низни мотиви.

Една мотивација за локално порамнување на низи е потешкотијата во добивањето на точни порамнувања во регионите со ниско ниво на сличност помеѓу далечно сродните биолошки низи, бидејќи мутациите во текот на еволуцијата имаат создадено премногу „шум“ за да може да се изврши споредба на овие региони. Локалното порамнување потполно ги избегнува таквите региони и се фокусира само на оние со позитивни бодови, односно оние со еволутивно сочуван сигнал за сличност. Предуслов за локалното порамнување е негативен очекуван бод. Очекуваниот бод е дефиниран како просечен бод кој системот за бодување (матрицата на замена и системот за бодување на празнини) ќе даде случајна низа.

Друга мотивација за користење на локалните порамнувања е што постои сигурен статистички модел (развиен од Карлин и Алтшул) за оптимални локални порамнувања. Порамнувањето на несродните низи има тенденција да создаде оптимални бодови за локално порамнување кои следат екстремна дистрибуција на вредности. Ова својство им овозможува на програмите да создадат очекувана вредност за оптимално локално порамнување на две низи, што е мерка за тоа колку често две несродни низи ќе создадат оптимално локално порамнување чиј бод е поголем или еднаков на набљудуваниот бод. Многу ниска очекувана вредност означува дека двете низи за кои станува збор може да бидат хомологни, што значи дека тие може да споделуваат заеднички предок.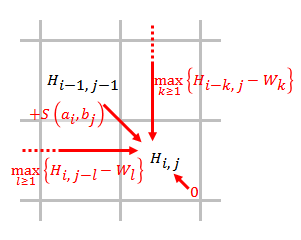

Нека ${\displaystyle A=a_{1}a_{2}...a_{n}}$ и ${\displaystyle B=b_{1}b_{2}...b_{m}}$ се низи кои треба да бидат порамнети, каде ${\displaystyle n}$ и ${\displaystyle m}$ се должините на ${\displaystyle A}$ и ${\displaystyle B}$, соодветно.

1. Одреди ги матрицата на замена и системот за бодување на празнини.
   • ${\displaystyle s(a,b)}$ - бод на сличност на елементите кои ги сочинуваат двете низи
   • ${\displaystyle W_{k}}$ - Казнен бод за празнина со должина ${\displaystyle k}$
2. Конструирај матрица на бодување ${\displaystyle H}$ и иницијализирај ги првиот ред и првата колона. Димензијата на матрицата за бодување е ${\displaystyle (n+1)*(m+1)}$. Индексирањето е засновано на нула.

   ${\displaystyle H_{k0}=H_{0l}=0\quad for\quad 0\leq k\leq n\quad and\quad 0\leq l\leq m}$

3. Пополни ја матрицата на бодување со користење на следната формула:

   ${\displaystyle H_{ij}=\max {\begin{cases}H_{i-1,j-1}+s(a_{i},b_{j}),\\\max _{k\geq 1}\{H_{i-k,j}-W_{k}\},\\\max _{l\geq 1}\{H_{i,j-l}-W_{l}\},\\0\end{cases}}\qquad (1\leq i\leq n,1\leq j\leq m)}$

   каде

   ${\displaystyle H_{i-1,j-1}+s(a_{i},b_{j})}$ е бодот на порамнување на ${\displaystyle a_{i}}$ и ${\displaystyle b_{j}}$,

   ${\displaystyle H_{i-k,j}-W_{k}}$ е бодот ако ${\displaystyle a_{i}}$ е крајот на празнина со должина ${\displaystyle k}$,

   ${\displaystyle H_{i,j-l}-W_{l}}$ е бодот ако ${\displaystyle b_{j}}$ е крајот на празнина со должина ${\displaystyle l}$,

   ${\displaystyle 0}$ значи дека нема сличност до ${\displaystyle a_{i}}$ и ${\displaystyle b_{j}}$.

4. Следење назад кон потеклото. Почни со највисокиот бод во матрицата за бодување ${\displaystyle H}$ и следи сѐ до ќелија на матрицата со бод нула.

Смит–Вотермановиот алгоритам порамнува две низи со совпаѓања/несовпаѓања (исто така познати како супституции), вметнувања и бришења. Вметнувањате и бришењате се операции кои означуваат празнини, кои се претставени со цртички. Смит–Вотермановиот алгоритам се состои од неколку чекори:

1. Одредување на матрицата на замена и системот за бодување на празнини. Матрицата на замена доделува бод на секој пар на азотни бази или аминокиселини за совпаѓање или несовпаѓање. Обично совпаѓањата добиваат позитивни бодови, додека несовпаѓањата добиваат ниски бодови. Функцијата за казнени бодови за празнина ги одредува казнените бодови за отворање или екстензија на празнини.
2. Иницијализирање на матрицата на бодување. Димензиите на матрицата на бодување се 1+должина во однос на секоја низа соодветно. Сите елементи на првиот ред и првата колона имаат вредност нула. Дополнителните прв ред и прва колона овозможуваат да се порамнат две низи во која било позиција, а давањето на вредност нула прави да терминалната празнина не добие казнени бодови.
3. Бодување. Бодувањето се врши на секој елемент од лево надесно и од горе надолу во матрицата. Потоа се разгледуваат резултатите на супституции (дијагонални бодови) или празнини (хоризонтални и вертикални бодови). Доколку ниту еден од бодовите не е позитивен, елементот добива вредност нула. Потоа се забележува највисокиот бод и неговиот извор.
4. Следење назад кон потеклото. Почнувајќи со елементот со највисокиот бод, следењето назад кон потеклото се врши од изворот на секој бод рекурзивно, додека не се дојде до бод со вредност нула. Оние сегменти кои имаат најголеми бодови за сличност, врз основа на дадениот систем за бодување, се добиваат во текот на овој процес. За да го добие второто најдобро локално порамнување, процесот на следењето назад кон потеклото почнува од вториот највисок бод.

Разликата помеѓу Смит–Вотермановиот алгоритам и Нидлман–Вуншовиот алгоритам е што првиот служи за пронаоѓање на оние сегменти во две дадени низи кои имаат сличности, додека вториот целосно ги порамнува двете низи. Сличностите се што и двата алгоритми ги користат концептите на матрица на замена, функција за казнени бодови за празнини, матрица на бодување и процест на следењо назад кон потеклото. Три главни разлики се:

Една од најважните разлики помеѓу двата алгоритма е што во системот на бодување кај Смит–Вотермановиот алгоритам не се даваат негативни бодови. Кога некој елемент има бод помал од нула, тоа значи дека низите до таа позиција немаат никаква сличност; затоа овој елемент се поставува на вредност нула, за да се елиминира влијанието од претходното порамнување. На овој начин, може да се продолжи со пронаоѓање на порамнување во било која позиција која следи потоа.

Првичната матрица на бодување на Смит–Вотермановиот алгоритам овозможува порамнување на кој било сегмент од едната низа со произволна позиција во другата низа. Кај Нидлман–Вуншовиот алгоритам треба да се земе предвид и казнениот бод за последната празнина за целосно да се порамнат низите.

Секоја супституција на азотна база или аминокиселина добива одреден бод. Во принцип, совпаѓањата добиваат позитивни бодови, а несовпаѓањата добиваат релативно ниски бодови. На пример, за РНК-низите, ако совпаѓањата добиваат +1, несовпаѓањата добиваат -1, па тогаш матрицата на замена е:

Оваа матрица на замена може да се опише како: ${\displaystyle s(a_{i},b_{j})={\begin{cases}+1,\quad a_{i}=b_{j}\\-1,\quad a_{i}\neq b_{j}\end{cases}}}$

Различните супституции на азотни бази или аминокиселини може да имаат различни бодови. Матрицата на замена за аминокиселините обично е покомплицирана од онаа за азотните бази.

Казнените бодови за празнина се однесуваат на бодовите за вметнувања и бришења. Едноставна стратегија за казнени бодови за празнини е да се користат фиксни бодови за секоја празнина. Во биологијата, сепак, бодовите треба да бидат различни од практични причини. Од една страна, делумната сличност помеѓу две низи е честа појава; од друга страна, една генска мутација може да резултира со вметнување на една долга празнина. Затоа, долгите празнини обично повеќе се фаворизирани од повеќе расфрлани, кратки празнини. За да се земе предвид оваа разлика, во системот на бодување додадени се концептите на отворање на празнина и екстензија (проширување) на празнина. Бодот за отворање на празнина е обично поголем од бодот за проширување на празнина. На пример, основните параметри во EMBOSS Water се: отворање на празнина = 10, проширување на празнина = 0.5.

Овде ќе стане збор за две чести стратегии за казнени бодови за празнина. Нека ${\displaystyle W_{k}}$ биде функцијата за казнени бодови за празнина со должина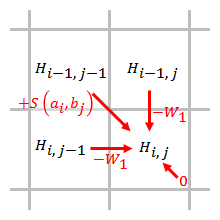 ${\displaystyle k}$:

Линеарната стратегија за казнени бодови за празнина ги има истите бодови за отворање и проширување на празнината:

${\displaystyle W_{k}=kW_{1}}$,

каде ${\displaystyle W_{1}}$ е цената за една празнина.

Казнените бодови за празнина директно се пропорционални со должината на празнината. Кога се користи линеарната стратегија за казнени бодови за празнина, Смит–Вотермановиот алгоритам може да биде поедноставен во следната форма:

${\displaystyle H_{ij}=\max {\begin{cases}H_{i-1,j-1}+s(a_{i},b_{j}),\\H_{i-1,j}-W_{1},\\H_{i,j-1}-W_{1},\\0\end{cases}}}$

Поедноставениот алгоритам користи ${\displaystyle O(mn)}$ чекори. Кога некој елемент се бодува, треба да се земат предвид само казнените бодови од елементите кои се во негова непосредна близина.

Афината стратегија за казнени бодови за празнина одделно ги бодува отворањето на празнина и екстензијата на празнина:

${\displaystyle W_{k}=uk+v\quad (u>0,v>0)}$,

каде ${\displaystyle v}$ е казната за отворање на празнина, а ${\displaystyle u}$ е казната за екстензија на празнина. На пример, казната за празнина со должина 2 е ${\displaystyle 2u+v}$.

Во оригиналниот Смит–Вотерманов алгоритам бил користен произволен систем за казнени бодови за празнина. Овој систем користи ${\displaystyle O(m^{2}n)}$ чекори, поради што е прилично долготраен. Гото ги оптимизирал чекорите за афин систем за казнени бодови за празнина на ${\displaystyle O(mn)}$,^[2] но оптимизираниот алгоритам е способен да пронајде само едно оптимално порамнување, кое не е загарантирано да се пронајде.^[3] Алтшул го има изменето алгоритмот на Гото за да можат да бидат пронајдени сите оптимални порамнувања.^[3] Подоцна, Маерс и Милер покажале дека алгоритмот на Гото и Алтшул може дополнително да биде изменет врз основа на методот објавен од страна на Хиршберг во 1975 година.^[4][11] Алгоритмот на Маерс и Милер може да порамни две низи со употреба на ${\displaystyle O(n)}$ простор, каде ${\displaystyle n}$ е должината на пократката низа.

Да го земеме како пример порамнувањето на ДНК-низите TACGGGCCCGCTAC и TAGCCCTATCGGTCA. Кога се користи линеарна функција за казнени бодови за празнина резултатот е (Порамнувањето е извршено од EMBOSS Water. Матрицата на замена е DNAfull. Казнените бодови за отворање и проширување на празнина се 1.0):

TACGGGCCCGCTA-C
||   | || ||| |
TA---G-CC-CTATC

Кога се користи афината функција за казнени бодови за празнина, резултатот е (Казнените бодови за отворање и проширување на празнина се 5.0 и 1.0, соодветно):

TACGGGCCCGCTA
||   |||  |||
TA---GCC—CTA

Овој пример покажува дека афината функција за казнени бодови за празнина може да помогне да се избегнат расфрлани мали празнини.

Функцијата на матрицата за бодување е да спроведе споредба помеѓу сите компоненти во две низи и да ги евидентира оптималните резултати на порамнувањето. Процесот на бодување го одразува концептот на динамичко програмирање. Конечното оптимално порамнување се наоѓа преку итеративно проширување на растечкото оптимално порамнување. Со други зборови, моменталното оптимално порамнување се генерира со одлучување која патека (совпаѓање/несовпаѓање или внесување на празнина) го дава највисокиот бод од претходното оптимално порамнување. Големината на матрицата е должината на едната низа плус 1 по должината на другата низа плус 1. Дополнителниот прв ред и прва колона служат да се порамни едната низа со било која позиција во другата низа. И на првиот ред и на првата колона им се дава вредност нула, за крајната празнина да не добие казнени бодови. Почетната матрица за бодување е:

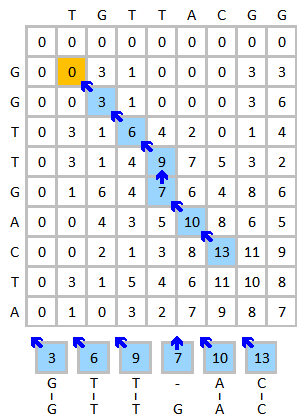
Да го земеме како пример порамнувањето на ДНК-низите TGTTACGG и GGTTGACTA. Со употреба на следниот систем:

• Матрица на замена: ${\displaystyle s(a_{i},b_{j})={\begin{cases}+3,\quad a_{i}=b_{j}\\-3,\quad a_{i}\neq b_{j}\end{cases}}}$
• Казнени бодови за празнина: ${\displaystyle W_{k}=2k}$ (линеарна функција на казнени бодови за празнина од ${\displaystyle W_{1}=2}$)

Се иницијализира и се пополнува матрицата на бодување како што е прикажано подолу. Сликата го прикажува процесот на бодување за трите првите елементи. Жолтата боја ги означува азотните бази кои се разгледуваат. Црвената боја го означува највисокиот можен бод за ќелијата која се бодува.

Крајната матрица на бодување е прикажана подолу налево. Сината боја го покажува највисокиот бод. Забележете дека еден елемент може да добие бод од повеќе од еден елемент, секој ќе формира поинаква патека ако овој елемент се следи наназад. Во случај на повеќе највисоки бодови, следењето наназад треба да се изврши почнувајќи од секој највисок бод. Процесот на следење наназад кон потеклото е прикажан подолу десно. Најдоброто локално порамнување се генерирана во обратна насока.

Завршена матрица на бодување (највисокиот бод е син)	Процес на следење назад кон потеклото и резултат на порамнувањето

Резултатот на порамнувањето на овие две низи е:

G T T - A C
| | |   | |
G T T G A C

• Биоинформатика
• Порамнување на низи
• Нидлман-Вуншов алгоритам
• Левенштајново растојание
• BLAST
• FASTA

1. ↑ Smith, Temple F. & Waterman, Michael S. (1981). „Identification of Common Molecular Subsequences“ (PDF). Journal of Molecular Biology. 147: 195–197. doi:10.1016/0022-2836(81)90087-5. PMID 7265238.
2. ↑ ^{2,0 2,1 2,2} Osamu Gotoh (1982). „An improved algorithm for matching biological sequences“. Journal of Molecular Biology. 162: 705–708. doi:10.1016/0022-2836(82)90398-9.
3. ↑ ^{3,0 3,1 3,2 3,3} Stephen F. Altschul & Bruce W. Erickson (1986). „Optimal sequence alignment using affine gap costs“. Bulletin of Mathematical Biology. 48: 603–616. doi:10.1007/BF02462326.
4. ↑ ^{4,0 4,1 4,2} Miller, Webb; Myers, Eugene (1988). „Optimal alignments in linear space“. Bioinformatics. 4: 11–17. doi:10.1093/bioinformatics/4.1.11.
5. ↑ Saul B. Needleman; Christian D. Wunsch (1970). „A general method applicable to the search for similarities in the amino acid sequence of two proteins“. Journal of Molecular Biology. 48: 443–453. doi:10.1016/0022-2836(70)90057-4. PMID 5420325.
6. ↑ Sankoff D. (1972). „Matching Sequences under Deletion/Insertion Constraints“. Proceedings of the National Academy of Sciences of the United States of America. 69: 4–6. doi:10.1073/pnas.69.1.4. PMC 427531. PMID 4500555.
7. ↑ Thomas A. Reichert; Donald N. Cohen; Andrew K.C. Wong (1973). „An application of information theory to genetic mutations and the matching of polypeptide sequences“. Journal of Theoretical Biology. 42: 245–261. doi:10.1016/0022-5193(73)90088-X.
8. ↑ William A. Beyer, Myron L. Stein, Temple F. Smith, and Stanislaw M. Ulam (1974). „A molecular sequence metric and evolutionary trees“. Mathematical Biosciences. 19: 9–25. doi:10.1016/0025-5564(74)90028-5.CS1-одржување: повеќе имиња: список на автори (link)
9. ↑ Peter H. Sellers (1974). „On the Theory and Computation of Evolutionary Distances“. Journal of Applied Mathematics. 26: 787–793. doi:10.1137/0126070.
10. ↑ M.S Waterman; T.F Smith; W.A Beyer (1976). „Some biological sequence metrics“. Advances in Mathematics. 20: 367–387. doi:10.1016/0001-8708(76)90202-4.
11. ↑ D. S. Hirschberg (1975). „A linear space algorithm for computing maximal common subsequences“. Communications of the ACM. 18: 341–343. doi:10.1145/360825.360861.

• JAligner — Java имплементација на Смит–Вотермановиот алгоритам
• Basic-Algorithms-of-Bioinformatics Applet — аплет кој визуелно го објаснува алгоритмот
• FASTA/SSEARCH
• UGENE Smith-Waterman Search plugin Архивирано на 24 декември 2016 г. — извор со отворен код SSEARCH компатибилна имплементација на алгоритмот со графички интерфејс, напишан во C++
• Opal — SIMD C/C++ библиотека за масовно оптимално порамнување на низи
• diagonalsw — C/C++ имплементација со отворен код со SIMD инструкциски сет (особено SSE4.1) под MIT лиценца
• SSW — C++ библиотека со отворен код која обезбедување на API за SIMD имплементација на Смит–Вотермановиот алгоритам под MIT лиценца
• мелодично порамнување на низи — javascript имплементација за мелодично порамнување на низи