ചാക്രികഗ്രൂപ്പ്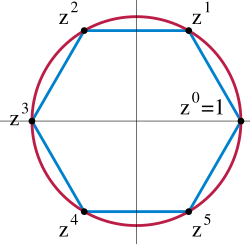

ഇംഗ്ലീഷ് വിലാസം

https://ml.wikipedia.org/wiki/Cyclic_group

ഒരു ഗ്രൂപ്പിലെ എല്ലാ അംഗങ്ങളെയും ഏതെങ്കിലും ഒരു പ്രത്യേക അംഗത്തിന്റെ ഘാതമായി എഴുതാൻ സാധിക്കുമെങ്കിൽ അതിനെ ഒരു ചാക്രികഗ്രൂപ്പ് (Cyclic group) എന്നു വിളിക്കുന്നു. ഈ പ്രത്യേക അംഗത്തെ ഗ്രൂപ്പിന്റെ ജനകം അഥവാ അടിസ്ഥാന അംഗം എന്ന് വിളിക്കുന്നു. (G,•) ഒരു ചാക്രിക ഗ്രൂപ്പ് ആണെന്ന് സങ്കല്പിക്കുക. a എന്ന അംഗം ഗ്രൂപ്പിന്റെ ജനകവും e തൽസമകവുമാണെങ്കിൽ ഗ്രൂപ്പിലെ അംഗങ്ങളെല്ലാം a¹=a, a²=a•a, a³=a•a•a,..., a⁰=e, a^-1, a^-2=a^-1•a^-1... ഇവയിലേതെങ്കിലും ഒന്നായിരിക്കണം. അതായത്, b ഗ്രൂപ്പിലെ ഒരു അംഗമാണെങ്കിൽ b=aⁿ എന്ന തരത്തിൽ n എന്ന പൂർണ്ണസംഖ്യ ഉണ്ടാകും.

ചാക്രികഗ്രൂപ്പുകൾ പരിബദ്ധമോ അനന്തമോ ആകാം. (${\displaystyle \mathbb {Z} _{p}}$,+) ഒരു പരിബദ്ധ ചാക്രികഗ്രൂപ്പാണ്, (${\displaystyle \mathbb {Z} }$,+) ഒരു അനന്ത ചാക്രികഗ്രൂപ്പും. ഒരു ചാക്രികഗ്രൂപ്പിന്‌ ഒന്നിലധികം ജനകങ്ങളുണ്ടാകാം. ഉദാഹരണമായി (${\displaystyle \mathbb {Z} }$,+) എന്ന ചാക്രികഗ്രൂപ്പിന് 1, -1 എന്നിങ്ങനെ രണ്ട് ജനകങ്ങളുണ്ട്. ചാക്രികഗ്രൂപ്പുകളെല്ലാം തന്നെ ക്രമഗ്രൂപ്പുകളാണ്.

ചാക്രികഗ്രൂപ്പുകളുടെ ഉപഗ്രൂപ്പുകളും ചാക്രികഗ്രൂപ്പുകളായിരിക്കും. G എന്നത് N അംഗങ്ങളുള്ള ഒരു ഗ്രൂപ്പാണെങ്കിൽ N ന്റെ ഓരോ ഘടകത്തിനും G യ്ക്ക് അത്രയും അംഗങ്ങളുള്ള കൃത്യം ഒരു ഉപഗ്രൂപ്പുണ്ടാകും. അംഗങ്ങളുടെ എണ്ണം അഭാജ്യസംഖ്യയായിട്ടുള്ള ഏതൊരു ഗ്രൂപ്പും ചാക്രികമായിരിക്കും.

ചാക്രികമല്ലാത്ത ഏറ്റവും ചെറിയ ഗ്രൂപ്പ് ക്ലൈൻ ഗ്രൂപ്പ് ആണ്.

• http://mathworld.wolfram.com/CyclicGroup.html