ą“øą“®ą“¤ą“¾ą“Ŗ ą“Ŗąµą“°ą“ąµą“°ą“æą“Æą“µąµą“Æąµą“¹ą“¤ąµą“¤ą“æą“Øąµą“±ąµ ą“¤ą“¾ą“Ŗą“Øą“æą“²ą“Æąµą“ąµą“ąµ ą“®ą“¾ą“±ąµą“±ą“ ą“µą“°ą“¾ą“¤ąµ ą“Øą“ą“ąµą“ąµą“Øąµą“Ø ą“¤ą“¾ą“Ŗą“ą“¤ą“æą“ ą“Ŗąµą“°ą“ąµą“°ą“æą“Æą“Æą“¾ą“£ąµ ą“øą“®ą“¤ą“¾ą“Ŗą“Ŗąµą“°ą“ąµą“°ą“æą“Æ (Isothermal Process) : Ī T = 0. ą“¤ą“¾ą“Ŗą“ąµą“®ą“¾ą“±ąµą“±ą“¤ąµą“¤ą“æą“²ąµą“ąµ ą“µąµą“Æąµą“¹ą“¤ąµą“¤ą“æą“Øąµ ą“¤ą“¾ą“Ŗą“Øą“æą“² ą“øąµą“„ą“æą“°ą“®ą“¾ą“Æą“æ ą“Øą“æą“²ą“Øą“æąµ¼ą“¤ąµą“¤ą“¾ąµ» ą“¤ą“ąµą“ą“µą“£ąµą“£ą“ ą“øą“¾ą“µą“§ą“¾ą“Øą“ ą“Øą“²ąµą“ą“æą“Æą“¾ą“£ąµ ą“ ą“Ŗąµą“°ą“ąµą“°ą“æą“Æ ą“Øą“ą“ąµą“ąµą“Øąµą“Øą“¤ąµ. ą“ąµą“±ąµą“±ąµą“Ŗą“¾ą“ąµą“®ą“¾ą“Æą“æ ą“¤ą“¾ą“Ŗą“ąµą“®ą“¾ą“±ąµą“±ą“ ą“Øą“ą“ąµą“ą“¾ą“¤ąµą“¤ ą“¤ą“¾ą“Ŗą“¬ą“¦ąµą“§ą“Ŗąµą“°ą“ąµą“°ą“æą“Æ ą“ą“¤ą“æą“Øąµ ą“µą“æą“Ŗą“°ąµą“¤ą“®ą“¾ą“Æ ą“ą“°ąµ ą“Ŗąµą“°ą“ąµą“°ą“æą“Æą“Æą“¾ą“£ąµ. ( Q. = 0). ą“ąµą“°ąµą“ąµą“ą“¤ąµą“¤ą“æąµ½, ą“øą“®ą“¤ą“¾ą“Ŗą“Ŗąµą“°ą“ąµą“°ą“æą“Æą“Æąµ ą“Øą“®ąµą“ąµą“ąµ ą“ą“Ŗąµą“°ą“ą“¾ą“°ą“ ą“Ŗą“±ą“Æą“¾ąµ» ą“ą““ą“æą“Æąµą“
ą“¤ą“¾ą“Ŗą“¬ą“¦ąµą“§ ą“Ŗąµą“°ą“ąµą“°ą“æą“Æą“ą“³ą“æąµ½ ą“ą“²ąµą“²ą“¾ą“Æąµą“Ŗąµą“Ŗąµą““ąµą“: ą“ą“¦ą“¾ą“¹ą“°ą“£ą“ąµą“ąµ¾ą“ą“Æąµ¼ą“Øąµą“Ø ą“ą“ą“Øą“Æąµą“³ąµą“³ ą“Æą“Øąµą“¤ąµą“°ą“ąµą“ąµ¾, ą“ąµą“µą“Øąµą“³ąµą“³ ą“ąµą“¶ą“ąµą“ąµ¾ ą“ą“Øąµą“Øą“æą“µ ą“ąµ¾ą“Ŗąµą“Ŗąµą“ąµ ą“¤ą“¾ą“Ŗą“Øą“æą“² ą“Øą“æą“Æą“Øąµą“¤ąµą“°ą“æą“ąµą“ąµą“Øą“æąµ¼ą“¤ąµą“¤ąµą“£ąµą“ą“¤ą“¾ą“Æ ą“ą“²ąµą“²ą“¾ ą“µąµą“Æąµą“¹ą“ąµą“ą“³ą“æą“²ąµą“ ą“øą“®ą“¤ą“¾ą“Ŗą“Ŗąµą“°ą“ąµą“°ą“æą“Æą“ąµ¾ ą“øą“ą“ą“µą“æą“ąµą“ąµą“Øąµą“Øąµ. ą“ą“æą“² ą“¤ą“¾ą“Ŗą“ą“ąµą“ą“æą“Øąµą“ą“³ąµą“ąµ ą“Ŗąµą“°ą“µąµ¼ą“¤ąµą“¤ą“Øą“Ŗą“°ą“æą“ą“ąµą“°ą“ąµą“ą“³ąµą“ąµ ą“ą“æą“² ą“ą“¾ą“ą“ąµą“ąµ¾ ą“øą“®ą“¤ą“¾ą“Ŗąµą“Æą“®ą“¾ą“Æą“¾ą“£ąµ ą“Øą“ą“ąµą“ąµą“Øąµą“Øą“¤ąµ. (ą“ą“¦ą“¾ą“¹ą“°ą“£ą“¤ąµą“¤ą“æą“Øąµ, ą“ą“¾ąµ¼ą“Øąµą“ąµą“ąµ ą“Ŗą“°ą“æą“ą“ąµą“°ą“ ). [1] ą“°ą“¾ą“øą“Ŗąµą“°ą“µąµ¼ą“¤ąµą“¤ą“Øą“ąµą“ą“³ąµą“ąµ ą“¤ą“¾ą“Ŗą“ą“¤ą“æą“ ą“µą“æą“¶ą“ą“²ą“Øą“ąµą“ą“³ą“æąµ½, ą“øą“®ą“¤ą“¾ą“Ŗą“øą“¾ą“¹ą“ą“°ąµą“Æą“ąµą“ą“³ą“æąµ½ ą“ą“Øąµą“¤ą“¾ą“£ąµ ą“øą“ą“ą“µą“æą“ąµą“ąµą“Øąµą“Øą“¤ąµą“Øąµą“Øąµ ą“ą“¦ąµą“Æą“ ą“µą“æą“¶ą“ą“²ą“Øą“ ą“ąµą“Æąµą“Æąµą“ą“Æąµą“ ą“Ŗą“æą“Øąµą“Øąµą“ąµ ą“ ą“¤ą“æąµ½ ą“¤ą“¾ą“Ŗą“Øą“æą“²ą“Æąµą“ąµ ą“Ŗąµą“°ą“ą“¾ą“µą“ ą“Ŗą“°ą“æą“¶ąµą“§ą“æą“ąµą“ąµą“ą“Æąµą“ ą“ąµą“Æąµą“Æą“¾ą“±ąµą“£ąµą“ąµ. [2] , ą“ą“°ąµą“ąµ½ ą“ ą“²ąµą“²ąµą“ąµą“ą“æąµ½ ą“¬ą“¾ą“·ąµą“Ŗąµą“ą“°ą“£ą“ą“ą“Øąµą“Øą“æą“µ ą“Ŗąµą“²ąµą“³ą“³ ą“ ą“µą“øąµą“„ą“¾ą“Øąµą“¤ą“°ą“ąµą“ąµ¾ ą“øą“®ą“¤ą“¾ą“Ŗą“Ŗąµą“°ą“ąµą“°ą“æą“Æą“ą“³ą“¾ą“£ąµ, ą“ ą“µ ą“øąµą“„ą“æą“°ą“®ąµ¼ą“¦ąµą“¦ą“¤ąµą“¤ą“æą“²ą“¾ą“£ąµ ą“øą“ą“ą“µą“æą“ąµą“ąµą“Øąµą“Øą“¤ąµ. [3] ą“ ą“¤ą“æą“øą“ąµą“ąµąµ¼ą“£ą“®ą“¾ą“Æ ą“ ą“øą“®ą“¤ą“¾ą“Ŗą“Ŗąµą“°ą“ąµą“°ą“æą“Æą“ą“³ąµ ą“µą“æą“¶ą“ą“²ą“Øą“ ą“ąµą“Æąµą“Æąµą“Øąµą“Øą“¤ą“æą“Øąµ ą“øą“®ą“¤ą“¾ą“Ŗ ą“Ŗąµą“°ą“ąµą“°ą“æą“Æą“ąµ¾ ą“Ŗą“²ą“Ŗąµą“Ŗąµą““ąµą“ ą“ą“Ŗą“Æąµą“ą“æą“ąµą“ą“¾ą“±ąµą“£ąµą“ąµ. ą“ą“¦ąµ¼ą“¶ ą“µą“¾ą“¤ą“ą“¤ąµą“¤ą“æą“Øąµą“³ąµą“³ ą“µą“æą“¶ą“¦ą“¾ą“ą“¶ą“ąµą“ąµ¾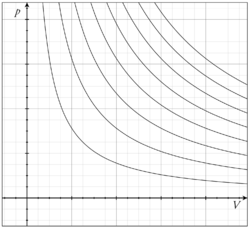 ą“¬ąµą“Æą“²ą“æą“Øąµą“±ąµą“Øą“æą“Æą“®ą“ ą“¬ą“¾ą“§ą“ą“®ą“¾ą“ąµą“Øąµą“Ø ą“ą“°ąµ ą“µą“¾ą“¤ą“ą“¤ąµą“¤ą“æą“Øąµą“±ąµ ą“ą“¾ą“°ąµą“Æą“¤ąµą“¤ą“æąµ½, ą“µą“¾ą“¤ą“ą“ ą“øą“®ą“¤ą“¾ą“Ŗ ą“ ą“µą“øąµą“„ą“Æą“æą“²ą“¾ą“£ąµą“ąµą“ą“æąµ½ ą“®ąµ¼ą“¦ąµą“¦ą“xą“µąµą“Æą“¾ą“Ŗąµą“¤ą“ (pV) ą“ą“°ąµ ą“øąµą“„ą“æą“°ą“¾ą“ąµą“ą“®ą“¾ą“Æą“æą“°ą“æą“ąµą“ąµą“. ą“ ą“øąµą“„ą“æą“°ą“¾ą“ąµą“ą“¤ąµą“¤ą“æą“Øąµą“±ąµ ą“®ąµą“²ąµą“Æą“ nRT ą“ą“£ąµ, ą“ą“µą“æą“ąµ n ą“ą“Øąµą“Øą“¤ąµ ą“µą“¾ą“¤ą“ą“¤ąµą“¤ą“æą“Øąµą“±ąµ ą“®ąµą“³ąµą“ą“³ąµą“ąµ ą“ą“£ąµą“£ą“µąµą“ R ą“ą“¦ąµ¼ą“¶ ą“µą“¾ą“¤ą“ ą“øąµą“„ą“æą“°ą“¾ą“ąµą“ą“µąµą“®ą“¾ą“£ąµ . ą“®ą“±ąµą“±ąµą“°ąµ ą“µą“æą“§ą“¤ąµą“¤ą“æąµ½ ą“Ŗą“±ą“ąµą“ą“¾ąµ½, ą“ą“¦ąµ¼ą“¶ ą“µą“¾ą“¤ą“ ą“Øą“æą“Æą“®ą“ pV= nRT ą“¬ą“¾ą“§ą“ą“®ą“¾ą“£ąµ. ą“ ą“¤ąµą“ąµą“£ąµą“ąµ: ą“ą“ąµą“Øąµą“Øąµ. ą“ ą“øą“®ą“µą“¾ą“ąµą“Æą“ ą“øąµą“·ąµą“ą“æą“ąµą“ąµą“Øąµą“Ø ą“µą“ąµą“°ą“°ąµą“ą“ą“³ąµą“ąµ ą“ą“£ą“ ą“ą“æą“¤ąµą“°ą“ 1 ą“²ąµ ą“ąµą“°ą“¾ą“«ą“æąµ½ ą“ą“¾ą“£ą“æą“ąµą“ą“æą“°ą“æą“ąµą“ąµą“Øąµą“Øąµ. ą“ą“°ąµ ą“µą“ąµą“°ą“¤ąµą“¤ąµą“Æąµą“ ą“øą“®ą“¤ą“¾ą“Ŗą“°ąµą“ (Isotherm) ą“ą“Øąµą“Øąµ ą“µą“æą“³ą“æą“ąµą“ąµą“Øąµą“Øąµ. ą“ ą“¤ąµą“¤ą“°ą“ ą“ąµą“°ą“¾ą“«ąµą“ą“³ąµ ą“ąµ»ą“”ą“æą“ąµą“ąµą“±ąµą“±ąµ¼ ą“”ą“Æą“ąµą“°ą“ ą“ą“Øąµą“Øąµ ą“µą“æą“³ą“æą“ąµą“ąµą“Øąµą“Øąµ, ą“ą“ąµą“ą“æą“Øąµą“ą“³ąµą“ąµ ą“ą“¾ą“°ąµą“Æą“ąµą“·ą“®ą“¤ ą“Øą“æą“°ąµą“ąµą“·ą“æą“ąµą“ąµą“Øąµą“Øą“¤ą“æą“Øąµ ą“ąµą“Æą“æą“ą“øąµ ą“µą“¾ą“ąµą“ąµą“ ą“ąµą“ąµą“ą“°ąµą“ ą“ą“£ąµ ą“ą“¤ąµ ą“ą“¦ąµą“Æą“®ą“¾ą“Æą“æ ą“ą“Ŗą“Æąµą“ą“æą“ąµą“ą“¤ąµ. ą“ą“æą“¤ąµą“°ą“¤ąµą“¤ą“æą“²ąµ ą“ą“°ąµ ą“µą“ąµą“°ą“°ąµą“ą“Æąµą“ąµą“ąµą“ ą“øą“ą“ą“¤ą“®ą“¾ą“Æ ą“¤ą“¾ą“Ŗą“Øą“æą“² ą“¤ą“¾ą““ąµ ą“ą“ą“¤ąµ ą“Øą“æą“Øąµą“Øąµ ą“®ąµą“ą“³ą“æąµ½ ą“µą“²ą“¤ąµą“¤ąµą“ąµą“ąµ ą“µąµ¼ą“¦ąµą“§ą“æą“ąµą“ąµą“Øąµą“Øąµ. ą“²ąµą“ąµ (pĀ¹v1) ą“Ŗąµą“°ą“µąµą“¤ąµą“¤ą“æą“Æąµą“ąµ ą“ą“£ą“ąµą“ąµą“ąµą“ąµą“ąµ½ ą“¤ą“¾ą“Ŗą“ą“¤ą“æą“ą“¤ąµą“¤ą“æąµ½, ą“µą“¾ą“¤ą“ą“ ą“-ą“ ą“µą“øąµą“„ą“Æą“æąµ½ ą“Øą“æą“Øąµą“Øąµ ą“¬ą“æ-ą“ ą“µą“øąµą“„ą“Æą“æą“²ąµą“ąµą“ąµ ą“®ą“¾ą“±ąµą“®ąµą“Ŗąµąµ¾ ą“Ŗąµą“°ą“¤ą“æą“²ąµą“®ąµą“Æ ą“Ŗąµą“°ą“µąµą“¤ąµą“¤ą“æ: [4] ą“ą“¦ąµ¼ą“¶ą“µą“¾ą“¤ą“ą“ąµą“ą“³ąµ ą“øą“ą“¬ą“Øąµą“§ą“æą“ąµą“ą“ą“¤ąµą“¤ąµą“³ą“ ą“ą“°ąµ ą“øą“®ą“¤ą“¾ą“Ŗąµą“Æ, ą“Ŗąµą“°ą“¤ą“æą“²ąµą“®ąµą“Æ ą“Ŗąµą“°ą“ąµą“°ą“æą“Æą“Æą“æąµ½, ą“ ą“ąµ»ąµą“±ą“ąµą“°ąµ½ ą“ ą“¤ą“æą“Øąµą“±ąµ ą“®ąµ¼ą“¦ąµą“¦ą“µąµą“Æą“¾ą“Ŗąµą“¤ą“ąµą“°ą“¾ą“«ą“æą“²ąµ ą“øą“®ą“¤ą“¾ą“Ŗą“°ąµą“ą“Æą“ąµą“ąµ ą“ąµą““ą“æą“²ąµą“³ą“³ ą“µą“æą“øąµą“¤ąµąµ¼ą“£ą“¤ąµą“¤ą“æą“Øąµ ą“¤ąµą“²ąµą“Æą“®ą“¾ą“£ąµ, ą“ą“¤ąµ ą“ą“æą“¤ąµą“°ą“ 2 ąµ½ ą“Ŗąµ¼ą“Ŗąµą“Ŗą“æąµ¾ ą“Øą“æą“±ą“¤ąµą“¤ą“æąµ½ ą“øąµą“ą“æą“Ŗąµą“Ŗą“æą“ąµą“ą“æą“°ą“æą“ąµą“ąµą“Øąµą“Øąµ. ą“ą“¦ąµ¼ą“¶ą“µą“¾ą“¤ą“ą“øą“®ą“µą“¾ą“ąµą“Æą“¤ąµą“¤ą“æąµ½ T ą“øąµą“„ą“æą“°ą“¾ą“ąµą“ą“®ą“¾ą“Æą“¤ą“æą“Øą“¾ąµ½ ą“Ŗąµą“°ą“µąµą“¤ąµą“¤ą“æą“Æąµ ą“ą“Ŗąµą“°ą“ą“¾ą“°ą“ ą“ą““ąµą“¤ą“¾ą“: ą“Ŗąµą“°ą“µąµą“¤ąµą“¤ą“æ ą“ą“Øąµą“Øą“¾ąµ½ ą“øą“¾ą“§ą“¾ą“°ą“£ą“Æą“¾ą“Æą“æ ą“ą“°ąµ ą“µąµą“Æąµą“¹ą“¤ąµą“¤ą“æą“Øąµą“®ąµąµ½ ą“ ą“¤ą“æą“Øąµą“±ąµ ą“ąµą“±ąµą“±ąµą“Ŗą“¾ą“ąµą“ą“³ą“æąµ½ ą“Øą“æą“Øąµą“Øąµą“ ą“ ą“Øąµą“ą“µą“Ŗąµą“Ŗąµą“ąµą“Øąµą“Ø ą“Ŗąµą“°ą“µąµą“¤ąµą“¤ą“æ ą“ą“Øąµą“Øą“¾ą“£ąµ ą“µą“æą“µą“ąµą“·ą“æą“ąµą“ą“Ŗąµą“Ŗąµą“ąµą“Øąµą“Øą“¤ąµ. ą“ą“¦ą“¾ą“¹ą“°ą“£ą“¤ąµą“¤ą“æą“Øąµ, ą“µąµą“Æąµą“¹ą“ ą“øą“®ąµą“®ąµ¼ą“¦ąµą“¦ą“Øą“ ą“ąµą“Æąµą“Æą“Ŗąµą“Ŗąµą“ąµą“ą“¾ąµ½, ą“ ą“Ŗąµą“°ą“µąµą“¤ąµą“¤ą“æ ą“Ŗąµą“øą“æą“±ąµą“±ąµą“µąµ ą“ą“£ąµ, ą“ąµą“ą“¾ą“¤ąµ ą“øą“æą“øąµą“±ąµą“±ą“¤ąµą“¤ą“æą“Øąµą“±ąµ ą“ą“Øąµą“¤ą“°ą“æą“ ą“ąµ¼ą“ąµą“ą“ ą“µąµ¼ą“¦ąµą“§ą“æą“ąµą“ąµą“ą“Æąµą“ ą“ąµą“Æąµą“Æąµą“Øąµą“Øąµ. ą“Øąµą“°ąµą“®ą“±ą“æą“ąµą“ąµ, ą“µąµą“Æąµą“¹ą“ ą“µą“æą“ą“øą“æą“ąµą“ąµą“ą“Æą“¾ą“£ąµą“ąµą“ą“æąµ½, ą“ ą“¤ąµ ą“ąµą“±ąµą“±ąµą“Ŗą“¾ą“ąµą“ą“³ą“æą“²ąµą“Æąµą“ąµą“ąµ ą“ąµą“Æąµą“¤ ą“Ŗąµą“°ą“µąµą“¤ąµą“¤ą“æą“Æą“¾ą“£ąµ. ą“µąµą“Æąµą“¹ą“¤ąµą“¤ą“æą“Øąµą“±ąµ ą“ą“Øąµą“¤ą“°ą“æą“ ą“ąµ¼ą“ąµą“ą“ ą“ąµą“±ą“Æąµą“ą“Æąµą“ ą“ąµą“Æąµą“Æąµą“Øąµą“Øąµ. ą“ą“¦ąµ¼ą“¶ ą“µą“¾ą“¤ą“ą“ąµą“ąµ¾ą“ąµą“ąµ, ą“¤ą“¾ą“Ŗą“Øą“æą“² ą“øąµą“„ą“æą“°ą“®ą“¾ą“Æą“æ ą“Øą“æą“²ą“ąµą“³ąµą“³ąµą“Øąµą“Øąµą“µąµą“ąµą“ą“æąµ½, ą“µąµą“Æąµą“¹ą“¤ąµą“¤ą“æą“Øąµą“±ąµ ą“ą“Øąµą“¤ą“°ą“æą“ ą“ąµ¼ą“ąµą“ą“µąµą“ ą“øąµą“„ą“æą“°ą“®ą“¾ą“Æą“æą“°ą“æą“ąµą“ąµą“, ą“ ą“¤ą“¾ą“Æą“¤ąµ Ī U = 0. ą“ą“Øąµą“Øą“¾ą“ ą“¤ą“¾ą“Ŗą“ą“¤ą“æą“ ą“Øą“æą“Æą“®ą“Ŗąµą“°ą“ą“¾ą“°ą“ U. = Q + W ( IUPAC ą“ąµą““ąµą“µą““ą“ąµą“ą“), ą“ą“Æą“¤ą“æą“Øą“¾ąµ½ ą“ą“¦ąµ¼ą“¶ą“µą“¾ą“¤ą“ą“ąµą“ą“³ąµą“ąµ ą“øą“®ą“¤ą“¾ą“Ŗąµą“Æ ą“øą“®ąµą“®ąµ¼ą“¦ąµą“¦ą“Øą“¤ąµą“¤ą“æą“Øąµą“ ą“µą“æą“ą“¾ą“øą“¤ąµą“¤ą“æą“Øąµą“ Q =-W ą“ą“Øąµą“Ø ą“°ąµą“¤ą“æ ą“Ŗą“æą“Øąµą“¤ąµą“ą“°ąµą“Øąµą“Øąµ. ą“ą“°ąµ ą“øą“®ą“¤ą“¾ą“Ŗą“Ŗąµą“°ą“ąµą“°ą“æą“Æą“Æąµą“ąµ ą“ą“¦ą“¾ą“¹ą“°ą“£ą“ ą“®ą“¾ą“¤ąµą“ą“¾ą“µą“¾ą“¤ą“ą“¤ąµą“¤ą“æą“Øąµą“±ąµ ą“Ŗąµą“°ą“¤ą“æą“²ąµą“®ąµą“Æ ą“µą“æą“ą“¾ą“øą“ ą“®ąµą“²ą“®ąµą“£ąµą“ą“¾ą“ąµą“Øąµą“Ø ą“Ŗąµą“°ą“µąµą“¤ąµą“¤ą“æ ą“øą“®ą“¤ą“¾ą“Ŗą“Ŗąµą“°ą“ąµą“°ą“æą“Æą“®ąµą“ą“¾ą“Øąµą“¤ą“æą“°ą“ ą“ą“£ąµą“ą“¾ą“ąµą“Øąµą“Ø ą“Ŗąµą“°ą“µąµą“¤ąµą“¤ą“æą“ąµą“ąµ ą“ą“¦ą“¾ą“¹ą“°ą“£ą“®ą“¾ą“£ąµ. ą“ą“¤ąµą“ąµą“°ą“®ą“¤ąµą“¤ą“æą“²ąµ ą“®ą“¾ą“±ąµą“±ą“ąµą“ąµ¾ą“ą“¤ąµą“ąµą“°ą“®ą“¤ąµą“¤ą“æą“²ąµ (ą“ąµ»ą“ąµą“°ąµą“Ŗąµą“Ŗą“æ) ą“®ą“¾ą“±ąµą“±ą“ąµą“ąµ¾ ą“ą“£ą“ąµą“ą“¾ą“ąµą“ą“¾ąµ» ą“ą“øąµą“¤ąµąµ¼ą“®ąµ½ ą“Ŗąµą“°ą“ąµą“°ą“æą“Æą“ąµ¾ ą“Ŗąµą“°ą“¤ąµą“Æąµą“ą“æą“ąµą“ąµą“ ą“øąµą“ą“°ąµą“Æą“Ŗąµą“°ą“¦ą“®ą“¾ą“£ąµ, ą“ ą“øą“¾ą“¹ą“ą“°ąµą“Æą“¤ąµą“¤ą“æąµ½, ą“ąµ»ą“ąµą“°ąµą“Ŗąµą“Ŗą“æ ą“®ą“¾ą“±ąµą“±ą“¤ąµą“¤ą“æą“Øąµą“³ąµą“³ ą“øąµą“¤ąµą“°ą“µą“¾ą“ąµą“Æą“ Ī S , ą“ą“µą“æą“ąµ Q rev ą“ą“Øąµą“Øą“¤ąµ ą“øą“æą“øąµą“±ąµą“±ą“¤ąµą“¤ą“æą“²ąµą“ąµą“ąµ ą“Ŗąµą“°ą“¤ą“æą“²ąµą“®ąµą“Æą“®ą“¾ą“Æą“æ ą“ąµą“®ą“¾ą“±ąµą“±ą“ ą“ąµą“Æąµą“Æą“Ŗąµą“Ŗąµą“ąµą“Øąµą“Ø ą“¤ą“¾ą“Ŗą“µąµą“ T ą“ą“Øąµą“Øą“¤ąµ ą“ąµą“µą“² ą“¤ą“¾ą“Ŗą“Øą“æą“²ą“Æąµą“®ą“¾ą“£ąµ . [5] ą“ ą“øąµą“¤ąµą“°ą“µą“¾ą“ąµą“Æą“ ą“ą“°ąµ ą“øą“¾ą“ąµą“ąµ½ą“Ŗąµą“Ŗą“æą“ ą“±ą“æą“µąµąµ¼ą“øą“æą“¬ą“æąµ¾ ą“Ŗąµą“°ą“ąµą“°ą“æą“Æą“Æąµą“ąµą“ąµ ą“®ą“¾ą“¤ąµą“°ą“®ąµ ą“¬ą“¾ą“§ą“ą“®ą“¾ą“ąµ; ą“ ą“¤ą“¾ą“Æą“¤ąµ, ą“ą“²ąµą“²ą“¾ą“Æąµą“Ŗąµą“Ŗąµą““ąµą“ ą“øą“Øąµą“¤ąµą“²ą“æą“¤ą“¾ą“µą“øąµą“„ ą“Øą“æą“²ą“Øą“æąµ¼ą“¤ąµą“¤ąµą“Øąµą“Ø ą“ą“°ąµ ą“Ŗąµą“°ą“ąµą“°ą“æą“Æą“ąµą“ąµ ą“®ą“¾ą“¤ąµą“°ą“. ą“øąµą“„ą“æą“°ą“®ą“¾ą“Æ ą“¤ą“¾ą“Ŗą“Øą“æą“²ą“Æą“æą“²ąµą“ ą“®ąµ¼ą“¦ąµą“¦ą“¤ąµą“¤ą“æą“²ąµą“ ą“Øą“ą“ąµą“ąµą“Øąµą“Ø ą“øą“Øąµą“¤ąµą“²ą“æą“¤ą“®ą“¾ą“Æ ą“ą“°ąµ ą“ ą“µą“øąµą“„ą“¾ą“Øąµą“¤ą“°ą“ (ą“ą“°ąµą“ąµ½ ą“ ą“²ąµą“²ąµą“ąµą“ą“æąµ½ ą“¬ą“¾ą“·ąµą“Ŗąµą“ą“°ą“£ą“ ą“Ŗąµą“²ąµą“³ąµą“³ą“µ) ą“ą“¤ą“æą“Øąµ ą“²ą“³ą“æą“¤ą“®ą“¾ą“Æ ą“ą“°ąµ ą“ą“¦ą“¾ą“¹ą“°ą“£ą“ą“ą“£ąµ. ą“øąµą“„ą“æą“°ą“®ąµ¼ą“¦ąµą“¦ą“¤ąµą“¤ą“æą“²ąµą“³ą“³ ą“ ą“µą“øąµą“„ą“¾ą“Øąµą“¤ą“°ą“ ą“øą“ą“ą“µą“æą“ąµą“ąµą“®ąµą“Ŗąµąµ¾, ą“µąµą“Æąµą“¹ą“¤ąµą“¤ą“æą“²ąµą“ąµą“ąµ ą“ąµą“®ą“¾ą“±ąµą“±ą“ ą“ąµą“Æąµą“Æą“Ŗąµą“Ŗąµą“ąµą“Øąµą“Ø ą“¤ą“¾ą“Ŗą“ ą“Ŗą“°ą“æą“µąµ¼ą“¤ąµą“¤ą“Øą“¤ąµą“¤ą“æą“Øąµą“±ąµ ą“ą“Øąµą“¤ą“¾ąµ½āą“Ŗą“æą“ąµą“ąµ ą“¤ąµą“²ąµą“Æą“®ą“¾ą“£ąµ, Ī H tr, ą“ ą“Ŗąµą“°ą“ą“¾ą“°ą“, Q = Ī H tr . [3] ą“ą“¤ąµą“°ąµ ą“®ąµ¼ą“¦ąµą“¦ą“¤ąµą“¤ą“æą“²ąµą“, ą“°ą“£ąµą“ąµ ą“ ą“µą“øąµą“„ą“ąµ¾ ą“øą“Øąµą“¤ąµą“²ą“Øą“®ą“¾ą“ą“¤ąµą“¤ą“ąµą“ą“µą“æą“§ą“ ą“ą“°ąµ ą“Ŗą“°ą“æą“µąµ¼ą“¤ąµą“¤ą“Ø ą“¤ą“¾ą“Ŗą“Øą“æą“², T tr ą“ą“£ąµą“ą“¾ą“Æą“æą“°ą“æą“ąµą“ąµą“. (ą“ą“¦ą“¾ą“¹ą“°ą“£ą“¤ąµą“¤ą“æą“Øąµ, ą“ą“°ąµ ą“ ą“Øąµą“¤ą“°ąµą“ąµą“·ą“®ąµ¼ą“¦ąµą“¦ą“¤ąµą“¤ą“æąµ½ ą“ą“°ąµ ą“¦ąµą“°ą“¾ą“µą“ą“¤ąµą“¤ąµ ą“¬ą“¾ą“·ąµą“Ŗąµą“ą“°ą“æą“ąµą“ąµą“Øąµą“Øą“¤ą“æą“Øąµą“³ąµą“³ ą“øą“¾ą“§ą“¾ą“°ą“£ ą“¤ą“æą“³ą“Øą“æą“²). ą“ ą“¤ąµą“¤ą“°ą“ ą“øą“Øąµą“¤ąµą“²ą“æą“¤ą“¾ą“µą“øąµą“„ą“Æą“æą“²ą“¾ą“£ąµ ą“Ŗą“°ą“æą“µąµ¼ą“¤ąµą“¤ą“Øą“ ą“Øą“ą“ąµą“ąµą“Øąµą“Øą“¤ąµą“ąµą“ą“æąµ½, ą“ą“¤ąµą“ąµą“°ą“®ą“¤ąµą“¤ą“æą“²ąµ ą“®ą“¾ą“±ąµą“±ą“ ą“Øąµą“°ą“æą“ąµą“ąµ ą“ą“£ą“ąµą“ą“¾ą“ąµą“ą“¾ąµ» ą“®ąµą“ą“³ą“æą“²ąµą“³ąµą“³ ą“øą“®ą“µą“¾ą“ąµą“Æą“ ą“ą“Ŗą“Æąµą“ą“æą“ąµą“ą“¾ą“ [5]
ą“Ŗą“¦ąµąµ½ą“Ŗąµą“Ŗą“¤ąµą“¤ą“æ"ą“ą“øąµą“¤ąµąµ¼ą“®ąµ½" ą“ą“Øąµą“Ø ą“µą“æą“¶ąµą“·ą“£ą“ ą“ąµą“°ąµą“ąµą“ąµ ą“Ŗą“¦ą“ąµą“ą“³ą“¾ą“Æ "į¼“ĻĪæĻ" ("ą“ą“øąµą“øąµ") "ą“¤ąµą“²ąµą“Æą“" ą“ą“Øąµą“Øąµą“ "ą“¤ą“¾ą“Ŗą“" ą“ą“Øąµą“Øąµ¼ą“¤ąµą“„ą“ ą“µą“°ąµą“Øąµą“Ø "Ī·Ī¼Ī·" ("ą“¤ąµąµ¼ą“") ą“ą“Øąµą“Øą“æą“µą“Æą“æąµ½ ą“Øą“æą“Øąµą“Øą“¾ą“£ąµ ą“ą“°ąµą“¤ąµą“¤ą“æą“°ą“æą“ąµą“ą“¤ąµ. ą“ą“¤ąµą“ ą“ą“¾ą“£ąµą“
ą“ ą“µą“²ą“ą“¬ą“
|
Portal di Ensiklopedia Dunia
























