àŽžà”àŽ”à”ŒàŽŁà”àŽŁ àŽ àŽšà”àŽȘàŽŸàŽ€àŽ
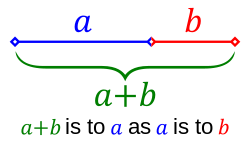 àŽ°àŽŁà”àŽà” àŽžàŽàŽà”àŽŻàŽàŽłà”àŽà” àŽ àŽšà”àŽȘàŽŸàŽ€àŽ àŽ àŽ”àŽŻà”àŽà” àŽ€à”àŽàŽŻà”àŽ àŽàŽŠà”àŽŻàŽ€à”àŽ€à” àŽžàŽàŽà”àŽŻàŽŻà”àŽ àŽ€àŽźà”àŽźàŽżàŽČà”àŽłà”àŽł àŽ àŽšà”àŽȘàŽŸàŽ€àŽ€à”àŽ€àŽżàŽšà”â àŽ€à”àŽČà”àŽŻàŽźàŽŸàŽŁà”àŽà”àŽàŽżà”œ àŽ àŽ” àŽàŽšàŽ àŽ àŽšà”àŽȘàŽŸàŽ€àŽ€à”àŽ€àŽżàŽČàŽŸàŽŁà”àŽšà”àŽšà” (Golden ratio) àŽȘàŽ±àŽŻà”àŽšà”àŽšà”. àŽŹà”àŽàŽàŽŁàŽżàŽ€àŽ°à”àŽȘàŽ€à”àŽ€àŽżà”œ àŽȘà”àŽ°àŽžà”àŽ€àŽŸàŽ”àŽżàŽà”àŽàŽŸà”œ, , àŽàŽšà”àŽšà” àŽ°àŽŁà”àŽà” àŽžàŽàŽà”àŽŻàŽàŽłàŽżà”œ , àŽàŽŁà”àŽà”àŽàŽżà”œ a/b = (a+b)/a = Ï àŽàŽšà”àŽšà”àŽŽà”àŽ€àŽŸàŽ. àŽàŽ”àŽżàŽà” àŽàŽżàŽà”àŽàŽżàŽŻ Ï (àŽ«à”) àŽàŽšà”àŽš àŽà”àŽ°à”àŽà”àŽà” àŽ àŽà”àŽ·àŽ°àŽ àŽžà”àŽàŽżàŽȘà”àŽȘàŽżàŽà”àŽà”àŽšà”àŽš àŽ àŽšà”àŽȘàŽŸàŽ€àŽźàŽŸàŽŁà” àŽàŽšàŽàŽŸàŽšà”àŽȘàŽŸàŽ€àŽ.[1] àŽàŽ€àŽżàŽšà”àŽ±à” àŽ”àŽżàŽČ àŽàŽŁà”â [2]. àŽ àŽ àŽšà”àŽȘàŽŸàŽ€àŽ àŽàŽ°à” àŽ àŽàŽżàŽšà”àŽšàŽàŽźàŽŸàŽŁà”. àŽàŽŁàŽżàŽ€àŽȘàŽ°àŽźàŽŸàŽŻàŽż àŽšàŽżà”ŒàŽŠà”àŽ§àŽŸàŽ°àŽŁàŽ àŽà”àŽŻà”àŽ€àŽŸà”œ àŽàŽ€àŽżàŽšà”àŽ±à” àŽźà”àŽČà”àŽŻàŽ àŽàŽàŽŠà”àŽ¶àŽ 1.618033988749 àŽàŽšà”àŽš àŽžàŽàŽà”àŽŻàŽŻà”àŽà” àŽ àŽà”àŽ€à”àŽ€à”àŽ”àŽ°à”àŽ.[3] àŽȘà”àŽ€à”àŽ€àŽà”àŽ±àŽžà”àŽžà”àŽ àŽ àŽŠà”àŽŠà”àŽčàŽ€à”àŽ€àŽżàŽšà”àŽ±à” àŽ¶àŽżàŽ·à”àŽŻàŽšà”àŽźàŽŸàŽ°à”àŽ àŽȘà”àŽ°àŽ€à”àŽŻà”àŽàŽźàŽŸàŽŻ àŽ àŽ àŽšà”àŽȘàŽŸàŽ€àŽ€à”àŽ€à”àŽà” àŽàŽà”ŒàŽ·àŽżàŽ€àŽ°àŽŸàŽŻàŽżàŽ°à”àŽšà”àŽšà”. àŽȘà”àŽ°àŽ€à”àŽŻà”àŽàŽ€AB àŽ”àŽ¶àŽźàŽŸàŽŻàŽż ABCD àŽàŽšà”àŽš àŽàŽ°à” àŽžàŽźàŽàŽ€à”àŽ°àŽ àŽšàŽżà”ŒàŽźà”àŽźàŽżàŽà”àŽà” AD àŽŻà”àŽà” àŽźàŽŠà”àŽ§à”àŽŻàŽŹàŽżàŽšà”àŽŠà”àŽ”àŽŸàŽŻàŽż E àŽžàŽà”àŽà”œàŽȘà”àŽȘàŽżàŽŻà”àŽà”àŽà”àŽ. EF=EB àŽàŽŻàŽżàŽ°àŽżàŽŻà”àŽà”àŽàŽ€à”àŽ€àŽà”àŽàŽ”àŽŁà”àŽŁàŽ F àŽàŽšà”àŽš àŽŹàŽżàŽšà”àŽŠà” DAà”œ àŽàŽŁà”àŽà”àŽȘàŽżàŽàŽżàŽà”àŽà”, àŽ¶à”àŽ·àŽ AFGP àŽàŽšà”àŽš àŽžàŽźàŽàŽ€à”àŽ°àŽ àŽ”àŽ°àŽà”àŽàŽŸà”œ P,AB àŽŻà” àŽžà”àŽ”à”ŒàŽŁà”àŽŁ àŽ àŽšà”àŽȘàŽŸàŽ€àŽ€à”àŽ€àŽżà”œ àŽ”àŽżàŽàŽàŽżàŽŻà”àŽà”àŽà”àŽ. àŽà”àŽàŽŸàŽ€à”,AB àŽšà”àŽłàŽ”à”àŽ AP àŽ”à”àŽ€àŽżàŽŻà”àŽźà”àŽłà”àŽł àŽàŽ°à” àŽàŽ€à”àŽ°àŽ àŽšàŽżà”ŒàŽźà”àŽźàŽżàŽà”àŽàŽŸà”œ àŽàŽ±à”àŽ±àŽ”à”àŽ àŽźàŽšà”àŽčàŽ°àŽźàŽŸàŽŻ àŽàŽ€à”àŽ°àŽ àŽàŽ€àŽŸàŽŻàŽżàŽ°àŽżàŽŻà”àŽà”àŽà”àŽźàŽ€à”àŽ°à”! àŽ«àŽżàŽŹàŽšàŽŸàŽà”àŽàŽż àŽ¶à”àŽ°à”àŽŁàŽżàŽŻà”àŽ àŽžà”àŽ”à”ŒàŽŁà”àŽŁ àŽ àŽšà”àŽȘàŽŸàŽ€àŽ”à”àŽàŽ àŽà”àŽ€à”àŽ€àŽà”àŽ€à”àŽ€ àŽ°àŽŁà”àŽà” àŽ«àŽżàŽŹàŽšàŽŸàŽà”àŽàŽż àŽžàŽàŽà”àŽŻàŽà”Ÿ àŽ€àŽźà”àŽźàŽżàŽČà”àŽłà”àŽł àŽ àŽšà”àŽȘàŽŸàŽ€àŽ àŽȘàŽ°àŽżàŽ¶à”àŽ§àŽżàŽà”àŽàŽŸà”œ, F2/F1 â 1Ă·1 = 1 F3/F2 â 2Ă·1 = 2 F4/F3 â 3Ă·2 = 1.5 F5/F4 â 5Ă·3 = 1.666.. F6/F5 â 8Ă·5 = 1.6 F7/F6 â 13Ă·8 = 1.625 àŽàŽšà”àŽšàŽżàŽà”àŽàŽšà” àŽàŽżàŽà”àŽà”àŽ. àŽàŽà”àŽàŽšà” àŽ€à”àŽà”ŒàŽšà”àŽšàŽŸà”œ 20-àŽàŽ àŽ«àŽżàŽŹàŽšàŽŸàŽà”àŽàŽż àŽžàŽàŽà”àŽŻàŽŻàŽŸàŽŻ 6765-àŽàŽ 19-àŽàŽ àŽ«àŽżàŽŹàŽšàŽŸàŽà”àŽàŽż àŽžàŽàŽà”àŽŻàŽŻàŽŸàŽŻ 4181-àŽàŽ àŽ€àŽźà”àŽźàŽżàŽČà”àŽłà”àŽł àŽ àŽšà”àŽȘàŽŸàŽ€àŽ 1.618033⊠àŽàŽšà”àŽšà” àŽàŽżàŽà”àŽà”àŽ. F20/F19 â 6765Ă·4181 = 1.618033 àŽ àŽ€àŽŸàŽŻàŽ€à” àŽ«àŽżàŽŹàŽšàŽŸàŽà”àŽàŽż àŽžàŽàŽà”àŽŻ àŽ”àŽČà”àŽ€àŽŸàŽà”àŽàŽ€à”àŽ±à”àŽ àŽ àŽà”àŽ€à”àŽ€àŽà”àŽ€à”àŽ€ àŽ°àŽŁà”àŽà” àŽžàŽàŽà”àŽŻàŽà”Ÿ àŽ€àŽźà”àŽźàŽżàŽČà”àŽłà”àŽł àŽ àŽšà”àŽȘàŽŸàŽ€àŽ àŽžà”àŽ”à”ŒàŽŁà”àŽŁàŽŸàŽšà”àŽȘàŽŸàŽ€àŽźàŽŸàŽŻàŽż àŽźàŽŸàŽ±à”àŽšà”àŽšàŽ€àŽŸàŽŻàŽż àŽàŽŸàŽŁàŽŸàŽ.[4] àŽ àŽ”àŽČàŽàŽŹàŽ
|
Portal di Ensiklopedia Dunia

















