–í–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ–į—Ź –ľ–ĺ–∑–į–ł–ļ–į –Ņ–ĺ—Ä—Ź–ī–ļ–į 4
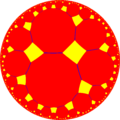
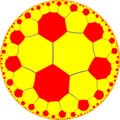
–í–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ–į—Ź –ľ–ĺ–∑–į–ł–ļ–į –Ņ–ĺ—Ä—Ź–ī–ļ–į 4 ‚ÄĒ —ć—ā–ĺ –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–į—Ź –ľ–ĺ–∑–į–ł–ļ–į –Ĺ–į –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł .
–ú–ĺ–∑–į–ł–ļ–į –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–į —Ā–ł–ľ–≤–ĺ–Ľ–ĺ–ľ –®–Ľ–Ķ—Ą–Ľ–ł {8,4}.
–ē—Ď —ą–į—Ö–ľ–į—ā–Ĺ–į—Ź —Ä–į—Ā–ļ—Ä–į—Ā–ļ–į –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ĺ–į–∑–≤–į–Ĺ–į –≤–ĺ—Ā—Ć–ľ–ł-–≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–Ļ –ľ–ĺ–∑–į–ł–ļ–ĺ–Ļ –ł –Ķ—Ď —Ā–ľ–≤–ĺ–Ľ –®–Ľ–Ķ—Ą–Ľ–ł r{8,8}.
–ė–ľ–Ķ–Ķ—ā—Ā—Ź —á–Ķ—ā—č—Ä–Ķ –ĺ–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ—č—Ö –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź —ć—ā–ĺ–Ļ –ľ–ĺ–∑–į–ł–ļ–ł. –Ę—Ä–ł –ł–∑ –Ĺ–ł—Ö –ĺ—Ā—É—Č–Ķ—Ā—ā–≤–Ľ—Ź—é—ā—Ā—Ź —É–ī–į–Ľ–Ķ–Ĺ–ł–Ķ–ľ –∑–Ķ—Ä–ļ–į–Ľ–į –ł–∑ –ļ–į–Ľ–Ķ–Ļ–ī–ĺ—Ā–ļ–ĺ–Ņ–į [8,8] .
–£–ī–į–Ľ–Ķ–Ĺ–ł–Ķ –∑–Ķ—Ä–ļ–į–Ľ–į –ľ–Ķ–∂–ī—É —ā–ĺ—á–ļ–į–ľ–ł –Ņ–ĺ—Ä—Ź–ī–ļ–į 2 –ł 4 –ī–į—Ď—ā [8,8,1+ ] —Ā —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ķ–Ļ [(8,8,4)] (*884) [–į–Ĺ–≥–Ľ.] *4444 .
–ß–Ķ—ā—č—Ä–Ķ –ĺ–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ—č—Ö –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź 8.8.8.8
–ě–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ–į—Ź
–°–ł–ľ–ľ–Ķ—ā—Ä–ł—Ź [–į–Ĺ–≥–Ľ.] [8,4]
[8,8]
[(8,4,8)] = [8,8,1+ ]
[1+ ,8,8,1+ ]
–°–ł–ľ–≤–ĺ–Ľ
{8,4}
r{8,8}
r(8,4,8) = r{8,8}1 ‚ĀĄ2
r{8,4}1 ‚ĀĄ8 1 ‚ĀĄ4
–Ē–ł–į–≥—Ä–į–ľ–ľ–į
–≠—ā–į –ľ–ĺ–∑–į–ł–ļ–į –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–ł—á–Ķ—Ā–ļ–ł–Ļ –ļ–į–Ľ–Ķ–Ļ–ī–ĺ—Ā–ļ–ĺ–Ņ –ł–∑ 8 –∑–Ķ—Ä–ļ–į–Ľ, –Ĺ–į—Ö–ĺ–ī—Ź—Č–ł—Ö—Ā—Ź –Ĺ–į –ļ—Ä–į—Ź—Ö –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ą–Ķ—Ā—ā–ł—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į.
–≠—ā–į —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—Ź –≤ –ĺ—Ä–Ī–ł—Ą–ĺ–Ľ–ī–Ĺ–ĺ–Ļ –Ĺ–ĺ—ā–į—Ü–ł–ł [–į–Ĺ–≥–Ľ.] 8 ) —Ā 8 –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź–ľ–ł –∑–Ķ—Ä–ļ–į–Ľ –Ņ–ĺ—Ä—Ź–ī–ļ–į 2.
–í –Ĺ–ĺ—ā–į—Ü–ł–ł –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä [–į–Ĺ–≥–Ľ.] * ,4],
–ļ–ĺ—ā–ĺ—Ä–į—Ź –Ņ–ĺ–Ľ—É—á–į–Ķ—ā—Ā—Ź —É–ī–į–Ľ–Ķ–Ĺ–ł–Ķ–ľ –ī–≤—É—Ö –∑–Ķ—Ä–ļ–į–Ľ (–Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–ł—Ö —á–Ķ—Ä–Ķp–Ķ–∑ —Ü–Ķ–Ĺ—ā—Ä –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į) –≤ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł [8,4].
–Ē–ĺ–Ī–į–≤–Ľ–Ķ–Ĺ–ł–Ķ –∑–Ķ—Ä–ļ–į–Ľ–į, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–Ķ–≥–ĺ —á–Ķ—Ä–Ķ–∑ 2 –≤–Ķ—Ä—ą–ł–Ĺ—č –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ—Ć–Ĺ–ĺ–Ļ –ĺ–Ī–Ľ–į—Ā—ā–ł –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā —ā—Ä–į–Ņ–Ķ—Ü–ĺ—ć–ī—Ä–į–Ľ—Ć–Ĺ—É—é —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—é *4422 .
–Ē–ĺ–Ī–į–≤–Ľ–Ķ–Ĺ–ł–Ķ 4 –∑–Ķ—Ä–ļ–į–Ľ, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–ł—Ö —á–Ķ—Ä–Ķ–∑ –≤–Ķ—Ä—ą–ł–Ĺ—č, –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—é *444 .
–Ē–ĺ–Ī–į–≤–Ľ–Ķ–Ĺ–ł–Ķ 4 –∑–Ķ—Ä–ļ–į–Ľ, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–ł—Ö —á–Ķ—Ä–Ķ–∑ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č, –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—é *4222 [–į–Ĺ–≥–Ľ.] —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł *842 .
–§—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ—Ć–Ĺ—É—é –ĺ–Ī–Ľ–į—Ā—ā—Ć –ļ–į–Ľ–Ķ–Ļ–ī–ĺ—Ā–ļ–ĺ–Ņ–į –ľ–ĺ–∂–Ĺ–ĺ —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—ā—Ć –ļ–į–ļ –ī–≤—É—Ö—Ü–≤–Ķ—ā–Ĺ—É—é –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—É—é –ľ–ĺ–∑–į–ł–ļ—É,
–Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—é—Č—É—é –∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ—č–Ķ –ĺ–Ī—Ä–į–∑—č —Ą—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ—Ć–Ĺ–ĺ–Ļ –ĺ–Ī–Ľ–į—Ā—ā–ł.
–≠—ā–į —Ä–į—Ā–ļ—Ä–į—Ā–ļ–į –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā –ĺ–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ—É—é –ļ–≤–į–∑–ł–Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ—É—é –ľ–ĺ–∑–į–ł–ļ—É r{8,8}, –ļ–ĺ—ā–ĺ—Ä—É—é –ľ–ĺ–∂–Ĺ–ĺ –Ĺ–į–∑–≤–į—ā—Ć –≤–ĺ—Ā—Ć–ľ–ł-–≤–ĺ—Ā—Ć–ľ–ł–≥–ĺ–Ĺ–į–Ľ—Ć–Ĺ–ĺ–Ļ –ľ–ĺ–∑–į–ł–ļ–ĺ–Ļ .
–≠—ā–į –ľ–ĺ–∑–į–ł–ļ–į —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —á–į—Ā—ā—Ć—é –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ—č—Ö –ľ–ĺ–∑–į–ł–ļ —Ā –≤–ĺ—Ā–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–ľ–ł –≥—Ä–į–Ĺ—Ź–ľ–ł.
–ü–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā—Ć –Ĺ–į—á–ł–Ĺ–į–Ķ—ā—Ā—Ź —Ā –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–Ļ –ľ–ĺ–∑–į–ł–ļ–ł , –ł–ľ–Ķ—é—Č–Ķ–Ļ —Ā–ł–ľ–≤–ĺ–Ľ –®–Ľ–Ķ—Ą–Ľ–ł {8,n} –ł
–ī–ł–į–≥—Ä–į–ľ–ľ—É –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į
–í–į—Ä–ł–į–Ĺ—ā—č —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł *n 42 –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ—č—Ö –ľ–ĺ–∑–į–ł–ļ {n ,4}
–°—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ
–ē–≤–ļ–Ľ–ł–ī–ĺ–≤—č
–ď–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–ł—á–Ķ—Ā–ļ–ł–Ķ –ľ–ĺ–∑–į–ł–ļ–ł
24
34
44
54
64
74
84
...‚ąě4
–≠—ā–į –ľ–ĺ–∑–į–ł–ļ–į —ā–į–ļ–∂–Ķ —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —á–į—Ā—ā—Ć—é –Ņ–ĺ—Ā–Ľ–Ķ–ī–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ—č—Ö –ľ–Ĺ–ĺ–≥–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–ĺ–≤ –ł –ľ–ĺ–∑–į–ł–ļ —Ā —á–Ķ—ā—č—Ä—Ć–ľ—Ź –≥—Ä–į–Ĺ—Ź–ľ–ł –≤ –≤–Ķ—Ä—ą–ł–Ĺ–Ķ.
–ü–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā—Ć –Ĺ–į—á–ł–Ĺ–į–Ķ—ā—Ā —Ā –ĺ–ļ—ā–į—ć–ī—Ä–į , –ł–ľ–Ķ–Ķ—ā —Ā–ł–ľ–≤–ĺ–Ľ –®–Ľ–Ķ—Ą–Ľ–ł {n,4} –ł –ī–ł–į–≥—Ä–į–ľ–ľ—É –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į
–ě–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ—č–Ķ –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ/–ļ–≤–į–ī—Ä–į—ā–Ĺ—č–Ķ –ľ–ĺ–∑–į–ł–ļ–ł
[8,4], (*842)
{8,4}
t{8,4} r{8,4}
2t{8,4}=t{4,8}
2r{8,4}={4,8}
rr{8,4}
tr{8,4}
–ě–ī–Ĺ–ĺ—Ä–ī–Ĺ—č–Ķ –ī–≤–ĺ–Ļ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ
V84
V4.16.16
V(4.8)2
V8.8.8
V48
V4.4.4.8
V4.8.16
–ź–Ľ—Ć—ā–Ķ—Ä–Ĺ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č–Ķ
[1+ ,8,4]
[8+ ,4]
[8,1+ ,4]
[8,4+ ]
[8,4,1+ ]
[(8,4,2+ )]
[8,4]+
h{8,4}
s{8,4}
hr{8,4}
s{4,8}
h{4,8}
hrr{8,4}
sr{8,4}
–ź–Ľ—Ć—ā–Ķ—Ä–Ĺ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č–Ķ –ī–≤–ĺ–Ļ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ
V(4.4)4
V3.(3.8)2
V(4.4.4)2
V(3.4)3
V88
V4.44
V3.3.4.3.8
–ě–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ—č–Ķ –≤–ĺ—Ā—Ć–ľ–ł–≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ –ľ–ĺ–∑–į–ł–ļ–ł
–°–ł–ľ–ľ–Ķ—ā—Ä–ł—Ź: [8,8], (*882)
{8,8}
t{8,8} r{8,8}
2t{8,8}=t{8,8}
2r{8,8}={8,8}
rr{8,8}
tr{8,8}
–ě–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ—č–Ķ –ī–≤–ĺ–Ļ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ
V88
V8.16.16
V8.8.8.8
V8.16.16
V88
V4.8.4.8
V4.16.16
–ź–Ľ—Ć—ā–Ķ—Ä–Ĺ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č–Ķ
[1+ ,8,8]
[8+ ,8]
[8,1+ ,8]
[8,8+ ]
[8,8,1+ ]
[(8,8,2+ )]
[8,8]+
h{8,8}
s{8,8}
hr{8,8}
s{8,8}
h{8,8}
hrr{8,8}
sr{8,8}
–ź–Ľ—Ć—ā–Ķ—Ä–Ĺ–į—ā–ł–≤–Ĺ—č–Ķ –ī–≤–ĺ–Ļ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ
V(4.8)8
V3.4.3.8.3.8
V(4.4)4
V3.4.3.8.3.8
V(4.8)8
V46
V3.3.8.3.8
John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss.Chapter 19 The Hyperbolic Archimedean Tessellations) // The Symmetries of Things . ‚ÄĒ 2008. ‚ÄĒ ISBN 978-1-56881-220-5 .Chapter 10: Regular honeycombs in hyperbolic space // The Beauty of Geometry: Twelve Essays. ‚ÄĒ Dover Publications, 1999. ‚ÄĒ ISBN 0-486-40919-8 .