–ó–į–ī–į—á–į –ĺ –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–ľ –Ņ–ĺ—ā–ĺ–ļ–Ķ 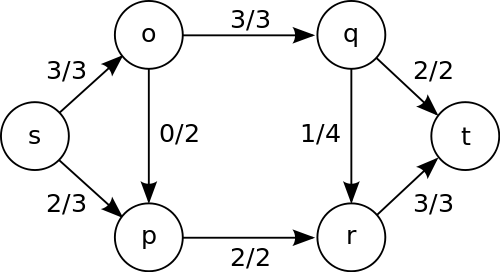 –ú–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ—č–Ļ –Ņ–ĺ—ā–ĺ–ļ –≤ —ā—Ä–į–Ĺ—Ā–Ņ–ĺ—Ä—ā–Ĺ–ĺ–Ļ —Ā–Ķ—ā–ł. –ß–ł—Ā–Ľ–į –ĺ–Ī–ĺ–∑–Ĺ–į—á–į—é—ā –Ņ–ĺ—ā–ĺ–ļ–ł –ł –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ—č–Ķ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā–ł. –ú–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ—č–Ļ –Ņ–ĺ—ā–ĺ–ļ –≤ —ā—Ä–į–Ĺ—Ā–Ņ–ĺ—Ä—ā–Ĺ–ĺ–Ļ —Ā–Ķ—ā–ł. –ß–ł—Ā–Ľ–į –ĺ–Ī–ĺ–∑–Ĺ–į—á–į—é—ā –Ņ–ĺ—ā–ĺ–ļ–ł –ł –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ—č–Ķ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā–ł.
–í —ā–Ķ–ĺ—Ä–ł–ł –ĺ–Ņ—ā–ł–ľ–ł–∑–į—Ü–ł–ł –ł —ā–Ķ–ĺ—Ä–ł–ł –≥—Ä–į—Ą–ĺ–≤, –∑–į–ī–į—á–į –ĺ –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–ľ –Ņ–ĺ—ā–ĺ–ļ–Ķ –∑–į–ļ–Ľ—é—á–į–Ķ—ā—Ā—Ź –≤ –Ĺ–į—Ö–ĺ–∂–ī–Ķ–Ĺ–ł–ł —ā–į–ļ–ĺ–≥–ĺ –Ņ–ĺ—ā–ĺ–ļ–į –Ņ–ĺ —ā—Ä–į–Ĺ—Ā–Ņ–ĺ—Ä—ā–Ĺ–ĺ–Ļ —Ā–Ķ—ā–ł, —á—ā–ĺ —Ā—É–ľ–ľ–į –Ņ–ĺ—ā–ĺ–ļ–ĺ–≤ –ł–∑ –ł—Ā—ā–ĺ–ļ–į, –ł–Ľ–ł, —á—ā–ĺ —ā–ĺ –∂–Ķ —Ā–į–ľ–ĺ–Ķ, —Ā—É–ľ–ľ–į –Ņ–ĺ—ā–ĺ–ļ–ĺ–≤ –≤ —Ā—ā–ĺ–ļ –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–į.
–ó–į–ī–į—á–į –ĺ –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–ľ –Ņ–ĺ—ā–ĺ–ļ–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —á–į—Ā—ā–Ĺ—č–ľ —Ā–Ľ—É—á–į–Ķ–ľ –Ī–ĺ–Ľ–Ķ–Ķ —ā—Ä—É–ī–Ĺ—č—Ö –∑–į–ī–į—á, –ļ–į–ļ –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä –∑–į–ī–į—á–į –ĺ —Ü–ł—Ä–ļ—É–Ľ—Ź—Ü–ł–ł.
–ė—Ā—ā–ĺ—Ä–ł—Ź
–ü–ĺ—Ā–Ľ–Ķ –≤—Ā—ā—É–Ņ–Ľ–Ķ–Ĺ–ł—Ź –°–®–ź –≤–ĺ –í—ā–ĺ—Ä—É—é –ľ–ł—Ä–ĺ–≤—É—é –≤–ĺ–Ļ–Ĺ—É –≤ 1941 –≥–ĺ–ī—É –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ –Ē–∂–ĺ—Ä–ī–∂ –Ď–Ķ—Ä–Ĺ–į—Ä–ī –Ē–į–Ĺ—Ü–ł–≥ –Ņ–ĺ—Ā—ā—É–Ņ–ł–Ľ –Ĺ–į —Ä–į–Ī–ĺ—ā—É –≤ –ĺ—ā–ī–Ķ–Ľ —Ā—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —É–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł—Ź –í–ĺ–Ķ–Ĺ–Ĺ–ĺ-–≤–ĺ–∑–ī—É—ą–Ĺ—č—Ö —Ā–ł–Ľ –°–®–ź –≤ –í–į—ą–ł–Ĺ–≥—ā–ĺ–Ĺ–Ķ. –° 1941 –Ņ–ĺ 1946 –≥–ĺ–ī—č –ĺ–Ĺ –≤–ĺ–∑–≥–Ľ–į–≤–Ľ—Ź–Ľ –Ņ–ĺ–ī—Ä–į–∑–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ –į–Ĺ–į–Ľ–ł–∑–į –Ī–ĺ–Ķ–≤—č—Ö –ī–Ķ–Ļ—Ā—ā–≤–ł–Ļ (Combat Analysis Branch), –≥–ī–Ķ —Ä–į–Ī–ĺ—ā–į–Ľ –Ĺ–į–ī —Ä–į–∑–Ľ–ł—á–Ĺ—č–ľ–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł–ľ–ł –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–į–ľ–ł.[1][2] –í–Ņ–ĺ—Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–ł c –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ–ľ —Ä–į–Ī–ĺ—ā—č –Ē–į–Ĺ—Ü–ł–≥–į –∑–į–ī–į—á–į –ĺ –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–ľ –Ņ–ĺ—ā–ĺ–ļ–Ķ –Ī—č–Ľ–į –≤–Ņ–Ķ—Ä–≤—č–Ķ —Ä–Ķ—ą–Ķ–Ĺ–į –≤ —Ö–ĺ–ī–Ķ –Ņ–ĺ–ī–≥–ĺ—ā–ĺ–≤–ļ–ł –≤–ĺ–∑–ī—É—ą–Ĺ–ĺ–≥–ĺ –ľ–ĺ—Ā—ā–į –≤–ĺ –≤—Ä–Ķ–ľ—Ź –Ī–Ľ–ĺ–ļ–į–ī—č –ó–į–Ņ–į–ī–Ĺ–ĺ–≥–ĺ –Ď–Ķ—Ä–Ľ–ł–Ĺ–į, –Ņ—Ä–ĺ–ł—Ā—Ö–ĺ–ī–ł–≤—ą–Ķ–Ļ –≤ 1948‚ÄĒ1949 –≥–ĺ–ī—É.[3][4][5]
–í 1951 –≥–ĺ–ī—É –Ē–∂–ĺ—Ä–ī–∂ –Ē–į–Ĺ—Ü–ł–≥ –≤–Ņ–Ķ—Ä–≤—č–Ķ —Ā—Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–į–Ľ –∑–į–ī–į—á—É –≤ –ĺ–Ī—Č–Ķ–ľ –≤–ł–ī–Ķ.[6]
–í 1955 –≥–ĺ–ī—É, –õ–Ķ—Ā—ā–Ķ—Ä –§–ĺ—Ä–ī –ł –Ē–Ķ–Ľ–Ī–Ķ—Ä—ā –§–į–Ľ–ļ–Ķ—Ä—Ā–ĺ–Ĺ (–į–Ĺ–≥–Ľ. Delbert Ray Fulkerson) –≤–Ņ–Ķ—Ä–≤—č–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–ł–Ľ–ł –į–Ľ–≥–ĺ—Ä–ł—ā–ľ, —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ–ĺ –Ņ—Ä–Ķ–ī–Ĺ–į–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—č–Ļ –ī–Ľ—Ź —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź —ć—ā–ĺ–Ļ –∑–į–ī–į—á–ł. –ė—Ö –į–Ľ–≥–ĺ—Ä–ł—ā–ľ –Ņ–ĺ–Ľ—É—á–ł–Ľ –Ĺ–į–∑–≤–į–Ĺ–ł–Ķ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ –§–ĺ—Ä–ī–į-–§–į–Ľ–ļ–Ķ—Ä—Ā–ĺ–Ĺ–į.[7][8]
–í –ī–į–Ľ—Ć–Ĺ–Ķ–Ļ—ą–Ķ–ľ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ –∑–į–ī–į—á–ł –ľ–Ĺ–ĺ–≥–ĺ —Ä–į–∑ —É–Ľ—É—á—ą–į–Ľ–ĺ—Ā—Ć.
–í 2010 –≥–ĺ–ī—É –ł—Ā—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł –Ē–∂–ĺ–Ĺ–į—ā–į–Ĺ –ö—Ď–Ľ–Ĺ–Ķ—Ä (Jonathan Kelner) –ł –ź–Ľ–Ķ–ļ—Ā–į–Ĺ–ī–Ķ—Ä –ú–ĺ–Ĺ–ī—Ä—č (Aleksander MńÖdry) –ł–∑ –ú–Ę–ė –≤–ľ–Ķ—Ā—ā–Ķ —Ā–ĺ —Ā–≤–ĺ–ł–ľ–ł –ļ–ĺ–Ľ–Ľ–Ķ–≥–į–ľ–ł –Ē—ć–Ĺ–ł–Ķ–Ľ–Ķ–ľ –°–Ņ–ł–Ľ–ľ–Ķ–Ĺ–ĺ–ľ –ł–∑ –ô–Ķ–Ľ—Ć—Ā–ļ–ĺ–≥–ĺ —É–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į –ł –Ę—ć–Ĺ–ĺ–ľ –®–į–Ĺ—Ö—É–į –ł–∑ –ģ–∂–Ĺ–ĺ-–ö–į–Ľ–ł—Ą–ĺ—Ä–Ĺ–ł–Ļ—Ā–ļ–ĺ–≥–ĺ —É–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į –Ņ—Ä–ĺ–ī–Ķ–ľ–ĺ–Ĺ—Ā—ā—Ä–ł—Ä–ĺ–≤–į–Ľ–ł –ĺ—á–Ķ—Ä–Ķ–ī–Ĺ–ĺ–Ķ —É–Ľ—É—á—ą–Ķ–Ĺ–ł–Ķ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–į, –≤–Ņ–Ķ—Ä–≤—č–Ķ –∑–į 10 –Ľ–Ķ—ā.[3][9][10]
–ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ
–Ē–į–Ĺ–į —ā—Ä–į–Ĺ—Ā–Ņ–ĺ—Ä—ā–Ĺ–į—Ź —Ā–Ķ—ā—Ć  —Ā –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–ĺ–ľ —Ā –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–ĺ–ľ  , —Ā—ā–ĺ–ļ–ĺ–ľ , —Ā—ā–ĺ–ļ–ĺ–ľ  –ł –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ—č–ľ–ł —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā—Ź–ľ–ł –ł –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ—č–ľ–ł —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā—Ź–ľ–ł  . .
- –í–Ķ–Ľ–ł—á–ł–Ĺ–ĺ–Ļ –Ņ–ĺ—ā–ĺ–ļ–į (value of flow) –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź —Ā—É–ľ–ľ–į –Ņ–ĺ—ā–ĺ–ļ–ĺ–≤ –ł–∑ –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–į
 . –í —Ā—ā–į—ā—Ć–Ķ ¬ę–Ę—Ä–į–Ĺ—Ā–Ņ–ĺ—Ä—ā–Ĺ–į—Ź —Ā–Ķ—ā—ƬĽ –ī–ĺ–ļ–į–∑–į–Ĺ–ĺ, —á—ā–ĺ –ĺ–Ĺ–į —Ä–į–≤–Ĺ–į —Ā—É–ľ–ľ–Ķ –Ņ–ĺ—ā–ĺ–ļ–ĺ–≤ –≤ —Ā—ā–ĺ–ļ . –í —Ā—ā–į—ā—Ć–Ķ ¬ę–Ę—Ä–į–Ĺ—Ā–Ņ–ĺ—Ä—ā–Ĺ–į—Ź —Ā–Ķ—ā—ƬĽ –ī–ĺ–ļ–į–∑–į–Ĺ–ĺ, —á—ā–ĺ –ĺ–Ĺ–į —Ä–į–≤–Ĺ–į —Ā—É–ľ–ľ–Ķ –Ņ–ĺ—ā–ĺ–ļ–ĺ–≤ –≤ —Ā—ā–ĺ–ļ  . .
–ó–į–ī–į—á–į –ĺ –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–ľ –Ņ–ĺ—ā–ĺ–ļ–Ķ –∑–į–ļ–Ľ—é—á–į–Ķ—ā—Ā—Ź –≤ –Ĺ–į—Ö–ĺ–∂–ī–Ķ–Ĺ–ł–ł —ā–į–ļ–ĺ–≥–ĺ –Ņ–ĺ—ā–ĺ–ļ–į, –≥–ī–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ–į –Ņ–ĺ—ā–ĺ–ļ–į –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–į.
–†–Ķ—ą–Ķ–Ĺ–ł—Ź
–°–Ľ–Ķ–ī—É—é—Č–į—Ź —ā–į–Ī–Ľ–ł—Ü–į –Ņ–Ķ—Ä–Ķ—á–ł—Ā–Ľ—Ź–Ķ—ā –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—č–Ķ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ—č —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –∑–į–ī–į—á–ł.
| –ú–Ķ—ā–ĺ–ī
|
–°–Ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć
|
–ě–Ņ–ł—Ā–į–Ĺ–ł–Ķ
|
| –õ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ–≥—Ä–į–ľ–ľ–ł—Ä–ĺ–≤–į–Ĺ–ł–Ķ
|
–ó–į–≤–ł—Ā–ł—ā –ĺ—ā –ļ–ĺ–Ĺ–ļ—Ä–Ķ—ā–Ĺ–ĺ–≥–ĺ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–į. –Ē–Ľ—Ź —Ā–ł–ľ–Ņ–Ľ–Ķ–ļ—Ā-–ľ–Ķ—ā–ĺ–ī–į —ć–ļ—Ā–Ņ–ĺ–Ĺ–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ–į.
|
–ü—Ä–Ķ–ī—Ā—ā–į–≤–ł—ā—Ć –∑–į–ī–į—á—É –ĺ –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–ľ –Ņ–ĺ—ā–ĺ–ļ–Ķ –ļ–į–ļ –∑–į–ī–į—á—É –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ–≥—Ä–į–ľ–ľ–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź. –ü–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č–ľ–ł —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –Ņ–ĺ—ā–ĺ–ļ–ł –Ņ–ĺ —Ä—Ď–Ī—Ä–į–ľ, –į –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ł—Ź–ľ–ł ‚ÄĒ —Ā–ĺ—Ö—Ä–į–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ–ĺ—ā–ĺ–ļ–į –ł –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ–ĺ–Ļ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā–ł.
|
| –ź–Ľ–≥–ĺ—Ä–ł—ā–ľ –§–ĺ—Ä–ī–į-–§–į–Ľ–ļ–Ķ—Ä—Ā–ĺ–Ĺ–į
|
–ó–į–≤–ł—Ā–ł—ā –ĺ—ā –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–į –Ņ–ĺ–ł—Ā–ļ–į —É–≤–Ķ–Ľ–ł—á–ł–≤–į—é—Č–Ķ–≥–ĺ –Ņ—É—ā–ł. –Ę—Ä–Ķ–Ī—É–Ķ—ā  —ā–į–ļ–ł—Ö –Ņ–ĺ–ł—Ā–ļ–ĺ–≤. —ā–į–ļ–ł—Ö –Ņ–ĺ–ł—Ā–ļ–ĺ–≤.
|
–Ě–į–Ļ—ā–ł –Ľ—é–Ī–ĺ–Ļ —É–≤–Ķ–Ľ–ł—á–ł–≤–į—é—Č–ł–Ļ –Ņ—É—ā—Ć. –£–≤–Ķ–Ľ–ł—á–ł—ā—Ć –Ņ–ĺ—ā–ĺ–ļ –Ņ–ĺ –≤—Ā–Ķ–ľ –Ķ–≥–ĺ —Ä—Ď–Ī—Ä–į–ľ –Ĺ–į –ľ–ł–Ĺ–ł–ľ–į–Ľ—Ć–Ĺ—É—é –ł–∑ –ł—Ö –ĺ—Ā—ā–į—ā–ĺ—á–Ĺ—č—Ö –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ—č—Ö —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā–Ķ–Ļ. –ü–ĺ–≤—ā–ĺ—Ä—Ź—ā—Ć, –Ņ–ĺ–ļ–į —É–≤–Ķ–Ľ–ł—á–ł–≤–į—é—Č–ł–Ļ –Ņ—É—ā—Ć –Ķ—Ā—ā—Ć. –ź–Ľ–≥–ĺ—Ä–ł—ā–ľ —Ä–į–Ī–ĺ—ā–į–Ķ—ā —ā–ĺ–Ľ—Ć–ļ–ĺ –ī–Ľ—Ź —Ü–Ķ–Ľ—č—Ö –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ—č—Ö —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā–Ķ–Ļ. –í –Ņ—Ä–ĺ—ā–ł–≤–Ĺ–ĺ–ľ —Ā–Ľ—É—á–į–Ķ –ĺ–Ĺ –ľ–ĺ–∂–Ķ—ā —Ä–į–Ī–ĺ—ā–į—ā—Ć –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ –ī–ĺ–Ľ–≥–ĺ, –Ĺ–Ķ —Ā—Ö–ĺ–ī—Ź—Ā—Ć –ļ –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–ľ—É –ĺ—ā–≤–Ķ—ā—É.
|
| –ź–Ľ–≥–ĺ—Ä–ł—ā–ľ –≠–ī–ľ–ĺ–Ĺ–ī—Ā–į-–ö–į—Ä–Ņ–į
|

|
–í—č–Ņ–ĺ–Ľ–Ĺ—Ź–Ķ–ľ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ –§–ĺ—Ä–ī–į-–§–į–Ľ–ļ–Ķ—Ä—Ā–ĺ–Ĺ–į, –ļ–į–∂–ī—č–Ļ —Ä–į–∑ –≤—č–Ī–ł—Ä–į—Ź –ļ—Ä–į—ā—á–į–Ļ—ą–ł–Ļ —É–≤–Ķ–Ľ–ł—á–ł–≤–į—é—Č–ł–Ļ –Ņ—É—ā—Ć (–Ĺ–į—Ö–ĺ–ī–ł—ā—Ā—Ź –Ņ–ĺ–ł—Ā–ļ–ĺ–ľ –≤ —ą–ł—Ä–ł–Ĺ—É).
|
| –ź–Ľ–≥–ĺ—Ä–ł—ā–ľ –Ē–ł–Ĺ–ł—Ü–į
|
 –ł–Ľ–ł –ł–Ľ–ł  –ī–Ľ—Ź –Ķ–ī–ł–Ĺ–ł—á–Ĺ—č—Ö –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ—č—Ö —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā–Ķ–Ļ –ī–Ľ—Ź –Ķ–ī–ł–Ĺ–ł—á–Ĺ—č—Ö –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ—č—Ö —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā–Ķ–Ļ  —Ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ–ľ –ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ł—Ö –ī–Ķ—Ä–Ķ–≤—Ć–Ķ–≤ –°–Ľ–Ķ—ā–ĺ—Ä–į –ł –Ę–į—Ä—Ć—Ź–Ĺ–į[11] —Ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ–ľ –ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ł—Ö –ī–Ķ—Ä–Ķ–≤—Ć–Ķ–≤ –°–Ľ–Ķ—ā–ĺ—Ä–į –ł –Ę–į—Ä—Ć—Ź–Ĺ–į[11]
|
–£—Ā–ĺ–≤–Ķ—Ä—ą–Ķ–Ĺ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł–Ķ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–į –≠–ī–ľ–ĺ–Ĺ–ī—Ā–į-–ö–į—Ä–Ņ–į (–Ĺ–ĺ —Ö—Ä–ĺ–Ĺ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł –Ī—č–Ľ –Ĺ–į–Ļ–ī–Ķ–Ĺ —Ä–į–Ĺ—Ć—ą–Ķ). –Ě–į –ļ–į–∂–ī–ĺ–Ļ –ł—ā–Ķ—Ä–į—Ü–ł–ł, –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź –Ņ–ĺ–ł—Ā–ļ –≤ —ą–ł—Ä–ł–Ĺ—É, –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ–ľ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –ĺ—ā –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–į –ī–ĺ –≤—Ā–Ķ—Ö –≤–Ķ—Ä—ą–ł–Ĺ –≤ –ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ–Ļ —Ā–Ķ—ā–ł. –°—ā—Ä–ĺ–ł–ľ –≥—Ä–į—Ą, —Ā–ĺ–ī–Ķ—Ä–∂–į—Č–ł–Ļ —ā–ĺ–Ľ—Ć–ļ–ĺ —ā–į–ļ–ł–Ķ —Ä—Ď–Ī—Ä–į –ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ–Ļ —Ā–Ķ—ā–ł, –Ĺ–į –ļ–ĺ—ā–ĺ—Ä—č—Ö —ć—ā–ĺ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ —Ä–į—Ā—ā—Ď—ā –Ĺ–į 1. –ė—Ā–ļ–Ľ—é—á–į–Ķ–ľ –ł–∑ –≥—Ä–į—Ą–į –≤—Ā–Ķ —ā—É–Ņ–ł–ļ–ĺ–≤—č–Ķ –≤–Ķ—Ä—ą–ł–Ĺ—č —Ā –ł–Ĺ—Ü–ł–ī–Ķ–Ĺ—ā–Ĺ—č–ľ–ł –ł–ľ —Ä—Ď–Ī—Ä–į–ľ–ł, –Ņ–ĺ–ļ–į –≤—Ā–Ķ –≤–Ķ—Ä—ą–ł–Ĺ—č –Ĺ–Ķ —Ā—ā–į–Ĺ—É—ā –Ĺ–Ķ—ā—É–Ņ–ł–ļ–ĺ–≤—č–ľ–ł. (–Ę—É–Ņ–ł–ļ–ĺ–≤–ĺ–Ļ –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –≤–Ķ—Ä—ą–ł–Ĺ–į, –ļ—Ä–ĺ–ľ–Ķ –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–į –ł —Ā—ā–ĺ–ļ–į, –≤ –ļ–ĺ—ā–ĺ—Ä—É—é –Ĺ–Ķ –≤—Ö–ĺ–ī–ł—ā –Ĺ–ł –ĺ–ī–Ĺ–ĺ —Ä–Ķ–Ī—Ä–ĺ –ł–Ľ–ł –ł–∑ –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –Ĺ–Ķ –ł—Ā—Ö–ĺ–ī–ł—ā –Ĺ–ł –ĺ–ī–Ĺ–ĺ–≥–ĺ —Ä–Ķ–Ī—Ä–į.) –Ě–į –Ņ–ĺ–Ľ—É—á–ł–≤—ą–Ķ–ľ—Ā—Ź –≥—Ä–į—Ą–Ķ –ĺ—ā—č—Ā–ļ–ł–≤–į–Ķ–ľ –ļ—Ä–į—ā—á–į–Ļ—ą–ł–Ļ —É–≤–Ķ–Ľ–ł—á–ł–≤–į—é—Č–ł–Ļ –Ņ—É—ā—Ć (–ł–ľ –Ī—É–ī–Ķ—ā –Ľ—é–Ī–ĺ–Ļ –Ņ—É—ā—Ć –ł–∑ s –≤ t). –ė—Ā–ļ–Ľ—é—á–į–Ķ–ľ –ł–∑ –ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ–Ļ —Ā–Ķ—ā–ł —Ä–Ķ–Ī—Ä–ĺ —Ā –ľ–ł–Ĺ–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ–ĺ–Ļ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā—Ć—é, —Ā–Ĺ–ĺ–≤–į –ł—Ā–ļ–Ľ—é—á–į–Ķ–ľ —ā—É–Ņ–ł–ļ–ĺ–≤—č–Ķ –≤–Ķ—Ä—ą–ł–Ĺ—č, –ł —ā–į–ļ –Ņ–ĺ–ļ–į —É–≤–Ķ–Ľ–ł—á–ł–≤–į—é—Č–ł–Ļ –Ņ—É—ā—Ć –Ķ—Ā—ā—Ć.
|
| –ź–Ľ–≥–ĺ—Ä–ł—ā–ľ –Ņ—Ä–ĺ—ā–į–Ľ–ļ–ł–≤–į–Ĺ–ł—Ź –Ņ—Ä–Ķ–ī–Ņ–ĺ—ā–ĺ–ļ–į
|

|
–í–ľ–Ķ—Ā—ā–ĺ –Ņ–ĺ—ā–ĺ–ļ–į –ĺ–Ņ–Ķ—Ä–ł—Ä—É–Ķ—ā —Ā –Ņ—Ä–Ķ–ī–Ņ–ĺ—ā–ĺ–ļ–ĺ–ľ. –ě—ā–Ľ–ł—á–ł–Ķ –≤ —ā–ĺ–ľ, —á—ā–ĺ –ī–Ľ—Ź –Ľ—é–Ī–ĺ–Ļ –≤–Ķ—Ä—ą–ł–Ĺ—č u, –ļ—Ä–ĺ–ľ–Ķ –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–į –ł —Ā—ā–ĺ–ļ–į, —Ā—É–ľ–ľ–į –≤—Ö–ĺ–ī—Ź—Č–ł—Ö –≤ –Ĺ–Ķ—Ď –Ņ–ĺ—ā–ĺ–ļ–ĺ–≤ –ī–Ľ—Ź –Ņ–ĺ—ā–ĺ–ļ–į –ī–ĺ–Ľ–∂–Ĺ–į –Ī—č—ā—Ć —Ā—ā—Ä–ĺ–≥–ĺ –Ĺ—É–Ľ–Ķ–≤–ĺ–Ļ (—É—Ā–Ľ–ĺ–≤–ł–Ķ —Ā–ĺ—Ö—Ä–į–Ĺ–Ķ–Ĺ–ł—Ź –Ņ–ĺ—ā–ĺ–ļ–į), –į –ī–Ľ—Ź –Ņ—Ä–Ķ–ī–Ņ–ĺ—ā–ĺ–ļ–į ‚ÄĒ –Ĺ–Ķ–ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ. –≠—ā–į —Ā—É–ľ–ľ–į –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –ł–∑–Ī—č—ā–ĺ—á–Ĺ—č–ľ –Ņ–ĺ—ā–ĺ–ļ–ĺ–ľ –≤ –≤–Ķ—Ä—ą–ł–Ĺ—É, –į –≤–Ķ—Ä—ą–ł–Ĺ–į —Ā –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ –ł–∑–Ī—č—ā–ĺ—á–Ĺ—č–ľ –Ņ–ĺ—ā–ĺ–ļ–ĺ–ľ –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –Ņ–Ķ—Ä–Ķ–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–Ĺ–ĺ–Ļ. –ö—Ä–ĺ–ľ–Ķ —ā–ĺ–≥–ĺ, –ī–Ľ—Ź –ļ–į–∂–ī–ĺ–Ļ –≤–Ķ—Ä—ą–ł–Ĺ—č –į–Ľ–≥–ĺ—Ä–ł—ā–ľ —Ā–ĺ—Ö—Ä–į–Ĺ—Ź–Ķ—ā –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ—É—é —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł–ļ—É, –≤—č—Ā–ĺ—ā—É, —Ź–≤–Ľ—Ź—é—Č—É—é—Ā—Ź —Ü–Ķ–Ľ—č–ľ –Ĺ–Ķ–ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–ľ —á–ł—Ā–Ľ–ĺ–ľ. –ź–Ľ–≥–ĺ—Ä–ł—ā–ľ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā –ī–≤–Ķ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł: –Ņ—Ä–ĺ—ā–į–Ľ–ļ–ł–≤–į–Ĺ–ł–Ķ, –ļ–ĺ–≥–ī–į –Ņ–ĺ—ā–ĺ–ļ –Ņ–ĺ —Ä–Ķ–Ī—Ä—É, –ł–ī—É—Č–Ķ–ľ—É –ł–∑ –Ī–ĺ–Ľ–Ķ–Ķ –≤—č—Ā–ĺ–ļ–ĺ–Ļ –≤ –Ī–ĺ–Ľ–Ķ–Ķ –Ĺ–ł–∑–ļ—É—é –≤–Ķ—Ä—ą–ł–Ĺ—É, —É–≤–Ķ–Ľ–ł—á–ł–≤–į–Ķ—ā—Ā—Ź –Ĺ–į –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ—É—é –≤–Ķ–Ľ–ł—á–ł–Ĺ—É, –ł –Ņ–ĺ–ī—ä—Ď–ľ, –ļ–ĺ–≥–ī–į –Ņ–Ķ—Ä–Ķ–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–Ĺ–į—Ź –≤–Ķ—Ä—ą–ł–Ĺ–į, –Ņ—Ä–ĺ—ā–į–Ľ–ļ–ł–≤–į–Ĺ–ł–Ķ –ł–∑ –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –Ĺ–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ –ł–∑-–∑–į –Ĺ–Ķ–ī–ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ–Ļ –≤—č—Ā–ĺ—ā—č, –Ņ–ĺ–ī–Ĺ–ł–ľ–į–Ķ—ā—Ā—Ź. –ü—Ä–ĺ—ā–į–Ľ–ļ–ł–≤–į–Ĺ–ł–Ķ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ, –ļ–ĺ–≥–ī–į —Ä–Ķ–Ī—Ä–ĺ –Ņ—Ä–ł–Ĺ–į–ī–Ľ–Ķ–∂–ł—ā –ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ–Ļ —Ā–Ķ—ā–ł, –≤–Ķ–ī—Ď—ā –ł–∑ –Ī–ĺ–Ľ–Ķ–Ķ –≤—č—Ā–ĺ–ļ–ĺ–Ļ –≤–Ķ—Ä—ą–ł–Ĺ—č –≤ –Ī–ĺ–Ľ–Ķ–Ķ –Ĺ–ł–∑–ļ—É—é, –ł –ł—Ā—Ö–ĺ–ī–Ĺ–į—Ź –≤–Ķ—Ä—ą–ł–Ĺ–į –Ņ–Ķ—Ä–Ķ–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–į. –ü–ĺ–ī—ä—Ď–ľ –≤–ĺ–∑–ľ–ĺ–∂–Ķ–Ĺ, –ļ–ĺ–≥–ī–į –Ņ–ĺ–ī–Ĺ–ł–ľ–į–Ķ–ľ–į—Ź –≤–Ķ—Ä—ą–ł–Ĺ–į –Ņ–Ķ—Ä–Ķ–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–į, –Ĺ–ĺ –Ĺ–ł –ĺ–ī–Ĺ–į –ł–∑ –≤–Ķ—Ä—ą–ł–Ĺ, –≤ –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ł–∑ –Ĺ–Ķ—Ď –≤–Ķ–ī—É—ā —Ä—Ď–Ī—Ä–į –ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ–Ļ —Ā–Ķ—ā–ł, –Ĺ–Ķ –Ĺ–ł–∂–Ķ –Ķ—Ď. –ě–Ĺ —Ā–ĺ–≤–Ķ—Ä—ą–į–Ķ—ā—Ā—Ź –ī–ĺ –≤—č—Ā–ĺ—ā—č –Ĺ–į 1 –Ī–ĺ–Ľ—Ć—ą–Ķ–Ļ, —á–Ķ–ľ –ľ–ł–Ĺ–ł–ľ–į–Ľ—Ć–Ĺ–į—Ź –ł–∑ –≤—č—Ā–ĺ—ā —ć—ā–ł—Ö –≤–Ķ—Ä—ą–ł–Ĺ. –ė–∑–Ĺ–į—á–į–Ľ—Ć–Ĺ–ĺ –≤—č—Ā–ĺ—ā–į –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–į V, –Ņ–ĺ –≤—Ā–Ķ–ľ —Ä—Ď–Ī—Ä–į–ľ, –ł—Ā—Ö–ĺ–ī—Ź—Č–ł–ľ –ł–∑ –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–į, —ā–Ķ—á—Ď—ā –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ—č–Ļ –Ņ–ĺ—ā–ĺ–ļ, –į –ĺ—Ā—ā–į–Ľ—Ć–Ĺ—č–Ķ –≤—č—Ā–ĺ—ā—č –ł –Ņ–ĺ—ā–ĺ–ļ–ł –Ĺ—É–Ľ–Ķ–≤—č–Ķ. –ě–Ņ–Ķ—Ä–į—Ü–ł–ł –Ņ—Ä–ĺ—ā–į–Ľ–ļ–ł–≤–į–Ĺ–ł—Ź –ł –Ņ–ĺ–ī—ä—Ď–ľ–į –≤—č–Ņ–ĺ–Ľ–Ĺ—Ź—é—ā—Ā—Ź –ī–ĺ —ā–Ķ—Ö –Ņ–ĺ—Ä, –Ņ–ĺ–ļ–į —ć—ā–ĺ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ.
|
| –ź–Ľ–≥–ĺ—Ä–ł—ā–ľ ¬ę–Ņ–ĺ–ī–Ĺ—Ź—ā—Ć –≤ –Ĺ–į—á–į–Ľ–嬼
|
 –ł–Ľ–ł –ł–Ľ–ł  —Ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ–ľ –ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ł—Ö –ī–Ķ—Ä–Ķ–≤—Ć–Ķ–≤ —Ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ–ľ –ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ł—Ö –ī–Ķ—Ä–Ķ–≤—Ć–Ķ–≤
|
–í–į—Ä–ł–į–Ĺ—ā –Ņ—Ä–Ķ–ī—č–ī—É—Č–Ķ–≥–ĺ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–į, —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ—č–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—é—Č–ł–Ļ –Ņ–ĺ—Ä—Ź–ī–ĺ–ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–Ļ –Ņ—Ä–ĺ—ā–į–Ľ–ļ–ł–≤–į–Ĺ–ł—Ź –ł –Ņ–ĺ–ī—ä—Ď–ľ–į.
|
| –ź–Ľ–≥–ĺ—Ä–ł—ā–ľ –ī–≤–ĺ–ł—á–Ĺ–ĺ–≥–ĺ –Ī–Ľ–ĺ–ļ–ł—Ä—É—é—Č–Ķ–≥–ĺ –Ņ–ĺ—ā–ĺ–ļ–į [1]
|

|
–Ē–Ľ—Ź –Ī–ĺ–Ľ–Ķ–Ķ –Ņ–ĺ–ī—Ä–ĺ–Ī–Ĺ–ĺ–≥–ĺ —Ā–Ņ–ł—Ā–ļ–į, —Ā–ľ. [2] –ł –°–Ņ–ł—Ā–ĺ–ļ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–ĺ–≤ –Ĺ–į—Ö–ĺ–∂–ī–Ķ–Ĺ–ł—Ź –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –Ņ–ĺ—ā–ĺ–ļ–į.
–Ę–Ķ–ĺ—Ä–Ķ–ľ–į –ĺ —Ü–Ķ–Ľ–ĺ–ľ –Ņ–ĺ—ā–ĺ–ļ–Ķ
–ē—Ā–Ľ–ł –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ—č–Ķ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā–ł —Ü–Ķ–Ľ—č–Ķ, –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–į—Ź –≤–Ķ–Ľ–ł—á–ł–Ĺ–į –Ņ–ĺ—ā–ĺ–ļ–į —ā–ĺ–∂–Ķ —Ü–Ķ–Ľ–į—Ź.
–Ę–Ķ–ĺ—Ä–Ķ–ľ–į —Ā–Ľ–Ķ–ī—É–Ķ—ā, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, –ł–∑ —ā–Ķ–ĺ—Ä–Ķ–ľ—č –§–ĺ—Ä–ī–į‚ÄĒ–§–į–Ľ–ļ–Ķ—Ä—Ā–ĺ–Ĺ–į.
–ě–Ī–ĺ–Ī—Č–Ķ–Ĺ–ł—Ź, —Ā–≤–ĺ–ī—Ź—Č–ł–Ķ—Ā—Ź –ļ –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–Ļ –∑–į–ī–į—á–Ķ
–Ě–Ķ–ļ–ĺ—ā–ĺ—Ä—č–Ķ –ĺ–Ī–ĺ–Ī—Č–Ķ–Ĺ–ł—Ź –∑–į–ī–į—á–ł –ĺ –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–ľ –Ņ–ĺ—ā–ĺ–ļ–Ķ –Ľ–Ķ–≥–ļ–ĺ —Ā–≤–ĺ–ī—Ź—ā—Ā—Ź –ļ –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–Ļ –∑–į–ī–į—á–Ķ.
–ü—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–ĺ–≤ –ł/–ł–Ľ–ł —Ā—ā–ĺ–ļ–ĺ–≤
–ē—Ā–Ľ–ł –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–ĺ–≤ –Ī–ĺ–Ľ—Ć—ą–Ķ –ĺ–ī–Ĺ–ĺ–≥–ĺ, –ī–ĺ–Ī–į–≤–Ľ—Ź–Ķ–ľ –Ĺ–ĺ–≤—É—é –≤–Ķ—Ä—ą–ł–Ĺ—É S, –ļ–ĺ—ā–ĺ—Ä—É—é –ī–Ķ–Ľ–į–Ķ–ľ –Ķ–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–ľ –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–ĺ–ľ. –Ē–ĺ–Ī–į–≤–Ľ—Ź–Ķ–ľ —Ä—Ď–Ī—Ä–į —Ā –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–Ļ –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ–ĺ–Ļ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā—Ć—é –ĺ—ā S –ļ –ļ–į–∂–ī–ĺ–ľ—É –ł–∑ —Ā—ā–į—Ä—č—Ö –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–ĺ–≤.
–ź–Ĺ–į–Ľ–ĺ–≥–ł—á–Ĺ–ĺ, –Ķ—Ā–Ľ–ł —Ā—ā–ĺ–ļ–ĺ–≤ –Ī–ĺ–Ľ—Ć—ą–Ķ –ĺ–ī–Ĺ–ĺ–≥–ĺ, –ī–ĺ–Ī–į–≤–Ľ—Ź–Ķ–ľ –Ĺ–ĺ–≤—É—é –≤–Ķ—Ä—ą–ł–Ĺ—É T, –ļ–ĺ—ā–ĺ—Ä—É—é –ī–Ķ–Ľ–į–Ķ–ľ –Ķ–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–ľ —Ā—ā–ĺ–ļ–ĺ–ľ. –Ē–ĺ–Ī–į–≤–Ľ—Ź–Ķ–ľ —Ä—Ď–Ī—Ä–į —Ā –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–Ļ –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ–ĺ–Ļ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā—Ć—é –ĺ—ā –ļ–į–∂–ī–ĺ–≥–ĺ –ł–∑ —Ā—ā–į—Ä—č—Ö —Ā—ā–ĺ–ļ–ĺ–≤ –ļ T.
–Ě–Ķ–ĺ—Ä–ł–Ķ–Ĺ—ā–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č–Ķ —Ä—Ď–Ī—Ä–į
–ö–į–∂–ī–ĺ–Ķ –Ĺ–Ķ–ĺ—Ä–ł–Ķ–Ĺ—ā–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ķ —Ä–Ķ–Ī—Ä–ĺ (u, v) –∑–į–ľ–Ķ–Ĺ—Ź–Ķ–ľ –Ĺ–į –Ņ–į—Ä—É –ĺ—Ä–ł–Ķ–Ĺ—ā–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č—Ö —Ä—Ď–Ī–Ķ—Ä (u, v) –ł (v, u).
–ě–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ–ĺ–Ļ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā–ł –≤–Ķ—Ä—ą–ł–Ĺ
–ö–į–∂–ī—É—é –≤–Ķ—Ä—ą–ł–Ĺ—É v —Ā –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–Ĺ–ĺ–Ļ –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ–ĺ–Ļ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā—Ć—é  —Ä–į—Ā—Č–Ķ–Ņ–Ľ—Ź–Ķ–ľ –Ĺ–į –ī–≤–Ķ –≤–Ķ—Ä—ą–ł–Ĺ—č vin –ł vout. –í—Ā–Ķ —Ä—Ď–Ī—Ä–į, –ī–ĺ —Ä–į—Ā—Č–Ķ–Ņ–Ľ–Ķ–Ĺ–ł—Ź –≤—Ö–ĺ–ī—Ź—Č–ł–Ķ –≤ v, —ā–Ķ–Ņ–Ķ—Ä—Ć –≤—Ö–ĺ–ī—Ź—ā –≤ vin. –í—Ā–Ķ —Ä—Ď–Ī—Ä–į, –ī–ĺ —Ä–į—Ā—Č–Ķ–Ņ–Ľ–Ķ–Ĺ–ł—Ź –ł—Ā—Ö–ĺ–ī—Ź—Č–ł–Ķ –ł–∑ v, —ā–Ķ–Ņ–Ķ—Ä—Ć –ł—Ā—Ö–ĺ–ī—Ź—ā –ł–∑ vout. –Ē–ĺ–Ī–į–≤–Ľ—Ź–Ķ–ľ —Ä–Ķ–Ī—Ä–ĺ (vin,vout) —Ā –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ–ĺ–Ļ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā—Ć—é —Ä–į—Ā—Č–Ķ–Ņ–Ľ—Ź–Ķ–ľ –Ĺ–į –ī–≤–Ķ –≤–Ķ—Ä—ą–ł–Ĺ—č vin –ł vout. –í—Ā–Ķ —Ä—Ď–Ī—Ä–į, –ī–ĺ —Ä–į—Ā—Č–Ķ–Ņ–Ľ–Ķ–Ĺ–ł—Ź –≤—Ö–ĺ–ī—Ź—Č–ł–Ķ –≤ v, —ā–Ķ–Ņ–Ķ—Ä—Ć –≤—Ö–ĺ–ī—Ź—ā –≤ vin. –í—Ā–Ķ —Ä—Ď–Ī—Ä–į, –ī–ĺ —Ä–į—Ā—Č–Ķ–Ņ–Ľ–Ķ–Ĺ–ł—Ź –ł—Ā—Ö–ĺ–ī—Ź—Č–ł–Ķ –ł–∑ v, —ā–Ķ–Ņ–Ķ—Ä—Ć –ł—Ā—Ö–ĺ–ī—Ź—ā –ł–∑ vout. –Ē–ĺ–Ī–į–≤–Ľ—Ź–Ķ–ľ —Ä–Ķ–Ī—Ä–ĺ (vin,vout) —Ā –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ–ĺ–Ļ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā—Ć—é  . .
–ě–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ–ĺ–Ļ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā–ł —Ä—Ď–Ī–Ķ—Ä —Ā–Ĺ–ł–∑—É
–í –ī–į–Ĺ–Ĺ–ĺ–ľ –≤–į—Ä–ł–į–Ĺ—ā–Ķ –Ņ–ĺ—Ā—ā–į–Ĺ–ĺ–≤–ļ–ł –∑–į–ī–į—á–ł –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –Ņ–ĺ—ā–ĺ–ļ–į –ļ–į–∂–ī–ĺ–≥–ĺ —Ä–Ķ–Ī—Ä–į –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ĺ —Ā–Ĺ–ł–∑—É —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ  . –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ –≤–Ķ–Ľ–ł—á–ł–Ĺ–į –Ņ–ĺ—ā–ĺ–ļ–į –ī–Ľ—Ź –Ľ—é–Ī–ĺ–≥–ĺ —Ä–Ķ–Ī—Ä–į –Ĺ–Ķ –ľ–ĺ–∂–Ķ—ā –Ņ—Ä–Ķ–≤—č—Ā–ł—ā—Ć –Ķ–≥–ĺ –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ—É—é —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā—Ć, –Ĺ–ĺ –ł –Ĺ–Ķ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –ľ–Ķ–Ĺ—Ć—ą–Ķ –∑–į–ī–į–Ĺ–Ĺ–ĺ–≥–ĺ –ľ–ł–Ĺ–ł–ľ—É–ľ–į, —ā.–Ķ. . –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ –≤–Ķ–Ľ–ł—á–ł–Ĺ–į –Ņ–ĺ—ā–ĺ–ļ–į –ī–Ľ—Ź –Ľ—é–Ī–ĺ–≥–ĺ —Ä–Ķ–Ī—Ä–į –Ĺ–Ķ –ľ–ĺ–∂–Ķ—ā –Ņ—Ä–Ķ–≤—č—Ā–ł—ā—Ć –Ķ–≥–ĺ –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ—É—é —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā—Ć, –Ĺ–ĺ –ł –Ĺ–Ķ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –ľ–Ķ–Ĺ—Ć—ą–Ķ –∑–į–ī–į–Ĺ–Ĺ–ĺ–≥–ĺ –ľ–ł–Ĺ–ł–ľ—É–ľ–į, —ā.–Ķ.  . –Ē–Ľ—Ź —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –∑–į–ī–į—á–ł –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į—ā—Ć –ł—Ā—Ö–ĺ–ī–Ĺ—É—é —ā—Ä–į–Ĺ—Ā–Ņ–ĺ—Ä—ā–Ĺ—É—é —Ā–Ķ—ā—Ć . –Ē–Ľ—Ź —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –∑–į–ī–į—á–ł –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į—ā—Ć –ł—Ā—Ö–ĺ–ī–Ĺ—É—é —ā—Ä–į–Ĺ—Ā–Ņ–ĺ—Ä—ā–Ĺ—É—é —Ā–Ķ—ā—Ć  –≤ —ā—Ä–į–Ĺ—Ā–Ņ–ĺ—Ä—ā–Ĺ—É—é —Ā–Ķ—ā—Ć –≤ —ā—Ä–į–Ĺ—Ā–Ņ–ĺ—Ä—ā–Ĺ—É—é —Ā–Ķ—ā—Ć  —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ: —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ:
- –Ē–ĺ–Ī–į–≤—Ć –Ĺ–ĺ–≤—č–Ķ –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ
 –ł —Ā—ā–ĺ–ļ –ł —Ā—ā–ĺ–ļ  . .
- –Ē–Ľ—Ź –ļ–į–∂–ī–ĺ–≥–ĺ —Ä–Ķ–Ī—Ä–į
 : :
- –°–ĺ–∑–ī–į–Ļ –ī–≤–Ķ –Ĺ–ĺ–≤—č–Ķ –≤–Ķ—Ä—ą–ł–Ĺ—č
 –ł –ł  . .
- –£—Ā—ā–į–Ĺ–ĺ–≤–ł
 –ł –ł  . .
- –£—Ā—ā–į–Ĺ–ĺ–≤–ł
 . .
- –£—Ā—ā–į–Ĺ–ĺ–≤–ł
 –ł –ł  . .
- –£—Ā—ā–į–Ĺ–ĺ–≤–ł
 . .
–í  –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ –Ņ–ĺ—ā–ĺ–ļ, —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź—é—Č–ł–Ļ —É—Ā–Ľ–ĺ–≤–ł—é –ĺ–Ī –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ł–ł –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ–ĺ–Ļ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā–ł —Ä–Ķ–Ī—Ď—Ä —Ā–Ĺ–ł–∑—É, —ā–ĺ–≥–ī–į –ł —ā–ĺ–Ľ—Ć–ļ–ĺ —ā–ĺ–≥–ī–į, –ļ–ĺ–≥–ī–į –≤ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ –Ņ–ĺ—ā–ĺ–ļ, —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź—é—Č–ł–Ļ —É—Ā–Ľ–ĺ–≤–ł—é –ĺ–Ī –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ł–ł –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ–ĺ–Ļ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā–ł —Ä–Ķ–Ī—Ď—Ä —Ā–Ĺ–ł–∑—É, —ā–ĺ–≥–ī–į –ł —ā–ĺ–Ľ—Ć–ļ–ĺ —ā–ĺ–≥–ī–į, –ļ–ĺ–≥–ī–į –≤  –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ—č–Ļ –Ņ–ĺ—ā–ĺ–ļ, –≤ –ļ–ĺ—ā–ĺ—Ä–ĺ–ľ –≤—Ā–Ķ —Ä—Ď–Ī—Ä–į –≤–ł–ī–į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ—č–Ļ –Ņ–ĺ—ā–ĺ–ļ, –≤ –ļ–ĺ—ā–ĺ—Ä–ĺ–ľ –≤—Ā–Ķ —Ä—Ď–Ī—Ä–į –≤–ł–ī–į  –ł –ł  "–Ĺ–į—Ā—č—Č–Ķ–Ĺ—č". –Ď–Ľ–į–≥–ĺ–ī–į—Ä—Ź —ā–į–ļ–ĺ–ľ—É –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—é –į–Ľ–≥–ĺ—Ä–ł—ā–ľ –Ĺ–į—Ö–ĺ–∂–ī–Ķ–Ĺ–ł—Ź –Ņ–ĺ—ā–ĺ–ļ–į, –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —Ā–Ĺ–ł–∑—É –Ī—É–ī–Ķ—ā —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ: "–Ĺ–į—Ā—č—Č–Ķ–Ĺ—č". –Ď–Ľ–į–≥–ĺ–ī–į—Ä—Ź —ā–į–ļ–ĺ–ľ—É –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—é –į–Ľ–≥–ĺ—Ä–ł—ā–ľ –Ĺ–į—Ö–ĺ–∂–ī–Ķ–Ĺ–ł—Ź –Ņ–ĺ—ā–ĺ–ļ–į, –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —Ā–Ĺ–ł–∑—É –Ī—É–ī–Ķ—ā —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ:
- –ė–∑
 –Ņ–ĺ—Ā—ā—Ä–ĺ–Ļ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ļ  . .
- –Ě–į–Ļ–ī–ł –Ņ–ĺ—ā–ĺ–ļ
 –≥—Ä–į—Ą–į –≥—Ä–į—Ą–į  , –Ņ—Ä–Ķ–ī–Ņ–ĺ—á–ł—ā–į—Ź —Ä—Ď–Ī—Ä–į –≤–ł–ī–į , –Ņ—Ä–Ķ–ī–Ņ–ĺ—á–ł—ā–į—Ź —Ä—Ď–Ī—Ä–į –≤–ł–ī–į  –ł –ł  . .
- –ē—Ā–Ľ–ł
 , –≥–ī–Ķ , –≥–ī–Ķ  - –Ņ–ĺ—ā–ĺ–ļ –≥—Ä–į—Ą–į - –Ņ–ĺ—ā–ĺ–ļ –≥—Ä–į—Ą–į  , –≤ –ļ–ĺ—ā–ĺ—Ä–ĺ–ľ –ĺ–Ņ—É—Č–Ķ–Ĺ–į –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ–į—Ź —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā—Ć —Ä—Ď–Ī–Ķ—Ä —Ā–Ĺ–ł–∑—É, —ā–ĺ —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –Ĺ–Ķ —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā. , –≤ –ļ–ĺ—ā–ĺ—Ä–ĺ–ľ –ĺ–Ņ—É—Č–Ķ–Ĺ–į –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ–į—Ź —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā—Ć —Ä—Ď–Ī–Ķ—Ä —Ā–Ĺ–ł–∑—É, —ā–ĺ —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –Ĺ–Ķ —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā.
- –ė–Ĺ–į—á–Ķ –≤—č—á–ł—Ā–Ľ–ł –Ņ–ĺ—ā–ĺ–ļ
 –ł–∑ –Ņ–ĺ—ā–ĺ–ļ–į –ł–∑ –Ņ–ĺ—ā–ĺ–ļ–į  , —ā.–Ķ. , —ā.–Ķ.  . .
–ě–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–Ĺ–ĺ–Ļ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā–ł —Ä—Ď–Ī–Ķ—Ä —Ā–Ĺ–ł–∑—É —Ā –į–Ľ—Ć—ā–Ķ—Ä–Ĺ–į—ā–ł–≤–ĺ–Ļ
–Ę–į–ļ–ĺ–Ļ –≤–į—Ä–ł–į–Ĺ—ā –∑–į–ī–į—á–ł –ł–ī–Ķ–Ĺ—ā–ł—á–Ķ–Ĺ –Ņ—Ä–Ķ–ī—č–ī—É—Č–Ķ–ľ—É —Ā —ā–ĺ–Ļ —Ä–į–∑–Ĺ–ł—Ü–Ķ–Ļ, —á—ā–ĺ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –Ņ–ĺ—ā–ĺ–ļ–į –ī–Ľ—Ź –ļ–į–∂–ī–ĺ–≥–ĺ —Ä–Ķ–Ī—Ä–į –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć —ā–į–ļ–∂–Ķ —Ä–į–≤–Ĺ–ĺ  , —ā.–Ķ. , —ā.–Ķ.  –ł–Ľ–ł –ł–Ľ–ł  . –Ě–Ķ—Ā–ľ–ĺ—ā—Ä—Ź –Ĺ–į –Ĺ–Ķ–∑–Ĺ–į—á–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ķ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ —É—Ā–Ľ–ĺ–≤–ł—Ź, –Ĺ–Ķ —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ–ł–Ĺ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –ī–į–Ĺ–Ĺ–ĺ–Ļ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ—č, –Ķ—Ā–Ľ–ł –ļ–Ľ–į—Ā—Ā—č P –ł NP –Ĺ–Ķ —Ä–į–≤–Ĺ—č. –í –ļ–į—á–Ķ—Ā—ā–≤–Ķ –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–į —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł—Ź –ľ–ĺ–∂–Ĺ–ĺ –Ņ—Ä–ł–≤–Ķ—Ā—ā–ł –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ–ł–Ĺ–į–Ľ—Ć–Ĺ—É—é —Ä–Ķ–ī—É–ļ—Ü–ł—é –ļ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–Ķ Exact-3-SAT. . –Ě–Ķ—Ā–ľ–ĺ—ā—Ä—Ź –Ĺ–į –Ĺ–Ķ–∑–Ĺ–į—á–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ķ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ —É—Ā–Ľ–ĺ–≤–ł—Ź, –Ĺ–Ķ —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ–ł–Ĺ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –ī–į–Ĺ–Ĺ–ĺ–Ļ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ—č, –Ķ—Ā–Ľ–ł –ļ–Ľ–į—Ā—Ā—č P –ł NP –Ĺ–Ķ —Ä–į–≤–Ĺ—č. –í –ļ–į—á–Ķ—Ā—ā–≤–Ķ –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–į —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł—Ź –ľ–ĺ–∂–Ĺ–ĺ –Ņ—Ä–ł–≤–Ķ—Ā—ā–ł –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ–ł–Ĺ–į–Ľ—Ć–Ĺ—É—é —Ä–Ķ–ī—É–ļ—Ü–ł—é –ļ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–Ķ Exact-3-SAT.
–°–ľ. —ā–į–ļ–∂–Ķ
–ü—Ä–ł–ľ–Ķ—á–į–Ĺ–ł—Ź
- ‚ÜĎ –Ē–∂–ĺ–Ĺ –Ē–∂. –ě‚Äô–ö–ĺ–Ĺ–Ĺ–ĺ—Ä –ł –≠–ī–ľ—É–Ĺ–ī –§. –†–ĺ–Ī–Ķ—Ä—ā—Ā–ĺ–Ĺ. George Dantzig (–į–Ĺ–≥–Ľ.) ‚ÄĒ –Ī–ł–ĺ–≥—Ä–į—Ą–ł—Ź –≤ –į—Ä—Ö–ł–≤–Ķ MacTutor.
- ‚ÜĎ Cottle, Richard; Johnson, Ellis; Wets, Roger, ¬ęGeorge B. Dantzig (1914‚ÄĒ2005)¬Ľ –ź—Ä—Ö–ł–≤–Ĺ–į—Ź –ļ–ĺ–Ņ–ł—Ź –ĺ—ā 7 —Ā–Ķ–Ĺ—ā—Ź–Ī—Ä—Ź 2015 –Ĺ–į Wayback Machine, Notices of the American Mathematical Society, v.54, no.3, March 2007. Cf. p.348
- ‚ÜĎ 1 2 Hardesty, Larry, ¬ęFirst improvement of fundamental algorithm in 10 years¬Ľ –ź—Ä—Ö–ł–≤–Ĺ–į—Ź –ļ–ĺ–Ņ–ł—Ź –ĺ—ā 28 –ľ–į—Ä—ā–į 2014 –Ĺ–į Wayback Machine, MIT News Office, September 27, 2010
- ‚ÜĎ Bornd√∂rfer, Ralf; Gr√∂tschel, Martin; L√∂bel, Andreas, ¬ęAlcuin‚Äôs Transportation Problems and Integer Programing¬Ľ –ź—Ä—Ö–ł–≤–Ĺ–į—Ź –ļ–ĺ–Ņ–ł—Ź –ĺ—ā 7 –į–≤–≥—É—Ā—ā–į 2011 –Ĺ–į Wayback Machine, Konrad-Zuse-Zentrum f√ľr Informationstechnik, Berlin, Germany, November 1995. Cf. p.3
- ‚ÜĎ Powell, Stewart M., ¬ęThe Berlin Airlift¬Ľ, Air Force Magazine, June 1998.
- ‚ÜĎ Dantzig, G.B., ¬ęApplication of the Simplex Method to a Transportation Problem¬Ľ –ź—Ä—Ö–ł–≤–Ĺ–į—Ź –ļ–ĺ–Ņ–ł—Ź –ĺ—ā 19 –ł—é–Ľ—Ź 2010 –Ĺ–į Wayback Machine, in T.C. Koopman (ed.): Activity Analysis and Production and Allocation, New York, (1951) 359‚ÄĒ373.
- ‚ÜĎ Ford, L.R., Jr.; Fulkerson, D.R., ¬ęMaximal Flow through a Network¬Ľ, Canadian Journal of Mathematics (1956), pp.399-404.
- ‚ÜĎ Ford, L.R., Jr.; Fulkerson, D.R., Flows in Networks, Princeton University Press (1962).
- ‚ÜĎ Kelner, Jonathan, ¬ęElectrical Flows, Laplacian Systems and Faster Approximation of Maximum Flow in Undirected Graphs¬Ľ –ź—Ä—Ö–ł–≤–Ĺ–į—Ź –ļ–ĺ–Ņ–ł—Ź –ĺ—ā 24 –ł—é–Ĺ—Ź 2011 –Ĺ–į Wayback Machine, talk at CSAIL, MIT, Tuesday, September 28 2010
- ‚ÜĎ Electrical Flows, Laplacian Systems, and Faster Approximation of Maximum Flow in Undirected Graphs –ź—Ä—Ö–ł–≤–Ĺ–į—Ź –ļ–ĺ–Ņ–ł—Ź –ĺ—ā 29 –Ĺ–ĺ—Ź–Ī—Ä—Ź 2010 –Ĺ–į Wayback Machine, by Paul Cristiano et al., October 19, 2010.
- ‚ÜĎ –ź–Ľ–≥–ĺ—Ä–ł—ā–ľ –Ē–ł–Ĺ–ł—Ü–į (–Ĺ–Ķ–ĺ–Ņ—Ä.). –Ē–į—ā–į –ĺ–Ī—Ä–į—Č–Ķ–Ĺ–ł—Ź: 28 –ĺ–ļ—ā—Ź–Ī—Ä—Ź 2010. –ź—Ä—Ö–ł–≤–ł—Ä–ĺ–≤–į–Ĺ–ĺ 7 –ľ–į—Ź 2015 –≥–ĺ–ī–į.
–õ–ł—ā–Ķ—Ä–į—ā—É—Ä–į
- Schrijver, Alexander, ¬ęOn the history of the transportation and maximum flow problems¬Ľ, Mathematical Programming 91 (2002) 437‚ÄĒ445
- –ö–ĺ—Ä–ľ–Ķ–Ĺ, –Ę., –õ–Ķ–Ļ–∑–Ķ—Ä—Ā–ĺ–Ĺ, –ß., –†–ł–≤–Ķ—Ā—ā, –†., –®—ā–į–Ļ–Ĺ, –ö. –ź–Ľ–≥–ĺ—Ä–ł—ā–ľ—č: –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ –ł –į–Ĺ–į–Ľ–ł–∑ = Introduction to Algorithms / –ü–ĺ–ī —Ä–Ķ–ī. –ė. –í. –ö—Ä–į—Ā–ł–ļ–ĺ–≤–į. ‚ÄĒ 2-–Ķ –ł–∑–ī. ‚ÄĒ –ú.: –í–ł–Ľ—Ć—Ź–ľ—Ā, 2005. ‚ÄĒ 1296 —Ā. ‚ÄĒ ISBN 5-8459-0857-4.. –ď–Ľ–į–≤–į 26. –ú–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ—č–Ļ –Ņ–ĺ—ā–ĺ–ļ.
- ‚ÜĎ Andrew V. Goldberg and S. Rao. Beyond the flow decomposition barrier (–Ĺ–Ķ–ĺ–Ņ—Ä.) // J. Assoc. Comput. Mach.. ‚ÄĒ 1998. ‚ÄĒ –Ę. 45. ‚ÄĒ –°. 753‚ÄĒ782. ‚ÄĒ doi:10.1145/290179.290181.
- ‚ÜĎ Andrew V. Goldberg and Robert E. Tarjan. A new approach to the maximum-flow problem (–į–Ĺ–≥–Ľ.) // Journal of the ACM : journal. ‚ÄĒ ACM Press, 1988. ‚ÄĒ Vol. 35, no. 4. ‚ÄĒ P. 921‚ÄĒ940. ‚ÄĒ ISSN 0004-5411. ‚ÄĒ doi:10.1145/48014.61051.
- ‚ÜĎ Joseph Cheriyan and Kurt Mehlhorn. An analysis of the highest-level selection rule in the preflow-push max-flow algorithm (–į–Ĺ–≥–Ľ.) // Information Processing Letters[–į–Ĺ–≥–Ľ.] : journal. ‚ÄĒ 1999. ‚ÄĒ Vol. 69, no. 5. ‚ÄĒ P. 239‚ÄĒ242. ‚ÄĒ doi:10.1016/S0020-0190(99)00019-8.
- ‚ÜĎ Daniel D. Sleator and Robert E. Tarjan. A data structure for dynamic trees (–į–Ĺ–≥–Ľ.) // Journal of Computer and System Sciences[–į–Ĺ–≥–Ľ.] : journal. ‚ÄĒ 1983. ‚ÄĒ Vol. 26, no. 3. ‚ÄĒ P. 362‚ÄĒ391. ‚ÄĒ ISSN 0022-0000. ‚ÄĒ doi:10.1016/0022-0000(83)90006-5.
- ‚ÜĎ Daniel D. Sleator and Robert E. Tarjan. Self-adjusting binary search trees (–į–Ĺ–≥–Ľ.) // Journal of the ACM : journal. ‚ÄĒ ACM Press, 1985. ‚ÄĒ Vol. 32, no. 3. ‚ÄĒ P. 652‚ÄĒ686. ‚ÄĒ ISSN 0004-5411. ‚ÄĒ doi:10.1145/3828.3835.
- Eugene Lawler[–į–Ĺ–≥–Ľ.]. 4. Network Flows // Combinatorial Optimization: Networks and Matroids (–į–Ĺ–≥–Ľ.). ‚ÄĒ Dover, 2001. ‚ÄĒ P. 109‚ÄĒ177. ‚ÄĒ ISBN 0486414531.
|























































