Комплексная амплитуда

Компле́ксная амплитуда (англ. phasor) — комплексная величина, модуль и аргумент которой равны соответственно амплитуде и начальной фазе гармонического сигнала.

Пусть имеется гармонический сигнал:

${\displaystyle a(t)=A\cos \left(\omega t+\phi \right),}$

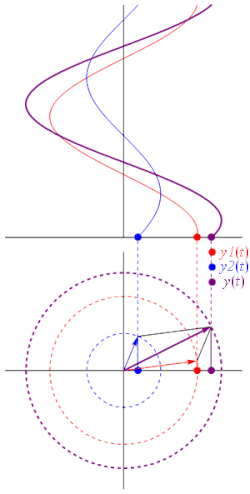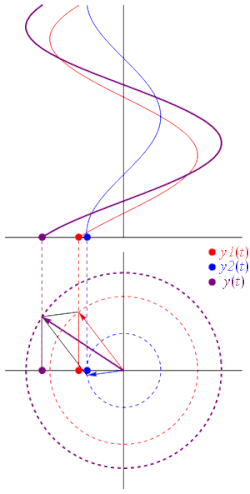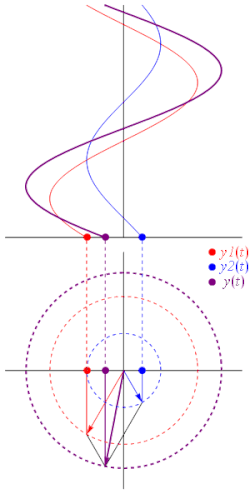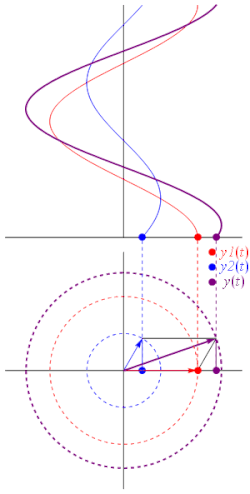где A — амплитуда сигнала, ω — циклическая частота, ϕ — начальная фаза.

Над сигналами, записанными в подобной форме, алгебраически неудобно производить такие арифметические операции, как сложение двух сигналов, вычитание из одного сигнала другого сигнала. С целью облегчения этих операций гармонические сигналы представляют в виде комплексного числа, модуль которого равен амплитуде сигнала, а аргумент — фазе сигнала. Воспользовавшись формулой Эйлера:

${\displaystyle Ae^{i(\omega t+\phi )}=A\ cos(\omega t+\phi )+iAsin(\omega t+\phi )}$.

Оригинальный сигнал a(t) равен действительной части данного комплексного числа:

${\displaystyle a(t)=\Re (Ae^{i(\omega t+\phi )})}$

При этом ${\displaystyle Ae^{i(\omega t+\phi )}=Ae^{i\phi }e^{i\omega t}={\dot {A}}e^{i\omega t}}$,

тогда комплексная амплитуда гармонического сигнала определяется следующим выражением:

${\displaystyle {\dot {A}}=Ae^{i\phi }}$.

Если рассматривать комплексную амплитуду как комплексное число в алгебраической форме, то действительная часть соответствует амплитуде косинусной (синфазной) компоненты, а мнимая — амплитуде синусной (квадратурной) компоненты исходного сигнала. Так, для сигнала (1) имеем: ${\displaystyle a(t)=\Re ({\dot {A}})\cos(\omega t)-\Im ({\dot {A}})\sin(\omega t)}$

где ${\displaystyle \Re ({\dot {A}})=A\cos(\phi ),\quad \Im ({\dot {A}})=A\sin(\phi )}$

Если рассматривать комплексную амплитуду как комплексное число в тригонометрической форме, то модуль соответствует амплитуде исходного гармонического сигнала, а аргумент — сдвигу фазы исходного гармонического сигнала относительно сигнала ${\displaystyle \cos {(\omega t)}}$.

К сигналам в пространстве комплексных амплитуд могут быть применены линейные операции. Другими словами, перечисленные ниже операции над комплексными амплитудами:

• умножение комплексной амплитуды на константу
• сложение комплексных амплитуд (соответствующих одной и той же частоте)
• вычитание комплексных амплитуд (соответствующих одной и той же частоте)
• интегрирование комплексной амплитуды по времени
• дифференцирование комплексной амплитуды по времени

приводят к такому же результату, как если бы они были проделаны над соответствующими гармоническими сигналами, а затем от них взята комплексная амплитуда.

Несмотря на то, что в выражение для комплексной амплитуды не входит частота ω гармонического сигнала, следует помнить, что комплексная амплитуда описывает гармонический сигнал конкретной частоты. Поэтому в пространстве комплексных амплитуд недопустимы операции, которые:

• принимают в качестве операндов комплексные амплитуды, описывающие гармонические сигналы разных частот.
• меняют частоту гармонического сигнала или порождают новые частоты (все нелинейные операции, например, перемножение двух сигналов).

Комплексная амплитуда является полным и очень удобным способом описания гармонических сигналов, поскольку:

• Характеризует и амплитуду, и фазу
• Не содержит зависимости от времени
• Позволяет использовать векторные диаграммы для анализа цепей на переменном токе

Использование комплексных амплитуд и импедансов позволяет свести задачу прохождения гармонического сигнала через линейную цепь (описывается системой дифференциальных уравнений) к более простой задаче, эквивалентной анализу цепи из резисторов на постоянном токе (описывается системой алгебраических уравнений).

• Метод комплексных амплитуд
• Формула Эйлера

В статье не хватает ссылок на источники (см. рекомендации по поиску). Информация должна быть проверяема, иначе она может быть удалена. Вы можете отредактировать статью, добавив ссылки на авторитетные источники в виде сносок. (20 октября 2024)