–õ–ĺ–≥–į—Ä–ł—Ą–ľ–ł—á–Ķ—Ā–ļ–į—Ź —Ā–ł—Ā—ā–Ķ–ľ–į —Ā—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź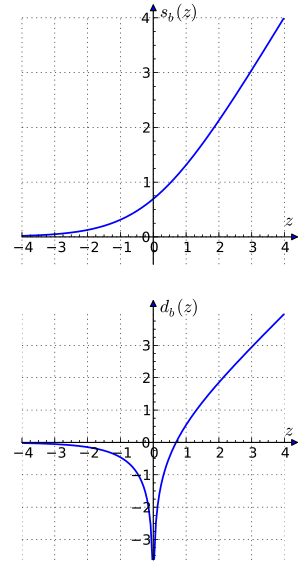 –õ–ĺ–≥–į—Ä–ł—Ą–ľ–ł—á–Ķ—Ā–ļ–į—Ź —Ā–ł—Ā—ā–Ķ–ľ–į —Ā—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź (LNS) ‚ÄĒ —ć—ā–ĺ –į—Ä–ł—Ą–ľ–Ķ—ā–ł—á–Ķ—Ā–ļ–į—Ź —Ā–ł—Ā—ā–Ķ–ľ–į, –ł–Ĺ–ĺ–≥–ī–į –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ–ľ–į—Ź –ī–Ľ—Ź –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł—Ź –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č—Ö —á–ł—Ā–Ķ–Ľ –≤ –ļ–ĺ–ľ–Ņ—Ć—é—ā–Ķ—Ä–Ķ –ł –≤ —Ü–ł—Ą—Ä–ĺ–≤—č—Ö –į–Ņ–Ņ–į—Ä–į—ā–Ĺ—č—Ö —Ā—Ä–Ķ–ī—Ā—ā–≤–į—Ö, –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–Ĺ–ĺ –≤ —Ü–ł—Ą—Ä–ĺ–≤–ĺ–Ļ –ĺ–Ī—Ä–į–Ī–ĺ—ā–ļ–Ķ —Ā–ł–≥–Ĺ–į–Ľ–ĺ–≤. –Ę–Ķ–ĺ—Ä–ł—Ź–í LNS —á–ł—Ā–Ľ–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ĺ –Ľ–ĺ–≥–į—Ä–ł—Ą–ľ–ĺ–ľ —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ: –≥–ī–Ķ - –Ķ–≥–ĺ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ; –ĺ–Ī–ĺ–∑–Ĺ–į—á–į—é—Č–ł–Ļ –∑–Ĺ–į–ļ ( –Ķ—Ā–Ľ–ł –ł –Ķ—Ā–Ľ–ł ). –≠—ā–į —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–į —É–Ņ—Ä–ĺ—Č–į–Ķ—ā –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł—Ź, –ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź, –≤–ĺ–∑–≤–Ķ–ī–Ķ–Ĺ–ł—Ź –≤ —Ā—ā–Ķ–Ņ–Ķ–Ĺ—Ć, —ā–į–ļ –ļ–į–ļ –ĺ–Ĺ–ł —Ā–≤–ĺ–ī—Ź—ā—Ā—Ź –ļ —Ā–Ľ–ĺ–∂–Ķ–Ĺ–ł—é, –≤—č—á–ł—ā–į–Ĺ–ł—é, —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł—é –ł –ī–Ķ–Ľ–Ķ–Ĺ–ł—é, —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –° –ī—Ä—É–≥–ĺ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č, –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł —Ā–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –ł –≤—č—á–ł—ā–į–Ĺ–ł—Ź –≤ —ā–į–ļ–ĺ–Ļ —Ą–ĺ—Ä–ľ–Ķ –∑–į–Ņ–ł—Ā–ł –ĺ–ļ–į–∑—č–≤–į—é—ā—Ā—Ź –Ī–ĺ–Ľ–Ķ–Ķ —Ā–Ľ–ĺ–∂–Ĺ—č–ľ–ł, –ł –ĺ–Ĺ–ł —Ä–į—Ā—Ā—á–ł—ā—č–≤–į—é—ā—Ā—Ź –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–į–ľ: –≥–ī–Ķ —Ä–į–∑–Ĺ–ł—Ü–į –ľ–Ķ–∂–ī—É –Ľ–ĺ–≥–į—Ä–ł—Ą–ľ–į–ľ–ł –ĺ–Ņ–Ķ—Ä–į–Ĺ–ī–ĺ–≤, —Ą—É–Ĺ–ļ—Ü–ł—Ź ¬ę—Ā—É–ľ–ľ—謼 , –į —Ą—É–Ĺ–ļ—Ü–ł—Ź ¬ę—Ä–į–∑–Ĺ–ł—ܗ謼 . –≠—ā–ł —Ą—É–Ĺ–ļ—Ü–ł–ł –ł , –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–Ĺ—č–Ķ –Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ —Ā–Ņ—Ä–į–≤–į, —ā–į–ļ–∂–Ķ –ł–∑–≤–Ķ—Ā—ā–Ĺ—č –ļ–į–ļ –Ľ–ĺ–≥–į—Ä–ł—Ą–ľ—č –ď–į—É—Ā—Ā–į. –£–Ņ—Ä–ĺ—Č–Ķ–Ĺ–ł–Ķ —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł—Ź, –ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź, –≤–∑—Ź—ā–ł—Ź –ļ–ĺ—Ä–Ĺ—Ź –ł –≤–ĺ–∑–≤–Ķ–ī–Ķ–Ĺ–ł—Ź –≤ —Ā—ā–Ķ–Ņ–Ķ–Ĺ—Ć –ļ–ĺ–ľ–Ņ–Ķ–Ĺ—Ā–ł—Ä—É–Ķ—ā—Ā—Ź —Ā–Ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć—é –ĺ—Ü–Ķ–Ĺ–ļ–ł —ć—ā–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ –ī–Ľ—Ź —Ā–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –ł –≤—č—á–ł—ā–į–Ĺ–ł—Ź. –≠—ā–į –ī–ĺ–Ī–į–≤–Ľ–Ķ–Ĺ–Ĺ–į—Ź —Ā—ā–ĺ–ł–ľ–ĺ—Ā—ā—Ć –ĺ—Ü–Ķ–Ĺ–ļ–ł –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ĺ–Ķ–∑–Ĺ–į—á–ł—ā–Ķ–Ľ—Ć–Ĺ–į –Ņ—Ä–ł –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–ł LNS –≤ –Ņ–Ķ—Ä–≤—É—é –ĺ—á–Ķ—Ä–Ķ–ī—Ć –ī–Ľ—Ź –Ņ–ĺ–≤—č—ą–Ķ–Ĺ–ł—Ź —ā–ĺ—á–Ĺ–ĺ—Ā—ā–ł –ĺ–Ņ–Ķ—Ä–į—Ü–ł–Ļ —Ā –Ņ–Ľ–į–≤–į—é—Č–Ķ–Ļ –∑–į–Ņ—Ź—ā–ĺ–Ļ. –ė—Ā—ā–ĺ—Ä–ł—Ź–õ–ĺ–≥–į—Ä–ł—Ą–ľ–ł—á–Ķ—Ā–ļ–į—Ź —Ā–ł—Ā—ā–Ķ–ľ–į —Ā—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź –Ī—č–Ľ–į –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ–ĺ –ł–∑–ĺ–Ī—Ä–Ķ—ā–Ķ–Ĺ–į –ł –ĺ–Ņ—É–Ī–Ľ–ł–ļ–ĺ–≤–į–Ĺ–į –Ņ–ĺ –ļ—Ä–į–Ļ–Ĺ–Ķ–Ļ –ľ–Ķ—Ä–Ķ —ā—Ä–ł —Ä–į–∑–į, –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –į–Ľ—Ć—ā–Ķ—Ä–Ĺ–į—ā–ł–≤—č —Ā–ł—Ā—ā–Ķ–ľ–į–ľ —Ā—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź —Ā —Ą–ł–ļ—Ā–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ļ –ł —Ā –Ņ–Ľ–į–≤–į—é—Č–Ķ–Ļ –∑–į–Ņ—Ź—ā–ĺ–Ļ[1]. –ö–ł–Ĺ–≥—Ā–Ī–Ķ—Ä–ł –ł –†–Ķ–Ļ–Ĺ–Ķ—Ä –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł–Ľ–ł ¬ę–Ľ–ĺ–≥–į—Ä–ł—Ą–ľ–ł—á–Ķ—Ā–ļ—É—é –į—Ä–ł—Ą–ľ–Ķ—ā–ł–ļ—ɬĽ –ī–Ľ—Ź —Ü–ł—Ą—Ä–ĺ–≤–ĺ–Ļ –ĺ–Ī—Ä–į–Ī–ĺ—ā–ļ–ł —Ā–ł–≥–Ĺ–į–Ľ–ĺ–≤ –≤ 1971 –≥–ĺ–ī—É.[2] –ź–Ĺ–į–Ľ–ĺ–≥–ł—á–Ĺ–į—Ź LNS –Ī—č–Ľ–į –ĺ–Ņ–ł—Ā–į–Ĺ–į –≤ 1975 –≥–ĺ–ī—É –®–≤–į—Ä—Ü–Ľ–Ķ–Ĺ–ī–Ķ—Ä–ĺ–ľ –ł –ź–Ľ–Ķ—Ö–ĺ–Ņ–ĺ—É–Ľ–ĺ—Ā–ĺ–ľ.[3] –õ–ł –ł –≠–ī–≥–į—Ä –ĺ–Ņ–ł—Ā–į–Ľ –Ņ–ĺ–ī–ĺ–Ī–Ĺ—É—é —Ā–ł—Ā—ā–Ķ–ľ—É —Ā—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź, –ļ–ĺ—ā–ĺ—Ä—É—é –ĺ–Ĺ–ł –Ĺ–į–∑–≤–į–Ľ–ł ¬ę–§–ĺ–ļ—É—Ā¬Ľ, –≤ 1977 –≥–ĺ–ī—É[4] –ú–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł–Ķ –ĺ—Ā–Ĺ–ĺ–≤—č –ī–Ľ—Ź —Ā–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –ł –≤—č—á–ł—ā–į–Ĺ–ł—Ź –≤ LNS –≤–ĺ—Ā—Ö–ĺ–ī—Ź—ā –ļ –ö–į—Ä–Ľ—É –§—Ä–ł–ī—Ä–ł—Ö—É –ď–į—É—Ā—Ā—É –ł Z. Leonelli[5][6]. –ü—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–ĶLNS –Ī—č–Ľ–į –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–į –≤ Gravity Pipe[–į–Ĺ–≥–Ľ.] (GRAPE) ‚ÄĒ —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ–ĺ–ľ —Ā—É–Ņ–Ķ—Ä–ļ–ĺ–ľ–Ņ—Ć—é—ā–Ķ—Ä–Ķ[7], –ļ–ĺ—ā–ĺ—Ä—č–Ļ –≤—č–ł–≥—Ä–į–Ľ –ü—Ä–Ķ–ľ–ł—é –ď–ĺ—Ä–ī–ĺ–Ĺ–į –Ď–Ķ–Ľ–Ľ–į –≤ 1999 –≥–ĺ–ī—É. LNS –ĺ–Ī—č—á–Ĺ–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź –ļ–į–ļ —á–į—Ā—ā—Ć —Ā–ļ—Ä—č—ā—č—Ö –ľ–į—Ä–ļ–ĺ–≤—Ā–ļ–ł—Ö –ľ–ĺ–ī–Ķ–Ľ–Ķ–Ļ, —ā–į–ļ–ł—Ö –ļ–į–ļ –ź–Ľ–≥–ĺ—Ä–ł—ā–ľ –í–ł—ā–Ķ—Ä–Ī–ł, –ī–Ľ—Ź —Ä–į—Ā–Ņ–ĺ–∑–Ĺ–į–≤–į–Ĺ–ł—Ź —Ä–Ķ—á–ł –ł —Ā–Ķ–ļ–≤–Ķ–Ĺ–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź –Ē–Ě–ö. –ó–Ĺ–į—á–ł—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ —É—Ā–ł–Ľ–ł—Ź –≤ –ł—Ā—Ā–Ľ–Ķ–ī–ĺ–≤–į–Ĺ–ł–ł –Ņ—Ä–ł–ľ–Ķ–Ĺ–ł–ľ–ĺ—Ā—ā–ł LNS –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –∂–ł–∑–Ĺ–Ķ—Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ–Ļ –į–Ľ—Ć—ā–Ķ—Ä–Ĺ–į—ā–ł–≤—č —Ā–ł—Ā—ā–Ķ–ľ–į–ľ —Ā –Ņ–Ľ–į–≤–į—é—Č–Ķ–Ļ –∑–į–Ņ—Ź—ā–ĺ–Ļ –ĺ–Ī—Č–Ķ–≥–ĺ –Ĺ–į–∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –ī–Ľ—Ź –ĺ–Ī—Ä–į–Ī–ĺ—ā–ļ–ł –ĺ–ī–ł–Ĺ–į—Ä–Ĺ–ĺ–Ļ —ā–ĺ—á–Ĺ–ĺ—Ā—ā–ł –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č—Ö —á–ł—Ā–Ķ–Ľ –ĺ–Ņ–ł—Ā–į–Ĺ—č –≤ –ļ–ĺ–Ĺ—ā–Ķ–ļ—Ā—ā–Ķ ¬ę–ē–≤—Ä–ĺ–Ņ–Ķ–Ļ—Ā–ļ–ĺ–≥–ĺ –Ľ–ĺ–≥–į—Ä–ł—Ą–ľ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ľ–ł–ļ—Ä–ĺ–Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ—Ä–į¬Ľ (ELM).[8] –ü—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ –Ņ—Ä–ĺ—ā–ĺ—ā–ł–Ņ 32-—Ä–į–∑—Ä—Ź–ī–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ—Ä–į, —Ą—É–Ĺ–ļ—Ü–ł–ĺ–Ĺ–ł—Ä—É—é—Č–Ķ–≥–ĺ –≤ LNS. –Ē–į–Ľ—Ć–Ĺ–Ķ–Ļ—ą–Ķ–Ķ —Ā–ĺ–≤–Ķ—Ä—ą–Ķ–Ĺ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł–Ķ LNS, –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ļ –Ĺ–į –į—Ä—Ö–ł—ā–Ķ–ļ—ā—É—Ä–Ķ ELM –≤–Ĺ–ĺ–≤—Ć –Ņ–ĺ–ļ–į–∑–į–Ľ–ĺ –∑–Ĺ–į—á–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ľ—É—á—ą—É—é —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—Ć –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł–Ļ –ł –Ī–ĺ–Ľ—Ć—ą—É—é —ā–ĺ—á–Ĺ–ĺ—Ā—ā—Ć, –Ĺ–Ķ–∂–Ķ–Ľ–ł –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź —Ā –Ņ–Ľ–į–≤–į—é—Č–Ķ–Ļ –∑–į–Ņ—Ź—ā–ĺ–Ļ.[9] LNS –ł–Ĺ–ĺ–≥–ī–į –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź –≤ FPGA ‚ÄĒ –Ņ—Ä–ł–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź—Ö, –≥–ī–Ķ –Ī–ĺ–Ľ—Ć—ą–ł–Ĺ—Ā—ā–≤–ĺ –į—Ä–ł—Ą–ľ–Ķ—ā–ł—á–Ķ—Ā–ļ–ł—Ö –ĺ–Ņ–Ķ—Ä–į—Ü–ł–Ļ —ć—ā–ĺ —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ –ł –ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ.[10] –ü—Ä–ł–ľ–Ķ—á–į–Ĺ–ł—Ź
–°—Ā—č–Ľ–ļ–ł |
Portal di Ensiklopedia Dunia




























