Пространственный многоугольник

Пространственный многоугольник^[1] — многоугольник, вершины которого не компланарны. Пространственные многоугольники должны иметь по меньшей мере 4 вершины. Внутренняя поверхность таких многоугольников однозначно не определяется.

Пространственные бесконечноугольники^[англ.] (апейрогоны) имеют вершины, не все из которых коллинеарны.

Зигзаг-многоугольник, или антипризматический многоугольник^[2], имеет вершины, которые попеременно находятся на двух параллельных плоскостях, а потому, должны иметь чётное число сторон.

Правильный пространственный многоугольник в 3-мерном пространстве (и правильные пространственные бесконечноугольники^[англ.] в 2-двумерном) всегда являются зигзаг-многоугольниками.

Правильный пространственный многоугольник является изогональной фигурой с одинаковыми длинами сторон. В 3-мерном пространстве правильные пространственные многоугольники являются зигзаг-многоугольниками (антирпизматическими многоугольниками), вершины которых поочерёдно принадлежат двум параллельным плоскостям. Стороны n-антипризмы могут определять правильный пространственный 2n-угольник.

Правильному пространственному n-угольнику можно дать обозначение {p}#{ } как смесь обозначений правильного многоугольника {p} и ортогонального отрезка { }^[3]. Симметрия между последовательными вершинами является скользящей.

Ниже в примерах показаны однородные квадратные и пятиугольные антипризмы. Звёздные антипризмы^[англ.] также образуют правильные пространственные многоугольники с различным способом соединения вершин верхней и нижней звёзд.

Правильные зигзаг-многоугольники

Пространственный квадрат	Пространственный шестиугольник	Пространственный восьмиугольник
{2}#{ }	{3}#{ }	{4}#{ }
sr{2,2}	sr{2,3}	sr{2,4}

Пространственный десятиугольник
{5}#{ }	{5/2}#{ }	{5/3}#{ }
sr{2,5}	sr{2,5/2}[англ.]	sr{2,5/3}[англ.]

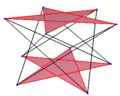
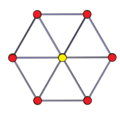
Правильный сложный пространственный 2n-угольник можно построить путём добавления второго пространственного 2n-угольника, полученного вращением первого. В этом случае вершины каждого из составляющих 2n-угольников лежат в вершинах призматической комбинации антипризм^[англ.].

Правильная комбинация пространственных зигзаг-многоугольников

Пространственные квадраты		Пространственные шестиугольники	Пространственные десятиугольники
Два {2}#{ }	Три {3}#{ }	Два {3}#{ }	Два {5/3}#{ }

Многоугольники Петри — это правильные пространственные многоугольники, задаваемые внутри правильных многогранников и политопов. Например, 5 платоновых тел содержат 4, 6 и 10-сторонние правильные пространственные многоугольники, как видно из этих ортогональных проекций (красными отрезками показана проективная оболочка^[англ.]). Тетраэдр и октаэдр включают все вершины в зигзаг-многоугольника и могут рассматриваться как антпризмы отрезков и треугольников соответственно.

Косой многоугольник^[англ.] имеет правильные грани или вершинные фигуры в виде правильных пространственных многоугольников. Имеется бесконечно много заполняющих всё пространство правильных косых многоугольников^[англ.] в 3-мерном пространстве и существуют косые многоугольники в 4-мерном пространстве, некоторые в виде однородного 4-мерного многогранника^[англ.].

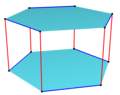
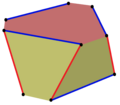
вершинные фигуры трёх бесконечных правильных косых многоугольников

{4,6|4}	{6,4|4}	{6,6|3}
Правильный косой шестиугольник {3}#{ }	Правильный косой квадрат {2}#{ }	Правильный косой шестиугольник {3}#{ }

Изогональный пространственный многоугольник — это пространственный многоугольник с вершинами одного типа, соединёнными двумя типами сторон. Изогональные пространственные многоугольники с равными длинами сторон можно считать полуправильными. Они подобны зигзаг-многоугольникам на двух плоскостях, за исключением того, что сторонам позволяется как переходить на другую плоскость, так и оставаться на той же плоскости.

Изогональные пространственные многоугольники можно получить на n-угольных призмах с чётным числом сторон, попеременно двигаясь по сторонам многоугольника и между многоугольниками. Например, по вершинам куба — проходим вершины вертикально по красным рёбрам и по синим рёбрам вдоль сторон квадратов оснований.

Куб, квадрат-диагональ	Витая призма[англ.]	Куб	Пересечённый куб
Шестигранная призма[англ.]	Шестигранная призма	Шестигранная призма

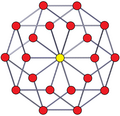
В 4-мерном пространстве правильные пространственные многоугольники могут иметь вершины на торе Клиффорда и связаны смещением Клиффорда^[англ.]. В отличие от зигзаг-многоугольников, пространственные многоугольники двойного вращения могут иметь нечётное число сторон.

Многоугольники Петри правильного 4-мерного многогранника определяют правильные пространственные многоугольники. Число Кокстера для каждой группы симметрий Коксетера выражает, сколько сторон имеет многоугольник Петри. Так, это будет 5-сторонний многоугольник для пятиячейника, 8-сторонний для тессеракта и шестнадцатиячейника, 12 сторон для двадцатичетырёхячейника и 30 сторон для стодвадцатиячейника и шестисотячейника.

Если ортогонально спроектировать эти правильные пространственные многоугольники на плоскость Коксетера^[англ.], они превращаются в правильные огибающие многоугольники на плоскости.

A4, [3,3,3]	B4, [4,3,3]		F4, [3,4,3]	H4, [5,3,3]
Пятиугольник, Пентаграмма	Восьмиугольник		Двенадцатиугольник	Тридцатиугольник
пятиячейник {3,3,3}	тессеракт {4,3,3}	шестнадцатиячейник {3,3,4}	двадцатичетырёхячейник {3,4,3}	стодвадцатиячейник {5,3,3}	шестисотячейник {3,3,5}

n-n дуопризма и двойственная дуопирамида^[англ.] также имеют 2n-сторонние полигоны Петри. (тессеракт является 4-4 дуопризмой, а шестнадцатиячейник — 4-4 дуопирамидой.)

Шестиугольник		Десятиугольник		Двенадцатиугольник
3-3 дуопризма	3-3 дуопирамида	5,5-дуопризма	5-5 дуопирамида[англ.]	6-6 дуопризма[англ.]	6-6 дуопирамида[англ.]

• Косой многоугольник^[англ.]
• Косой бесконечноугольник^[англ.]
• Многоугольник Петри
• Скрещивающиеся прямые

• Peter McMullen, Egon Schulte. Abstract Regular Polytopes // 1st. — Cambridge University Press, December 2002. — ISBN 0-521-81496-0.
• Robert Williams. Skew Polygons (Saddle Polygons). §2.2 // The Geometrical Foundation of Natural Structure: A Source Book of Design. — Dover Publications, Inc., 1979. — ISBN 0-486-23729-X.
• H. S. M.Coxeter. Chapter 1. Regular polygons, 1.5. Regular polygons in n dimensions, 1.7. Zigzag and antiprismatic polygons, 1.8. Helical polygons. 4.3. Flags and Orthoschemes, 11.3. Petrie polygons // Regular complex polytopes. — 1974.
• H. S. M.Coxeter. Разделы 2.6 Petrie Polygons с.24—25, Chapter 12, с.213—235, The generalized Petrie polygon // Regular Polytopes^[англ.]. — 3rd ed. — New York: Dover, 1973.
• H. S. M. Coxeter, W. O. J. Moser. 5.2 The Petrie polygon {p,q}. // Generators and Relations for Discrete Groups. — New York: Springer-Verlag, 1980 (1st ed, 1957). — ISBN 0-387-09212-9.
• John Milnor. On the total curvature of knots // Ann. Math. — 1950. — Т. 52. — С. 248—257.
• J.M. Sullivan^[англ.]. Curves of finite total curvature. — Technische Universität Berlin, 2006. — Июль. — arXiv:math.0606007v2.

• Weisstein, Eric W. Skew polygon (англ.) на сайте Wolfram MathWorld.
• Weisstein, Eric W. Petrie polygon (англ.) на сайте Wolfram MathWorld.

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Пожалуйста, после исправления проблемы исключите её из списка параметров. После устранения всех недостатков этот шаблон может быть удалён любым участником.