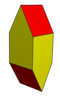
Стереоэдр

Стереоэдр — это выпуклый многогранник, который заполняет пространство гранетранзитивно, что означает, что симметрии мозаики переносят одну копию стереоэдра в любую другую.

Двумерные аналоги стереоэдров называются планигонами. Многогранники более высоких размерностей таже могут быть стереоэдрами.

Подмножество стереоэдров назывется плезиоэдр^?!ами, они определяются как ячейки Вороного симметричного множества Делоне.

Параллелоэдры — это заполняющие пространство плезиоэдры с использованием только параллельного переноса. Ниже на рисунках параллельные рёбра выделены разным цветом.

Параллелоэдры

куб	шестиугольная призма	ромбододекаэдр	удлиннённый двенадцатигранник[англ.]	усечённый октаэдр

Катоптрическое замощение^[англ.] содержит стереоэдральные ячейки. Двугранные углы делят 180° нацело и выкрашены согласно их порядку. Первые три области являются фундаментальными областями симметрий ${\displaystyle {\tilde {C}}_{3}}$, ${\displaystyle {\tilde {B}}_{3}}$ и ${\displaystyle {\tilde {A}}_{3}}$, которые представляют диаграммы Коксетера — Дынкин , и . ${\displaystyle {\tilde {B}}_{3}}$ является половиной симметрии ${\displaystyle {\tilde {C}}_{3}}$, а ${\displaystyle {\tilde {A}}_{3}}$ является четвертью симметрии.

Любой заполняющий пространство стереоэдр с симметрией может быть разрезан на более мелкие равные ячейки, которые также являются стереоэдрами. Ниже в названиях отражено такое разрезание.

Катоптрические ячейки

Faces	4				5			6				8	12
Type	Тетраэдр				Квадратная пирамида			Треугольная бипирамида		Куб		Октаэдр	Ромбододекаэдр
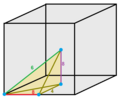
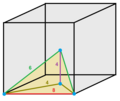
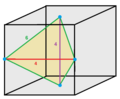
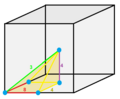
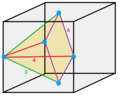
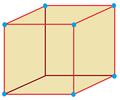
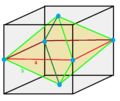
Изображения	1/48 (1)	1/24 (2)	1/12 (4)	1/12 (4)	1/24 (2)	1/6 (8)	1/6 (8)	1/12 (4)	1/4 (12)	1 (48)	1/2 (24)	1/3 (16)	2 (96)
Симметрия (порядок)	C1 1	C1v 2	D2d 4	C1v 2	C1v 2	C4v 8	C2v 4	C2v 4	C3v 6	Oh 48	D3d 12	D4h 16	Oh 48
Соты	Одна восьмая пирамиды	Треугольная пирамида	Сплюснуто тетраэдральные	Половина пирамиды	Четверть квадратной пирамиды	Пирамида	Половина сплюснутого восьмигранник	Четверть сплюснутого восьмигранника	Четверть куба	Куб	Сплюснутый куб	Сплюснутый октаэдр	Додекаэдр

Другие выпуклые многогранники, являющиеся стереоэдрами, но ни параллелоэдрами, ни плезиоэдрами.

Другие

Грани	8		10	12
Симметрия (порядок)	D2d (8)			D4h (16)
Изображения
Ячейка	Двускатный повернутый бикупол	Удлиннённый двускатный повернутый бикупол[англ.]	Десятигранник из десяти алмазов[англ.]	Удлинённая четырёхугольная бипирамида

• А. Б. Иванов. Стереоэдр.
• Математическая энциклопедия / под редакцией И. М. Виноградова. — Советская энциклопедия, 1985. — Т. 5. — С. 228-229.
• Б. Н. Делоне, Н. Н. Сандакова. Теория стереоэдров // Тр. МИАН СССР. — АН СССР, 1961. — Т. 64. — С. 28–51.
• Goldberg, Michael Three Infinite Families of Tetrahedral Space-Fillers Journal of Combinatorial Theory A, 16, pp. 348–354, 1974.
• Goldberg, Michael The space-filling pentahedra, Journal of Combinatorial Theory, Series A Volume 13, Issue 3, November 1972, Pages 437-443 [1] PDF
• Goldberg, Michael The Space-filling Pentahedra II, Journal of Combinatorial Theory 17 (1974), 375–378. PDF
• Goldberg, Michael On the space-filling hexahedra Geom. Dedicata, June 1977, Volume 6, Issue 1, pp 99–108 [2] PDF
• Goldberg, Michael On the space-filling heptahedra Geometriae Dedicata, June 1978, Volume 7, Issue 2, pp 175–184 [3] PDF
• Goldberg, Michael Convex Polyhedral Space-Fillers of More than Twelve Faces. Geom. Dedicata 8, 491-500, 1979.
• Goldberg, Michael On the space-filling octahedra, Geometriae Dedicata, January 1981, Volume 10, Issue 1, pp 323–335 [4] PDF
• Goldberg, Michael On the Space-filling Decahedra. Structural Topology, 1982, num. Type 10-II PDF
• Goldberg, Michael On the space-filling enneahedra Geometriae Dedicata, June 1982, Volume 12, Issue 3, pp 297–306 [5] PDF