Точка сочленения

Точкой сочленения (англ. articulation point) в теории графов называется вершина графа, при удалении которой количество компонент связности возрастает. Для обозначения этого понятия также используются термины «разделяющая вершина» и «шарнир».

Вершина ${\displaystyle v}$ графа ${\displaystyle G}$ называется шарниром, если подграф ${\displaystyle G_{1}}$, полученный из графа ${\displaystyle G}$ удалением вершины ${\displaystyle v}$ и всех инцидентных ей рёбер, состоит из большего количества компонент связности, чем исходный граф 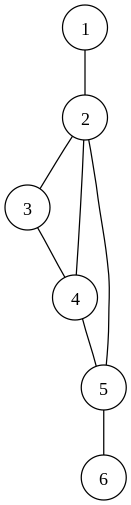${\displaystyle G}$.

С понятием шарнира также связано понятие двусвязности. Двусвязный граф - связный граф, не содержащий шарниров. Компонента двусвязности - максимальный (по включению) двусвязный подграф исходного графа. Компоненты двусвязности иногда называют блоками.

Рёберным аналогом шарнира является мост. Мостом называется такое ребро графа, в результате удаления которого количество компонент связности в графе возрастает.

Эффективное решение задачи поиска всех шарниров графа основано на алгоритме поиска в глубину.

Пусть дан граф ${\displaystyle G}$. Через ${\displaystyle Adj(v)}$ обозначим множество всех вершин графа, смежных с ${\displaystyle v}$. Предположим, что мы просмотрели граф в глубину, начав с некоторой произвольной вершины. Занумеруем все вершины графа в том порядке, в котором мы в них вошли, и каждой вершине ${\displaystyle v}$ припишем соответствующий номер ${\displaystyle n(v)}$. Если в вершину ${\displaystyle u}$ мы впервые попали из вершины ${\displaystyle v}$, то вершину ${\displaystyle u}$ будем называть потомком ${\displaystyle v}$, а ${\displaystyle v}$ — предком ${\displaystyle u}$. Множество всех потомков вершины ${\displaystyle v}$ обозначим через ${\displaystyle Ch(v)}$. Через ${\displaystyle Low(v)}$ обозначим минимальный номер среди всех вершин, смежных с ${\displaystyle v}$ и с теми вершинами, в которые мы пришли по пути, проходящем через ${\displaystyle v}$.

Ясно, что величину ${\displaystyle Low(v)}$ можно вычислить рекурсивно, непосредственно в процессе обхода в глубину: если в настоящий момент рассматривается вершина ${\displaystyle v}$, и из неё нельзя перейти в ещё не посещённую вершину (т.е. нужно вернуться к предку ${\displaystyle v}$, или прекратить обход, если ${\displaystyle v}$ — стартовая вершина), то для всех её потомков ${\displaystyle Low}$ уже посчитано, а значит, и для неё можно провести соответствующие вычисления по формуле

${\displaystyle Low(v)=\min \left\{\min _{x\in Ch(v)}Low(x),\min _{y\in Adj(v)/Ch(v)}n(y)\right\}.}$

Зная величину ${\displaystyle Low(v)}$ для всех вершин графа, можно однозначным образом определить все его шарниры согласно следующим двум правилам:

1. Стартовая вершина (т.е. та, с которой мы начали обход) является шарниром тогда и только тогда, когда у неё больше одного потомка.
2. Вершина ${\displaystyle v}$, отличная от стартовой, является шарниром тогда и только тогда, когда у неё есть потомок u такой, что ${\displaystyle Low(u)=n(v)}$.

В качестве примера рассмотрим применение описанного алгоритма к графу, изображённому на рисунке справа. Числа, которыми помечены вершины, соответствуют одному из возможных вариантов обхода в глубину. При таком порядке у каждой из вершин ровно один потомок, за исключением вершины 6, у которой потомков нет. Стартовая вершина 1 имеет единственного потомка, следовательно, шарниром она не является. Для остальных вершин вычислим значения интересующей нас функции:

${\displaystyle Low(6)=5,Low(5)=2,Low(4)=2,Low(3)=2,Low(2)=1}$.

У вершины 2 есть потомок 3, а у 5 потомок 6 — в обоих случаях выполнено искомое соотношение ${\displaystyle Low(u)=n(v)}$. Следовательно, 2 и 5 являются шарнирами. Других шарниров в этом графе нет.

• Компонента связности графа

• В. Е. Алексеев, В. А. Таланов. Графы и алгоритмы. Структуры данных. Модели вычислений. — М.: БИНОМ. Лаборатория знаний, 2006. — ISBN 5-94774-543-7.