–Į–Ņ–ĺ–Ĺ—Ā–ļ–į—Ź —ā–Ķ–ĺ—Ä–Ķ–ľ–į –ĺ –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–ľ —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ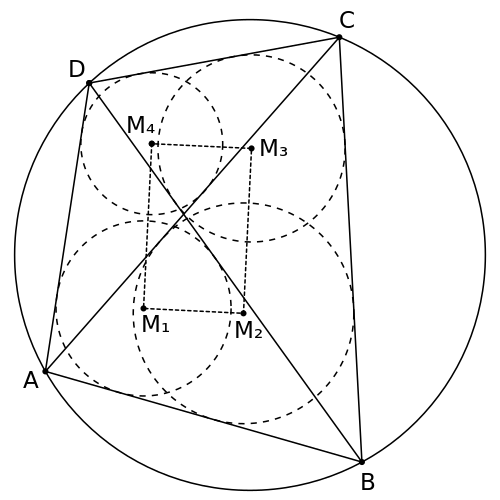 –Į–Ņ–ĺ–Ĺ—Ā–ļ–į—Ź —ā–Ķ–ĺ—Ä–Ķ–ľ–į –ĺ –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–ľ —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ —É—ā–≤–Ķ—Ä–∂–ī–į–Ķ—ā, —á—ā–ĺ —Ü–Ķ–Ĺ—ā—Ä—č –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–Ķ–Ļ, –≤–Ņ–ł—Ā–į–Ĺ–Ĺ—č—Ö –≤ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ—č–Ķ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł –≤–Ĺ—É—ā—Ä–ł –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–≥–ĺ –≤ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į, —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –≤–Ķ—Ä—ą–ł–Ĺ–į–ľ–ł –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į. –†–į–∑–Ī–ł–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–≥–ĺ —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ź–ľ–ł –ī–į—Ď—ā —á–Ķ—ā—č—Ä–Ķ –Ņ–Ķ—Ä–Ķ–ļ—Ä—č–≤–į—é—Č–ł—Ö –ī—Ä—É–≥ –ī—Ä—É–≥–į —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –ļ–į–∂–ī–į—Ź –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć —Ā–ĺ–∑–ī–į—Ď—ā –ī–≤–į —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į). –¶–Ķ–Ĺ—ā—Ä—č –≤–Ņ–ł—Ā–į–Ĺ–Ĺ—č—Ö –≤ —ć—ā–ł —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–Ķ–Ļ –ĺ–Ī—Ä–į–∑—É—é—ā –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ. –í —á–į—Ā—ā–Ĺ–ĺ—Ā—ā–ł, –Ņ—É—Ā—ā—Ć ‚Ė°ABCD ‚ÄĒ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ—č–Ļ –≤–Ņ–ł—Ā–į–Ĺ–Ĺ—č–Ļ —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ –ł –Ņ—É—Ā—ā—Ć M1, M2, M3, M4 ‚ÄĒ —Ü–Ķ–Ĺ—ā—Ä—č –≤–Ņ–ł—Ā–į–Ĺ–Ĺ—č—Ö –≤ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł ‚Ė≥ABD, ‚Ė≥ABC, ‚Ė≥BCD, ‚Ė≥ACD –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–Ķ–Ļ. –Ę–ĺ–≥–ī–į —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ, –ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–Ĺ—č–Ļ —Ü–Ķ–Ĺ—ā—Ä–į–ľ–ł M1, M2, M3, M4, —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–ľ. –Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ[1](–Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–ĺ–Ļ —É–≥–Ľ–į , –į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–ĺ–Ļ —É–≥–Ľ–į ) –ź–Ĺ–į–Ľ–ĺ–≥–ł—á–Ĺ–ĺ –Ņ–ĺ–Ľ—É—á–į–Ķ–ľ –ü–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ –≤–Ņ–ł—Ā–į–Ĺ–Ĺ—č–Ļ, –ł–ľ–Ķ–Ķ–ľ , –ĺ—ā–ļ—É–ī–į —Ā–Ľ–Ķ–ī—É–Ķ—ā, —á—ā–ĺ —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ —ā–ĺ–∂–Ķ –≤–Ņ–ł—Ā–į–Ĺ –≤ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć, —ā–į–ļ —á—ā–ĺ –Ņ–ĺ–Ľ—É—á–į–Ķ–ľ –ź–Ĺ–į–Ľ–ĺ–≥–ł—á–Ĺ–ĺ –Ņ–ĺ–Ľ—É—á–į–Ķ–ľ –ź —Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –Ę–Ķ–ľ –∂–Ķ —Ā–į–ľ—č–ľ —Ā–Ņ–ĺ—Ā–ĺ–Ī–ĺ–ľ –ī–ĺ–ļ–į–∑—č–≤–į–Ķ–ľ –ī–Ľ—Ź –ī—Ä—É–≥–ł—Ö —É–≥–Ľ–ĺ–≤. –ü–ĺ–Ľ—É—á–į–Ķ–ľ, —á—ā–ĺ –≤—Ā–Ķ —á–Ķ—ā—č—Ä–Ķ —É–≥–Ľ–į —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –Ņ—Ä—Ź–ľ—č–Ķ. –Ę–Ķ–ĺ—Ä–Ķ–ľ–į –ī–ĺ–ļ–į–∑–į–Ĺ–į –ó–į–ľ–Ķ—ā–ł–ľ, —á—ā–ĺ –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ —ć—ā–ĺ–Ļ —ā–Ķ–ĺ—Ä–Ķ–ľ—č –Ľ–Ķ–≥–ļ–ĺ –ĺ–Ī–ĺ–Ī—Č–į–Ķ—ā—Ā—Ź –ī–ĺ –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–į —Ź–Ņ–ĺ–Ĺ—Ā–ļ–ĺ–Ļ —ā–Ķ–ĺ—Ä–Ķ–ľ—č –ĺ –≤–Ņ–ł—Ā–į–Ĺ–Ĺ—č—Ö –ľ–Ĺ–ĺ–≥–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į—Ö (Japanese theorem for cyclic polygons). –ė–∑ —Ā–Ľ—É—á–į—Ź —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –Ĺ–Ķ–ľ–Ķ–ī–Ľ–Ķ–Ĺ–Ĺ–ĺ –≤—č—ā–Ķ–ļ–į–Ķ—ā –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ –ī–Ľ—Ź –ĺ–Ī—Č–Ķ–≥–ĺ –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–≥–ĺ –ľ–Ĺ–ĺ–≥–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į (–Ņ–ĺ –ł–Ĺ–ī—É–ļ—Ü–ł–ł –Ņ–ĺ —á–ł—Ā–Ľ—É —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤ –≤ —Ä–į–∑–Ī–ł–Ķ–Ĺ–ł–ł –ľ–Ĺ–ĺ–≥–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į).
–ó–į–ľ–Ķ—á–į–Ĺ–ł–Ķ 1–Ē–Ľ—Ź –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–≥–ĺ —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ź–Ņ–ĺ–Ĺ—Ā–ļ–į—Ź —ā–Ķ–ĺ—Ä–Ķ–ľ–į –ĺ –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–ľ —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ā–ĺ—Ā—ā–į–≤–Ĺ–ĺ–Ļ —á–į—Ā—ā—Ć—é –Ī–ĺ–Ľ–Ķ–Ķ —Ā–Ľ–ĺ–∂–Ĺ–ĺ–≥–ĺ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł—Ź:
–°–ľ. —ā–į–ļ–∂–Ķ
–õ–ł—ā–Ķ—Ä–į—ā—É—Ä–į
–°—Ā—č–Ľ–ļ–ł
|
Portal di Ensiklopedia Dunia

























