–Ē–ł—ć–ī—Ä–į–Ľ—Ć–Ĺ–į—Ź —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—Ź –≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ
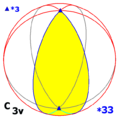
–Ē–ł—ć–ī—Ä–į–Ľ—Ć–Ĺ–į—Ź —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—Ź –≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ ‚ÄĒ —ć—ā–ĺ –ĺ–ī–Ĺ–į –ł–∑ —ā—Ä—Ď—Ö –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ—č—Ö –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–Ķ–Ļ —ā–ĺ—á–Ķ—á–Ĺ—č—Ö –≥—Ä—É–Ņ–Ņ –≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ł–ľ–Ķ—é—ā –≥—Ä—É–Ņ–Ņ—č —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł, —Ź–≤–Ľ—Ź—é—Č–ł–Ķ—Ā—Ź –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ—č–ľ–ł –ī–ł—ć–ī—Ä–į–Ľ—Ć–Ĺ—č–ľ–ł –≥—Ä—É–Ņ–Ņ–į–ľ–ł Dihn (–ī–Ľ—Ź n ‚Č• 2). –Ę–ł–Ņ—č–°—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā —ā—Ä–ł —ā–ł–Ņ–į –ī–ł—ć–ī—Ä–į–Ľ—Ć–Ĺ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ, –ļ–į–∂–ī–į—Ź –Ņ–ĺ–ļ–į–∑–į–Ĺ–į –Ĺ–ł–∂–Ķ –≤ —ā—Ä—Ď—Ö –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź—Ö: –Ĺ–ĺ—ā–į—Ü–ł—Ź –®—Ď–Ĺ—Ą–Ľ–ł—Ā–į, –Ĺ–ĺ—ā–į—Ü–ł—Ź –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į[–į–Ĺ–≥–Ľ.] –ł –ĺ—Ä–Ī–ł—Ą–ĺ–Ľ–ī–Ĺ–į—Ź –Ĺ–ĺ—ā–į—Ü–ł—Ź[–į–Ĺ–≥–Ľ.].
(–į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ–į—Ź –≥—Ä—É–Ņ–Ņ–į - Dihn).
(–į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ–į—Ź –≥—Ä—É–Ņ–Ņ–į - Dihn √ó Z2).
(–į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ–į—Ź –≥—Ä—É–Ņ–Ņ–į - Dih2n). –Ē–Ľ—Ź –∑–į–ī–į–Ĺ–Ĺ–ĺ–≥–ĺ n –≤—Ā–Ķ —ā—Ä–ł —ā–ł–Ņ–į –ł–ľ–Ķ—é—ā –≤—Ä–į—Č–į—ā–Ķ–Ľ—Ć–Ĺ—É—é —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—é –Ņ–ĺ—Ä—Ź–ī–ļ–į n –≤–ĺ–ļ—Ä—É–≥ –ĺ–ī–Ĺ–ĺ–Ļ –ĺ—Ā–ł (–≤—Ä–į—Č–Ķ–Ĺ–ł–Ķ –Ĺ–į —É–≥–ĺ–Ľ 360¬į/n –Ĺ–Ķ –ł–∑–ľ–Ķ–Ĺ—Ź–Ķ—ā –ĺ–Ī—ä–Ķ–ļ—ā), –ł n –≤—Ä–į—Č–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ļ –Ņ–ĺ—Ä—Ź–ī–ļ–į 2 –ī–Ľ—Ź –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—č—Ö –ĺ—Ā–Ķ–Ļ. –Ē–Ľ—Ź n = ‚ąě –ĺ–Ĺ–ł —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—ā —ā—Ä—Ď–ľ –≥—Ä—É–Ņ–Ņ–į–ľ –Ī–ĺ—Ä–ī—é—Ä–į. –ě–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ļ —É–ļ–į–∑–į–Ĺ—č –≤ –Ĺ–ĺ—ā–į—Ü–ł–ł –®—Ď–Ĺ—Ą–Ľ–ł—Ā–į, –≤ –ļ–≤–į–ī—Ä–į—ā–Ĺ—č—Ö —Ā–ļ–ĺ–Ī–ļ–į—Ö - –≤ –Ĺ–ĺ—ā–į—Ü–ł–ł –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į[–į–Ĺ–≥–Ľ.] –ł –≤ –ļ—Ä—É–≥–Ľ—č—Ö —Ā–ļ–ĺ–Ī–ļ–į—Ö - –≤ –ĺ—Ä–Ī–ł—Ą–ĺ–Ľ–ī–Ĺ–ĺ–Ļ –Ĺ–ĺ—ā–į—Ü–ł–ł[–į–Ĺ–≥–Ľ.]. –Ę–Ķ—Ä–ľ–ł–Ĺ ¬ę–≥–ĺ—Ä–ł–∑–ĺ–Ĺ—ā–į–Ľ—Ć–Ĺ—č–Ļ¬Ľ (h) –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź –Ņ–ĺ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—é –ļ –≤–Ķ—Ä—ā–ł–ļ–į–Ľ—Ć–Ĺ–ĺ–Ļ –ĺ—Ā–ł –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź. –í –ī–≤—É–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ (–Ĺ–į –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł) –≥—Ä—É–Ņ–Ņ–į —Ā–ł–ľ–Ķ—ā—Ä–ł–ł Dn –≤–ļ–Ľ—Ź—á–į–Ķ—ā –∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ–ĺ–Ķ –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł–Ķ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ņ—Ä—Ź–ľ—č—Ö. –ē—Ā–Ľ–ł –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā—Ć –≤–Ľ–ĺ–∂–Ķ–Ĺ–į –≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ, —ā–į–ļ–ł–Ķ –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł—Ź –ľ–ĺ–∂–Ĺ–ĺ —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—ā—Ć –Ľ–ł–Ī–ĺ –ļ–į–ļ —Ā—É–∂–Ķ–Ĺ–ł–Ķ –Ĺ–į –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā—Ć –∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł—Ź –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –≤–Ķ—Ä—ā–ł–ļ–į–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł, –Ľ–ł–Ī–ĺ –ļ–į–ļ —Ā—É–∂–Ķ–Ĺ–ł–Ķ –Ĺ–į –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā—Ć –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź –Ĺ–į 180¬į –≤–ĺ–ļ—Ä—É–≥ –ĺ—Ā–ł –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź. –í —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ –ī–≤–Ķ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –ĺ—ā–Ľ–ł—á–į—é—ā—Ā—Ź - –≥—Ä—É–Ņ–Ņ–į Dn —Ā–ĺ–ī–Ķ—Ä–∂–ł—ā —ā–ĺ–Ľ—Ć–ļ–ĺ –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź –ł –Ĺ–Ķ —Ā–ĺ–ī–Ķ—Ä–∂–ł—ā –∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ—č—Ö –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł–Ļ. –Ē—Ä—É–≥–į—Ź –≥—Ä—É–Ņ–Ņ–į - —Ü–ł–ļ–Ľ–ł—á–Ķ—Ā–ļ–į—Ź –ł–Ľ–ł –Ņ–ł—Ä–į–ľ–ł–ī–į–Ľ—Ć–Ĺ–į—Ź —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—Ź[–į–Ĺ–≥–Ľ.] Cnv —ā–ĺ–≥–ĺ –∂–Ķ –Ņ–ĺ—Ä—Ź–ī–ļ–į 2n. –í–ľ–Ķ—Ā—ā–Ķ —Ā –∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ķ–Ļ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł, –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ–ĺ–Ļ –ĺ—Ā–ł –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź –Ņ–ĺ—Ä—Ź–ī–ļ–į n, –ľ—č –ł–ľ–Ķ–Ķ–ľ Dnh, [n], (*22n). Dnd (–ł–Ľ–ł Dnv), [2n,2+], (2*n) –ł–ľ–Ķ–Ķ—ā –≤–Ķ—Ä—ā–ł–ļ–į–Ľ—Ć–Ĺ—č–Ķ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł—Ź, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–ł–Ķ –ľ–Ķ–∂–ī—É –≥–ĺ—Ä–ł–∑–ĺ–Ĺ—ā–į–Ľ—Ć–Ĺ—č–ľ–ł –ĺ—Ā—Ź–ľ–ł –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź, –į –Ĺ–Ķ —á–Ķ—Ä–Ķ–∑ –Ĺ–ł—Ö. –ö–į–ļ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā, –≤–Ķ—Ä—ā–ł–ļ–į–Ľ—Ć–Ĺ–į—Ź –ĺ—Ā—Ć —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ĺ—Ā—Ć—é –Ĺ–Ķ—Ā–ĺ–Ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź[–į–Ĺ–≥–Ľ.] –Ņ–ĺ—Ä—Ź–ī–ļ–į 2n. Dnh —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≥—É–Ņ–Ņ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–Ļ n-—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ—Ä–ł–∑–ľ—č, –į —ā–į–ļ–∂–Ķ –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–Ļ n-—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–Ļ –Ī–ł–Ņ–ł—Ä–į–ľ–ł–ī—č. Dnd —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≥—É–Ņ–Ņ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–Ļ n-—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–Ļ –į–Ĺ—ā–ł–Ņ—Ä–ł–∑–ľ—č, –į —ā–į–ļ–∂–Ķ –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–≥–ĺ n-—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–į–Ņ–Ķ—Ü–ĺ—ć–ī—Ä–į. Dn —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≥—É–Ņ–Ņ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł —á–į—Ā—ā–ł—á–Ĺ–ĺ –Ņ–ĺ–≤—Ď—Ä–Ĺ–Ļ—ā–ĺ–Ļ –Ņ—Ä–ł–∑–ľ—č. –°–Ľ—É—á–į–Ļ n = 1 –Ĺ–Ķ –≤–ļ–Ľ—é—á—Ď–Ĺ, –Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É —ā—Ä–ł —ā–ł–Ņ–į —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł —Ä–į–≤–Ĺ—č —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ:
–Ē–Ľ—Ź n = 2 –Ĺ–Ķ—ā –≥–Ľ–į–≤–Ĺ–ĺ–Ļ –ĺ—Ā–ł –ł –ī–≤—É—Ö –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ—č—Ö, –į –Ķ—Ā—ā—Ć —ā—Ä–ł —Ä–į–≤–Ĺ–ĺ–Ņ—Ä–į–≤–Ĺ—č–Ķ –ĺ—Ā–ł.
–°–ł–ľ–ľ–Ķ—ā—Ä–ł—Ź –ł–ľ–Ķ–Ķ—ā —ā—Ä–ł –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—č–Ķ –ĺ—Ā–ł –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ņ–ĺ—Ä—Ź–ī–ļ–į. –ě–Ĺ–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≥—Ä—É–Ņ–Ņ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł –ļ—É–Ī–ĺ–ł–ī–į —Ā –Ī—É–ļ–≤–ĺ–Ļ S, –Ĺ–į–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –Ĺ–į –ī–≤—É—Ö –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ—č—Ö –≥—Ä–į–Ĺ—Ź—Ö —Ā —ā–ĺ–Ļ –∂–Ķ –ĺ—Ä–ł–Ķ–Ĺ—ā–į—Ü–ł–Ķ–Ļ.
Td; –Ņ—É—ā—Ď–ľ —Ä–į—Ā—ā—Ź–∂–Ķ–Ĺ–ł—Ź –ľ—č —É–ľ–Ķ–Ĺ—Ć—ą–į–Ķ–ľ —Ā–ł–ľ–Ķ—ā—Ä–ł—é). –ü–ĺ–ī–≥—Ä—É–Ņ–Ņ—č
–Ē–Ľ—Ź Dnh, [n,2], (*22n) –Ņ–ĺ—Ä—Ź–ī–ļ–į 4n
–Ē–Ľ—Ź Dnd, [2n,2+], (2*n) –Ņ–ĺ—Ä—Ź–ī–ļ–į 4n
Dnd —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ā–į–ļ–∂–Ķ –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ—č D2nh. –ü—Ä–ł–ľ–Ķ—Ä—č
Dnh, [2,n], (*22n):
D5h, [2,5], (*225):
D4d, [8,2+], (2*4):
D5d, [10,2+], (2*5):
D17d, [34,2+], (2*17):
–°–ľ–ĺ—ā—Ä–ł—ā–Ķ —ā–į–ļ–∂–Ķ
–ü—Ä–ł–ľ–Ķ—á–į–Ĺ–ł—Ź–õ–ł—ā–Ķ—Ä–į—ā—É—Ä–į
–°—Ā—č–Ľ–ļ–ł
|
||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia