Algorithm

This article does not have any sources. You can help Wikipedia by finding good sources, and adding them. (June 2024)

An algorithm is a list of steps that can be followed to solve a problem using a limited number of steps. For example, a recipe is an algorithm to prepare a dish in a limited amount of time.

The words 'algorithm' and 'algorism' come from the name of a Persian mathematician called Al-Khwārizmī (Persian: خوارزمی, c. 780–850).

In computing, an algorithm is a precise list of operations that could be done by a Turing machine. For the purpose of computing, algorithms are written in pseudocode, flow charts, or programming languages.

There is usually more than one way to solve a problem. There may be many different recipes to make a certain dish which looks different but ends up tasting the same when all is said and done. The same is true for algorithms. However, some of these ways will be better than others. If a recipe needs lots of complicated ingredients that you do not have, it is not as a good as a simple recipe. When we look at algorithms as a way of solving problems, often we want to know how long it would take a computer to solve the problem using a particular algorithm. When we write algorithms, we like our algorithm to take the least amount of time so that we can solve our problem as quickly as possible.

In cooking, some recipes are more difficult to do than others, because they take more time to finish or have more things to keep track of. It is the same for algorithms, and algorithms are better when they are easier for the computer to do. The thing that measures the difficulty of an algorithm is called complexity. When we ask how complex an algorithm is, often we want to know how long it will take a computer to solve the problem we want it to solve.

This is an example of an algorithm for sorting cards with colors on them into piles of the same color:

1. Pick up all of the cards.
2. Pick a card from your hand and look at the color of the card.
3. If there is already a pile of cards of that color, put this card on that pile.
4. If there is no pile of cards of that color, make a new pile of just this card color.
5. If there is still a card in your hand, go back to the second step.
6. If there is not still a card in your hand, then the cards are sorted. You are done.

These are examples of algorithms for sorting a stack of cards with many different numbers, so that the numbers are in order.

Players start with a stack of cards that have not been sorted.

This algorithm goes through the stack of cards, one card at a time. This card is compared to the next card in the stack. Please note that this position only changes in step 6. This algorithm is called bubble sort. It is slow.

1. If the stack of cards is empty, or it only contains one card, it is sorted; you are done.
2. Take the stack of cards. Look at the first card (the top) of the stack.
3. The card you are looking at is card A. The position where card A currently, is in stack P.
4. If there are no more cards in the stack after card A, go to step 8.
5. The next card in the stack is card B.
6. If card B has a lower number than card A, swap the positions of cards A and B. Remember you did this. When you swap cards, do not change the position P.
7. If there is another card in the stack after position P, look at it; go back to step 3.
8. If you did not swap the position of any cards in the last run, you are done; the stack of cards is sorted.
9. Otherwise go back to step 2.

Let us take a stack of the cards with the numbers "5 1 4 2 8", and sort it from smallest number to biggest one using this algorithm. In each step, the algorithm compares the elements written in bold. The top of the stack of cards is on the left-hand side.

First pass:
( 5 1 4 2 8 ) ${\displaystyle \to }$ ( 1 5 4 2 8 ) Here, the algorithm compares the first two elements, and swaps them.
( 1 5 4 2 8 ) ${\displaystyle \to }$ ( 1 4 5 2 8 )
( 1 4 5 2 8 ) ${\displaystyle \to }$ ( 1 4 2 5 8 )
( 1 4 2 5 8 ) ${\displaystyle \to }$ ( 1 4 2 5 8 ) These elements are already in order, so the algorithm does not swap them.
Second pass:
( 1 4 2 5 8 ) ${\displaystyle \to }$ ( 1 4 2 5 8 )
( 1 4 2 5 8 ) ${\displaystyle \to }$ ( 1 2 4 5 8 )
( 1 2 4 5 8 ) ${\displaystyle \to }$ ( 1 2 4 5 8 )
( 1 2 4 5 8 ) ${\displaystyle \to }$ ( 1 2 4 5 8 )
Now, the stack of cards is already sorted, but our algorithm does not know this. The algorithm needs one whole pass without any swap to know it is sorted.
Third pass:
( 1 2 4 5 8 ) ${\displaystyle \to }$ ( 1 2 4 5 8 )
( 1 2 4 5 8 ) ${\displaystyle \to }$ ( 1 2 4 5 8 )
( 1 2 4 5 8 ) ${\displaystyle \to }$ ( 1 2 4 5 8 )
( 1 2 4 5 8 ) ${\displaystyle \to }$ ( 1 2 4 5 8 )
Finally, the array is sorted, and the algorithm can stop.

This is an easy-to-understand algorithm for sorting. Computer scientists called it Bubble sort, because smaller elements will rise to the top, changing their position in each run. Unfortunately, the algorithm is not very good, because it needs a long time (many passes through the stack of cards) to sort it.

This algorithm uses another idea. Sometimes solving a problem is difficult, but the problem can be changed so it is made of simpler problems that are easier to solve. This is called recursion. It is more difficult to understand than the first example, but it will give a better algorithm.

1. If the stack has no cards in it, or it only has one card, it is sorted, and you are done.
2. Split the stack of cards into two halves of about the same size. If there is an odd number of cards, one of the two stacks will have one card more than the other.
3. Sort each of the two stacks using this algorithm (For each stack, start at item 1 of this list.)
4. Merge the two sorted stacks together, as described below.
5. The result is a sorted stack of cards. You are done.

This works with two stacks of cards. One of them is called A, the other is called B. There is a third stack that is empty at the start, called C. At the end, it will contain the result.

1. If either stack A or stack B is empty, put all the cards of the stack that is not empty on top of stack C; you are done, stack C is the result of the merge. (Note: take the whole stack, and put it on stack C; doing it card-by-card will change the order and will not work as it should.)
2. Look at the top cards of stack A and stack B. Put the one with the lower number on top of stack C. If stack C had no cards in it, it will now have one card.
3. If either stack A or stack B has cards left, go back to step 1 to sort them.

John von Neumann developed this algorithm in 1945. He did not call it Sorting by numbers, he called it Mergesort. It is a very good algorithm for sorting, compared to others.

Th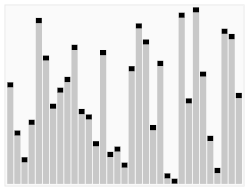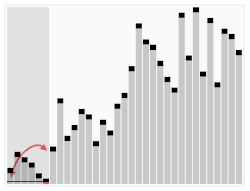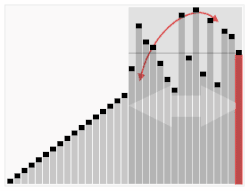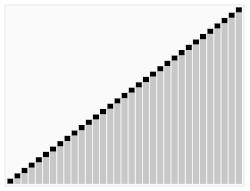e first algorithm takes much longer to sort the cards than the second, but it can be improved (made better). Looking at bubble sort, it can be noticed that cards with high numbers move from the top of the stack quite quickly, but cards with low numbers at the bottom of the stack take a long time to rise (move to the top). To improve the first algorithm here is the idea:

Rather than comparing two cards that are next to each other, at the start a 'special' card is picked. All the other cards are then compared to this card.

1. We start out with a stack A. There will be two other stacks B and C, which will be created later.
2. If stack A has no cards, or it only has one card, we are done sorting.
3. A card is picked from stack A, if possible at random. This is called a pivot.
4. All the remaining cards of stack A are compared to this pivot. Cards with a smaller number go to stack B, those with an equal or bigger number go to stack C.
5. If there are any cards in stacks B or C, these stacks need to be sorted with the same algorithm (Start at pos 1 of this list for both stack B and stack C in turn.)
6. Done. The sorted stack of cards first has the sorted stack B, then the pivot, and then the sorted stack C.

This algorithm was developed by C. A. R. Hoare in 1960. It is one of most widely used algorithms for sorting today. It is called Quicksort.

If players have cards with colors and numbers on them, they can sort them by color and number if they do the "sorting by colors" algorithm, then do the "sorting by numbers" algorithm to each colored stack, then put the stacks together.

The sorting-by-numbers algorithms are more difficult to do than the sorting-by-colors algorithm, because they may have to do the steps again many times. One would say that sorting by numbers is more complex.

• The Euclidean algorithm was found over 2000 years ago. It is able to find the greatest common divisor of two numbers.
• Numerical analysis

Wikimedia Commons has media related to Algorithms.

• Algorithm -Citizendium