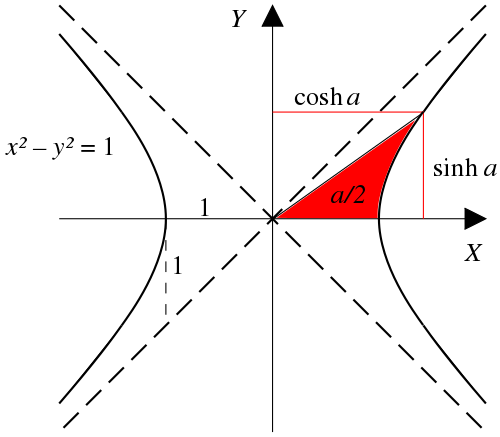
In mathematics , hyperbolic functions are analogues of the ordinary trigonometric functions , but defined for the unit hyperbola rather than on the unit circle : just as the points (cos t , sin t ) form a circle with a unit radius , the points (cosh t , sinh t ) form the right half of the hyperbola .
Hyperbolic functions occur in the calculations of angles and distances in hyperbolic geometry . They also occur in the solutions of many linear differential equations , cubic equations , and Laplace's equation in Cartesian coordinates . Laplace's equations are important in many areas of physics .
The basic hyperbolic functions are:[ 1] [ 2]
hyperbolic sine "sinh" (),[ 3] hyperbolic cosine "cosh" (),[ 4] from which are derived:[ 5]
hyperbolic tangent "tanh" (),[ 6] hyperbolic cosecant "csch" or "cosech" ([ 4] hyperbolic secant "sech" (),[ 7] hyperbolic cotangent "coth" (),[ 8] [ 9] corresponding to the derived trigonometric functions.
The inverse hyperbolic functions are:[ 1]
area hyperbolic sine "arsinh" (also denoted "sinh−1 ", "asinh" or sometimes "arcsinh")[ 10] [ 11] area hyperbolic cosine "arcosh" (also denoted "cosh−1 ", "acosh" or sometimes "arccosh"and so on. A ray through the unit hyperbola x 2 − y 2 = 1(cosh a , sinh a ) , where a is twice the area between the ray, the hyperbola, and the x -axis. For points on the hyperbola below the x -axis, the area is considered negative (see animated version with comparison with the trigonometric (circular) functions). The hyperbolic functions take a real argument called a hyperbolic angle . The size of a hyperbolic angle is twice the area of its hyperbolic sector . The hyperbolic functions may be defined in terms of the legs of a right triangle covering this sector.
Hyperbolic functions were introduced in the 1760s independently by Vincenzo Riccati and Johann Heinrich Lambert .[ 12]
Definitions
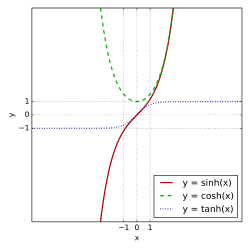
sinh , cosh and tanh csch , sech and coth There are various equivalent ways to define the hyperbolic functions.
Exponential definitions
sinh x is half the difference of ex e −x cosh x is the average of ex e −x In terms of the exponential function :[ 2] [ 5]
Hyperbolic sine: the odd part of the exponential function, that is
sinh
x
=
e
x
−
e
−
x
2
=
e
2
x
−
1
2
e
x
=
1
−
e
−
2
x
2
e
−
x
.
{\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}={\frac {e^{2x}-1}{2e^{x}}}={\frac {1-e^{-2x}}{2e^{-x}}}.}
Hyperbolic cosine: the even part of the exponential function, that is
cosh
x
=
e
x
+
e
−
x
2
=
e
2
x
+
1
2
e
x
=
1
+
e
−
2
x
2
e
−
x
.
{\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}={\frac {e^{2x}+1}{2e^{x}}}={\frac {1+e^{-2x}}{2e^{-x}}}.}
Hyperbolic tangent:
tanh
x
=
sinh
x
cosh
x
=
e
x
−
e
−
x
e
x
+
e
−
x
=
e
2
x
−
1
e
2
x
+
1
{\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}}
Hyperbolic cotangent: for x ≠ 0
coth
x
=
cosh
x
sinh
x
=
e
x
+
e
−
x
e
x
−
e
−
x
=
e
2
x
+
1
e
2
x
−
1
{\displaystyle \coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={\frac {e^{2x}+1}{e^{2x}-1}}}
Hyperbolic secant:
sech
x
=
1
cosh
x
=
2
e
x
+
e
−
x
=
2
e
x
e
2
x
+
1
{\displaystyle \operatorname {sech} x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}={\frac {2e^{x}}{e^{2x}+1}}}
Hyperbolic cosecant: for x ≠ 0
csch
x
=
1
sinh
x
=
2
e
x
−
e
−
x
=
2
e
x
e
2
x
−
1
{\displaystyle \operatorname {csch} x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}={\frac {2e^{x}}{e^{2x}-1}}}
Useful relations
The hyperbolic functions satisfy many identities, all of them similar in form to the trigonometric identities .
Odd and even functions:
sinh
(
−
x
)
=
−
sinh
x
cosh
(
−
x
)
=
cosh
x
{\displaystyle {\begin{aligned}\sinh(-x)&=-\sinh x\\\cosh(-x)&=\cosh x\end{aligned}}}
Hence:
tanh
(
−
x
)
=
−
tanh
x
coth
(
−
x
)
=
−
coth
x
sech
(
−
x
)
=
sech
x
csch
(
−
x
)
=
−
csch
x
{\displaystyle {\begin{aligned}\tanh(-x)&=-\tanh x\\\coth(-x)&=-\coth x\\\operatorname {sech} (-x)&=\operatorname {sech} x\\\operatorname {csch} (-x)&=-\operatorname {csch} x\end{aligned}}}
Thus, cosh x and sech x are even functions ; the others are odd functions .
arsech
x
=
arcosh
(
1
x
)
arcsch
x
=
arsinh
(
1
x
)
arcoth
x
=
artanh
(
1
x
)
{\displaystyle {\begin{aligned}\operatorname {arsech} x&=\operatorname {arcosh} \left({\frac {1}{x}}\right)\\\operatorname {arcsch} x&=\operatorname {arsinh} \left({\frac {1}{x}}\right)\\\operatorname {arcoth} x&=\operatorname {artanh} \left({\frac {1}{x}}\right)\end{aligned}}}
Hyperbolic sine and cosine satisfy:
cosh
x
+
sinh
x
=
e
x
cosh
x
−
sinh
x
=
e
−
x
cosh
2
x
−
sinh
2
x
=
1
{\displaystyle {\begin{aligned}\cosh x+\sinh x&=e^{x}\\\cosh x-\sinh x&=e^{-x}\\\cosh ^{2}x-\sinh ^{2}x&=1\end{aligned}}}
the last of which is similar to the Pythagorean trigonometric identity .
One also has
sech
2
x
=
1
−
tanh
2
x
csch
2
x
=
coth
2
x
−
1
{\displaystyle {\begin{aligned}\operatorname {sech} ^{2}x&=1-\tanh ^{2}x\\\operatorname {csch} ^{2}x&=\coth ^{2}x-1\end{aligned}}}
for the other functions.
Comparison with circular functions
Circle and hyperbola tangent at (1,1) display geometry of circular functions in terms of circular sector area u and hyperbolic functions depending on hyperbolic sector area u . The hyperbolic functions represent an expansion of trigonometry beyond the functions defined on unit circle. Both types depend on one argument , either circular angle or hyperbolic angle .
Since the area of a circular sector with radius r and angle u (in radians) is r 2 u /2, it will be equal to u when r = √2 . In the diagram, such a circle is tangent to the hyperbola xy = 1 at (1,1). The yellow sector depicts an area and angle magnitude. Similarly, the yellow and red sectors together depict an area and hyperbolic angle magnitude .
The legs of the two right triangles with hypotenuse on the ray defining the angles are of length
2
{\displaystyle {\sqrt {2}}}
Relationship to the exponential function
The decomposition of the exponential function in its even and odd parts gives the identities
e
x
=
cosh
x
+
sinh
x
,
{\displaystyle e^{x}=\cosh x+\sinh x,}
and
e
−
x
=
cosh
x
−
sinh
x
.
{\displaystyle e^{-x}=\cosh x-\sinh x.}
The first one is analogous to Euler's formula
e
i
x
=
cos
x
+
i
sin
x
.
{\displaystyle e^{ix}=\cos x+i\sin x.}
Additionally,
e
x
=
1
+
tanh
x
1
−
tanh
x
=
1
+
tanh
x
2
1
−
tanh
x
2
{\displaystyle e^{x}={\sqrt {\frac {1+\tanh x}{1-\tanh x}}}={\frac {1+\tanh {\frac {x}{2}}}{1-\tanh {\frac {x}{2}}}}}
Related pages
References
↑ 1.0 1.1 "Comprehensive List of Algebra Symbols" . Math Vault . 2020-03-25. Retrieved 2020-08-29 .↑ 2.0 2.1 Weisstein, Eric W. "Hyperbolic Functions" . mathworld.wolfram.com . Retrieved 2020-08-29 . ↑ (1999) Collins Concise Dictionary , 4th edition, HarperCollins, Glasgow, ISBN 0 00 472257 4 , p. 1386
↑ 4.0 4.1 Collins Concise Dictionary , p. 328↑ 5.0 5.1 "Hyperbolic Functions" . www.mathsisfun.com . Retrieved 2020-08-29 .↑ Collins Concise Dictionary , p. 1520↑ Collins Concise Dictionary , p. 1340↑ Collins Concise Dictionary , p. 329↑ tanh ↑ Woodhouse, N. M. J. (2003), Special Relativity , London: Springer, p. 71, ISBN 978-1-85233-426-0 ↑ Abramowitz, Milton ; Stegun, Irene A. , eds. (1972), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables Dover Publications , ISBN 978-0-486-61272-0 ↑ Robert E. Bradley, Lawrence A. D'Antonio, Charles Edward Sandifer. Euler at 300: an appreciation. Mathematical Association of America, 2007. Page 100.
Other websites