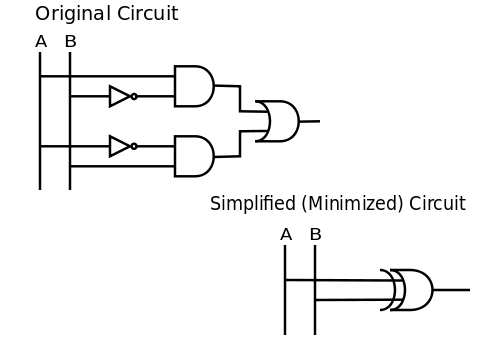
–ú–ł–Ĺ–ł–ľ–į–Ľ–ł–∑–į—Ü–ł—ė–į –ļ–ĺ–Ľ–į–£ –Ď—É–Ľ–ĺ–≤–ĺ—ė –į–Ľ–≥–Ķ–Ī—Ä–ł, –ľ–ł–Ĺ–ł–ľ–į–Ľ–ł–∑–į—Ü–ł—ė–į –ļ–ĺ–Ľ–į (—Ā—Ä–Ķ—õ–Ķ —Ā–Ķ –ł –ł–∑—Ä–į–∑ ‚Äě–ľ–ł–Ĺ–ł–ľ–ł–∑–į—Ü–ł—ė–į‚Äú) —ė–Ķ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ –ī–ĺ–Ī–ł—ė–į—ö–į –Ĺ–į—ė–ľ–į—ö–Ķ–≥ –Ľ–ĺ–≥–ł—á–ļ–ĺ–≥ –ļ–ĺ–Ľ–į (–Ď—É–Ľ–ĺ–≤–į –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł—ė–į) –ļ–ĺ—ė–Ķ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—ô–į –ī–į—ā—É –Ī—É–Ľ–ĺ–≤—É —Ą—É–Ĺ–ļ—Ü–ł—ė—É –ł–Ľ–ł —ā–į–Ī–Ľ–ł—Ü—É –ł—Ā—ā–ł–Ĺ–ł—ā–ĺ—Ā—ā–ł. –ě–Ņ—ą—ā–ł –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ –ľ–ł–Ĺ–ł–ľ–į–Ľ–ł–∑–į—Ü–ł—ė–Ķ –ļ–ĺ–Ľ–į —ė–Ķ —Ä–į—á—É–Ĺ—Ā–ļ–ł —ā–Ķ–∂–į–ļ, –į–Ľ–ł –Ņ–ĺ—Ā—ā–ĺ—ė–Ķ –Ķ—Ą–ł–ļ–į—Ā–Ĺ–Ķ —Ö–Ķ—É—Ä–ł—Ā—ā–ł–ļ–Ķ –ļ–į–ĺ —ą—ā–ĺ —Ā—É –ö–į—Ä–Ĺ–ĺ–ĺ–≤–Ķ –ļ–į—Ä—ā–Ķ –ł –ö–≤–į—ė–Ĺ‚Äď–ú–į–ļ–Ľ–į—Ā–ļ–ł—ė–Ķ–≤ –į–Ľ–≥–ĺ—Ä–ł—ā–į–ľ –ļ–ĺ—ė–Ķ –ĺ–Ľ–į–ļ—ą–į–≤–į—ė—É –Ņ—Ä–ĺ—Ü–Ķ—Ā. –°–≤—Ä—Ö–į–ü—Ä–ĺ–Ī–Ľ–Ķ–ľ —Ā–į –ļ–ĺ–ľ–Ņ–Ľ–ł–ļ–ĺ–≤–į–Ĺ–ł–ľ –ļ–ĺ–Ľ–ĺ–ľ (—ā—ė. –ļ–ĺ–Ľ–ĺ–ľ —Ā–į –ľ–Ĺ–ĺ–≥–ĺ –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ–į—ā–į , –ļ–į–ĺ —Ā—ā–ĺ —Ā—É –Ľ–ĺ–≥–ł—á–ļ–į –≤—Ä–į—ā–į –ļ–ĺ—ė–į –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—ô–į—ė—É –Ķ–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ—Ā–ļ–ł —Ā–ļ–Ľ–ĺ–Ņ –ļ–ĺ—ė–ł —Ā–Ľ–ł–∂–ł –∑–į –ĺ—Ā—ā–≤–į—Ä–Ķ—ö–Ķ –Ľ–ĺ–≥–ł—á–ļ–Ķ –ĺ–Ņ–Ķ—Ä–į—Ü–ł—ė–Ķ) —Ā–į—Ā—ā–ĺ—ė–ł —Ā–Ķ —É —ā–ĺ–ľ–Ķ –ī–į –∑–į—É–∑–ł–ľ–į —Ą–ł–∑–ł—á–ļ–ł –Ņ—Ä–ĺ—Ā—ā–ĺ—Ä –∑–į —ö–Ķ–≥–ĺ–≤–ĺ —Ā–Ņ—Ä–ĺ–≤–ĺ—í–Ķ—ö–Ķ –ł —ą—ā–ĺ —Ā–Ķ –Ņ–ĺ—ā—Ä–ĺ—ą–ł –≤—Ä–Ķ–ľ–Ķ –ł –Ĺ–ĺ–≤–į—Ü –∑–į —ö–Ķ–≥–ĺ–≤—É –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī—ö—É. –ú–ł–ľ–ł–ľ–ł–∑–į—Ü–ł—ė–į –ļ–ĺ–Ľ–į –ľ–ĺ–∂–Ķ –Ī–ł—ā–ł —ė–Ķ–ī–į–Ĺ –ĺ–Ī–Ľ–ł–ļ –Ľ–ĺ–≥–ł—á–ļ–Ķ –ĺ–Ņ—ā–ł–ľ–ł–∑–į—Ü–ł—ė–Ķ, –ļ–ĺ—ė–ł —Ā–Ķ –ļ–ĺ—Ä–ł—Ā—ā–ł –ī–į –Ī–ł —Ā–Ķ —Ā–ľ–į—ö–ł–Ľ–ĺ –Ņ–ĺ–ī—Ä—É—á—ė–Ķ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–Ķ –Ľ–ĺ–≥–ł–ļ–Ķ —É –ł–Ĺ—ā–Ķ–≥—Ä–ł—Ā–į–Ĺ–ł–ľ –ļ–ĺ–Ľ–ł–ľ–į. –ü—Ä–ł–ľ–Ķ—Ä–ė–į–ļ–ĺ –Ņ–ĺ—Ā—ā–ĺ—ė–ł –ľ–Ĺ–ĺ–≥–ĺ –Ĺ–į—á–ł–Ĺ–į –ī–į —Ā–Ķ –ľ–ł–Ĺ–ł–ľ–į–Ľ–ł–∑—É—ė–Ķ (—Ā–ľ–į—ö–ł) –ļ–ĺ–Ľ–ĺ, –ĺ–≤–ĺ —ė–Ķ –Ņ—Ä–ł–ľ–Ķ—Ä –ļ–ĺ—ė–ł –ľ–ł–Ĺ–ł–ľ–į–Ľ–ł–∑—É—ė–Ķ (–ł–Ľ–ł –Ņ–ĺ—ė–Ķ–ī–Ĺ–ĺ—Ā—ā–į–≤—ô—É—ė–Ķ) –Ī—É–Ľ–ĺ–≤—É —Ą—É–Ĺ–ļ—Ü–ł—ė—É. –Ę—Ä–Ķ–Ī–į –ł–ľ–į—ā–ł –Ĺ–į —É–ľ—É –ī–į —ė–Ķ –Ď—É–Ľ–ĺ–≤–į —Ą—É–Ĺ–ļ—Ü–ł—ė–į, –ł–∑–≤–Ķ–ī–Ĺ–į –Ņ–ĺ–ľ–ĺ—õ—É –ļ–ĺ–Ľ–į, —É –ī–ł—Ä–Ķ–ļ—ā–Ĺ–ĺ—ė –≤–Ķ–∑–ł —Ā–į –į–Ľ–≥–Ķ–Ī–į—Ä—Ā–ļ–ł–ľ –ł–∑—Ä–į–∑–ĺ–ľ –ł–∑ –ļ–ĺ—ė–Ķ–≥ —Ā–Ķ —Ä–Ķ–į–Ľ–ł–∑—É—ė–Ķ —Ą—É–Ĺ–ļ—Ü–ł—ė–į. –†–į–∑–ľ–ĺ—ā—Ä–ł–ľ–ĺ –ļ–ĺ–Ľ–ĺ –ļ–ĺ—ė–Ķ —Ā–Ķ –ļ–ĺ—Ä–ł—Ā—ā–ł –ī–į –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł . –ē–≤–ł–ī–Ķ–Ĺ—ā–Ĺ–ĺ —ė–Ķ –ī–į —Ā—É —É –ĺ–≤–ĺ–ľ –ļ–ĺ–Ľ—É —É–Ņ–ĺ—ā—Ä–Ķ–Ī—ô–Ķ–Ĺ–Ķ –ī–≤–Ķ –Ĺ–Ķ–≥–į—Ü–ł—ė–Ķ , –ī–≤–Ķ –ļ–ĺ–Ĺ—ė—É–Ĺ–ļ—Ü–ł—ė–Ķ –ł –ī–ł—Ā—ė—É–Ĺ–ļ—Ü–ł—ė–į. –Ę–ĺ –∑–Ĺ–į—á–ł –ī–į —Ā—É –∑–į –ł–∑–≥—Ä–į–ī—ö—É –ļ–ĺ–Ľ–į –Ņ–ĺ—ā—Ä–Ķ–Ī–Ĺ–ĺ –ī–≤–į –ł–Ĺ–≤–Ķ—Ä—ā–ĺ—Ä–į , –ī–≤–ĺ—ė–Ķ –ė –≤—Ä–į—ā–į –ł –ė–õ–ė –≤—Ä–į—ā–į. –ö–ĺ–Ľ–ĺ —Ā–Ķ –ľ–ĺ–∂–Ķ –Ņ–ĺ—ė–Ķ–ī–Ĺ–ĺ—Ā—ā–į–≤–ł—ā–ł –Ņ—Ä–ł–ľ–Ķ–Ĺ–ĺ–ľ –Ľ–ĺ–≥–ł—á–ļ–ł—Ö –ł–ī–Ķ–Ĺ—ā–ł—ā–Ķ—ā–į –ł–Ľ–ł –Ņ–ĺ–ľ–ĺ—õ—É –ł–Ĺ—ā—É–ł—Ü–ł—ė–Ķ. –ü–ĺ—ą—ā–ĺ —Ā–Ķ —É –Ņ—Ä–ł–ľ–Ķ—Ä—É –Ĺ–į–≤–ĺ–ī–ł –ī–į —ė–Ķ –ź —ā–į—á–Ĺ–ĺ –ļ–į–ī–į —ė–Ķ –Ď –Ĺ–Ķ—ā–į—á–Ĺ–ĺ –ł–Ľ–ł –ĺ–Ī—Ä–Ĺ—É—ā–ĺ, –ľ–ĺ–∂–Ķ —Ā–Ķ –∑–į–ļ—ô—É—á–ł—ā–ł –ī–į –ĺ–≤–ĺ —ė–Ķ–ī–Ĺ–ĺ—Ā—ā–į–≤–Ĺ–ĺ –∑–Ĺ–į—á–ł . –£ –ł–∑—Ä–į–∑–ł–ľ–į –Ľ–ĺ–≥–ł—á–ļ–ł—Ö –≤—Ä–į—ā–į, –Ĺ–Ķ—ė–Ķ–ī–Ĺ–į–ļ–ĺ—Ā—ā —ė–Ķ–ī–Ĺ–ĺ—Ā—ā–į–≤–Ĺ–ĺ –∑–Ĺ–į—á–ł –ē–ö–°–ė–õ–ė –≤—Ä–į—ā–į (–Ķ–ļ—Ā–ļ–Ľ—É–∑–ł–≤–Ĺ–ĺ –ė–õ–ė). –ü—Ä–Ķ–ľ–į –Ę–ĺ–ľ–Ķ, . –Ę–į–ī–į —Ā—É –ī–≤–į –ļ–ĺ–Ľ–į, –Ņ—Ä–ł–ļ–į–∑–į–Ĺ–į –ł—Ā–Ņ–ĺ–ī, –Ķ–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ–į: –ė—Ā–Ņ—Ä–į–≤–Ĺ–ĺ—Ā—ā —Ä–Ķ–∑—É–Ľ—ā–į—ā–į –ľ–ĺ–∂–Ķ —Ā–Ķ –ī–ĺ–ī–į—ā–Ĺ–ĺ –Ņ—Ä–ĺ–≤–Ķ—Ä–ł—ā–ł –Ņ–ĺ–ľ–ĺ—õ—É —ā–į–Ī–Ľ–ł—Ü–Ķ –ł—Ā—ā–ł–Ĺ–ł—ā–ĺ—Ā—ā–ł. –õ–ł—ā–Ķ—Ä–į—ā—É—Ä–į
|
Portal di Ensiklopedia Dunia