Пресек (теорија скупова)

У математици, пресек (ијек. пресјек; означен са ∩) два скупа A и B је скуп који садржи све елементе скупа A који такође припадају скупу B (или, еквивалентно, сви елементи скупа B који такође припадају скупу A), и ниједан други елемент^[1].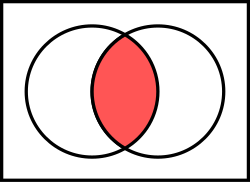

Формална дефиниција пресека два скупа A и B је скуп:

${\displaystyle A\cap B=\{x:x\in A\,\land \,x\in B\}}$

тј. x ∈A∩B ако и само ако

1. x ∈ A и
2. x ∈ B.

На пример:

• Пресек скупа {1, 2, 3} са скупом {2, 3, 4} је скуп {2, 3}.
• Број 9 није пресек скупа простих бројева {2, 3, 5, 7, 11, ...} и скупа непарних бројева {1, 3, 5, 7, 9, 11, ...}.^[2]

Уопште, може се рачунати пресек неколико скупова одједном. На пример, пресек скупова A, B, C, и D, је A ∩ B ∩ C ∩ D = A ∩ (B ∩ (C ∩ D)). Пресек скупова је асоцијативна операција па важи идентитет A ∩ (B ∩ C) = (A ∩ B) ∩ C.

Унутар универзума U може се дефинисати комплемент A^c скупа A као скуп свих елемената U који нису у A. Сада се пресек скупова A и B може записати као комплемент уније њихових комплемената, што следи из Де Морганових закона:

A ∩ B = (A^c ∪ B^c)^c.

• Унија (теорија скупова)
• Подскуп

• Weisstein, Eric W. "Intersection." From MathWorld-

Пресек на Викимедијиној остави.

Овај чланак везан за математику је клица. Можете допринети Википедији тако што ћете га проширити.

• п
• р
• у