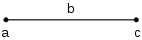கழித்தல் (கணிதம்)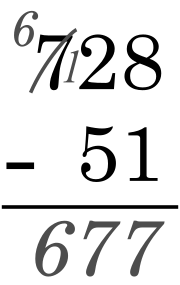

கழித்தல் என்பது, நான்கு அடிப்படையான கணிதச் செயல்களுள் ஒன்றாகும். இது கூட்டலுக்கு எதிர்மாறானது. கழித்தல் செயலானது, கழித்தல் (−) குறியினால் காட்டப்படுகின்றது. எடுத்துக்காட்டாக: 5 - 3 என்பது ஐந்திலிருந்து மூன்றைக் கழிப்பதைக் குறிக்கும். சமன் குறியீட்டுடன் இதற்கான விடை எழுதப்படுவது வழக்கம்.

எ.கா:

${\displaystyle 5-3=2.}$ இது, ஐந்து சய மூன்று சமன் இரண்டு என்று வாசிக்கப்படுகின்றது.

எதிர்ம எண்கள், பின்னங்கள், விகிதமுறா எண்கள், திசையன்கள், தசமங்கள், சார்புகள், அணிகள் போன்ற வெவ்வேறு விதமான பொருட்களைக் கொண்டு, இயற்கையான மற்றும் நுண்புலக் கணியங்களை நீக்குதல் மற்றும் குறைத்தலை, கழித்தல் என்னும் செயலி குறிக்கிறது.

கழித்தல் பல முக்கிய பண்புகளைக் கொண்டுள்ளது. இது பரிமாற்று விதிக்கு உட்பட்டதல்ல; அதாவது கழிக்கும் எண்களின் வரிசையை மாற்றினால் இறுதி விடையின் மதிப்பும் மாறிவிடும். கழித்தலுக்கு சேர்ப்புப் பண்பும் கிடையாது; அதாவது, செயலியை அமல்படுத்தும் வரிசை முறை மாற்றப்பட்டால் இறுதி விடை மாறிவிடும். எந்தவொரு எண்ணிலிருந்தும் எண் 0 ஐக் கழித்தால் மூல எண்ணில் மாற்றமிருக்காது. கூட்டல் (கணிதம்) மற்றும் பெருக்கல் (கணிதம்) தொடர்புடைய யூகிக்கக்கூடிய விதிகளை கழித்தல் நிறைவு செய்யும். இவ்விதிகள் அனைத்தையும் நிறுவ முடியும். முதலில் முழு எண்களைக் கொண்டு நிறுவி, பின்னர் மெய்யெண் மற்றும் அதற்கும் மேற்பட்டவற்றுக்கும் அவ்விதிகளைப் பொதுமைப்படுத்த முடியும். நுண்புல இயற்கணிதத்தில் இத்தகைய ஈருறுப்புச் செயலிகள் ஆய்வு செய்யப்படுகின்றன.

உறுப்புகளுக்கிடையே "−" குறியிட்டு கழித்தல் எழுதப்படுகிறது. விடை சமன் குறி கொண்டு எழுதப்படுகிறது.

எடுத்துக்காட்டுகள்:

${\displaystyle 2-1=1}$

${\displaystyle 4-2=2}$

${\displaystyle 6-3=3}$

${\displaystyle 4-6=-2}$

"−" குறியில்லாமலேயே கழித்தல் செயல் எழுதப்படும் சூழல்களும் உண்டு:

• ஒன்றன் கீழ் ஒன்றாக எழுதப்பட்ட இரு எண்களில் கீழுள்ள எண் சிவப்பு வண்ணத்தில் எழுதப்பட்டிருந்தால், இரண்டாவது எண் கழிக்கப்பட வேண்டிய எண் எனப் பொருள்படும். இரண்டாவது எண்ணுக்குக் கீழ் ஒரு கோடிடப்பட்டு, அதன்கீழ் விடை எழுதப்படுவது பொதுவழக்கமாக உள்ளது.

கழித்தலில், கழிக்கப்படும் எண் "கழிபடுவெண்" அல்லது "கழிக்கப்படுவெண்" (subtrahend) எனவும்,^[1][2] எந்த எண்ணிலிருந்து கழிக்கப்படுகிறதோ அவ்வெண் கழிமுதலெண் (minuend) எனவும்.^[1][2] கழிக்கக் கிடைக்கும் விடை வித்தியாசம் (difference) எனவும் அழைக்கப்படுகின்றன.^[1][2]

"கழித்தல்" என்பதற்கு இணையான ஆங்கில வார்த்தை "Subtraction" , இலத்தீன் மொழியின் வினைச்சொல் subtrahere என்பதிலிருந்து பெறப்பட்டது. இந்த இலத்தீன் சொல், sub ("from under") மற்றும் trahere ("to pull") என்ற இரு சொற்களிலிருந்து பெறப்பட்ட கூட்டுச்சொல்லாகும்.^[3][4]

படத்தில், b நீளமுள்ள ஒரு கோட்டுத்துண்டின் இடது முனை a என்றும் வலது முனை c என்றும் குறிப்பட்டுள்ளது.

• a இலிருந்து துவங்கி வலமாக b தொலைவு சென்றால் c ஐ அடையலாம்.

கூட்டலைப் பயன்படுத்தி இந்த வலப்புற நகர்வின் கணித மாதிரி:

a + b = c.

• c இலிருந்து துவங்கி, இடப்புறமாக b தொலைவு சென்றால் மீண்டும் a ஐச் சென்றடையலாம்.

கழித்தலைப் பயன்படுத்தி இந்த இடப்புற நகர்வின் கணித மாதிரி:

c − b = a.

படத்தில், 1, 2, 3 எண்கள் ஒரு நேர்கோட்டுத்துண்டில் குறிக்கப்பட்டுள்ளது.

• 3 இன் நிலையிலிருந்து 3 இன் நிலையிலேயே இருப்பதற்கு இடப்புறமாக நகரவேண்டியதே இல்லை. எனவே,

3 − 0 = 3.

• 3 இன் நிலையிலிருந்து 1 இன் நிலைக்குச் செல்ல இடப்புறமாக நகரவேண்டிய தொலைவு 2. எனவே,

3 − 2 = 1.

• 3 இன் நிலையிலிருந்து இடப்புறமாக மூன்று தொலைவு நகர்ந்தால் அடையும் நிலையைக் காட்ட இப்படம் போதுமானதாக இல்லை. அதற்கு கோட்டுத்துண்டினை இடப்புறமாக நீட்டிக்க வேண்டும்.

இயல் எண்களின் கழித்தலுக்கு, அனைத்து இயல் எண்களும் (0, 1, 2, 3, 4, 5, 6, ...) குறிக்கப்பட்ட எண்கோடு வேண்டும். அக்கோட்டில், 4 இலிருந்து நான்கு தொலைவு இடப்புறமாக நகர்ந்தால் 0 ஐ அடையலாம். அதாவது 4 − 4 = 0. ஆனால் 4 இலிருந்து 5 தொலைவு இடப்புறமாக நகர்வது இந்த இயல் எண்கோட்டில் இயலாது. (3 − 4)

இந்நகர்வுக்குத் தீர்வு முழுவெண் கோட்டில்தான் உண்டு.

3 − 4 = −1, ஒரு முழுவெண்.

எனவே இயல் எண்கள், கழித்தலுக்கு அடைவுப் பண்பு பெறவில்லை. இரு இயல் எண்களின் கழித்தல் விடை, இயல் எண்ணாகவே இருக்க வேண்டுமானால் கழிமுதலெண், கழிபடுவெண்ணைவிடப் பெரியதாக இருக்க வேண்டும்.

26 ஐ 11 இலிருந்து கழித்தல் முடியாது. இந்நிலையில் இருவித முடிவைக் கொள்ளலாம்:

1. 26 ஐ 11 இலிருந்து கழிக்க முடியாது; எனவே கழித்தல் இங்கு ஒரு பகுதிச் சார்பு ஆகிறது.
2. விடையை முழு எண்ணாகக் (எதிர்ம எண்) காணலாம். அதாவது,

11 - 26 = −15.

மெய்யெண்களின் கழித்தல், குறியிடப்பட்ட எண்களின் கூட்டலாக வரையறுக்கப்படுகிறது. ஒரு மெய்யெண்ணைக் கழிப்பதற்குப் பதிலாக அந்த மெய்யெண்ணின் கூட்டல் நேர்மாறு கூட்டப்படுகிறது.

3 − π = 3 + (−π).

இவ்வாறு வரையறுப்பதால், மெய்யெண்களின் வளையத்தில், கழித்தலை ஒரு புதிய செயலியாக அறிமுகப்படுத்த வேண்டிய அவசியிமில்லாமல் எளிமையாகிறது. பொதுவாக ஒரு வளையம் இரண்டு செயலிகளைக் கொண்டிருக்கும். முழுவெண் வளையத்தில் அவ்விரு செயலிகளும் கூட்டலும் பெருக்கலுமாகும். வளையத்தில் ஏற்கனவே கூட்டல் நேர்மாறு என்ற கருத்து உள்ளது; ஆனால் கழித்தல் என்ற தனிச் செயலி இல்லை. எனவே குறியிடப்பட்ட எண்களின் கூட்டலாகக் கழித்தலைக் கொள்வதால், வளையத்தின் எடுகோள்களை கழித்தலுக்கும் பயன்படுத்த முடிகிறது

கழித்தல் எதிர்பரிமாற்றுப் பண்பு கொண்டது. அதாவது கழித்தலில் உறுப்புகளின் வரிசை மாற்றப்பட்டால் கிடைக்கும் விடை, மூல விடையின் எதிர்ம எண்ணாக இருக்கும்.

a , b இரு எண்கள் எனில்,

a − b = −(b − a).

கழித்தலுக்கு சேர்ப்புப் பண்பு இல்லை

"a − b − c" என்ற கழித்தலை (a − b) − c மற்றும் a − (b − c) என எடுத்துக்கொண்டால் இரண்டும் வெவ்வேறு விடைகளைத் தரும். எனவே இச்சிக்கலைத் தவிர்க்க, செயலியை அமல்படுத்தும் வரிசை முறை தெளிவாகத் தரப்பட்டிருக்க வேண்டும்.

முழுவெண்களில், எந்தவொரு முழுவெண்ணிலுமிருந்தும் (a) எண் 1 ஐக் கழித்தால் கிடைக்கும் எண்ணானது, (a − 1), மூல எண்ணைவிடச் சிறிய முழுவெண்களிலேயே மிகப்பெரிய முழுவெண்ணாகும். மேலும் (a − 1) என்பது a இன் முன்னி (predecessor) எனப்படும்.

கிலோகிராம், மீட்டர், அங்குலம் போன்ற அலகுகளோடு கூடிய இரு அளவை எண்களைக் கழிக்கும் போது, அவை இரண்டும் ஒரே அலகுகளில் அமைந்திருத்தல் அவசியம். கழித்து வரும் விடையும் பெரும்பாலும் அதே அலகிலேயே அமைந்திருக்கும்.

100 கி.மீ. - 28 கி.மீ. = 72 கி.மீ.

54 அடி - 43 அடி = 11 அடி

விழுக்காடுகளின் மாற்றமானது, விழுக்காடு வித்தியாசம் மற்றும் சதவீத முனைப்புள்ளி வித்தியாசம் என இருவகையாக உள்ளது. விழுக்காடு வித்தியாசம் என்பது இரு கணியங்களின் சார்மாற்றத்தின் விழுக்காடாகும். சதவீத முனைப்புள்ளி வித்தியாசம் என்பது இரு விழுக்காடுகளின் வித்தியாசம் ஆகும்.^[5][6][7]

எடுத்துக்காட்டு: ஒரு தொழிற்சாலையில் உற்பத்தி செய்யப்பட்ட பொருட்களில் 30% குறைபாடுள்ளவை; ஆறுமாதங்களுக்குப் பின்னர் 20% பொருட்கள் குறைபாடுள்ளவை என்க.

• சதவீத முனைப்புள்ளி வித்தியாசம் = 20% -30% = -10% = -10 சதவீதப்புள்ளிகள்
• விழுக்காடு வித்தியாசம் = (-10/30) x 100 = −33 1/3%

கழித்தல் செயலானது பல்வேறு முறைகளில் செய்யப்படுகிறது.

எடுத்துக்காட்டு:

• 
  1 + ... = 3
• 
  கோட்டுக்கீழ் வித்தியாசம் எழுதப்படுகிறது.
• 
  9 + ... = 5
  தேவைப்படும் கூட்டுத்தொகை (5) மிகச்சிறியது!
• 
  எனவே அதனுடன் 10 கூட்டப்பட்டு, கழிபடுவெண்ணின் அடுத்த உயர் இலக்கத்தின் கீழ் 1 எழுதப்படுகிறது.
• 
  9 + ... = 15
  இப்பொழுது முன்போல வித்தியாசம் காணலாம்.
• 
  (4 + 1) + ... = 7
• 
  வித்தியசம் கோட்டுக்குக் கீழ் எழுதப்படுகிறது.
• 
  இறுதி வித்தியாசம்.

எடுத்துக்காட்டு:

• 
  7 − 4 = 3
  இவ்விடை பென்சிலால் குறிக்கப்படுகிறது.
• 
  கழிமுக எண்ணின் அடுத்த இலக்கம் கழிபடு எண்ணின் இலக்கத்தைவிடச் சிறியதாக உள்ளதால், பென்சிலால் எழுதப்பட்ட எண்ணிலிருந்து 1 கழிக்கப்பட்டு மனக்கணக்காக கழிமுதலெண் இலக்கத்தோடு 10 கூட்டப்படுகிறது.
• 
  15 − 9 = 6
• 
  கழிமுதலெண்ணின் அடுத்த இலக்கம் கழிபடுஎண் இலக்கத்தைவிடப் பெரியதாக உள்ளதால் அப்படியே வைத்துக்கொண்டு வித்தியாசம் காணப்படுகிறது.
• 
  3 − 1 = 2

இம்முறையில் கழித்தல் வலமிருந்து இடமாகச் செய்யப்படுகிறது.

கழிமுதல் எண்ணின் வலக்கோடி இலக்கம் கழிபடு எண்ணின் வலக்கோடி இலக்கத்தை விடச் சிறியதாக இருந்தால் அதனுடன் 10 கூட்டப்பட்டு பின்னர் வித்தியாசம் காணப்படுகிறது. கூட்டப்ப்பட்ட இந்த 10 ஆனது, இடப்பக்க முந்தைய இலக்கத்திலிருந்து கடன்பெற்றதாகக் கொள்ளப்பட்டு, அந்த இலக்கத்திலிருந்து 1 குறைத்துக்கொள்ளப்படும். இவ்வாறு அடுத்தடுத்த இடப்பக்க இலக்கங்கள் தேவைப்பட்டால் கடன் வாங்கும் முறையில் கழிக்கப்படுகின்றன.

எடுத்துக்காட்டு:

• 
  3 − 1 = ...
• 
  கோட்டின்கீழ் வித்தியாசம் எழுதப்படுகிறது.
• 
  5 − 9 = ...
  அடுத்த கழிமுதல் எண் (5) சிறியதாக உள்ளது!
• 
  அதனுடன் 10 கூட்டப்படுகிறது. இந்த 10 ஆனது 5 க்கு இடப்பக்க கழிமுதல் இலக்கமான 7 இலிருந்து 1 கடனாகப்பெறப்பட்டு 7, 6 ஆகக் குறைக்கப்படுகிறது.
• 
  15 − 9 = ...
  வித்தியாசம் கண்டுபிடிக்கப்பட்டு கோட்டுக்குக் கீழே எழுதப்படுகிறது.
• 
  6 − 4 = ...
• 
  வித்தியாசம் கோட்டுக்குக் கீழே எழுதப்படுகிறது.
• 
  இறுதி வித்தியாசம்.

அமெரிக்க முறையிலிருந்து இம்முறை சிறிது மாற்றம் கொண்டது. தேவைப்படும் கழிமுதல் இலக்கங்கள் அனைத்துக்கும் கடன்வாங்கி வைத்துக்கொண்ட பின்னரே, கழித்தல் தொடங்கப்படுகிறது.^[8]

Example:

• 
  1 − 3 = கழிக்க முடியாது.
  இடப்பக்க 5 லிருந்து 1 கடன்பெறப்பட்டு, 10 ஆக 1 உடன் கூட்டப்படுகிறது. இடப்புற 5, 4 ஆகக் குறைகிறது.
• 
  4 − 9 = கழிக்க முடியாது.
  இடப்பக்க 7 லிருந்து 1 கடன்பெறப்பட்டு, 10 ஆக 4 உடன் கூட்டப்படுகிறது. இடப்புற 7, 6 ஆகக் குறைகிறது.
• 
  வலமிருந்து இடமாக கழித்தல் செய்யப்படுகிறது:
  11 − 3 = 8
• 
  14 − 9 = 5
• 
  6 − 4 = 2

செங்குத்துக் கழித்தல் முறைகளிலிருந்து பகுதி வித்தியாச முறை மாறுப்பட்டதாகும். இதில் கடன்பெறுதல் இல்லை. அதற்குப் பதிலாக, கழிமுதலெண், கழிபடுவெண் இவையிரண்டில் பெரிய எண்ணிலிருந்து சிறிய எண் கழிக்கப்பட்டு இடமதிப்புடன் வித்தியாசம் கோட்டின் கீழ் கூட்டல்/கழித்தல் குறியுடன் எழுதிக்கொள்ளப்படுகிறது. பகுதி வித்தியாசங்களின் கூட்டுத்தொகையே தேவையான இறுதி வித்தியாசமாக இருக்கும்.^[9]

எடுத்துக்காட்டு:

• 
  700 − 400 = 300
  கழிமுதல் எண், கழிபடு எண்ணைவிடப் பெரியது என்பதால் பகுதி வித்தியாசம் +700.
• 
  90 − 50 = 40
  கழிபடு எண், கழிமுதல் எண்ணைவிடப் பெரியது என்பதால் பகுதி வித்தியாசம் -40.
• 
  3 − 1 = 2
  கழிமுதல் எண், கழிபடு எண்ணைவிடப் பெரியது என்பதால் பகுதி வித்தியாசம் +2
• 
  +300 − 40 + 2 = 262

இலக்கம் இலக்கமாக வித்தியாசம் காண்பதற்குப் பதிலாக, கழிபடு எண்ணிக்கும் கழிமுதல் எண்ணிக்கும் இடையே உள்ள எண்களின் எண்ணிக்கையைக் கீழிருந்து மேல்நோக்கி எண்ணிக் கண்டுபிடிக்கும் முறையாகும்.^[10]

எடுத்துக்காட்டு: 1234 − 567 = ? :

• 567 + 3 = 570
• 570 + 30 = 600
• 600 + 400 = 1000
• 1000 + 234 = 1234
• 3 + 30 + 400 + 234 = 667 = இறுதி வித்தியாசம்.

மனக்கணக்காகக் கழித்தலைச் செய்வதற்கு இந்தச் சிறுசிறு படிகளாகப் பிரித்துக் கழித்தல் முறை உதவியாக இருக்கும்.^[11]

எடுத்துக்காட்டு: 1234 − 567 = ? :

• 1234 − 500 = 734
• 734 − 60 = 674
• 674 − 7 = 667

கழிமுதல் எண் மற்றும் கழிபடு எண் இரண்டுடனும் ஒரேயெண்ணைக் கூட்ட/கழிக்க இறுதிவிடையில் மாற்றம் இருக்காது என்ற கருத்தின் அடிப்படையில் இம்முறை செயற்படுத்தப்படுகிறது. கழிபடுஎண்ணின் இலக்கத்தில் பூச்சியம் வருவதற்குத் தேவையான எண் கூட்டப்படுகிறது.^[12]

எடுத்துக்காட்டு:

"1234 − 567 = ?" :

• 1234 − 567 = 1237 − 570 = 1267 − 600 = 667

• Brownell, W. A. (1939). Learning as reorganization: An experimental study in third-grade arithmetic, Duke University Press.
• Subtraction in the United States: An Historical Perspective, Susan Ross, Mary Pratt-Cotter, The Mathematics Educator, Vol. 8, No. 1 (original publication) and Vol. 10, No. 1 (reprint.) பரணிடப்பட்டது 2017-08-11 at the வந்தவழி இயந்திரம் பி.டி.எவ்

விக்கிமீடியா பொதுவகத்தில்,
கழித்தல் (கணிதம்)
என்பதில் ஊடகங்கள் உள்ளன.

• Hazewinkel, Michiel, ed. (2001), "Subtraction", Encyclopedia of Mathematics, Springer, ISBN 978-1556080104
• Printable Worksheets: Subtraction Worksheets பரணிடப்பட்டது 2012-11-19 at the வந்தவழி இயந்திரம், One Digit Subtraction, Two Digit Subtraction, Four Digit Subtraction, and More Subtraction Worksheets
• Subtraction Game at cut-the-knot
• Subtraction on a Japanese abacus selected from Abacus: Mystery of the Bead

• கூட்டல்
• பெருக்கல்
• வகுத்தல்