Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«еЯ»ЇЯ«цЯ«┐Я«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐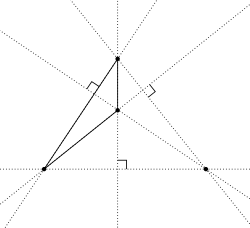 Я«хЯ«ЪЯ«┐Я«хЯ«хЯ«┐Я«»Я«▓Я«┐Я«▓Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«еЯ»ЇЯ«цЯ«┐Я«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«џЯ»ЇЯ«џЯ«еЯ»ЇЯ«цЯ«┐Я«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐ (orthocentric system) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»ЂЯ«цЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▓Я««Я»ѕЯ«еЯ»ЇЯ«ц Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«ЋЯ«БЯ««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«јЯ«хЯ»ѕЯ«»Я»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«еЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«Ћ Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ«ЙЯ«хЯ«цЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«ЁЯ««Я»ѕЯ«»Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Є Я«ЄЯ«цЯ»ЇЯ«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»Ї Я«њЯ«░Я»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«еЯ»ЇЯ«цЯ«┐Я«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ, Я«ЁЯ«хЯ»ѕ Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ«┐Я«▒ Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«еЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Є Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«њЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ-Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ»ЂЯ«▒Я»ЇЯ«▒Я»ЂЯ«хЯ«ЪЯ»ЇЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«єЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«џЯ«« Я«ЁЯ«│Я«хЯ«ЙЯ«ЕЯ«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«фЯ»іЯ«цЯ»Ђ Я«њЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ-Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«еЯ»ЇЯ«цЯ«┐Я«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ«┐Я«» Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«ЕЯ«цЯ«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«њЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ-Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ѕЯ«»Я««Я«ЙЯ«ЕЯ«цЯ»Ђ, Я«ЁЯ«еЯ»ЇЯ«ц Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ«┐Я«БЯ«┐Я«хЯ»Ђ Я««Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї. Я«ЁЯ«еЯ»ЇЯ«ц Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЈЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЄЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕ Я«ЄЯ«БЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ«┐Я«» Я«єЯ«▒Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«еЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»Ї Я«хЯ«┤Я«┐Я«»Я«ЙЯ«Ћ Я«ЄЯ«еЯ»ЇЯ«цЯ«фЯ»Ї Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї Я«њЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ-Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЁЯ«еЯ»ЇЯ«ц Я«єЯ«▒Я»Ђ Я«еЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«јЯ«еЯ»ЇЯ«цЯ«хЯ»іЯ«ЕЯ»ЇЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ»ѓЯ«░Я««Я»Є Я«њЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ-Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«єЯ«░Я««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«┐Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ»ЂЯ«▒Я»ЇЯ«▒Я»ЂЯ«хЯ«ЪЯ»ЇЯ«Ъ Я««Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЁЯ««Я»ЇЯ««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«еЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ«┐Я«» Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ«ЙЯ«хЯ«цЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«еЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЄЯ«еЯ»ЇЯ«цЯ«фЯ»Ї Я«фЯ»іЯ«цЯ»Ђ Я«њЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ-Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї. Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«јЯ«хЯ»ѕЯ«»Я»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«┐Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ«┐Я«» Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЅЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї, Я«хЯ»єЯ«│Я«┐Я«хЯ«ЪЯ»ЇЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ«┐Я«» 16 Я«хЯ«ЪЯ»ЇЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЄЯ«еЯ»ЇЯ«цЯ«фЯ»Ї Я«фЯ»іЯ«цЯ»Ђ Я«њЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ-Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«цЯ»іЯ«ЪЯ»ЂЯ««Я»Ї.[1] Я«фЯ»іЯ«цЯ»Ђ Я«єЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐Я«ЋЯ»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»ЇЯ«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«еЯ»ЇЯ«цЯ«┐Я«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«┐Я«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ«Ћ Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«єЯ«▒Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«ЙЯ«Ћ Я«еЯ»ђЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ, Я«ЁЯ«хЯ»ѕ Я«ЈЯ«┤Я»Ђ Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕЯ«цЯ»Ї Я«цЯ»ІЯ«▒Я»ЇЯ«▒Я»ЂЯ«хЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я«ЈЯ«┤Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«еЯ»ЇЯ«цЯ«┐Я«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї, Я««Я»ђЯ«цЯ««Я»ЂЯ«│Я»ЇЯ«│ Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕ Я«ЄЯ«БЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я«ЙЯ«ЕЯ«цЯ»Ђ, Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«еЯ»ЇЯ«цЯ«┐Я«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ«┐Я«» Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Е Я«єЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐Я«ЋЯ»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«еЯ»ЇЯ«цЯ«┐Я«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЄЯ«еЯ»ЇЯ«цЯ«фЯ»Ї Я«фЯ»іЯ«цЯ»Ђ Я«єЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐Я«ЋЯ»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»ѕЯ«»Я««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї, Я««Я»ђЯ«цЯ««Я»ЂЯ«│Я»ЇЯ«│ Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ЂЯ««Я»Ї Я«єЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐Я«ЋЯ»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«хЯ»єЯ«│Я«┐Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»ѕЯ«»Я«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЁЯ««Я»ѕЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я««Я»ѓЯ«▓Я«цЯ»ЇЯ«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«фЯ»іЯ«цЯ»Ђ Я«њЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ-Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЁЯ«░Я»ЂЯ«ЋЯ«ЙЯ««Я»ѕЯ«»Я«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»Є Я«фЯ»іЯ«цЯ»Ђ Я«єЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐Я«ЋЯ»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»ѕЯ«»Я««Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»ЇЯ«фЯ«ЪЯ«┐, Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»ѕЯ«»Я««Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«хЯ»єЯ«│Я«┐Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»ѕЯ«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«еЯ»ЇЯ«цЯ«┐Я«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»єЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ Я«ЁЯ«▒Я«┐Я«»Я«▓Я«ЙЯ««Я»Ї.[2]:p.182 Я«ЄЯ«»Я«▓Я»ЂЯ«▒Я»Ђ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«еЯ»ЇЯ«цЯ«┐ Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї, Я«єЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐Я«ЋЯ»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»ѕЯ«»Я««Я«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ѕ H Я«јЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ђЯ«цЯ««Я»ЂЯ«│Я»ЇЯ«│ Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕ A, B, C Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«цЯ»ЇЯ«цЯ«▓Я»Ї Я«хЯ«┤Я««Я»ѕЯ«»Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«ЄЯ«еЯ«ц Я«ЄЯ«»Я«▓Я»ЂЯ«▒Я»Ђ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї (normalized configuration) H Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«ЙЯ«ЕЯ«цЯ»Ђ Я«јЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї ABC Я«ЄЯ«ЕЯ»Ї Я«ЅЯ«ЪЯ»ЇЯ«фЯ»ЂЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»ЂЯ««Я»Ї. Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї ABC Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ«┐Я«» Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї ABC , ABH , ACH , BCH Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«┐Я«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ«Ћ Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«єЯ«▒Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї: AB, AC, BC, AH, BH, CH. Я«ЄЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«ЙЯ«▓Я»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЈЯ«┤Я»Ђ Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»Ї: A, B, C, H (Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«џЯ»ЇЯ«џЯ«еЯ»ЇЯ«цЯ«┐Я«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»Ї); HA, HB, HC (Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї ABC Я«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«єЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐Я«ЋЯ»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ«│Я»Ї). Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ«│Я»ЇЯ«њЯ«░Я»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«еЯ»ЇЯ«цЯ«┐Я«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«ЙЯ«▓Я»Ї Я«ЁЯ««Я»ѕЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ«┐Я«» Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«ЕЯ»ЇЯ«▒Я«┐Я«▓Я»ЂЯ««Я»Ї Я«єЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐Я«ЋЯ»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я»ѓЯ«▓ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«џЯ»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«┤Я«┐Я«»Я«ЙЯ«ЋЯ«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«ЪЯ»Ђ Я«єЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐Я«ЋЯ»Ї Я«ЁЯ«џЯ»ЇЯ«џЯ»Ђ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЁЯ«џЯ»ЇЯ«џЯ»Ђ Я«јЯ«Е Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«јЯ«ЕЯ«хЯ»Є Я«њЯ«░Я»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«еЯ»ЇЯ«цЯ«┐Я«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«єЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐Я«ЋЯ»Ї Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«Е. Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«еЯ»ЇЯ«цЯ«┐Я«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«ЄЯ«»Я«▓Я»ЂЯ«▒Я»Ђ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї, Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї ABC Я«ЄЯ«ЕЯ»Ї Я«єЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐Я«ЋЯ»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї HAHBHC Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«┐Я«▓Я»Ї Я«єЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐Я«ЋЯ»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї HB HC, HA HB, HA HC Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ѓЯ«▓Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї ABC Я«ЄЯ«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї BC , AB , AC Я«љ Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є OA, OC, OB Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЄЯ««Я»ЇЯ««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«┤Я«┐Я«»Я»Є Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ Я«єЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐Я«ЋЯ»Ї Я«ЁЯ«џЯ»ЇЯ«џЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї[3]. Я«ЄЯ«цЯ»Є Я«фЯ»ІЯ«▓ Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я««Я«▒Я»ЇЯ«▒ Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї (ABH, ACH and BCH) Я«єЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐Я«ЋЯ»Ї Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї. Я«хЯ»ЄЯ«▒Я»ЂЯ«џЯ«┐Я«▓ Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї
Я«ЄЯ«цЯ«┐Я«▓Я»Ї R -Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЁЯ«│Я«хЯ»ЂЯ«џЯ»Ї Я«џЯ»ЂЯ«▒Я»ЇЯ«▒Я»ЂЯ«хЯ«ЪЯ»ЇЯ«Ъ Я«єЯ«░Я««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«џЯ»ѕЯ«ЕЯ»Ї Я«хЯ«┐Я«цЯ«┐Я«»Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»Ђ:
Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ»ІЯ«│Я»ЇЯ«ЋЯ«│Я»Ї
Я«хЯ»єЯ«│Я«┐Я«»Я«┐Я«БЯ»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї
|
Portal di Ensiklopedia Dunia















