செங்கோணம்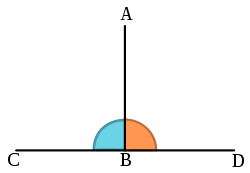

வடிவவியலில் செங்கோணம் (right angle) என்பது ஒரே நேர்கோட்டின் இரண்டு அரைப்பகுதிகளால் உண்டாகும் கோணத்தை இருசமக்கூறிடும் கோணமாகும். ஒரு நேர்கோட்டின் மீது முனைப்புள்ளி அமையுமாறு ஒரு கதிர் வரையப்படுகிறது என்க. அக்கதிர், மற்றும் அந்த கோடு இவற்றுக்கிடையே உண்டாகும் இரு அடுத்துள்ள கோணங்கள் சமமாக இருந்தால் அவ்விரண்டு கோணங்களும் செங்கோணங்களாக இருக்கும்.^[1] சுழற்சியின் வாயிலாகக் கூறுவதென்றால் செங்கோணம் ஒரு முழு சுழற்சியில் கால் பகுதியாகும்.^[2]

செங்கோணத்துடன் தொடர்புடைய முக்கிய வடிவவியல் கருத்துருக்கள் செங்குத்துக் கோடுகளும் செங்குத்துத் தன்மையுமாகும். செங்குத்துக் கோடுகள் ஒன்றையொன்று வெட்டிக்கொள்ளும் புள்ளியில் உண்டாகும் கோணங்கள் செங்கோணங்களாக இருக்கும். ஒரு முக்கோணத்தின் ஒரு கோணம் செங்கோணமாக இருந்தால் அம்முக்கோணம் செங்கோண முக்கோணம் என அழைக்கப்படுகிறது.^[3] முக்கோணவியலுக்கு அடிப்படையாக அமைவது செங்கோண முக்கோணங்களாகும்.^[3]

செங்கோணத்தைக் குறிக்கும் ஆங்கிலச் சொல் right angle என்பது angulus rectus என்ற இலத்தீன் மொழிச் சொல்லின் நேரான மொழிபெயர்ப்பாகும்; இதிலுள்ள rectus - செங்குத்தான என்பதைக் குறிக்கும்.

படங்களில் வழக்கமாக செங்கோணத்தைக் குறிப்பதற்கு அச்செங்கோணத்துடன் சேர்த்து ஒரு சிறு சதுரம் ஏற்படும்படி மற்றொரு சிறு செங்கோணம் வரையப்படுகிறது. மாறாக சில சமயங்களில் செங்கோணம் வளைவு கோணத்துக்குள் ஒரு சிறு புள்ளியுடன் குறிக்கப்படுகிறது.

செங்கோணங்கள், யூக்ளிடின் எலிமெண்ட்சில் அடிப்படைக் கருத்தாக உள்ளன. புத்தகம் 1, வரையறை 10 செங்குத்துக் கோடுகளை வரையறுக்கிறது. யூக்ளிட், வரையறை 11 மற்றும் 12-ல் செங்கோணத்தைப் பயன்படுத்தி, குறுங்கோணங்களை வரையறுக்கும்போது செங்கோணத்தை விட அளவில் சிறிய கோணங்கள் குறுங்கோணங்கள் என்றும் செங்கோணத்தைவிட அளவில் பெரியவை விரிகோணங்கள் என்றும் வரையறுத்துள்ளார்.^[4] இரு கோணங்களின் கூடுதல் செங்கோணம் என்றால் அவை நிரப்புக் கோணங்கள் எனப்படும்.^[5]

புத்தகம் 1 எடுகோள் 4 -ன்படி, அனைத்து செங்கோணங்களும் சமம். செங்கோணத்தை அலகாகப் பயன்படுத்தி மற்ற கோணங்களை அளப்பதற்கு யூக்ளிட் இதைப் பயன்படுத்தினார்.^[6]

செங்கோணத்தைப் பின்வரும் அலகுகளில் எழுதலாம்:

• ¹/₄ திருப்பம்.
• 90° (பாகை)
• ^π/₂ ரேடியன்
• 100 கிரேட்
• 8 புள்ளிகள் (of a 32-புள்ளிகளுடைய திசை அளவிட்ட வட்டத்தில்)
• 6 மணி (வானவியல் மணிக்கோணம் (hour angle))

பழங்காலத்திலிருந்தே மரம் மற்றும் கட்டிடத் தொழிலாளர்கள் ஒரு கோணம் உண்மையிலேயே செங்கோணமாக உள்ளதா என்பதைக் கண்டறிய ஒரு எளிய முறையைக் கண்டறிந்திருந்தனர். அந்த முறை, புகழ்பெற்ற பித்தோகரசின் மும்மை (3, 4, 5) -ஐச் சார்ந்திருந்தமையால் 3-4-5 வழிமுறை எனப்பட்டது. சரிபார்க்கப்பட வேண்டிய கோணத்தின் ஒரு பக்கத்தில் 3 அலகு நீளமுள்ள நேர்கோட்டுத்துண்டும் மறுபக்கத்தில் 4 அலகு நீளமுள்ள நேர்கோட்டுத்துண்டும் எடுத்துக்கொண்டு இவற்றின் மறுமுனைகளை இணைக்கும் கோட்டுத்துண்டின் நீளம் காண வேண்டும். எடுத்துக்கொண்ட கோணம் செங்கோணமாக இருந்தால், பித்தாகரசு தேற்றப்படி, இக்கோட்டுத்துண்டின் நீளம் சரியாக 5 அலகாக இருக்கும். இம்முறையில் சரிபார்ப்பது எளிது. தொழில்நுட்பக் கருவிகள் எதுவும் இல்லாமலே அளந்து விடமுடியும்.

தேலேசுத் தேற்றத்தின்படி ஒரு அரைவட்டத்துள் அமையும் கோணம் செங்கோணமாகும்.

• Wentworth, G.A. (1895). A Text-Book of Geometry. Ginn & Co.
• Euclid, commentary and trans. by T. L. Heath Elements Vol. 1 (1908 Cambridge) Google Books