நிகழ்ச்சி (நிகழ்தகவு)

இந்தக் கட்டுரையில் மேற்கோள்கள் அல்லது உசாத்துணைகள் எதுவும் இல்லை. நடுநிலையான மேற்கோள்கள் அல்லது உசாத்துணைகளைக் கொடுத்து இந்தக் கட்டுரையை மேம்படுத்த நீங்களும் உதவலாம். உசாத்துணைகள் இல்லாத கட்டுரைகள் விக்கிப்பீடியாவிலிருந்து நீக்கப்படலாம்.

நிகழ்தகவுக் கோட்பாட்டில் ஒரு சமவாய்ப்புச் சோதனையின் கூறுவெளியிலுள்ள ஒவ்வொரு உட்கணமும் நிகழ்ச்சி (Event) எனப்படும். கூறுவெளியின் அடுக்குக் கணத்தின் ஒவ்வொரு உறுப்பும் ஒரு நிகழ்ச்சியாகும். கூறுவெளி முடிவுறுகணமாக இருந்தால் மட்டுமே நிகழ்ச்சியை இவ்வாறு வரையறுக்கலாம்.

உட்கணங்களின் வரையறைப்படி ஒவ்வொரு கணத்திற்கும் அந்தக்கணமே ஓர் உட்கணமாகவும், வெற்றுக்கணம் ஓர் உட்கணமாகவும் அமையும் என்பதால் கூறுவெளியின் உட்கணங்களாக அதே கூறுவெளி கணமும் வெற்றுக்கணமும் அமைகின்றன. எனவே கூறுவெளி மற்றும் வெற்றுக்கணம் இரண்டும் இரு நிகழ்ச்சிகளைக் குறிக்கும்.

• நடக்கக்கூடிய அனைத்து நிகழ்வுகளின் கணமான கூறுவெளி, உறுதியாக அல்லது நிச்சயமாக நடக்கக்கூடிய நிகழ்ச்சி (Sure event) எனப்படுகிறது. இதன் நிகழ்தகவு 1.
• வெற்றுக்கணம் நடக்க இயலா நிகழ்ச்சி (Impossible event) என்று அழைக்கப்படுகிறது. இதன் நிகழ்தகவு 0.

ஒரு நிகழ்ச்சியென்பது கூறுவெளியின் உட்கணமாக அமையும் என்பதால் அது ஓருறுப்புக்கணமாகவோ, வெற்றுக்கணம் அல்லது அனைத்து உறுப்புகளையும் கொண்ட கணமாகவோ அல்லது பல உறுப்புகளைக் கொண்ட தக்க உட்கணமாகவோ இருக்கலாம்.

ஒரு பகடையை வீசும்போது கூறுவெளி: ${\displaystyle \{{\text{1,2,3,4,5,6}}\}}$. இதில்,

• ஆறுக்கு மேற்பட்ட எண் கிடைக்ககூடிய நிகழ்ச்சி:

${\displaystyle \{{\text{ }}\}}$

• எண் 4 கிடைக்கக்கூடிய நிகழ்ச்சி:

${\displaystyle \{{\text{4}}\}}$

• 3க்கு கீழ் உள்ள எண்கள் கிடைக்கக்கூடிய நிகழ்ச்சி:

${\displaystyle \{{\text{1,2}}\}}$

• ஒற்றை எண்கள் கிடைக்கக்கூடிய நிகழ்ச்சி

${\displaystyle \{{\text{1,3,5}}\}}$

• 2க்கு மேற்பட்ட எண்கள் கிடைக்கக்கூடிய நிகழ்ச்சி:

${\displaystyle \{{\text{3,4,5,6}}\}}$

• 1க்கு மேற்பட்ட எண்கள் கிடைக்கக்கூடிய நிகழ்ச்சி:

${\displaystyle \{{\text{2,3,4,5,6}}\}}$

• ஏதேனும் ஒரு எண் கிடைக்கக்கூடிய நிகழ்ச்சி

${\displaystyle \{{\text{1,2,3,4,5,6}}\}}$

சாதாரண நிகழ்ச்சி அல்லது அடிப்படை நிகழ்ச்சி (simple event) என்பது ஒரு சமவாய்ப்பு சோதனையில் கிடைக்கக்கூடிய நிகழ்வுகளில் (முடிவுகள்) அதற்கு மேலும் சிறு சிறு நிகழ்வுகளாகப் பிரிக்க இயலாதவை ஆகும்.

எடுத்துக்காட்டு:

ஒரு பகடையை வீசும் சோதனையின் அடிப்படை நிகழ்ச்சிகள்:

${\displaystyle \{{\text{1}}\},}$ ${\displaystyle \{{\text{2}}\},}$ ${\displaystyle \{{\text{3}}\},}$ ${\displaystyle \{{\text{4}}\},}$ ${\displaystyle \{{\text{5}}\},}$ ${\displaystyle \{{\text{6}}\}.}$

இவற்றை இதற்கு மேல் சிறு சிறு நிகழ்ச்சிகளாகப் பிரிக்க முடியாது.

ஒன்றையொன்று விலக்கும் நிகழ்ச்சிகள் (mutually exclusive events) என்பவை ஒரு சமவாய்ப்புச் சோதனையில் தமக்குள் பொதுவான அடிப்படை நிகழ்ச்சிகள் இல்லாத இரண்டு அல்லது இரண்டுக்கு மேற்பட்ட நிகழ்ச்சிகள் ஆகும்.

அதாவது ஒரு சோதனையில், ஒரு நிகழ்ச்சி நிகழ்வதால் மற்றொரு நிகழ்ச்சி நிகழமுடியாது எனில் அவை இரண்டும் ஒன்றையொன்று விலக்கும் நிகழ்ச்சிகள் எனப்படும்.

எடுத்துக்காட்டு:

ஒருபகடையை வீசும் சோதனையில் இரட்டையெண்கள் விழக்கூடிய நிகழ்ச்சியான ${\displaystyle \{{\text{2,4,6}}\},}$ ஒற்றையெண்கள் விழக்கூடிய நிகழ்ச்சியான ${\displaystyle \{{\text{1,3,5}}\}}$ இரண்டும் ஒன்றையொன்று விலக்கும் நிகழ்ச்சிகள். ஒன்று நிகழும்போது மற்றொன்று நிகழாது.

ஒரு சமவாய்ப்புச் சோதனையில் ${\displaystyle A,}$ ${\displaystyle B}$ இரண்டும் ஒன்றையொன்று விலக்கும் நிகழ்ச்சிகள் எனில் கணக் குறியீட்டில் அதனைப் பின்வருமாறு குறிக்கலாம்:

${\displaystyle A\cap B=\varnothing }$.

இங்கு ${\displaystyle \varnothing }$ என்பது வெற்றுக் கணம்

கூறுவெளி S ல் உள்ள விளைவுகள் அனைத்தும் சமவாய்ப்புள்ளதாக இருந்தால் அதிலுள்ள ஒரு நிகழ்ச்சி A இன் நிகழ்தகவு காணும் வாய்ப்பாடு:

${\displaystyle \mathrm {P} (A)={\frac {n(A)}{n(S)}}\,}$

n(A) என்பது நிகழ்ச்சி A ன் கணத்தில் உள்ள உறுப்புகளின் எண்ணிக்கையையும் n(S) என்பது கூறுவெளி Sல் உள்ள உறுப்புகளையும் குறிக்கிறது. மேலே தரப்பட்டுள்ள எடுத்துக்காட்டிலுள்ள நிகழ்ச்சிகளின் நிகழ்தகவுகளை இந்த வாய்ப்பாட்டைப் பயன்படுத்திக் காணலாம்.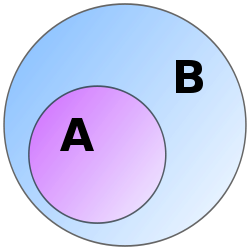

நிகழ்ச்சிகள் அனைத்தும் கணங்களாக வரையறுக்கப்படுவதால் நிகழ்ச்சிகளை வென்படங்கள் மூலமாகவும் விளக்கலாம். வலப்புறம் இணைக்கப்பட்டுள்ள படத்தில்:

B என்பது கூறுவெளி,

A என்பது நிகழ்ச்சி.

அவற்றின் பரப்பளவு விகிதப்படி Aன் நிகழ்தகவு தோராயமாக 0.4.