பண்டைய கிரேக்க வானியல் கிரேக்க வானியல் (Greek astronomy) என்பது கிரேக்கமொழியில் பண்டைய செவ்வியல் காலத்தில் எழுதப்பட்டவானியலாகும். இதில் பண்டைய கிரெக்கம், எலனியக் கால கிரேக்க நாகரிகம், கிரேக்க-உரோம அரசுக் காலம், பிற்பண்டைக்காலம் ஆகிய வரலாற்றுக்கட்டங்கள் அடங்கும். இது புவிப்பரப்பில் கிரேக்கத்தை மட்டும் உள்ளடக்காது. மேலும் இது கிரேக்கர்களால் மட்டும் எழுதப்பட்டதல்ல. ஏனெனில் கிரேக்க மொழி இக்கால கட்டங்களில் புலமைப்பரப்பு மொழியாக அலெக்சாந்தரின் உலக வெற்றிக்குப் பிறகு எலனிய ஆட்சிப் பரப்பு முழுவதிலும் ஓங்கியிருந்தது. இக்கட்டம் எலனிய வானியல் எனவும் வழங்கப்படும். முந்து வரலாற்றுக்கட்டம் பண்டைய கிரேக்கச் செவ்வியல் வானியல் எனப்படுகிறது. எலனிய, உரோமானிய ஆட்சிக் காலங்களில் கிரெக்கர்களும் கிரேக்கஞ்சாராத வானியலாளர்களும் ஒன்றிணைந்து கிரேக்க மரபு சார்ந்து தாலமிய காலத்தில் மியூசியத்திலும் அலெக்சாந்திரியா நூலகத்திலும் வானியலை வளர்த்தனர். கிரேக்க, எலனிய வானியலாளர்களால் வென்றெடுக்கப்பட்ட வானியலின் வளர்ச்சி வானியல் வரலாற்றில் மிக சீரிய கட்டமாகக் கருதப்படுகிறது. கிரேக்க அறிவியல் தொடக்க முதலே வானியல் நிகழ்வுகளுக்கான பகுத்தறிவு சார்ந்த புறநிலை விளக்கத்தை அடிப்படையாக்க் கொண்டிருந்தது.[1] பெரும்பாலான வட அரைக்கோள விண்மீன்குழுக்களும் விண்மீன்கள்,கோள்கள், சிறுகோள்கள் ஆகியவற்றின் பெயர்கள் கிரேக்க வானியலில் இருந்து பெறப்பட்டவையே,[2] கிரேக்க வானியல் எகிப்திய ,பாபிலோனிய வானியலின் தாக்கம் உற்றத்தாகும்; மாறாக கிரேக்க வானியல் இந்திய, அராபிய, மேலைய வானியல் வளர்ச்சிக்கு உந்துதல் அளித்ததாகக் கருதப்படுகிறது. தொல்கிரேக்க வானியல்இனங்கானமுடிந்த விண்மீன்களையும் விண்மீன் குழுக்களையும் விண்மீன் கொத்துகளையும் தன் எசியோது நூலில் ஃஓமர் குறிப்பிடுகிறார். மேலும் தன் இலியாதிலும் ஒடிசியிலும், ஃஓமர் பின்வரும் வான்பொருள்களைக் குறிப்பிடுகிறார்:
 கி.மு 7 ஆம் நூற்றாண்டு எழுத்தளரான எசியோது இப்பட்டிய்லில் ஆர்க்தூரசு எனும் விண்மீனை தனது பணிகளும் நாட்களும் என்ற கவிதைக் கால அட்டவணையில் aசேர்த்துள்ளார். ஃஓமரோ ஃஎசியோதோ அறிவியல் எழுத்தாளர்கள் அல்லவென்றாலும், கடலாற்றால் சூழப்பட்ட தட்டைப் புவியாலான எளிய அண்டப் படிமத்தை சுட்டுகின்றனர்." கிரேக்கர்களின் கண்ணோட்டப்படி, சில விண்மீன்கள் வானில் எழுந்து கடலில் வீழ்தலை/மறைதலைக் கூறியுள்ளனர்;மர்ரவிண்மீன்கள் ஆண்டின் சிலகாலங்களில்நிலமுனை சுற்றிவருகின்றன எனவும் மேலுஞ்சிலவோ கதிர் எழுச்சியிலோ கதிர்மறைவிலோ எழு அல்லத் மறையும் எனவும் கருதியுள்ளனர். கி.மு 5 ஆம், 6 ஆம் நூற்றாண்டுகளின் முந்து சாக்ரட்டிய மெய்யியலில் அண்டம் பற்றிய நோக்குகள் உள்ளன. அனாக்சிமாந்தர் (அண். கி.மு 610–அண். கி.மு546) அண்ட மையத்தில் தொங்கும் புவி நெருப்பு வலயங்களால் சூழ்ந்துள்ளதாக்க் குறிப்பிடுகிறார். விண்மீன்கள், கோள்கள், ஞாயிறு, திங்கள், புவி, எதிர்ப்புவி(Antichthon)—என ஆகமொத்தத்தில் பத்து வான்பொருள்கள்—கட்புலப்படாத மைய நெருப்பைச் சுற்றிவரும் அண்டப் படிமத்தைப் பிலோலாசு எனும் பித்தகோரியர் (அண். கி.மு 480- அண். கி.மு405) விவரித்துள்ளார். இவை கிரேக்கர்கள் கி.மு ஐந்தாம், ஆறாம் நூற்றாண்டுகளில் கோள்களைப் பற்றியும் அண்டக் கட்டமைப்பு பற்றியும் அறிந்திருந்தனர் என்பதை புலப்படுத்துகின்றன. தொடக்க காலக் கிரேக்க வானியலில் கோள்கள்கோள்கள் என்ற சொல் கிரேக்கச் சொல்லான πλανήτης (planētēs) என்பதில் இருந்து தோன்றியதாகும். இதன் பொருள் அலைவன என்பதாகும்..இவை விண்மீன்களோடு ஓப்பிடும்போது வானப்பரப்பில் இயங்குவதைக் கண்டதால் வானியலாளர்களால் இப்பெயரிடப்பட்ட்து. வெற்றுக்கண்ணால் அறிவன் (புதன்), வெள்ளி, செவ்வாய், வியாழன், காரி (சனி) ஆகிய ஐந்து கோள்களைக் காணலாம்: சில வேளைகளில்.கண்ணில் புலப்படு திங்களும் ஞாயிறும் கூட கோள்களாகக் கருதப்பட்டன. எனவே ஏழு கோள்களால் வாரக் கிழமைகளுக்குப் பெயரிடப்பட்டன. ஐந்து கோள்களும் அடிக்கடி ஞாயிற்றை நெருங்கும்போது மறைவதால் அவற்றை இனங்காணல் அரிய பணியாக இருந்த்து. வெள்ளியை நோக்குவதும் ஆய்வதும் நேரடியாக இயலாததாகும். தொடக்க கால கிரேக்கர்கள் மாலையிலும் காலையிலும் தோன்றும் வெல்லியைத் தனித்தனிக் கோளாக்க் கருதி அவற்றுக்கு எசுப்ரசு (மாலைமீன்) பாசுபெரசு (காலைமீன்) என இருபெயரிட்டுள்ளனர் பின்னரே அவை இரண்டும் ஒன்றே என்ற முடிவுக்கு வந்துள்ளனர். இதை அர்வித்த்து பித்தகோரசு எனக் கூறப்படுகிறது. கோள்கள் பிறகு கிரேக்கத் தொன்மங்களின் வழியாகப் பெயரிடப்பட்டுள்ளன. ஆனால் கோள்களுக்கான ஆங்கிலப் பெயர்கள் இணையான உரோமானியத் தொன்மங்களின் வழியாகப் பெயரிடப்பட்டன. கால அட்டவணைகள்பல பண்டைய கால அட்டவணைகள் சூரிய அல்லது நிலா வட்டிப்புகளை வைத்தே உருவாகின. எலனியக் கால அட்டவணையும் இவ்விரு வட்டிப்புகளையும் பயன்படுத்தியது. இருவட்டிப்புகளையும் உள்ளடக்கும் நிலாக் கால அட்டவணையை அமைத்தல் அரிது. சில கிரேக்க வானியலாளர்கள் வான்பொருள் ஒளிமறைப்பு வட்டிப்புகளை வைத்தும் கால அட்டவணையை உருவாக்கியுள்ளனர். யூடாக்சிய வானியல்செவ்வியல் காலக் கிரேக்கத்தில் வானியல் கணிதவியலின் ஒரு பிரிவாக விளங்கியது;வானியலாளர்கள் வான்பொருள் இயக்கங்களின் தோற்றங்களைக் கணிக்கும் வடிவியல் படிமங்களை உருவாக்கினர். இம்மரபு பிதாகோரசில் இருந்து தொடங்கியது. அவர் வானியலை நான்கு கணிதக்கலைகளில் ஒன்றாக வைத்தார். மற்ற மூன்று கணிதக்கலைகள் எண்ணியல், வடிவியல், இசை என்பனவாகும். இந்த நான்கு கலைகளைப் பற்றிய ஆய்வு நான்முகவியம் Quadrivium எனப்பட்டது. பிளாட்டோ (427–347 BC) கணிதவியல் ஆக்கப்பணியில் ஈடுபட்டவரல்ல என்றாலும், இவர் தன் மெய்யியல் கல்வியில் நான்முகவியத்தை கட்டாய அடிப்படைப் பாடப் பொருளாக்கினார். புத்தூழி அறிவியல் வரலாற்றாசிரியர் ஒருவர் கூற்றின்படி, David Lindberg இவர் இளங்கணிதவியல் அறிஞரான நீடியோசுவின் யூடாக்சிசு (அண்.கி.மு 410–அண்.கி.மு 347)கிரேக்க வானியலை வளர்த்தெடுக்க ஊக்கமூட்டினார்.
இருகோளப் படிமம் அண்டத்தை இரண்டாகப் பகுக்கும் புவிமையப் படிமமாகும். அவற்றில் ஒன்று மையத்தில் நிலவும் புவிக்கோளம் ஆகும். அடுத்தது இயக்கமற்ற நிலா மண்டலமாகும் இறுதியில் புவியை மையமாகக் கொண்ட விண்கோளமாகும். இதில் உள்ள பல சுழல்கோளங்கள் செவ்வியற்கால ஐம்பூதங்களில் ஒன்றான ஈதரால் ஆனவையாகக் கருதப்பட்டன]]. 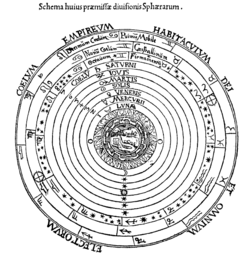 அண்டம் பற்றிய பிளாட்டோவின் முதன்மையான நூல்கள் Timaeus, Republic என்பனவாகும். இவற்றில் இருகோளப் படிமத்தை விவரிக்கிறார் இவர் கோள்களுக்கானஏழுகோளங்களையும் நிலை விண்மீன்கள் உள்ள விண்ணகத்துக்கான ஒரு கோளத்தையும் சேர்த்து மொத்தம் எட்டு கோளங்களாக அண்ட்த்தைப் பகுக்கிறார். குடியரசு நூலில் உள்ள ஏர் தொன்மத்தின்படி, அண்டம் தேவையெனும் பெண்கடவுளின் நூற்புக்கதிர் ஆகும். இது சைரன்களால் (தொன்மவியல்) காக்கப்படுகிறது. இந்தக் கதிர் தேவை எனும் பெண்கடவுளின் முறை அல்லது ஊழ் என ஒட்டுமொத்தமாகக் கூறப்படும் மூன்று பெண்களால் நூற்கப்படுகிறது. கி.பி ஆறாம் நூற்றாண்டில் வாழ்ந்த சிசிலியா நகரச் சிம்பிலிசியசுவின் ஒரு கதையின்படி, பிளாட்டோ தன்சம கால கணிதவியல் அறிஞர்களுக்கு பின்வரும் வினவலை எழுப்பியுள்ளார்: "சீரான, ஒழுங்குக்கு உட்பட்ட இயக்கங்கள் என்ற கருதலின்படி, கோள்களின் தோற்றங்களை எப்படி விளக்குவீர்கள்?" (quoted in Lloyd 1970, p. 84). மேலும் பிளாட்டோ, பார்க்கும்போது அலைந்து திரியும் கோள்களின் இயக்கங்களைத் திறம்பட, மையப் புவியைச் சுற்றி அமையும் சீரான வட்ட இயக்கத்தாலேயே, விளக்கமுடியும் என முன்மொழிந்துள்ளார். இது கி,பி 4 ஆம் நூற்றாண்டில் ஒரு புதிய எண்னக்கருவாகும் எனலாம். இதற்கு யூடாக்சிசு ஒருகோளுக்கொரு மையமொன்றிய கோளத்தையும் ஒவ்வொரு கோளத்துக்கும் வேறுவேறான சுழல்நேரத்தையும் ஒதுக்கித் தோராயமாக கோள்களின் தோற்றங்களை விளக்கித் தீர்வு கண்டார். எனவே கோள்களின் இயக்கங்களுக்கான கணிதவியல் விளக்கத்தை முதன்முதலாக உருவாக்கியவர் யூடாக்சிசே ஆவார். இவரது கோள்கள் பற்றிய நூலான On Speeds நூலின் பொதுவான எண்ணவோட்ட்த்தைப் பின்வரும் சுட்டல்களால் அறியலாம். அவை 1. அரிசுட்டாட்டிலின் Metaphysics XII, 8, 2. அரிசுட்டாட்டிலின் மற்றொரு நூலான De caelo நூலுக்கு சிம்பிலிசிசியசுவின் உரை என்பனவாகும். யூடாக்சுவின் அனைத்து நூல்களௌ அழிந்துவிட்ட்தால், யூடாக்சு பற்றிய அரிவு இரண்டாம் தவல்கள் வழியாகவே அறிய நேர்ந்துள்ளது. யூடாக்சுவின் கருத்தை விவரிக்கும் அராத்தசுவின் வானியல் கவிதை, மேலும் பிதினியா நகரத் தியோடோசியசுவின் கோளவியல் எனும் கவிதை ஆகியவையும் யூடாக்சுவின் கண்ணோட்டங்களை விவரிக்கின்றன. இவர்களே யூடாக்சுவின் கோள வானியலையும் கோள்களின் இயக்கங்களையும் சுட்டிக்காட்டி விளக்குகின்றனர். கி.பி 4 ஆம் நூற்றாண்டு கிரேக்க வானியலாளரான காலிப்பசு யுட்டாக்சுவின் 27 கோளங்களோடு மேலும் ஏழு கோளங்களைச் சேர்த்தார் (யூடாக்சசு கோள்களுக்கான கோளங்களோடு நிலைவிண்மீகளுக்காக ஒரு கோளத்தையும் இணைத்திருந்தார்). அரிசுட்டாட்டில் இருவகைகலையும் கூரிவிட்டு ஒவ்வொரு கோளங்களுக்கும் இடையில் ஒரு சுழலாத நிலைக்கோளத்தை வெளிக்கோள இயக்கம் மற்றதற்கு கடத்தப்படாமல் இருக்க, செருகினார். இவர் அமைப்பின் புரநிலைத் தன்மை பற்ரிக் கவலைப்பட்டார். நிலைக்கோளம் இல்லாவிடில் வெளிக்கோள இயக்கம் உட்கோளத்துக்குக் கட்த்தப்படும். எலனிய வானியல்கோள்படிமங்களும் நோக்கீட்டு வானியலும்யூடாக்சசு வானியல் படிமத்தில் சில அடிப்படை குறைபாடுகள் உள்ளன. முதலாவதாக, இதனால் துல்லியமாக இயக்கங்களை கணிக்கமுடியவில்லை.இந்தக் குறைகள்aiகாலிப்பசு நூல் திருத்த முயல்கிறது. அடுத்தச் சிக்கல், இவரது படிமங்களால் கோள்களின் தோற்றநிலை வேகமாற்றத்தை விளக்க இயலாமை ஆகும். மூன்றாம் குறைபாடு புவியில் இருந்து பார்க்கும்போது மாறும் கோள்களின் பொலிவு மாற்றத்தை இப்படிமங்களால் விளக்க இயலாமையாகும். கோள்கள் உள்ள கோளங்கள் புவியில் இருந்து சம தொலைவிலேயே அமைதலால் அல்லது புவிமையம் ஒன்றியவையாக உள்ளதால், இவற்ரின் பொலிவு மாறக்கூடாது. இச்சிக்கலி பிதனேவின் ஆத்தோலிக்கசு கி.மு 310 இலேயே சுட்டிக் காட்டியுள்ளார். இதற்காக பெர்காவின் அப்பொல்லோனியசு (அண். கி.மு 262 –அண். கி.மு 190) இரண்டு இயஙுமுறைகளை அறிமுகப்படுத்தினார். இது கோள்களின் தொலைவு மாற்றத்தையும் வேக மாற்றத்தையும் விளக்க முயன்றது:இவை மையவிலகு ஊர்தி, ஊர்தியும் புறஞ்சுழல்வும் என்பனவாகும். ஊர்தி என்பது புவியைச் சுற்றி கோலைக் கொண்டுசெல்லும் வட்டமாகும். எனவே மையவிலகு ஊர்தி என்பது புவியில் இருந்து சற்றே விலகிய மையமுள்ள உருளியாகும். மையவிலகு உருளி, புறஉருளி படிமத்தில், முன்னது சிறுவட்டத்தை ஏந்தும். புற உருளியோ கோளை ஏந்திச் செல்லும். எனவே இப்படிமம் அப்பொல்லோனியசு தேற்றத்தின்படி கோளியக்கத்தை ஒப்புருவாக்கிக் காட்டும். இது தோற்றப் பின்னேகும் இயக்கத்தையும் கூட விளக்கும் which happens when planets appear to reverse their motion through the zodiac for a short time. புத்தூழி வானியல் வரலாற்றாசிரியர்கள் யூடாக்சசுவின் படிமம் சில கோள்களுக்கு மட்டுமே மிகத் தோராயமாகவே பின்னேகும் இயக்கத்தை விளக்கியிருக்கும் எனவும் மற்றவற்றுக்குப் பொருந்த வாய்ப்பில்லை எனவும் கருதுகின்றனர். கி.மு இரண்டாம் நூற்றாண்டில் ஃஇப்பார்க்கசு பாபிலோனிய வானியலாளர்கள் கோள்களின் இயக்கத்தை மிகத் துல்லியமாக முன்கணிப்பதை அறிந்திருந்தார், இதே அளவு துல்லியத்தை கிரேக்க வானியலாளர்களும் அடையவேண்டும் என வற்புறுத்தினார்.அவருக்கு பாபிலோனிய வானியல் நோக்கீடுகளுடனும் முன்கணிப்புடனும் தொடர்புகொண்டு இருந்ததால், அவற்றைப் பயன்படுத்தி சிறந்த படிமங்களை உருவாக்க முயன்றார். சூரிய இயக்கத்துக்கு சமப் பகலிரவுப் புள்ளிகளைப் பயன்படுத்தி இவர் ஓர் எளிய மையவிலகு படிமத்தைப் பயன்படுத்தினார். இது எளிதாக சூரியனின் வேக மாற்றத்தையும் பருவ கால இடைவெளி மாற்றத்தையும் விளக்கியது. நிலா அல்லது திங்களுக்கு, இவர் அப்பொல்லோனியசு தேற்றத்தின்படி, மையவிலகு உருளி, புற உருளி படிமத்தைப் பயன்படுத்தினார. மற்ர கோள்களுக்கு இவரால் துல்லியமான படிமம் ஏதும் உருவாக்க இயலவில்லை. ஆனால் கிரேக்க் வானியலாரின் துல்லியமற்ற படிமங்களைக் குறைகூறினார். ஃஇப்பார்க்கசு விண்மீன்களுக்கான அட்டவணையொன்றையும் தொகுத்தார். பிளினி முதுவல் கருத்துப்படி, இப்பார்க்கசு புது விண்மீனையும் (Nova) கண்டுள்ளார். இவர் விண்மீன்களின் இருப்புகளையும் பொலிவு மதிப்புகளையும் பதிவு செய்துள்ளார். இதனால் பிவந்த தலைமுறையினர் வின்மீன்கள் உருவாகின்ரனவா, அழிகின்றனவா, இடம் பெயர்ந்துள்ளனவா,அல்லது பொலிவு மாற்றம் பெற்றுள்ளனவா எனச் சொல்ல முடிந்தது. தாலமி இப்பார்க்கசு புவியின் தலையாட்டத்தைக் (அச்சலைவைக்) கண்டுபிடித்ததைக் குறிப்பிடுபோது இந்த அட்டவணை பற்றிச் சுட்டுகிறார் இந்தப் புவியின் தலையாட்டம் புவியச்சு சற்றே இடம்பெயர்வதால் உருவாகிறது. இதனால் சமப் பகலிரவுப் புள்ளிகளும் மெல்ல இடமாறுகின்றன. இந்நிகழ்வு நிலைவிண்மீன்கள் உள்ல கோளச் சுழற்சியால் விளைவதாக இப்பார்க்கசு கருதியுள்ளார். சூரியமையப் படிமமும் அண்ட அளவுகோல்களும்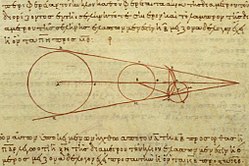 கி.மு 3 ஆம் நூற்றாண்டில் சாமோசுவின் அரிசுடார்க்கசு மாற்று அண்டவியலை, அதாவது மாற்றுப் புடவி அமைப்பை அறிமுகப்படுத்தினார். இது சூரியமைய சூரியக் குடும்பம் எனப்பட்டது. இதில் புவிக்கு மாற்றாக, சூரியன் அண்ட மையத்தில் அமைந்தது(எனவே இவர் சிலவேளைகளில் கிரேக்கக் கோப்பர்னிக்கசு எனப்படுகிறார்). இவரது வானியல் கருத்துகள் பரவலாக ஏற்கப்படவில்லை. என்றாலும் ஒருசில மேற்கோள்கள் எஞ்சியுள்ளன. இவரது மாணாக்கராக செலியூசியா நகரச் செலியூக்கசுவை அறிவோம். இவர் சூரியன். திங்கள் இடையிலான தொலைவுகளையும் அளவுகளையும் பற்றி எனும் நூலை இயற்றியுள்ளார். இது இப்போது கிடைக்கிறது. இந்நூலில் இவர் புவியில் இருந்துள்ள சூரியன், திங்கள் ஆகிய இரண்டின் அளவுகளையும் அவற்றின் தொலைவுகளையும் புவியின் ஆரங்களில் கணக்கிட்டுள்ளார். சிறிது காலத்துக்குப் பின்னர் எராடோதீனெசு புவியின் அளவைக் கணக்கிட்டுள்ளார். இதனால் இவர், அரிசுடார்க்கசுவின் கணக்கீடுகளில் புவியாரத்தைப் பதிலிட்டு உண்மை மதிப்புகலை அடைய வழிவகுத்தார். இப்பார்க்கசுவும் சூரியன், திங்கள் அளவுகளும் தொலைவுகளும் என்று மற்றொரு நூலை இயற்றியுள்ளார், ஆனால் இந்நூல் இப்போது கிடைக்கவில்லை. அரிசுட்டார்க்கசு, இப்பார்க்கசு ஆகிய இருவருமே புவியில் இருந்துள்ள சூரியனின் தொலைவை மிகவும் குறைவாகவே மதிப்பிட்டுள்ளனர். கிரேக்க- உரோமானிய கால, பிற்பண்டைய கால வானியல்ஃஇப்பார்க்கசு வானியலில் துல்லியமான முன்கணிப்புகளுக்கு வழிவகுத்ததால், கிரேக்க வானியலாளர்களில் முதன்மையானவராக்க் கருதப்படுகிறார் மேலும் இவரே கி.பி இரண்டாம் நூற்றாண்டில் உரோமானிய எகிப்தில் அலெக்சாந்திரியாவில் வாழ்ந்த கணிதவியலாளரான கிளாடியசுவுக்கு முந்திய புதுமைவாய்ந்த இறுதி கிரேக்க வானியலாளராகவும் கருதப்படுகிறார். தாலமியின் வானியல், கணியவியல் (சோதிடம்) சார்ந்த நூல்களில் Almagest (அல்மகெசுட்டு), Planetary Hypotheses ( கோளியல் கருதுகோள்கள்), Tetrabiblos, Handy Tables (கையடக்கப் பட்டியல்கள்), Canobic Inscription' ஆகியவையும் மேலுஞ்சில சிறுநூல்களும் உள்ளடங்கும். தாலமிய வானியல்மேலை வானியல் வரலாற்றிலேயே மிகவும் தாக்கஞ்செலுத்திய நூல் அல்மகெசுட்டு ஆகும். இந்நூலில் தாலமி கோல்களின் நடத்தைகளை எப்படி முன்கணிப்பது என விளக்கியுள்ளார். இப்பார்க்கசுவால் இதைச் சமனியம் (Equant) எனும் கணிதக் கருவியைப் பயன்படுத்தியும் நிறைவேற்ற இயலவில்லை. அல்மகெசுட்டு வானியலை, முந்தைய கணிதவியலாளர்களின் தேற்றங்களையும் படிமங்களையும் நோக்கிடுகளையும் பயன்படுத்தி, எளிமையாக விளக்கியது. இதனாலேயே மற்ற சிறப்பான துறை நூல்கள் புறக்கணிது ஒதுக்கப்பட,இதுமட்டும் நின்றுநிலவலானது.எனவேதான் சூரியமைய அமைப்பாலும் டைக்கோவின் அமைப்பாலும் பதிலீடு செய்யப்படுவரை, தாலமியின் கீழ்வரும் செந்தரக் கோள்களின் வரிசை மாற்றப்படவேயில்லை :
தாலமியின் கனிதவியலாளர்பாலான சார்பு, குறிப்பாக இப்பார்க்கசுவின் விண்மீன்களின் அட்டவணை மீதான சார்பு 19 ஆம் நூற்றாண்டு முதலே விவாதம் செய்யப்படுகிறது. இராபர்ட் ஆர். நியூட்டன் 1970களில் முரண்பாடான கருத்தோட்டம் முன்வைக்கப்பட்டது. அவரது நூலான The Crime of Claudius Ptolemy என்ற நூலில் பின்வருமாறு விவாதீக்கிறார். தாலமி தன் நோக்கீடுகளை தவறாகப் போலிசெய்து இப்பார்க்கசுவின் விண்மீன்களின் அட்டவணையைத் தனதாகத் தப்பாகக் கூறுகிறார். ஆனால், இதை மற்ற வானியல் வரலாற்றாளர்கள் ஏற்கவில்லை. பிந்தைய பண்டைக்கால கணிதவியலாளர்கள் தாலமியின் அல்மகெசுட்டு நூலுக்கு உரை எழுதியுள்ளனர். இவர்களில் அலெக்சாந்திரியாவின் பாப்பசுவும் தியோனும் பின்னவரின் மகளான கைபேசியாவும் அடங்குவர்.தாலமியின் வானியல் இடைக்கால ஐரோப்பிய வானியலிலும் இசுலாமிய வானியலிலும் 16 ஆம் நூற்றாண்டில் சூரிய மைய வானியலை மரகான் வான்காணகம் அறிமுகப்படுத்தும் வரையிலும் டைக்கோவின் வானியல் கண்ணோட்டம் ஏற்கப்படும் வரையிலும் செந்தர வடிவமாக ஏற்றுக்கொள்ளப்பட்டது.என்றாலும் அண்மையில் கண்டறியப்பட்ட கையெழுத்துப்படிகள் பண்டைய கிரேக்க கணியவியலாளர்கள் தாலமிக்கு முந்தைய வானியலை நடைமுறையில் பின்பற்றியதைக் காட்டுகின்றன (Aaboe, 2001). இந்திய வானியலின்பாலான தாக்கம் கிரேக்க வானியல் இந்தியாவுக்கு அண்மையில் உள்ள கிரேக்க பாக்தீரிய நாட்டு நகரமான அல்கவுனமில் கி.மு 3 ஆம் நூற்றாண்டில் இருந்த் நடைமுறையில் இருந்ததாகக் கூறப்படுகிறது. நில நடுவரை சூரியக்கடிகை உட்பட்ட பல சூரியக்கடிகைகள் உஜ்ஜைன் நகர அகலாங்குக்கு சரிசெய்யப்பட்டு வந்தமை அவ்விடத்துத் தொல்லியல் ஆகழ்வுகளால் தெரிய வந்துள்ளது.[4] இக்கால கட்டத்தில் மவுரியப் பேரரசுடனான ஊடாட்டங்களாலும் பின்விளைந்த இந்தோ-கிரேக்க ஆட்சி விரிவாலும் இந்தியாவில் கிரேக்க வானியல் பரவியிருக்கலாம் எனக் கருதப்படுகிறது.[5] மேலும் கி.பி முதலிரு நூற்றாண்டுகளில் எலனிய வானியல் சார்ந்த கணியவியல் நூல்கள் இந்தியாவுக்கு இறக்குமதி ஆகியுள்ளன. யவனக் கணியவியல் Yavanajataka எனும் நூல் கிரேக்கத்தில் இருந்து சமக்கிருத மொழிக்கு கி.பி 2 ஆம் நூற்றாண்டில் யவனேசுவரரால் மொழிபெயர்க்கப் பட்டுள்ளது, இது மேலைச் சாகா அரசன் உருத்திராடமன் உதவியால் மேற்கொள்ளப்பட்டுள்ளது. இவ்வரசனின் தலைநகர் உஜ்ஜயினி ஆகும். உஜ்ஜயினி இந்திய கிரீன்விச்சாக அந்நாளில் இந்திய வானியலாளர்களாலும் அரபுநாட்டு ஆரினாலும் இலத்தீன் நூல்களாலும் கருதப்பட்டுள்ளது.ஏனெனில் இவந்தான் இந்தியாவில் கிரேக்க வானியலும் கணியவியலும் ஊக்கமூட்டி அறிமுகப்படுத்தப்பட்டுள்ளன."[6] பிறகு கி.பி ஆறாம் நூற்றாண்டில், Romaka Siddhanta ("உரோம நெறிமுறைகள்"), Paulisa Siddhanta ("பவுலிய நெறிமுறைகள்]]") ஆகிய இருநூல்களை உள்ளக்கி Pañca-siddhāntikā ("ஐந்தொகை நூல்கள்") என்ற நூலில் கிரேக்க, எகிப்திய, எலனிய, இந்திய வானியல் அறிவைத் தொகுத்தளித்தார்.[7] வராகமித்திரர் தனது பிரிகத் சங்கிதை எனும் நூலில் பின்வருமாறு எழுதுகிறார். கிரேக்கர்கள் அயல்நாட்டவர்கள். அவர்களிடம் இந்த அறிவியல் நன்கு நிறுவப்பட்டுள்ளது. அவர்கள் முனிவர்களாக மதிக்கப்பட்டாலும், இந்த வான் அறிவியலறிந்தவர் ஒருவர் சரியாகவோ தவறாகவோ இருமுறை பிறந்தவராகக் கருதப்படுகிறார்."[8] கிரேக்க வானியலுக்கான தகவல் வாயில்கள்பல கிரேக்க வானியல் நூல்களின் பெயர்கள் மட்டுமே நிலவுகின்றன. இவையும் விவரிப்புகளாலோ மேற்கோள்களாலோ மட்டுமே கிடைத்துள்ளன. சில கணித இயல்பற்ற பள்ளி நூல்கள் மட்டுமே அவற்றின் தொடர்பயன்பாடு காரணமாக்க் கிடைத்துள்ளன.இவற்றுள் யூக்ளீடி நிகழ்வுகள் (Phaenomena), பிதேன் நகரத்தின் ஆதோலிக்கசுவின் இருநூல்களும் அடங்கும்.மேலும் தாலமிக்கு முன் கிளியோமெடெசு, கெமினெசு, சுமிர்னாவின் தியோன் ஆகியவர்களால் எழுதப்பட்ட மூன்று பாட நூல்கள் கிடைத்துள்ளனமெலும் உரொமானிய எழுத்தாளர்களான பிளினி முதுவலும் வித்ரூவியசும் கிரேக்க வானியலின் சில தகவல்களைத் தருகின்றனர். மிக முதன்மையான நூல் அல்மகுசுட்டு எனும் நூலே ஆகும். இதில் தாலமி தனக்கு முந்தைய பல நூல்களை மேற்கோள்களாக்க் காட்டுகிறார் (Evans 1998, p. 24). பெயர்பெற்ற பண்டைய வானியலாளர்கள்கட்டுரையில் உள்ள வானியலாளர்களைத் தவிர பின்வருபவர்களும் கணித வானியலுக்கு அல்லது அண்டவியலுக்குப் பங்களிப்பு செய்துள்ளனர்.
குறிப்புகள்
மேற்கோள்கள்
வெளி இணைப்புகள் |
Portal di Ensiklopedia Dunia













