Я«хЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«фЯ»ЇЯ«фЯ»ђЯ«ЪЯ«┐Я«»Я«Й:Я«цЯ««Я«┐Я«┤Я»Ї Я«хЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я»ѓЯ«ЪЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»ѕЯ«»Я»ЄЯ«ЪЯ»Ђ/Я«хЯ»ЄЯ«цЯ«┐Я«»Я«┐Я«»Я«▓Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ«БЯ«┐Я«ц Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕЯ«џЯ»Ї Я«џЯ»ЄЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«▓Я»Ї Я«хЯ»ЄЯ«цЯ«┐Я«»Я«┐Я«»Я«▓Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ«БЯ«┐Я«цЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕ Я«ЁЯ«цЯ«▒Я»ЇЯ«ЋЯ»ЂЯ«░Я«┐Я«» Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«фЯ»Ї Я«фЯ«цЯ«┐Я«хЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«хЯ«цЯ»Ђ Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«░Я»Ї Я«ЁЯ«цЯ«ЕЯ»ѕ Я««Я»ЄЯ««Я»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«цЯ«▓Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«фЯ«БЯ«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«▓Я«ЋЯ»ЂЯ«хЯ«ЙЯ«ЕЯ«цЯ»Ђ.
Я«ЋЯ«БЯ«┐Я«цЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї
Я«ЋЯ«БЯ«┐Я«цЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я»ђЯ«ЪЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї
 Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
<math> f(x) = x^2\,\!</math> Я«јЯ«Е Я«ЅЯ«│Я»ЇЯ«│Я»ђЯ«ЪЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«хЯ«цЯ«ЕЯ»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«ЋЯ«┐Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
 , ,  Я««Я»ЂЯ«цЯ«▓Я«ЙЯ«Е Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«цЯ«▓Я«ЙЯ«Е Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї
<math>\sqrt{1-e^2}</math>, <math>\sqrt{1-z^3}</math> Я«јЯ«Е Я«ЅЯ«│Я»ЇЯ«│Я»ђЯ«ЪЯ»Ђ Я««Я»ѓЯ«▓Я««Я»Ї Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї.
- Я«џЯ«┐Я«▓ Я«џЯ«┐Я«▒Я«фЯ»ЇЯ«фЯ«ЙЯ«Е Я«јЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ѕ Я«фЯ«цЯ«┐Я«» Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я««Я»ЂЯ«▒Я»ѕ
| Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я«┐Я«ЪЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕ
|
Я«цЯ»ІЯ«▒Я»ЇЯ«▒Я««Я»Ї
|
α β γ δ ε ζ
η θ ι κ λ μ ν
ξ ο π ρ σ ς
τ υ φ χ ψ ω
|
╬▒ ╬▓ ╬│ ╬┤ ╬х ╬Х
╬и ╬И ╬╣ ╬║ ╬╗ ╬╝ ╬й
╬Й ╬┐ ¤ђ ¤Ђ ¤Ѓ ¤ѓ
¤ё ¤Ё ¤є ¤Є ¤ѕ ¤Ѕ
|
Γ Δ Θ Λ Ξ Π
Σ Φ Ψ Ω
|
╬Њ ╬ћ ╬ў ╬Џ ╬ъ ╬а
╬Б ╬д ╬е ╬Е
|
∫ ∑ ∏ √ − ± ∞
≈ ∝ {{=}} ≡ ≠ ≤ ≥
× · ⋅ ÷ ∂ ′ ″
∇ ‰ ° ∴ ∅
|
РѕФ РѕЉ РѕЈ Рѕџ Рѕњ ┬▒ Рѕъ
РЅѕ РѕЮ = РЅА РЅа РЅц РЅЦ
├Ќ ┬и РІЁ ├и Рѕѓ Рђ▓ Рђ│
РѕЄ Рђ░ ┬░ Рѕ┤ РѕЁ
|
∈ ∉ ∩ ∪ ⊂ ⊃ ⊆ ⊇
¬ ∧ ∨ ∃ ∀
⇒ ⇔ → ↔ ↑ ↓
ℵ - – —
|
Рѕѕ РѕЅ РѕЕ Рѕф Ріѓ РіЃ Ріє РіЄ
┬г РѕД Рѕе РѕЃ Рѕђ
РЄњ РЄћ Рєњ Рєћ РєЉ РєЊ
Рёх - РђЊ Рђћ
|
Я«еЯ«┐Я«»Я««Я«ЋЯ»Ї Я«ЋЯ«БЯ«┐Я«цЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕ Я«єЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ«▓Я»Ї
| Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я«┐Я«ЪЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕ
|
Я«цЯ»ІЯ«▒Я»ЇЯ«▒Я««Я»Ї
|
\exp_a b = a^b, \exp b = e^b, 10^m
|

|
\ln c, \lg d = \log e, \log_{10} f
|

|
\sin a, \cos b, \tan c, \cot d, \sec e, \csc f
|

|
\arcsin h, \arccos i, \arctan j
|

|
\sinh k, \cosh l, \tanh m, \coth n
|

|
\operatorname{sh}\,k, \operatorname{ch}\,l, \operatorname{th}\,m, \operatorname{coth}\,n
|

|
\operatorname{argsh}\,o, \operatorname{argch}\,p, \operatorname{argth}\,q
|

|
\sgn r, \left\vert s \right\vert
|

|
\min(x,y), \max(x,y)
|

|
Я«ЁЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ«┐Я«цЯ«џЯ»Ї Я«џЯ»єЯ«»Я«▒Я»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї
Я«ЁЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ«┐Я«цЯ«џЯ»Ї Я«џЯ»єЯ«»Я«▒Я»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я«ЙЯ«Е ![{\displaystyle \surd ,{\sqrt {2}},{\sqrt[{n}]{}},{\sqrt[{3}]{x^{3}+y^{3} \over 2}}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9d0eb602bb67c297148e7454c160c7750cf84d7) Я«јЯ«ЕЯ»ЇЯ«фЯ«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒ Я«јЯ«ЕЯ»ЇЯ«фЯ«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒
- <math>\surd, \sqrt{2}, \sqrt[n]{}, \sqrt[3]{x^3+y^3 \over 2}\!</math> Я«јЯ«Е Я«ЅЯ«│Я»ЇЯ«│Я»ђЯ«ЪЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«» Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї.
Я«хЯ«ЋЯ»ѕЯ«»Я»ђЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ«░Я»ЂЯ«хЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї
| Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я«┐Я«ЪЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕ
|
Я«цЯ»ІЯ«▒Я»ЇЯ«▒Я««Я»Ї
|
dt, \operatorname{d}\!t, \partial t, \nabla\psi
|

|
dy/dx, \operatorname{d}\!y/\operatorname{d}\!x, {dy \over dx}, {\operatorname{d}\!y\over\operatorname{d}\!x}, {\partial^2\over\partial x_1\partial x_2}y
|

|
\prime, \backprime, f^\prime, f', f'', f^{(3)}, \dot y, \ddot y
|

|
|
|
Я«ЋЯ«БЯ««Я»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«еЯ»ЇЯ«ц Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї
| Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я«┐Я«ЪЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕ
|
Я«цЯ»ІЯ«▒Я»ЇЯ«▒Я««Я»Ї
|
\{ \}, \O \empty \emptyset, \varnothing
|

|
\in, \notin \not \in, \ni, \not\ni
|

|
\cap, \Cap, \sqcap, \bigcap
|

|
\cup, \Cup, \sqcup, \bigcup, \bigsqcup, \uplus, \biguplus
|

|
\setminus, \smallsetminus, \times
|

|
\subset, \Subset, \sqsubset
|

|
\supset, \Supset, \sqsupset
|

|
\subseteq, \nsubseteq, \subsetneq, \varsubsetneq, \sqsubseteq
|

|
\supseteq, \nsupseteq, \supsetneq, \varsupsetneq, \sqsupseteq
|

|
\subseteqq, \nsubseteqq, \subsetneqq, \varsubsetneqq
|

|
\supseteqq, \nsupseteqq, \supsetneqq, \varsupsetneqq
|

|
|
|
Я«еЯ»ђЯ«│Я««Я«ЙЯ«Е Я«ЋЯ«БЯ«┐Я«ц Я«хЯ«┐Я«фЯ«░Я«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї
Я««Я»ЄЯ«▓Я»іЯ«ЪЯ»ЇЯ«ЪЯ»Ђ, Я«ЋЯ»ђЯ«┤Я»іЯ«ЪЯ»ЇЯ«ЪЯ»Ђ, Я«цЯ»іЯ«ЋЯ»ѕЯ«»Я«┐Я«ЪЯ«▓Я»Ї
| Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ |
Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ»Ђ |
Я«цЯ»ІЯ«▒Я»ЇЯ«▒Я««Я»Ї
|
| Я««Я»ЄЯ«▓Я»іЯ«ЪЯ»ЇЯ«ЪЯ»Ђ
|
a^2 |

|
| Я«ЋЯ»ђЯ«┤Я»іЯ«ЪЯ»ЇЯ«ЪЯ»Ђ
|
a_2 |

|
| Grouping
|
10^{30} a^{2+2} |

|
a_{i,j} b_{f'} |

|
| Combining sub & super without and with horizontal separation
|
x_2^3 |

|
{x_2}^3 |

|
| Super super
|
10^{10^{8}} |

|
| Preceding and/or additional sub & super
|
\sideset{_1^2}{_3^4}\prod_a^b |

|
{}_1^2\!\Omega_3^4 |

|
| Stacking
|
\overset{\alpha}{\omega} |

|
\underset{\alpha}{\omega} |

|
\overset{\alpha}{\underset{\gamma}{\omega}} |

|
\stackrel{\alpha}{\omega} |

|
| Derivatives
|
x', y'', f', f'' |

|
x^\prime, y^{\prime\prime} |

|
| Derivative dots
|
\dot{x}, \ddot{x} |

|
| Underlines, overlines, vectors
|
\hat a \ \bar b \ \vec c |

|
\overrightarrow{a b} \ \overleftarrow{c d} \ \widehat{d e f} |

|
\overline{g h i} \ \underline{j k l} |

|
| Arc (workaround)
|
\overset{\frown} {AB} |

|
| Arrows
|
A \xleftarrow{n+\mu-1} B \xrightarrow[T]{n\pm i-1} C |
![{\displaystyle A{\xleftarrow {n+\mu -1}}B{\xrightarrow[{T}]{n\pm i-1}}C}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0645e6df7ace8a40eba2d92f293f5fbd6f929411)
|
| Overbraces
|
\overbrace{ 1+2+\cdots+100 }^{5050} |

|
| Underbraces
|
\underbrace{ a+b+\cdots+z }_{26} |

|
| Sum
|
\sum_{k=1}^N k^2 |

|
Sum (force \textstyle)
|
\textstyle \sum_{k=1}^N k^2 |

|
Sum in a fraction (default \textstyle)
|
\frac{\sum_{k=1}^N k^2}{a} |

|
Sum in a fraction (force \displaystyle)
|
\frac{\displaystyle \sum_{k=1}^N k^2}{a} |

|
| Sum in a fraction (alternative limits style)
|
\frac{\sum\limits^{^N}_{k=1} k^2}{a} |

|
| Product
|
\prod_{i=1}^N x_i |

|
Product (force \textstyle)
|
\textstyle \prod_{i=1}^N x_i |

|
| Coproduct
|
\coprod_{i=1}^N x_i |

|
Coproduct (force \textstyle)
|
\textstyle \coprod_{i=1}^N x_i |

|
| Limit
|
\lim_{n \to \infty}x_n |

|
Limit (force \textstyle)
|
\textstyle \lim_{n \to \infty}x_n |

|
| Integral
|
\int\limits_{1}^{3}\frac{e^3/x}{x^2}\, dx |

|
| Integral (alternative limits style)
|
\int_{1}^{3}\frac{e^3/x}{x^2}\, dx |

|
Integral (force \textstyle)
|
\textstyle \int\limits_{-N}^{N} e^x\, dx |

|
Integral (force \textstyle, alternative limits style)
|
\textstyle \int_{-N}^{N} e^x\, dx |

|
| Double integral
|
\iint\limits_D \, dx\,dy |

|
| Triple integral
|
\iiint\limits_E \, dx\,dy\,dz |

|
| Quadruple integral
|
\iiiint\limits_F \, dx\,dy\,dz\,dt |

|
| Line or path integral
|
\int_{(x,y)\in C} x^3\, dx + 4y^2\, dy |

|
| Closed line or path integral
|
\oint_{(x,y)\in C} x^3\, dx + 4y^2\, dy |

|
| Intersections
|
\bigcap_{i=_1}^n E_i |

|
| Unions
|
\bigcup_{i=_1}^n E_i |

|
Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї, Я«цЯ«ЙЯ«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї, Я«фЯ«ЕЯ»ЇЯ««Я«ЪЯ»ЇЯ«ЪЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї
| Я«хЯ«┐Я«хЯ«░Я««Я»Ї
|
Я«цЯ»іЯ«ЪЯ«░Я««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ
|
Я«цЯ»ІЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ«┐Я«цЯ««Я»Ї
|
| Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї
|
\frac{2}{4}=0.5 or {2 \over 4}=0.5
|

|
| Я«џЯ«┐Я«▒Я»Ђ Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї
|
\tfrac{2}{4} = 0.5
|

|
| Я«фЯ»єЯ«░Я»ЂЯ««Я»Ї (Я«ЄЯ«»Я«▓Я»ЇЯ«еЯ«┐Я«▓Я»ѕ) Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї
|
\dfrac{2}{4} = 0.5 \qquad \dfrac{2}{c + \dfrac{2}{d + \dfrac{2}{4}}} = a
|

|
| Я«фЯ»єЯ«░Я»ЂЯ««Я»Ї (Я«ЅЯ«ЪЯ»ЇЯ«фЯ»іЯ«цЯ«┐Я«хЯ»Ђ) Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї
|
\cfrac{2}{c + \cfrac{2}{d + \cfrac{2}{4}}} = a
|

|
| Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«еЯ»ђЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї
|
\cfrac{x}{1 + \cfrac{\cancel{y}}{\cancel{y}}} = \cfrac{x}{2}
|

|
| Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»Ї
|
\binom{n}{k}
|

|
| Я«џЯ«┐Я«▒Я»Ђ Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»Ї
|
\tbinom{n}{k}
|

|
| Я«фЯ»єЯ«░Я»Ђ (Я«ЄЯ«»Я«▓Я»ЇЯ«еЯ«┐Я«▓Я»ѕ) Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»Ї
|
\dbinom{n}{k}
|

|
| Я«ЁЯ«БЯ«┐Я«ЋЯ«│Я»Ї
|
\begin{matrix}
x & y \\
z & v
\end{matrix}
|

|
\begin{vmatrix}
x & y \\
z & v
\end{vmatrix}
|

|
\begin{Vmatrix}
x & y \\
z & v
\end{Vmatrix}
|

|
\begin{bmatrix}
0 & \cdots & 0 \\
\vdots & \ddots & \vdots \\
0 & \cdots & 0
\end{bmatrix}
|

|
\begin{Bmatrix}
x & y \\
z & v
\end{Bmatrix}
|

|
\begin{pmatrix}
x & y \\
z & v
\end{pmatrix}
|

|
\bigl( \begin{smallmatrix}
a&b\\ c&d
\end{smallmatrix} \bigr)
|

|
| Case distinctions
|
f(n) =
\begin{cases}
n/2, & \text{if }n\text{ is even} \\
3n+1, & \text{if }n\text{ is odd}
\end{cases}
|

|
| Я«фЯ«▓Я»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї
|
\begin{align}
f(x) & = (a+b)^2 \\
& = a^2+2ab+b^2 \\
\end{align}
|

|
\begin{alignat}{2}
f(x) & = (a-b)^2 \\
& = a^2-2ab+b^2 \\
\end{alignat}
|

|
| Я«фЯ«▓Я»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї (Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«еЯ«┐Я«░Я«▓Я»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ ({lcr}) Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«Ъ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї. (Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«┐Я«ЕЯ»ЇЯ«▒Я«┐ Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ«ЙЯ«цЯ»Ђ)
|
\begin{array}{lcl}
z & = & a \\
f(x,y,z) & = & x + y + z
\end{array}
|

|
| Я«фЯ«▓Я»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ (Я««Я»ЄЯ«▓Я«цЯ«┐Я«ЋЯ««Я»Ї)
|
\begin{array}{lcr}
z & = & a \\
f(x,y,z) & = & x + y + z
\end{array}
|

|
| Breaking up a long expression so that it wraps when necessary, at the expense of destroying correct spacing
|
<math>f(x) \,\!</math>
<math>= \sum_{n=0}^\infty a_n x^n </math>
<math>= a_0+a_1x+a_2x^2+\cdots</math>
|
  
|
| Simultaneous equations
|
\begin{cases}
3x + 5y + z \\
7x - 2y + 4z \\
-6x + 3y + 2z
\end{cases}
|

|
| Arrays
|
\begin{array}{|c|c||c|} a & b & S \\
\hline
0&0&1\\
0&1&1\\
1&0&1\\
1&1&0\\
\end{array}
|

|
Я«џЯ«┐Я«▓ Я«ЋЯ«БЯ«┐Я«цЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕ Я«јЯ«┤Я»ЂЯ«цЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«▒Я»ѕ
Я«ЄЯ«░Я»ЂЯ«фЯ«ЪЯ«┐Я«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒
<math>ax^2 + bx + c = 0</math>
 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒
<math>x={-b\pm\sqrt{b^2-4ac} \over 2a}</math>
Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«хЯ«▓Я»ЂЯ«хЯ«│Я«хЯ»ЂЯ««Я»Ї
 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒
<math>2 = \left(
\frac{\left(3-x\right) \times 2}{3-x}
\right)</math>
 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒
<math>S_{\text{new}} = S_{\text{old}} - \frac{ \left( 5-T \right) ^2} {2}</math> Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒
<math>S_{\text{new}} = S_{\text{old}} - \frac{ \left( 5-T \right) ^2} {2}</math>
Я«цЯ»іЯ«ЋЯ»ѕЯ«»Я»ђЯ«ЪЯ»Ђ
 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒
<math>\int_a^x \!\!\!\int_a^s f(y)\,dy\,ds
= \int_a^x f(y)(x-y)\,dy</math>
Я«цЯ«ЙЯ«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї

<math>\det(\mathsf{A}-\lambda\mathsf{I}) = 0</math>
Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї

<math>\sum_{i=0}^{n-1} i</math>

<math>\sum_{m=1}^\infty\sum_{n=1}^\infty\frac{m^2\,n}
{3^m\left(m\,3^n+n\,3^m\right)}</math>
Я«хЯ«ЋЯ»ѕЯ«»Я»ђЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ

<math>u'' + p(x)u' + q(x)u=f(x),\quad x>a</math>
Я«џЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї

<math>|\bar{z}| = |z|,
|(\bar{z})^n| = |z|^n,
\arg(z^n) = n \arg(z)</math>
Я«јЯ«▓Я»ЇЯ«▓Я»ѕЯ«ЋЯ«│Я»Ї

<math>\lim_{z\rightarrow z_0} f(z)=f(z_0)</math>
Я«цЯ»іЯ«ЋЯ»ѕЯ«»Я»ђЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
![{\displaystyle \phi _{n}(\kappa )={\frac {1}{4\pi ^{2}\kappa ^{2}}}\int _{0}^{\infty }{\frac {\sin(\kappa R)}{\kappa R}}{\frac {\partial }{\partial R}}\left[R^{2}{\frac {\partial D_{n}(R)}{\partial R}}\right]\,dR}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f6695154ee0e388c6ea1da20c2e19810282251a)
<math>\phi_n(\kappa) =
\frac{1}{4\pi^2\kappa^2} \int_0^\infty
\frac{\sin(\kappa R)}{\kappa R}
\frac{\partial}{\partial R}
\left[R^2\frac{\partial D_n(R)}{\partial R}\right]\,dR</math>
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ

<math>\phi_n(\kappa) =
0.033C_n^2\kappa^{-11/3},\quad
\frac{1}{L_0}\ll\kappa\ll\frac{1}{l_0}</math>
Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«џЯ»ЇЯ«џЯ«┐Я«»Я»ЂЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ«ЋЯ«│Я»ЂЯ««Я»Ї

<math>
f(x) =
\begin{cases}
1 & -1 \le x < 0 \\
\frac{1}{2} & x = 0 \\
1 - x^2 & \text{otherwise}
\end{cases}
</math>
Я««Я»ЂЯ«ЕЯ»ЇЯ«ЕЯ»іЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ Я«ЄЯ«ЪЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«ЋЯ»ђЯ«┤Я»іЯ«ЪЯ»ЇЯ«ЪЯ»Ђ

<math>{}_pF_q(a_1,\dots,a_p;c_1,\dots,c_q;z)
= \sum_{n=0}^\infty
\frac{(a_1)_n\cdots(a_p)_n}{(c_1)_n\cdots(c_q)_n}
\frac{z^n}{n!}</math>
Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ««Я»ЂЯ««Я»Ї Я«џЯ«┐Я«▒Я»ЂЯ«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ««Я»ЂЯ««Я»Ї
 <math>\frac{a}{b}\ \tfrac{a}{b}</math>
<math>\frac{a}{b}\ \tfrac{a}{b}</math>
Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ«│Я«хЯ»Ђ
 <math>S=dD\,\sin\alpha\!</math>
<math>S=dD\,\sin\alpha\!</math>
Volume of a sphere-stand
![{\displaystyle V={\frac {1}{6}}\pi h\left[3\left(r_{1}^{2}+r_{2}^{2}\right)+h^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/480eb74247c5f48886e4558d4eb5dd09e6649745) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒
<math>V=\frac16\pi h\left[3\left(r_1^2+r_2^2\right)+h^2\right]</math> Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒
<math>V=\frac16\pi h\left[3\left(r_1^2+r_2^2\right)+h^2\right]</math>
Я«фЯ«▓Я»ЇЯ«▓Я«┐Я«ЕЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї
 Я«јЯ«ЕЯ»ЇЯ«фЯ«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒
<math>\begin{align}
u & = \tfrac{1}{\sqrt{2}}(x+y) \qquad & x &= \tfrac{1}{\sqrt{2}}(u+v) \\
v & = \tfrac{1}{\sqrt{2}}(x-y) \qquad & y &= \tfrac{1}{\sqrt{2}}(u-v)
\end{align}</math> Я«јЯ«ЕЯ»ЇЯ«фЯ«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒
<math>\begin{align}
u & = \tfrac{1}{\sqrt{2}}(x+y) \qquad & x &= \tfrac{1}{\sqrt{2}}(u+v) \\
v & = \tfrac{1}{\sqrt{2}}(x-y) \qquad & y &= \tfrac{1}{\sqrt{2}}(u-v)
\end{align}</math>
Я«хЯ»ЄЯ«цЯ«┐Я«»Я«┐Я«»Я«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї
- Я««Я»ѓЯ«▓Я«ЋЯ»ЇЯ«ЋЯ»ѓЯ«▒Я»ЇЯ«▒Я»ЂЯ«џЯ»Ї Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЅЯ«│Я»ЇЯ«│Я»ђЯ«ЪЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«»Я»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ Я«ЁЯ«цЯ«▒Я»ЇЯ«ЋЯ»ЂЯ«░Я«┐Я«» Я«хЯ«ЋЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я»ђЯ«ЪЯ»ЂЯ«хЯ«цЯ»Ђ Я«ЁЯ«хЯ«џЯ«┐Я«»Я««Я»Ї. Я«ј.Я«ЋЯ«Й:
:CH3CH3 Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒
CH<sub>3</sub>CH<sub>3</sub> Я«јЯ«Е Я«ЅЯ«│Я»ЇЯ«│Я»ђЯ«ЪЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«» Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї.
- Я«џЯ»ЄЯ«░Я»ЇЯ«хЯ»ѕЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ѓЯ«▓Я«ЋЯ»ЇЯ«ЋЯ»ѓЯ«▒Я»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«џЯ»Ї Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«фЯ«Ъ Я«ЅЯ«│Я»ЇЯ«│Я«┐Я«ЪЯ«▓Я»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«џЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«ј.Я«ЋЯ«Й:
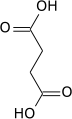
Я«фЯ»ЂЯ«»Я»ѓЯ««Я«░Я»ЄЯ«ЪЯ»ЇЯ«ЪЯ»Ђ

Я«џЯ«ЋЯ»ЇЯ«џЯ«┐Я«ЕЯ»ЄЯ«ЪЯ»ЇЯ«ЪЯ»Ђ
|












![{\displaystyle \surd ,{\sqrt {2}},{\sqrt[{n}]{}},{\sqrt[{3}]{x^{3}+y^{3} \over 2}}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9d0eb602bb67c297148e7454c160c7750cf84d7)


































![{\displaystyle A{\xleftarrow {n+\mu -1}}B{\xrightarrow[{T}]{n\pm i-1}}C}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0645e6df7ace8a40eba2d92f293f5fbd6f929411)




























































![{\displaystyle \phi _{n}(\kappa )={\frac {1}{4\pi ^{2}\kappa ^{2}}}\int _{0}^{\infty }{\frac {\sin(\kappa R)}{\kappa R}}{\frac {\partial }{\partial R}}\left[R^{2}{\frac {\partial D_{n}(R)}{\partial R}}\right]\,dR}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f6695154ee0e388c6ea1da20c2e19810282251a)





![{\displaystyle V={\frac {1}{6}}\pi h\left[3\left(r_{1}^{2}+r_{2}^{2}\right)+h^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/480eb74247c5f48886e4558d4eb5dd09e6649745)
















