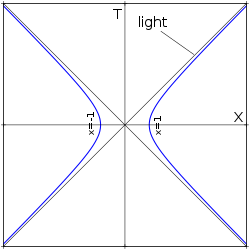
–ď—Ė–Ņ–Ķ—Ä–Ī–ĺ–Ľ—Ė—á–Ĺ–ł–Ļ —Ä—É—Ö –ľ–ĺ–∂–Ĺ–į –≤—Ė–ī–ĺ–Ī—Ä–į–∑–ł—ā–ł –Ĺ–į –ī—Ė–į–≥—Ä–į–ľ—Ė –ú—Ė–Ĺ–ļ–ĺ–≤—Ā—Ć–ļ–ĺ–≥–ĺ, –ī–Ķ —Ä—É—Ö –Ņ—Ä–ł—Ā–ļ–ĺ—Ä—é–≤–į–Ĺ–ĺ—ó —á–į—Ā—ā–ł–Ĺ–ļ–ł –≤—Ė–ī–Ī—É–≤–į—Ē—ā—Ć—Ā—Ź –≤–∑–ī–ĺ–≤–∂ –ĺ—Ā—Ė
X
{\displaystyle X}
x
=
¬Ī
c
2
/
őĪ
{\displaystyle x=\pm c^{2}/\alpha }
ő∑
=
őĪ
ŌĄ
/
c
{\displaystyle \eta =\alpha \tau /c}
c
=
1
,
őĪ
=
1
{\displaystyle c=1,\alpha =1}
2 –ď—Ė–Ņ–Ķ—Ä–Ī–ĺ–Ľ—Ė—á–Ĺ–ł–Ļ —Ä—É—Ö ‚ÄĒ —Ü–Ķ —Ä—É—Ö –ĺ–Ī'—Ē–ļ—ā–į –∑ –Ņ–ĺ—Ā—ā—Ė–Ļ–Ĺ–ł–ľ –í–Ľ–į—Ā–Ĺ–Ķ –Ņ—Ä–ł—Ā–ļ–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź –≤ —Ā–Ņ–Ķ—Ü—Ė–į–Ľ—Ć–Ĺ—Ė–Ļ —ā–Ķ–ĺ—Ä—Ė—ó –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ—Ā—ā—Ė . –ô–ĺ–≥–ĺ –Ĺ–į–∑–ł–≤–į—é—ā—Ć –≥—Ė–Ņ–Ķ—Ä–Ī–ĺ–Ľ—Ė—á–Ĺ–ł–ľ —Ä—É—Ö–ĺ–ľ, —ā–ĺ–ľ—É —Č–ĺ —Ä—Ė–≤–Ĺ—Ź–Ĺ–Ĺ—Ź, —Č–ĺ –ĺ–Ņ–ł—Ā—É—Ē —ā—Ä–į—Ē–ļ—ā–ĺ—Ä—Ė—é –ĺ–Ī'—Ē–ļ—ā–į –≤ –Ņ—Ä–ĺ—Ā—ā–ĺ—Ä—Ė-—á–į—Ā—Ė , —Ē –≥—Ė–Ņ–Ķ—Ä–Ī–ĺ–Ľ–ĺ—é , —Ź–ļ —Ü–Ķ –ľ–ĺ–∂–Ĺ–į –Ņ–ĺ–Ī–į—á–ł—ā–ł, —Ź–ļ—Č–ĺ –Ņ–ĺ–Ī—É–ī—É–≤–į—ā–ł –≥—Ä–į—Ą—Ė–ļ –Ĺ–į –ī—Ė–į–≥—Ä–į–ľ—Ė –ú—Ė–Ĺ–ļ–ĺ–≤—Ā—Ć–ļ–ĺ–≥–ĺ , –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł —Ź–ļ–ĺ—ó –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź—é—ā—Ć –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–Ĺ—É —Ė–Ĺ–Ķ—Ä—Ü—Ė–į–Ľ—Ć–Ĺ—É (–Ĺ–Ķ–Ņ—Ä–ł—Ā–ļ–ĺ—Ä–Ķ–Ĺ—É) —Ā–ł—Ā—ā–Ķ–ľ—É. –¶–Ķ–Ļ —Ä—É—Ö –ľ–į—Ē –ļ—Ė–Ľ—Ć–ļ–į —Ü—Ė–ļ–į–≤–ł—Ö –ĺ—Ā–ĺ–Ī–Ľ–ł–≤–ĺ—Ā—ā–Ķ–Ļ, –∑–ĺ–ļ—Ä–Ķ–ľ–į, —ā–ĺ–Ļ —Ą–į–ļ—ā, —Č–ĺ —Ą–ĺ—ā–ĺ–Ĺ –ľ–ĺ–∂–Ĺ–į –≤–ł–Ņ–Ķ—Ä–Ķ–ī–ł—ā–ł, —Ź–ļ—Č–ĺ –ľ–į—ā–ł –ī–ĺ—Ā—ā–į—ā–Ĺ—é –Ņ–Ķ—Ä–Ķ–≤–į–≥—É –Ĺ–į —Ā—ā–į—Ä—ā—Ė, —Ź–ļ —Ü–Ķ –ľ–ĺ–∂–Ĺ–į –Ņ–ĺ–Ī–į—á–ł—ā–ł –Ĺ–į –ī—Ė–į–≥—Ä–į–ľ–ł[ 1]
–ď–Ķ—Ä–ľ–į–Ĺ –ú—Ė–Ĺ–ļ–ĺ–≤—Ā—Ć–ļ–ł–Ļ (1908) –Ņ–ĺ–ļ–į–∑–į–≤ –∑–≤'—Ź–∑–ĺ–ļ –ľ—Ė–∂ —ā–ĺ—á–ļ–ĺ—é –Ĺ–į —Ā–≤—Ė—ā–ĺ–≤—Ė–Ļ –Ľ—Ė–Ĺ—Ė—ó —ā–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ—é 4-–Ņ—Ä–ł—Ā–ļ–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź —ā–į ¬ę–≥—Ė–Ņ–Ķ—Ä–Ī–ĺ–Ľ–ł –≤–ł–ļ—Ä–ł–≤–Ľ–Ķ–Ĺ–Ĺ—Ź¬Ľ (–Ĺ—Ė–ľ. Kr√ľmmungshyperbel )[ 2] –∂–ĺ—Ä—Ā—ā–ļ–ĺ—Ā—ā—Ė –Ď–ĺ—Ä–Ĺ–į [en] –ú–į–ļ—Ā –Ď–ĺ—Ä–Ĺ (1909) –∑–≥–ĺ–ī–ĺ–ľ –≤–≤—Ė–≤ —ā–Ķ—Ä–ľ—Ė–Ĺ ¬ę–≥—Ė–Ņ–Ķ—Ä–Ī–ĺ–Ľ—Ė—á–Ĺ–ł–Ļ —Ä—É—Ö¬Ľ (–Ĺ—Ė–ľ. Hyperbelbewegung ) –ī–Ľ—Ź –≤–ł–Ņ–į–ī–ļ—É –Ņ–ĺ—Ā—ā—Ė–Ļ–Ĺ–ĺ—ó –≤–Ķ–Ľ–ł—á–ł–Ĺ–ł 4-–Ņ—Ä–ł—Ā–ļ–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź, —Ė –Ņ–ĺ—ā—Ė–ľ –Ĺ–į–ī–į–≤ –ī–Ķ—ā–į–Ľ—Ć–Ĺ–ł–Ļ –ĺ–Ņ–ł—Ā –∑–į—Ä—Ź–ī–∂–Ķ–Ĺ–ł—Ö —á–į—Ā—ā–ł–Ĺ–ĺ–ļ —É –≥—Ė–Ņ–Ķ—Ä–Ī–ĺ–Ľ—Ė—á–Ĺ–ĺ–ľ—É —Ä—É—Ā—Ė —ā–į –≤–≤—Ė–≤ –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–Ĺ—É ¬ę–≥—Ė–Ņ–Ķ—Ä–Ī–ĺ–Ľ—Ė—á–Ĺ–ĺ –Ņ—Ä–ł—Ā–ļ–ĺ—Ä–Ķ–Ĺ—É —Ā–ł—Ā—ā–Ķ–ľ—É –≤—Ė–ī–Ľ—Ė–ļ—ɬĽ (–Ĺ—Ė–ľ. hyperbolisch beschleunigtes Bezugsystem )[ 3] –ź—Ä–Ĺ–ĺ–Ľ—Ć–ī–ĺ–ľ –ó–ĺ–ľ–ľ–Ķ—Ä—Ą–Ķ–Ľ—Ć–ī–ĺ–ľ (1910)[ 4] –ú–į–ļ—Ā–į —Ą–ĺ–Ĺ –õ–į—É–Ķ (1911, 1921)[ 5] –í–ĺ–Ľ—Ć—Ą–≥–į–Ĺ–≥–į –ü–į—É–Ľ—Ė (1921)[ 6] [ 7] [ 8] –ü—Ä–ł—Ā–ļ–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź (—Ā–Ņ–Ķ—Ü—Ė–į–Ľ—Ć–Ĺ–į —ā–Ķ–ĺ—Ä—Ė—Ź –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ—Ā—ā—Ė) [en]
–í–Ľ–į—Ā–Ĺ–Ķ –Ņ—Ä–ł—Ā–ļ–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź
őĪ
{\displaystyle \alpha }
–Ņ—Ä–ł—Ā–ļ–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź , —Ź–ļ–Ķ ¬ę–≤—Ė–ī—á—É–≤–į—Ē¬Ľ —á–į—Ā—ā–ł–Ĺ–ļ–į, –ļ–ĺ–Ľ–ł –≤–ĺ–Ĺ–į –Ņ—Ä–ł—Ā–ļ–ĺ—Ä—é—Ē—ā—Ć—Ā—Ź –≤—Ė–ī –ĺ–ī–Ĺ—Ė—Ē—ó —Ė–Ĺ–Ķ—Ä—Ü—Ė–į–Ľ—Ć–Ĺ–ĺ—ó —Ā–ł—Ā—ā–Ķ–ľ–ł –≤—Ė–ī–Ľ—Ė–ļ—É –ī–ĺ —Ė–Ĺ—ą–ĺ—ó. –Į–ļ—Č–ĺ –≤–Ľ–į—Ā–Ĺ–Ķ –Ņ—Ä–ł—Ā–ļ–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź —Ā–Ņ—Ä—Ź–ľ–ĺ–≤–į–Ĺ–Ķ –Ņ–į—Ä–į–Ľ–Ķ–Ľ—Ć–Ĺ–ĺ –Ľ—Ė–Ĺ—Ė—ó —Ä—É—Ö—É, –≤–ĺ–Ĺ–ĺ –Ņ–ĺ–≤'—Ź–∑–į–Ĺ–Ķ –∑—Ė –∑–≤–ł—á–į–Ļ–Ĺ–ł–ľ 3-–Ņ—Ä–ł—Ā–ļ–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź–ľ —Ā–Ņ–Ķ—Ü—Ė–į–Ľ—Ć–Ĺ–ĺ—ó —ā–Ķ–ĺ—Ä—Ė—ó –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ—Ā—ā—Ė [en]
a
=
d
u
/
d
T
{\displaystyle a=du/dT}
őĪ
=
ő≥
3
a
=
1
(
1
‚ąí
u
2
/
c
2
)
3
/
2
d
u
d
T
,
{\displaystyle \alpha =\gamma ^{3}a={\frac {1}{\left(1-u^{2}/c^{2}\right)^{3/2}}}{\frac {du}{dT}},}
–ī–Ķ
u
{\displaystyle u}
‚ÄĒ –ľ–ł—ā—ā—Ē–≤–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć —á–į—Ā—ā–ł–Ĺ–ļ–ł,
ő≥
{\displaystyle \gamma }
‚ÄĒ —Ą–į–ļ—ā–ĺ—Ä –õ–ĺ—Ä–Ķ–Ĺ—Ü–į ,
c
{\displaystyle c}
‚ÄĒ —Ü–Ķ —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć —Ā–≤—Ė—ā–Ľ–į , –į
T
{\displaystyle T}
‚ÄĒ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ–ł–Ļ —á–į—Ā. –†–ĺ–∑–≤'—Ź–∑–į–Ĺ–Ĺ—Ź —Ä—Ė–≤–Ĺ—Ź–Ĺ–Ĺ—Ź —Ä—É—Ö—É –ī–į—Ē —ą—É–ļ–į–Ĺ—Ė —Ą–ĺ—Ä–ľ—É–Ľ–ł, —Ź–ļ—Ė –ľ–ĺ–∂–Ĺ–į –≤–ł—Ä–į–∑–ł—ā–ł —á–Ķ—Ä–Ķ–∑ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ–ł–Ļ —á–į—Ā
T
{\displaystyle T}
–≤–Ľ–į—Ā–Ĺ–ł–Ļ —á–į—Ā
ŌĄ
{\displaystyle \tau }
[ 5] [ 6] [ 9] [ 10] [ 11]
u
(
T
)
=
őĪ
T
1
+
(
őĪ
T
c
)
2
=
c
tanh
‚Ā°
(
arsinh
‚Ā°
őĪ
T
c
)
X
(
T
)
=
c
2
őĪ
(
1
+
(
őĪ
T
c
)
2
‚ąí
1
)
=
c
2
őĪ
(
cosh
‚Ā°
(
arsinh
‚Ā°
őĪ
T
c
)
‚ąí
1
)
c
ŌĄ
(
T
)
=
c
2
őĪ
ln
‚Ā°
(
1
+
(
őĪ
T
c
)
2
+
őĪ
T
c
)
=
c
2
őĪ
arsinh
‚Ā°
őĪ
T
c
u
(
ŌĄ
)
=
c
tanh
‚Ā°
őĪ
ŌĄ
c
X
(
ŌĄ
)
=
c
2
őĪ
(
cosh
‚Ā°
őĪ
ŌĄ
c
‚ąí
1
)
c
T
(
ŌĄ
)
=
c
2
őĪ
sinh
‚Ā°
őĪ
ŌĄ
c
{\displaystyle {\begin{array}{c|c}{\begin{aligned}u(T)&={\frac {\alpha T}{\sqrt {1+\left({\frac {\alpha T}{c}}\right)^{2}}}}\\&=c\tanh \left(\operatorname {arsinh} {\frac {\alpha T}{c}}\right)\\X(T)&={\frac {c^{2}}{\alpha }}\left({\sqrt {1+\left({\frac {\alpha T}{c}}\right)^{2}}}-1\right)\\&={\frac {c^{2}}{\alpha }}\left(\cosh \left(\operatorname {arsinh} {\frac {\alpha T}{c}}\right)-1\right)\\c\tau (T)&={\frac {c^{2}}{\alpha }}\ln \left({\sqrt {1+\left({\frac {\alpha T}{c}}\right)^{2}}}+{\frac {\alpha T}{c}}\right)\\&={\frac {c^{2}}{\alpha }}\operatorname {arsinh} {\frac {\alpha T}{c}}\end{aligned}}&{\begin{aligned}u(\tau )&=c\tanh {\frac {\alpha \tau }{c}}\\\\X(\tau )&={\frac {c^{2}}{\alpha }}\left(\cosh {\frac {\alpha \tau }{c}}-1\right)\\\\cT(\tau )&={\frac {c^{2}}{\alpha }}\sinh {\frac {\alpha \tau }{c}}\\\\\\\end{aligned}}\end{array}}}
(1
–¶–Ķ –Ņ—Ä–ł–∑–≤–ĺ–ī–ł—ā—Ć –ī–ĺ —Ä—Ė–≤–Ĺ—Ź–Ĺ–Ĺ—Ź
(
X
+
c
2
/
őĪ
)
2
‚ąí
c
2
T
2
=
c
4
/
őĪ
2
{\displaystyle \left(X+c^{2}/\alpha \right)^{2}-c^{2}T^{2}=c^{4}/\alpha ^{2}}
X
{\displaystyle X}
X
=
0
{\displaystyle X=0}
T
=
0
{\displaystyle T=0}
[ 12] [ 13] [ 14]
u
(
T
)
=
u
0
ő≥
0
+
őĪ
T
1
+
(
u
0
ő≥
0
+
őĪ
T
c
)
2
=
c
tanh
‚Ā°
{
arsinh
‚Ā°
(
u
0
ő≥
0
+
őĪ
T
c
)
}
X
(
T
)
=
X
0
+
c
2
őĪ
(
1
+
(
u
0
ő≥
0
+
őĪ
T
c
)
2
‚ąí
ő≥
0
)
=
X
0
+
c
2
őĪ
{
cosh
‚Ā°
[
arsinh
‚Ā°
(
u
0
ő≥
0
+
őĪ
T
c
)
]
‚ąí
ő≥
0
}
c
ŌĄ
(
T
)
=
c
ŌĄ
0
+
c
2
őĪ
ln
‚Ā°
(
c
2
+
(
u
0
ő≥
0
+
őĪ
T
)
2
+
u
0
ő≥
0
+
őĪ
T
(
c
+
u
0
)
ő≥
0
)
=
c
ŌĄ
0
+
c
2
őĪ
{
arsinh
‚Ā°
(
u
0
ő≥
0
+
őĪ
T
c
)
‚ąí
artanh
‚Ā°
(
u
0
c
)
}
u
(
ŌĄ
)
=
c
tanh
‚Ā°
{
artanh
‚Ā°
(
u
0
c
)
+
őĪ
ŌĄ
c
}
X
(
ŌĄ
)
=
X
0
+
c
2
őĪ
{
cosh
‚Ā°
[
artanh
‚Ā°
(
u
0
c
)
+
őĪ
ŌĄ
c
]
‚ąí
ő≥
0
}
c
T
(
ŌĄ
)
=
c
T
0
+
c
2
őĪ
{
sinh
‚Ā°
[
artanh
‚Ā°
(
u
0
c
)
+
őĪ
ŌĄ
c
]
‚ąí
u
0
ő≥
0
c
}
{\displaystyle {\scriptstyle {\begin{array}{c|c}{\begin{aligned}u(T)&={\frac {u_{0}\gamma _{0}+\alpha T}{\sqrt {1+\left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)^{2}}}}\quad \\&=c\tanh \left\{\operatorname {arsinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)\right\}\\X(T)&=X_{0}+{\frac {c^{2}}{\alpha }}\left({\sqrt {1+\left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)^{2}}}-\gamma _{0}\right)\\&=X_{0}+{\frac {c^{2}}{\alpha }}\left\{\cosh \left[\operatorname {arsinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)\right]-\gamma _{0}\right\}\\c\tau (T)&=c\tau _{0}+{\frac {c^{2}}{\alpha }}\ln \left({\frac {{\sqrt {c^{2}+\left(u_{0}\gamma _{0}+\alpha T\right){}^{2}}}+u_{0}\gamma _{0}+\alpha T}{\left(c+u_{0}\right)\gamma _{0}}}\right)\\&=c\tau _{0}+{\frac {c^{2}}{\alpha }}\left\{\operatorname {arsinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)-\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)\right\}\end{aligned}}&{\begin{aligned}u(\tau )&=c\tanh \left\{\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right\}\\\\X(\tau )&=X_{0}+{\frac {c^{2}}{\alpha }}\left\{\cosh \left[\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right]-\gamma _{0}\right\}\\\\cT(\tau )&=cT_{0}+{\frac {c^{2}}{\alpha }}\left\{\sinh \left[\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right]-{\frac {u_{0}\gamma _{0}}{c}}\right\}\end{aligned}}\end{array}}}}
–°–≤—Ė—ā–ĺ–≤—É –Ľ—Ė–Ĺ—Ė—é –ī–Ľ—Ź –≥—Ė–Ņ–Ķ—Ä–Ī–ĺ–Ľ—Ė—á–Ĺ–ĺ–≥–ĺ —Ä—É—Ö—É (—Ź–ļ—É –≤—Ė–ī—ā–Ķ–Ņ–Ķ—Ä –Ī—É–ī–Ķ–ľ–ĺ –∑–į–Ņ–ł—Ā—É–≤–į—ā–ł —Ź–ļ —Ą—É–Ĺ–ļ—Ü—Ė—é –≤–Ľ–į—Ā–Ĺ–ĺ–≥–ĺ —á–į—Ā—É) –ľ–ĺ–∂–Ĺ–į —Ā–Ņ—Ä–ĺ—Ā—ā–ł—ā–ł –ļ—Ė–Ľ—Ć–ļ–ĺ–ľ–į —Ā–Ņ–ĺ—Ā–ĺ–Ī–į–ľ–ł. –Ě–į–Ņ—Ä–ł–ļ–Ľ–į–ī, –≤–ł—Ä–į–∑
X
=
c
2
őĪ
(
cosh
‚Ā°
őĪ
ŌĄ
c
‚ąí
1
)
{\displaystyle X={\frac {c^{2}}{\alpha }}\left(\cosh {\frac {\alpha \tau }{c}}-1\right)}
–ľ–ĺ–∂–Ķ –Ī—É—ā–ł –Ņ—Ė–ī–ī–į–Ĺ–ĺ –Ņ—Ä–ĺ—Ā—ā–ĺ—Ä–ĺ–≤–ĺ–ľ—É –∑—Ā—É–≤—É –Ĺ–į
c
2
/
őĪ
{\displaystyle c^{2}/\alpha }
X
=
c
2
őĪ
cosh
‚Ā°
őĪ
ŌĄ
c
{\displaystyle X={\frac {c^{2}}{\alpha }}\cosh {\frac {\alpha \tau }{c}}}
[ 15]
—É –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–Ĺ–ĺ—Ā—ā—Ė –ī–ĺ —á–ĺ–≥–ĺ —Ā–Ņ–ĺ—Ā—ā–Ķ—Ä—Ė–≥–į—á –∑–Ĺ–į—Ö–ĺ–ī–ł—ā—Ć—Ā—Ź –≤ —ā–ĺ—á—Ü—Ė
X
=
c
2
/
őĪ
{\displaystyle X=c^{2}/\alpha }
T
=
0
{\displaystyle T=0}
x
=
c
2
/
őĪ
{\displaystyle x=c^{2}/\alpha }
—Ā—ā—Ä—Ė–ľ–ļ—Ė—Ā—ā—Ć
ő∑
=
artanh
‚Ā°
u
c
=
őĪ
ŌĄ
c
{\displaystyle \eta =\operatorname {artanh} {\frac {u}{c}}={\frac {\alpha \tau }{c}}}
[ 14] [ 4] [ 16]
c
T
=
x
sinh
‚Ā°
ő∑
,
X
=
x
cosh
‚Ā°
ő∑
{\displaystyle cT=x\sinh \eta ,\quad X=x\cosh \eta }
(2
–∑ –≥—Ė–Ņ–Ķ—Ä–Ī–ĺ–Ľ–ĺ—é
X
2
‚ąí
c
2
T
2
=
x
2
{\displaystyle X^{2}-c^{2}T^{2}=x^{2}}
–Ď–ĺ—Ä–Ĺ (1909)[ 3] [ 4] [ 5] [ 6] –Ķ–Ľ–Ķ–ļ—ā—Ä–ĺ–ľ–į–≥–Ĺ—Ė—ā–Ĺ–ĺ–≥–ĺ –Ņ–ĺ–Ľ—Ź –∑–į—Ä—Ź–ī–∂–Ķ–Ĺ–ł—Ö —á–į—Ā—ā–ł–Ĺ–ĺ–ļ —É –≥—Ė–Ņ–Ķ—Ä–Ī–ĺ–Ľ—Ė—á–Ĺ–ĺ–ľ—É —Ä—É—Ā—Ė[ 7] –ď–Ķ—Ä–ľ–į–Ĺ–ĺ–ľ –Ď–ĺ–Ĺ–ī—Ė —Ė –Ę–ĺ–ľ–į—Ā–ĺ–ľ –ď–ĺ–Ľ–ī–ĺ–ľ (1955)[ 17] [ 18] [ 19]
E
ŌĀ
′
′
=
(
8
e
/
őĪ
2
)
ŌĀ
′
z
′
őĺ
′
3
E
z
′
′
=
‚ąí
(
4
e
/
őĪ
2
)
1
/
őĪ
2
+
t
′
2
+
ŌĀ
′
2
‚ąí
z
′
2
őĺ
′
3
E
ŌÜ
′
′
=
H
ŌÜ
′
′
=
H
z
′
′
=
0
H
ŌÜ
′
′
=
(
8
e
/
őĪ
2
)
ŌĀ
′
t
′
őĺ
′
3
őĺ
′
=
(
1
/
őĪ
2
+
t
′
2
‚ąí
ŌĀ
′
2
‚ąí
z
′
2
)
2
+
(
2
ŌĀ
′
/
őĪ
)
2
{\displaystyle {\begin{aligned}E_{\rho '}'=&{\frac {\left(8e/\alpha ^{2}\right)\rho 'z'}{\xi ^{\prime 3}}}\\E_{z'}'=&{\frac {-\left(4e/\alpha ^{2}\right)1/\alpha ^{2}+t^{\prime 2}+\rho ^{\prime 2}-z^{\prime 2}}{\xi ^{\prime 3}}}\\E_{\varphi '}'=&H_{\varphi '}'=H_{z'}'=0\\H_{\varphi '}'=&{\frac {\left(8e/\alpha ^{2}\right)\rho 't'}{\xi ^{\prime 3}}}\\\xi '=&{\sqrt {\left(1/\alpha ^{2}+t^{\prime 2}-\rho ^{\prime 2}-z^{\prime 2}\right)^{2}+\left(2\rho '/\alpha \right)^{2}}}\end{aligned}}}
–¶–Ķ –Ņ–ĺ–≤'—Ź–∑–į–Ĺ–ĺ –∑ —Ā—É–Ņ–Ķ—Ä–Ķ—á–Ľ–ł–≤–ł–ľ[ 20] [ 21] –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–ĺ–ľ –Ķ–ļ–≤—Ė–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ–ĺ—Ā—ā—Ė ‚ÄĒ –Ĺ–į–≤—Ė—ā—Ć —Ź–ļ—Č–ĺ –ľ–ĺ–≤–į –Ļ–ī–Ķ –Ņ—Ä–ĺ —Ė–ī–Ķ–į–Ľ—Ć–Ĺ—É —Ā–ł—ā—É–į—Ü—Ė—é, –ĺ—Ā–ļ—Ė–Ľ—Ć–ļ–ł –≤—Ė—á–Ĺ–ł–Ļ –≥—Ė–Ņ–Ķ—Ä–Ī–ĺ–Ľ—Ė—á–Ĺ–ł–Ļ —Ä—É—Ö –Ĺ–Ķ–ľ–ĺ–∂–Ľ–ł–≤–ł–Ļ. –£ —ā–ĺ–Ļ —á–į—Ā —Ź–ļ —Ä–į–Ĺ–Ĺ—Ė –į–≤—ā–ĺ—Ä–ł, —ā–į–ļ—Ė —Ź–ļ –Ď–ĺ—Ä–Ĺ (1909) –į–Ī–ĺ –ü–į—É–Ľ—Ė (1921), —Ā—ā–≤–Ķ—Ä–ī–∂—É–≤–į–Ľ–ł, —Č–ĺ –≤–ł–Ņ—Ä–ĺ–ľ—Ė–Ĺ—é–≤–į–Ĺ–Ĺ—Ź –Ĺ–Ķ –≤–ł–Ĺ–ł–ļ–į—Ē, –Ņ—Ė–∑–Ĺ—Ė—ą—Ė –į–≤—ā–ĺ—Ä–ł, —ā–į–ļ—Ė —Ź–ļ –Ď–ĺ–Ĺ–ī—Ė —Ė –ď–ĺ–Ľ–ī[ 17] [ 18] [ 19]
–®–Ľ—Ź—Ö —Ā–≤—Ė—ā–Ľ–į —á–Ķ—Ä–Ķ–∑ E –Ņ–ĺ–∑–Ĺ–į—á–į—Ē –≤–ł–ī–ł–ľ–ł–Ļ –≥–ĺ—Ä–ł–∑–ĺ–Ĺ—ā –Ņ–ĺ–ī—Ė–Ļ —Ā–Ņ–ĺ—Ā—ā–Ķ—Ä—Ė–≥–į—á–į P —É –≥—Ė–Ņ–Ķ—Ä–Ī–ĺ–Ľ—Ė—á–Ĺ–ĺ–ľ—É —Ä—É—Ā—Ė. –£ —Ä—Ė–≤–Ĺ—Ź–Ĺ–Ĺ—Ė (2
x
{\displaystyle x}
ő∑
{\displaystyle \eta }
[ 16]
x
{\displaystyle x}
ő∑
{\displaystyle \eta }
(
x
,
y
,
z
,
ő∑
)
{\displaystyle (x,y,z,\eta )}
c
T
=
x
sinh
‚Ā°
ő∑
,
X
=
x
cosh
‚Ā°
ő∑
,
Y
=
y
,
Z
=
z
{\displaystyle cT=x\sinh \eta ,\quad X=x\cosh \eta ,\quad Y=y,\quad Z=z}
–ó–į –ī–ĺ–Ņ–ĺ–ľ–ĺ–≥–ĺ—é —Ü—Ć–ĺ–≥–ĺ –Ņ–Ķ—Ä–Ķ—ā–≤–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź –≤–Ľ–į—Ā–Ĺ–ł–Ļ —á–į—Ā —Ā—ā–į—Ē —á–į—Ā–ĺ–ľ –≥—Ė–Ņ–Ķ—Ä–Ī–ĺ–Ľ—Ė—á–Ĺ–ĺ –Ņ—Ä–ł—Ā–ļ–ĺ—Ä–Ķ–Ĺ–ĺ—ó —Ā–ł—Ā—ā–Ķ–ľ–ł. –¶—Ė –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł, —Ź–ļ—Ė –∑–į–∑–≤–ł—á–į–Ļ –Ĺ–į–∑–ł–≤–į—é—ā—Ć –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į–ľ–ł –†—Ė–Ĺ–ī–Ľ–Ķ—Ä–į (–Ņ–ĺ–ī—Ė–Ī–Ĺ—Ė –≤–į—Ä—Ė–į–Ĺ—ā–ł –Ĺ–į–∑–ł–≤–į—é—ā—Ć—Ā—Ź –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į–ľ–ł –ö–ĺ—ā—ā–Ľ–Ķ—Ä–į-–ú–Ķ–Ľ–Ľ–Ķ—Ä–į –į–Ī–ĺ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į–ľ–ł –õ–į—Ā—Ā–į [en] –Ķ—Ą–Ķ–ļ—ā–ĺ–ľ –£–Ĺ—Ä—É . –ü—Ä–ł —Ä–ĺ–∑–≥–Ľ—Ź–ī—Ė —Ü–ł—Ö –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –≤–ł—Ź–≤–Ľ—Ź—Ē—ā—Ć—Ā—Ź, —Č–ĺ —Ā–Ņ–ĺ—Ā—ā–Ķ—Ä—Ė–≥–į—á—Ė –≤ –≥—Ė–Ņ–Ķ—Ä–Ī–ĺ–Ľ—Ė—á–Ĺ–ĺ–ľ—É —Ä—É—Ā—Ė –ľ–į—é—ā—Ć –≤–ł–ī–ł–ľ–ł–Ļ –≥–ĺ—Ä–ł–∑–ĺ–Ĺ—ā –Ņ–ĺ–ī—Ė–Ļ , –∑-–∑–į –ľ–Ķ–∂ —Ź–ļ–ĺ–≥–ĺ –ī–ĺ –Ĺ–ł—Ö –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī—Ė–Ļ—ā–ł –∂–ĺ–ī–Ķ–Ĺ —Ā–ł–≥–Ĺ–į–Ľ.
–ú–Ķ–Ĺ—ą –≤—Ė–ī–ĺ–ľ–ł–ľ –ľ–Ķ—ā–ĺ–ī–ĺ–ľ –≤–ł–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź —Ā–ł—Ā—ā–Ķ–ľ–ł –≤—Ė–ī–Ľ—Ė–ļ—É –≤ –≥—Ė–Ņ–Ķ—Ä–Ī–ĺ–Ľ—Ė—á–Ĺ–ĺ–ľ—É —Ä—É—Ā—Ė —Ē –≤–ł–ļ–ĺ—Ä–ł—Ā—ā–į–Ĺ–Ĺ—Ź —Ā–Ņ–Ķ—Ü—Ė–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ļ–ĺ–Ĺ—Ą–ĺ—Ä–ľ–Ĺ–ĺ–≥–ĺ –Ņ–Ķ—Ä–Ķ—ā–≤–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź [en] —Ė–Ĺ–≤–Ķ—Ä—Ā—Ė—ó [en] —ā—Ä–į–Ĺ—Ā–Ľ—Ź—Ü—Ė—ó —ā–į —Ė–Ĺ—ą–ĺ—ó —Ė–Ĺ–≤–Ķ—Ä—Ā—Ė—ó[ 22] –ļ–į–Ľ—Ė–Ī—Ä—É–≤–į–Ľ—Ć–Ĺ–Ķ –Ņ–Ķ—Ä–Ķ—ā–≤–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź –≤ –Ņ—Ä–ĺ—Ā—ā–ĺ—Ä—Ė –ú—Ė–Ĺ–ļ–ĺ–≤—Ā—Ć–ļ–ĺ–≥–ĺ, —Ö–ĺ—á–į –ī–Ķ—Ź–ļ—Ė –į–≤—ā–ĺ—Ä–ł –į–Ľ—Ć—ā–Ķ—Ä–Ĺ–į—ā–ł–≤–Ĺ–ĺ –≤–ł–ļ–ĺ—Ä–ł—Ā—ā–ĺ–≤—É—é—ā—Ć –Ļ–ĺ–≥–ĺ —Ź–ļ –Ņ–Ķ—Ä–Ķ—ā–≤–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź –Ņ—Ä–ł—Ā–ļ–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź (–ī–ł–≤. –ö–į—Ā—ā—Ä—É–Ņ –ī–Ľ—Ź –ļ—Ä–ł—ā–ł—á–Ĺ–ĺ–≥–ĺ —Ė—Ā—ā–ĺ—Ä–ł—á–Ĺ–ĺ–≥–ĺ –ĺ–≥–Ľ—Ź–ī—É)[ 23]
X
őľ
=
x
őľ
‚ąí
a
őľ
x
2
1
‚ąí
2
a
x
+
a
2
x
2
{\displaystyle X^{\mu }={\frac {x^{\mu }-a^{\mu }x^{2}}{1-2ax+a^{2}x^{2}}}}
–í–ł–ļ–ĺ—Ä–ł—Ā—ā–ĺ–≤—É—é—á–ł –Ľ–ł—ą–Ķ –ĺ–ī–ł–Ĺ –Ņ—Ä–ĺ—Ā—ā–ĺ—Ä–ĺ–≤–ł–Ļ –≤–ł–ľ—Ė—Ä
x
őľ
=
(
t
,
x
)
{\displaystyle x^{\mu }=(t,x)}
x
=
0
{\displaystyle x=0}
a
őľ
=
(
0
,
‚ąí
őĪ
/
2
)
{\displaystyle a^{\mu }=(0,-\alpha /2)}
[ 24]
T
=
t
1
‚ąí
1
4
őĪ
2
t
2
,
X
=
‚ąí
őĪ
t
2
2
(
1
‚ąí
1
4
őĪ
2
t
2
)
{\displaystyle T={\frac {t}{1-{\frac {1}{4}}\alpha {}^{2}t^{2}}},\quad X={\frac {-\alpha t^{2}}{2\left(1-{\frac {1}{4}}\alpha {}^{2}t^{2}\right)}}}
–∑ –≥—Ė–Ņ–Ķ—Ä–Ī–ĺ–Ľ–ĺ—é
(
X
‚ąí
1
/
őĪ
)
2
‚ąí
T
2
=
1
/
őĪ
2
{\displaystyle \left(X-1/\alpha \right)^{2}-T^{2}=1/\alpha ^{2}}
t
=
¬Ī
(
x
+
2
/
őĪ
)
{\displaystyle t=\pm (x+2/\alpha )}
[ 24] [ 23]
‚ÜĎ Misner, Thorne —ā–į Wheeler, 1973 , Chapter 6.‚ÜĎ Minkowski, Hermann (1909). Raum und Zeit. Vortrag, gehalten auf der 80. Naturforscher-Versammlung zu K√∂ln am 21. September 1908 [Wikisource translation: Space and Time ]. Jahresbericht der Deutschen Mathematiker-Vereinigung (–Ĺ—Ė–ľ.) . Leipzig. ‚ÜĎ –į –Ī Born, Max (1909). Die Theorie des starren Elektrons in der Kinematik des Relativit√§tsprinzips [–Ę–Ķ–ĺ—Ä—Ė—Ź –∂–ĺ—Ä—Ā—ā–ļ–ĺ–≥–ĺ –Ķ–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–į –≤ –ļ—Ė–Ĺ–Ķ–ľ–į—ā–ł—Ü—Ė –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ—É –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ—Ā—ā—Ė]. Annalen der Physik (–Ĺ—Ė–ľ.) . 335 (11): 1‚ÄĒ56. Bibcode :1909AnP...335....1B . doi :10.1002/andp.19093351102 . ‚ÜĎ –į –Ī –≤ Sommerfeld, Arnold (1910). Zur Relativit√§tstheorie II: Vierdimensionale Vektoranalysis [–ü—Ä–ĺ —ā–Ķ–ĺ—Ä—Ė—é –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ—Ā—ā—Ė II: –ß–ĺ—ā–ł—Ä–ł–≤–ł–ľ—Ė—Ä–Ĺ–ł–Ļ –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ł–Ļ –į–Ĺ–į–Ľ—Ė–∑]. Annalen der Physik (–Ĺ—Ė–ľ.) . 338 (14): 649‚ÄĒ689. Bibcode :1910AnP...338..649S . doi :10.1002/andp.19103381402 . ‚ÜĎ –į –Ī –≤ von Laue, M. (1921). Die Relativit√§tstheorie, Band 1 (–Ĺ—Ė–ľ.) (–≤–ł–ī. fourth edition of "Das Relativit√§tsprinzip"). Vieweg. —Ā. 89 ‚Äď90, 155‚ÄĒ166. ‚ÜĎ –į –Ī –≤ Pauli, Wolfgang (1921), Die Relativit√§tstheorie , Encyclop√§die der Mathematischen Wissenschaften (–Ĺ—Ė–ľ.) , 5 (2): 539‚ÄĒ776Pauli, W. (1981). Theory of Relativity (–į–Ĺ–≥–Ľ.) . –Ę. 165. Dover Publications. ISBN 0-486-64152-X ‚ÜĎ –į –Ī Galeriu, C. (2017). Electric charge in hyperbolic motion: the early history [–ē–Ľ–Ķ–ļ—ā—Ä–ł—á–Ĺ–ł–Ļ –∑–į—Ä—Ź–ī —É –≥—Ė–Ņ–Ķ—Ä–Ī–ĺ–Ľ—Ė—á–Ĺ–ĺ–ľ—É —Ä—É—Ā—Ė: —Ä–į–Ĺ–Ĺ—Ź —Ė—Ā—ā–ĺ—Ä—Ė—Ź]. Archive for History of Exact Sciences (–į–Ĺ–≥–Ľ.) . 71 (4): 1‚ÄĒ16. arXiv :1509.02504 doi :10.1007/s00407-017-0191-x . ‚ÜĎ Gourgoulhon, E. (2013). Special Relativity in General Frames: From Particles to Astrophysics (–į–Ĺ–≥–Ľ.) . Springer. —Ā. 396. ISBN 978-3642372766 ‚ÜĎ M√łller, C. (1955). The theory of relativity (–į–Ĺ–≥–Ľ.) . Oxford Clarendon Press. —Ā. 74 ‚Äď75. ‚ÜĎ Rindler, W. (1977). Essential Relativity (–į–Ĺ–≥–Ľ.) . Springer. —Ā. 49 ‚Äď50. ISBN 354007970X ‚ÜĎ PhysicsFAQ (2016), "Relativistic rocket", see external links
‚ÜĎ Gallant, J. (2012). Doing Physics with Scientific Notebook: A Problem Solving Approach (–į–Ĺ–≥–Ľ.) . John Wiley & Sons. —Ā. 437‚ÄĒ441. ISBN 978-0470665978 ‚ÜĎ M√ľller, T., King, A., & Adis, D. (2006). A trip to the end of the universe and the twin "paradox". American Journal of Physics (–į–Ĺ–≥–Ľ.) . 76 (4): 360‚ÄĒ373. arXiv :physics/0612126 Bibcode :2008AmJPh..76..360M . doi :10.1119/1.2830528 . ‚ÜĎ –į –Ī Fraundorf, P. (2012). A traveler-centered intro to kinematics (–į–Ĺ–≥–Ľ.) : IV‚ÄĒB. arXiv :1206.2877 Bibcode :2012arXiv1206.2877F . ‚ÜĎ Pauli (1921), p. 628, used the notation
x
4
=
a
ch
‚Ā°
c
t
a
{\displaystyle x^{4}=a\operatorname {ch} {\frac {ct}{a}}}
a
=
c
2
b
{\displaystyle a={\frac {c^{2}}{b}}}
‚ÜĎ –į –Ī Sommerfeld (1910), pp. 670-671 used the form
x
=
r
cos
‚Ā°
(
ŌÜ
)
{\displaystyle x=r\cos(\varphi )}
l
=
r
sin
‚Ā°
(
ŌÜ
)
{\displaystyle l=r\sin(\varphi )}
i
Ōą
{\displaystyle i\psi }
l
=
i
c
t
{\displaystyle l=ict}
‚ÜĎ –į –Ī Bondi, H., & Gold, T. (1955). The field of a uniformly accelerated charge, with special reference to the problem of gravitational acceleration. Proceedings of the Royal Society of London (–į–Ĺ–≥–Ľ.) . 229 (1178): 416‚ÄĒ424. Bibcode :1955RSPSA.229..416B . doi :10.1098/rspa.1955.0098 . ‚ÜĎ –į –Ī Fulton, Thomas; Rohrlich, Fritz (1960). Classical radiation from a uniformly accelerated charge. Annals of Physics (–į–Ĺ–≥–Ľ.) . 9 (4): 499‚ÄĒ517. Bibcode :1960AnPhy...9..499F . doi :10.1016/0003-4916(60)90105-6 . ‚ÜĎ –į –Ī Rohrlich, Fritz (1963). The principle of equivalence. Annals of Physics (–į–Ĺ–≥–Ľ.) . 22 (2): 169‚ÄĒ191. Bibcode :1963AnPhy..22..169R . doi :10.1016/0003-4916(63)90051-4 . ‚ÜĎ Stephen Lyle (2008). Uniformly Accelerating Charged Particles: A Threat to the Equivalence Principle (–į–Ĺ–≥–Ľ.) . Springer. ISBN 978-3540684770 ‚ÜĎ √ėyvind Gr√łn (2012). Review Article: Electrodynamics of Radiating Charges . Advances in Mathematical Physics (–į–Ĺ–≥–Ľ.) . 2012 : 528631. doi :10.1155/2012/528631 ‚ÜĎ Galeriu, C«élin (2019) "Electric charge in hyperbolic motion: the special conformal solution", European Journal of Physics 40(6) doi :10.1088/1361-6404/ab3df6
‚ÜĎ –į –Ī Kastrup, H. A. (2008). On the advancements of conformal transformations and their associated symmetries in geometry and theoretical physics. Annalen der Physik (–į–Ĺ–≥–Ľ.) . 520 (9‚Äď10): 631‚ÄĒ690. arXiv :0808.2730 Bibcode :2008AnP...520..631K . doi :10.1002/andp.200810324 . ‚ÜĎ –į –Ī Fulton, T., Rohrlich, F., & Witten, L. (1962). Physical consequences of a co-ordinate transformation to a uniformly accelerating frame. Il Nuovo Cimento (–į–Ĺ–≥–Ľ.) . 26 (4): 652‚ÄĒ671. Bibcode :1962NCim...26..652F . doi :10.1007/BF02781794 .
Leigh Page (Feb 1936). A New Relativity. Paper I. Fundamental Principles and Transformations Between Accelerated Systems. Physical Review 49 (3): 254‚ÄĒ268. Bibcode :1936PhRv...49..254P . doi :10.1103/PhysRev.49.254 .Leigh Page & Norman I. Adams (Mar 1936). A New Relativity. Paper II. Transformation of the Electromagnetic Field Between Accelerated Systems and the Force Equation. Physical Review . 49 (6): 466‚ÄĒ469. Bibcode :1936PhRv...49..466P . doi :10.1103/PhysRev.49.466 . Misner, Charles W. ; Thorne, Kip. S. ; Wheeler, John A. (1973), Gravitation , W. H. Freeman, Chapter 6, ISBN 0-7167-0344-0 Rindler Wolfgang (1960). Hyperbolic Motion in Curved Space Time. Physical Review 119 (6): 2082‚ÄĒ2089. Bibcode :1960PhRv..119.2082R . doi :10.1103/PhysRev.119.2082 . Ludwik Silberstein [en] The Theory of Relativity Naber, Gregory L., The Geometry of Minkowski Spacetime , Springer-Verlag, New York, 1992. ISBN 0-387-97848-8 (hardcover), ISBN 0-486-43235-1 (Dover paperback edition). pp 58‚Äď60.

















![{\displaystyle {\scriptstyle {\begin{array}{c|c}{\begin{aligned}u(T)&={\frac {u_{0}\gamma _{0}+\alpha T}{\sqrt {1+\left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)^{2}}}}\quad \\&=c\tanh \left\{\operatorname {arsinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)\right\}\\X(T)&=X_{0}+{\frac {c^{2}}{\alpha }}\left({\sqrt {1+\left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)^{2}}}-\gamma _{0}\right)\\&=X_{0}+{\frac {c^{2}}{\alpha }}\left\{\cosh \left[\operatorname {arsinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)\right]-\gamma _{0}\right\}\\c\tau (T)&=c\tau _{0}+{\frac {c^{2}}{\alpha }}\ln \left({\frac {{\sqrt {c^{2}+\left(u_{0}\gamma _{0}+\alpha T\right){}^{2}}}+u_{0}\gamma _{0}+\alpha T}{\left(c+u_{0}\right)\gamma _{0}}}\right)\\&=c\tau _{0}+{\frac {c^{2}}{\alpha }}\left\{\operatorname {arsinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)-\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)\right\}\end{aligned}}&{\begin{aligned}u(\tau )&=c\tanh \left\{\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right\}\\\\X(\tau )&=X_{0}+{\frac {c^{2}}{\alpha }}\left\{\cosh \left[\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right]-\gamma _{0}\right\}\\\\cT(\tau )&=cT_{0}+{\frac {c^{2}}{\alpha }}\left\{\sinh \left[\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right]-{\frac {u_{0}\gamma _{0}}{c}}\right\}\end{aligned}}\end{array}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06b3bf81e2e1800bf5f97de52e2bc322b2f2ae18)







































