 Геометричне представлення різних математичних середніх. a, b - два числа. A = арифметичне середнє чисел 'a' і 'b'. G = геометричне середнє, H = гармонійне середнє, Q = середнє квадратичне Геометричне представлення різних математичних середніх. a, b - два числа. A = арифметичне середнє чисел 'a' і 'b'. G = геометричне середнє, H = гармонійне середнє, Q = середнє квадратичне
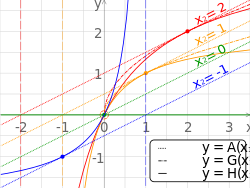 Порівняння арифметичних, геометричних і гармонійних середніх пар чисел. Вертикальні пунктирні лінії є асимптотами для гармонійних. Порівняння арифметичних, геометричних і гармонійних середніх пар чисел. Вертикальні пунктирні лінії є асимптотами для гармонійних.
У математиці три класичні засоби Піфагорових середніх: середнє арифметичне (AM), середнє геометричне (GM) і середнє гармонійне (HM). Ці засоби були пропорційно вивчені піфагорійцями разом з пізнішим поколінням грецьких математиків[1], через їхню важливість у геометрії та музиці.
Визначення
Вони визначаються так:
![{\displaystyle {\begin{aligned}\operatorname {AM} \left(x_{1},\;\ldots ,\;x_{n}\right)&={\frac {1}{n}}\left(x_{1}+\;\cdots \;+x_{n}\right)\\[9pt]\operatorname {GM} \left(x_{1},\;\ldots ,\;x_{n}\right)&={\sqrt[{n}]{\left\vert x_{1}\times \,\cdots \,\times x_{n}\right\vert }}\\[9pt]\operatorname {HM} \left(x_{1},\;\ldots ,\;x_{n}\right)&={\frac {n}{\displaystyle {\frac {1}{x_{1}}}+\;\cdots \;+{\frac {1}{x_{n}}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bbc1d421516030837da58eb09d16d4c9a93a6f3)
Властивості
Кожне значення  має наступні властивості: має наступні властивості:
- Збереження цінності
 - Однорідна функція першої послідовності
 - Інваріантність при перестановці
 - для будь-якої
 та та  . .
- Виведення середньої величини

Гармонійні і арифметичні середні є взаємними двійниками один одного для позитивних аргументів:

в той час як середнє геометричне — це його власна взаємна подвійність:

Нерівності серед середніх
Існує впорядкування цих середніх (якщо всі  позитивні) позитивні)

з рівноправністю, тільки якщо всі  рівні. рівні.
Це узагальнення нерівності арифметичних і геометричних середніх і окремий випадок нерівності для середнього степеневого. Доказ випливає з арифметико-геометричної середньої нерівності,  та взаємної подвійності ( та взаємної подвійності ( і і  також взаємні подвійні). також взаємні подвійні).
Вивчення піфагорових середніх тісно пов'язане з вивченням мажоризації й шур-опуклої функції[en]. Гармонійними і геометричними середніми є увігнуті симетричні функції їхніх аргументів.
Примітки
- ↑ Heath, Thomas. History of Ancient Greek Mathematics.
Посилання
|
|---|
| Середнє | |
|---|
| Геометрія | |
|---|
Теорія ймовірностей
та мат. статистика | |
|---|
| Теореми | |
|---|
| Нерівності | |
|---|
|


![{\displaystyle {\begin{aligned}\operatorname {AM} \left(x_{1},\;\ldots ,\;x_{n}\right)&={\frac {1}{n}}\left(x_{1}+\;\cdots \;+x_{n}\right)\\[9pt]\operatorname {GM} \left(x_{1},\;\ldots ,\;x_{n}\right)&={\sqrt[{n}]{\left\vert x_{1}\times \,\cdots \,\times x_{n}\right\vert }}\\[9pt]\operatorname {HM} \left(x_{1},\;\ldots ,\;x_{n}\right)&={\frac {n}{\displaystyle {\frac {1}{x_{1}}}+\;\cdots \;+{\frac {1}{x_{n}}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bbc1d421516030837da58eb09d16d4c9a93a6f3)



























