Тестові функції для оптимізації
У прикладній математиці тестові функції для оптимізації (штучні ландшафти) — нелінійні функції, які використовують для оцінки характеристик алгоритмів оптимізації, таких як: швидкість збіжності; точність; грубість; загальні характеристики.
Нижче наведені деякі функції тестування оптимізаційних алгоритмів, що дозволяють отримати уявлення про різні характерні ситуації, з якими стикаються алгоритми оптимізації при вирішенні задач такого роду. У першій частині наведені функції для тестування алгоритмів пошуку глобального мінімуму (максимуму). У другій частині функції з відповідними фронтами для алгоритмів багатокритеріальної оптимізації.
Штучні ландшафти, наведені для тестування оптимізаційних алгоритмів, взяті з декількох джерел (див. Посилання).
Загальний вигляд рівняння, графік цільової функції, межі змінних об'єкта і координати глобального мінімуму наведені в таблиці.
Функції для алгоритмів пошуку глобального мінімуму
| Назва / Рисунок |
Формула |
Мінімум |
Область пошуку
|
Ackley's function 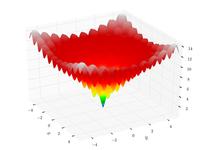
|


|

|

|
Sphere function 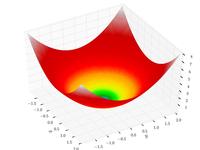
|

|

|
 , , 
|
Функція Розенброка 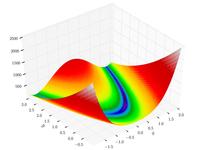
|
![{\displaystyle f({\boldsymbol {x}})=\sum _{i=1}^{n-1}\left[100\left(x_{i+1}-x_{i}^{2}\right)^{2}+\left(x_{i}-1\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ac655db50e19ee2f79a97196565e8773cd7d659)
|

|
 , , 
|
Beale's function 
|


|

|

|
Goldstein–Price function 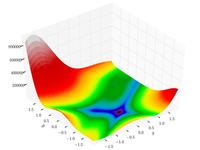
|



|

|

|
Booth's function 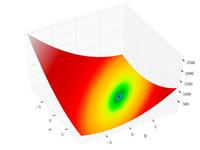
|

|

|

|
Bukin function N.6 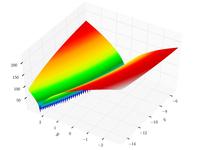
|

|

|
 , , 
|
Matyas function 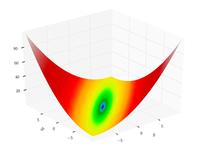
|

|

|

|
Lévi function N.13 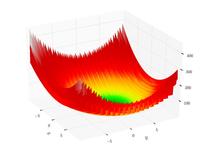
|


|

|

|
Three-hump camel function 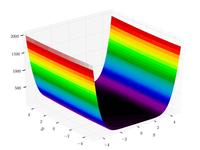
|

|

|

|
Easom function 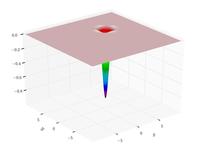
|


|

|

|
Cross-in-tray function 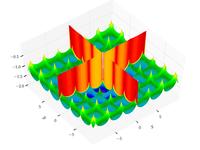
|


|

|

|
Eggholder function 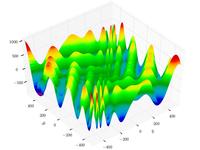
|


|

|

|
Hölder table function 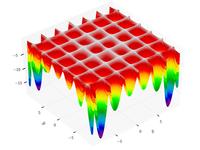
|

|

|

|
McCormick function 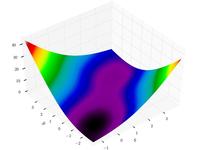
|

|

|
 , , 
|
Schaffer function N. 2 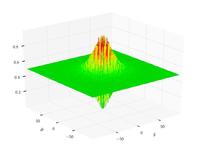
|

|

|

|
Schaffer function N. 4 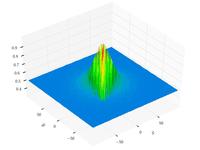
|

|

|

|
Styblinski–Tang function 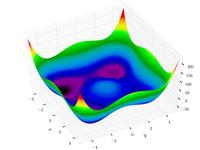
|

|


|
 , ,  . .
|
Simionescu function[1] 
|
 , ,


|

|

|
Функції для алгоритмів багатокритеріальної оптимізації
| Назва / Рисунок |
Формула |
Мінімум |
Область пошуку
|
Binh and Korn function 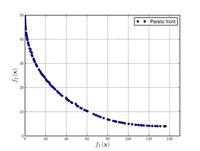
|

|

|
 , , 
|
Chakong and Haimes function 
|

|

|

|
Fonseca and Fleming function 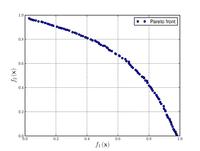
|

|
|
 , , 
|
Test function 4 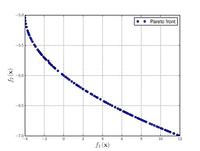
|

|

|

|
Kursawe function 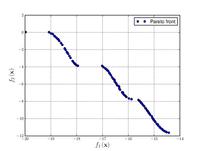
|
![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=\sum _{i=1}^{2}\left[-10\exp \left(-0.2{\sqrt {x_{i}^{2}+x_{i+1}^{2}}}\right)\right]\\&\\f_{2}\left({\boldsymbol {x}}\right)&=\sum _{i=1}^{3}\left[\left|x_{i}\right|^{0.8}+5\sin \left(x_{i}^{3}\right)\right]\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a545df8c08a178973284eae8924aab67ce46077a)
|
|
 , ,  . .
|
Schaffer function N. 1 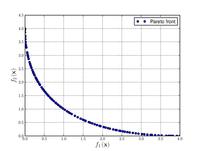
|

|
|
 . Values of . Values of  form form  to to  have been used successfully. Higher values of have been used successfully. Higher values of  increase the difficulty of the problem. increase the difficulty of the problem.
|
Schaffer function N. 2 
|

|
|
 . .
|
Poloni's two objective function 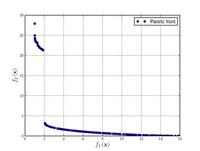
|
![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)&=\left[1+\left(A_{1}-B_{1}\left(x,y\right)\right)^{2}+\left(A_{2}-B_{2}\left(x,y\right)\right)^{2}\right]\\f_{2}\left(x,y\right)&=\left(x+3\right)^{2}+\left(y+1\right)^{2}\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6b4a1275cbe615b285fbbcdb840a9a488360cc5)

|
|

|
Zitzler–Deb–Thiele's function N. 1 
|

|
|
 , ,  . .
|
Zitzler–Deb–Thiele's function N. 2 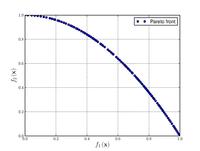
|

|
|
 , ,  . .
|
Zitzler–Deb–Thiele's function N. 3 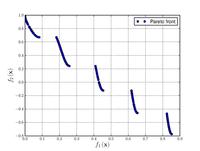
|

|
|
 , ,  . .
|
Zitzler–Deb–Thiele's function N. 4 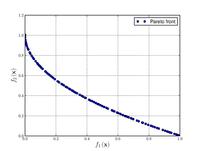
|

|
|
 , ,  , , 
|
Zitzler–Deb–Thiele's function N. 6 
|
![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=1-\exp \left(-4x_{1}\right)\sin ^{6}\left(6\pi x_{1}\right)\\f_{2}\left({\boldsymbol {x}}\right)&=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)&=1+9\left[{\frac {\sum _{i=2}^{10}x_{i}}{9}}\right]^{0.25}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)&=1-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)^{2}\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73a519e6f7ca429b41031cd0873fce161941b009)
|
|
 , ,  . .
|
Viennet function 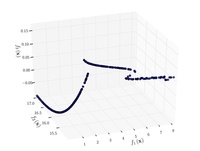
|

|
|
 . .
|
Osyczka and Kundu function 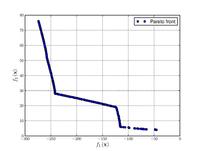
|



|

|
 , ,  , ,  . .
|
CTP1 function (2 variables) 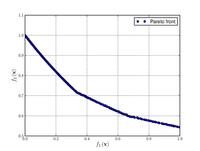
|

|

|
 . .
|
Constr-Ex problem 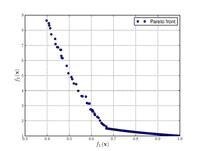
|

|

|
 , , 
|
Примітки
- ↑ Simionescu, P.A. (2014). Computer Aided Graphing and Simulation Tools for AutoCAD Users (вид. 1st). Boca Raton, FL: CRC Press. ISBN 9-781-48225290-3.
Посилання
Джерела
- Bäck, Thomas. Evolutionary algorithms in theory and practice: evolution strategies, evolutionary programming, genetic algorithms. Oxford: Oxford University Press. — 1995. p. 328. ISBN 0-19-509971-0.
- Deb, Kalyanmoy (2002) Multiobjective optimization using evolutionary algorithms (Repr. ed.). Chichester [u.a.]: Wiley. ISBN 0-471-87339-X.
- Binh T. and Korn U. MOBES: A Multiobjective Evolution Strategy for Constrained Optimization Problems. In: Proceedings of the Third International Conference on Genetic Algorithms. Czech Republic. — 1997. pp. 176—182
- Binh T. A multiobjective evolutionary algorithm. The study cases. Technical report. Institute for Automation and Communication. Barleben, Germany. — 1999.
|











![{\displaystyle f({\boldsymbol {x}})=\sum _{i=1}^{n-1}\left[100\left(x_{i+1}-x_{i}^{2}\right)^{2}+\left(x_{i}-1\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ac655db50e19ee2f79a97196565e8773cd7d659)




















































































![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=\sum _{i=1}^{2}\left[-10\exp \left(-0.2{\sqrt {x_{i}^{2}+x_{i+1}^{2}}}\right)\right]\\&\\f_{2}\left({\boldsymbol {x}}\right)&=\sum _{i=1}^{3}\left[\left|x_{i}\right|^{0.8}+5\sin \left(x_{i}^{3}\right)\right]\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a545df8c08a178973284eae8924aab67ce46077a)











![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)&=\left[1+\left(A_{1}-B_{1}\left(x,y\right)\right)^{2}+\left(A_{2}-B_{2}\left(x,y\right)\right)^{2}\right]\\f_{2}\left(x,y\right)&=\left(x+3\right)^{2}+\left(y+1\right)^{2}\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6b4a1275cbe615b285fbbcdb840a9a488360cc5)















![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=1-\exp \left(-4x_{1}\right)\sin ^{6}\left(6\pi x_{1}\right)\\f_{2}\left({\boldsymbol {x}}\right)&=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)&=1+9\left[{\frac {\sum _{i=2}^{10}x_{i}}{9}}\right]^{0.25}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)&=1-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)^{2}\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73a519e6f7ca429b41031cd0873fce161941b009)


































