дәӨдә’ејҸиҜҒжҳҺзі»з»ҹ
еңЁи®Ўз®—еӨҚжқӮжҖ§зҗҶи®әдёӯпјҢдәӨдә’ејҸиҜҒжҳҺдҪ“зі»пјҲд»ҘдёӢз®Җз§°дәӨдә’иҜҒжҳҺпјүжҳҜдёҖзұ»и®Ўз®—жЁЎеһӢгҖӮеғҸе…¶е®ғи®Ўз®—жЁЎеһӢдёҖж ·пјҢдәӨдә’иҜҒжҳҺзҡ„зӣ®ж ҮжҳҜпјҡеҜ№дёҖдёӘиҜӯиЁҖLпјҢе’ҢдёҖдёӘз»ҷе®ҡзҡ„иҫ“е…ҘxпјҢеҲӨж–ӯxжҳҜеҗҰеңЁLдёӯгҖӮдәӨдә’иҜҒжҳҺз”ұдёӨдёӘе®һдҪ“пјҡйӘҢиҜҒиҖ…пјҲverifierпјүе’ҢиҜҒжҳҺиҖ…пјҲproverпјүз»„жҲҗпјҢдёӨиҖ…йғҪеҸҜд»ҘзңӢдҪңжҳҜжҹҗзұ»еӣҫзҒөжңәгҖӮиҖҢе®ғзҡ„и®Ўз®—иҝҮзЁӢдёәпјҡз»ҷе®ҡдәҶиҫ“е…ҘxпјҢйҖҡиҝҮйӘҢиҜҒиҖ…е’ҢиҜҒжҳҺиҖ…д№Ӣй—ҙдәӨжҚўдҝЎжҒҜпјҢжңҖз»ҲпјҢз”ұйӘҢиҜҒиҖ…жқҘж №жҚ®иҜҒжҳҺиҖ…з»ҷеҮәзҡ„дҝЎжҒҜпјҢеҲӨж–ӯз»ҷе®ҡзҡ„иҫ“е…ҘжҳҜдёҚжҳҜеңЁиҜӯиЁҖLдёӯгҖӮ дәӨдә’иҜҒжҳҺзҡ„еҹәжң¬еҒҮи®ҫжҳҜпјҡиҜҒжҳҺиҖ…еңЁи®Ўз®—иғҪеҠӣдёҠжҳҜж— йҷҗзҡ„пјҢеңЁжҰӮзҺҮеӨҡйЎ№ејҸж—¶й—ҙпјҲBPP (иӨҮйӣңеәҰ)пјүзҡ„еӣҫзҒөжңәгҖӮдёҖиҲ¬жқҘиҜҙпјҢеҜ№з»ҷе®ҡзҡ„LпјҢжҲ‘们关注зҡ„жҳҜдәӨдә’иҜҒжҳҺдёӯйӘҢиҜҒиҖ…VиҝҷдёҖи§’иүІпјҢ并еҜ№е®ғеҠ д»ҘеҰӮдёӢзҡ„иҰҒжұӮпјҡ
еҰӮжһңеҜ№LпјҢиҝҷж ·зҡ„йӘҢиҜҒиҖ…еӯҳеңЁпјҢйӮЈд№Ҳз§°Lжңүиҝҷж ·зҡ„дёҖдёӘдәӨдә’дҪ“зі»гҖӮ зұ»дјјеҜ№еӣҫзҒөжңәжүҖйңҖзҡ„иҝҗиЎҢж—¶й—ҙе’Ңз©әй—ҙзӯүеҠ д»ҘйҷҗеҲ¶жқҘеҫ—еҲ°иҜӯиЁҖзҡ„йӣҶеҗҲвҖ”вҖ”еӨҚжқӮжҖ§зұ»дёҖж ·пјҢйҖҡиҝҮж”№еҸҳдәӨдә’иҜҒжҳҺдёӯпјҢдәӨдә’иҝҮзЁӢзҡ„иҪ®ж•°гҖҒйҡҸжңәжәҗжҳҜе…¬ејҖзҡ„иҝҳжҳҜйӘҢиҜҒиҖ…жүҖз§Ғжңүзҡ„пјҢд»ҘеҸҠиҜҒжҳҺиҖ…зҡ„ж•°зӣ®зӯүзӯүеҸӮж•°пјҢеҸҜд»Ҙеҫ—еҲ°дёҚеҗҢиғҪеҠӣзҡ„иҜҒжҳҺдҪ“зі»пјҢ并дҫқжҚ®дёҖдёӘиҜӯиЁҖжҳҜдёҚжҳҜжңүиҝҷж ·еҸӮж•°зҡ„дәӨдә’иҜҒжҳҺпјҢжқҘе®ҡд№үзӣёеә”зҡ„иҜӯиЁҖзҡ„йӣҶеҗҲвҖ”вҖ”еӨҚжқӮжҖ§зұ»гҖӮдҫқжҚ®дәӨдә’иҜҒжҳҺе®ҡд№үзҡ„дё»иҰҒеӨҚжқӮжҖ§зұ»жңүIPе’ҢAMпјҢе®ғ们дёҺдҫқжҚ®еӣҫзҒөжңәе®ҡд№үзҡ„з»Ҹе…ёеӨҚжқӮжҖ§зұ»зҡ„е…ізі»жҳҜйҮҚиҰҒзҡ„з ”з©¶иҜҫйўҳгҖӮ NPеҜјиҮҙдәӨдә’иҜҒжҳҺзҡ„еҸ‘зҺ°зҡ„第дёҖдёӘи§ӮеҜҹжҳҜеҜ№NPзҡ„еҰӮдёӢзҡ„зҗҶи§ЈпјҡNPеҸҜд»ҘзҗҶи§Јдёәи§ЈеҸҜд»ҘеңЁеӨҡйЎ№ејҸж—¶й—ҙиҝӣиЎҢйӘҢиҜҒзҡ„й—®йўҳзҡ„йӣҶеҗҲпјҢиҖҢжұӮиҝҷдёӘи§Јзҡ„иҝҮзЁӢеҸҜиғҪжҳҜиҫғдёәеӣ°йҡҫзҡ„пјҢеҰӮеҜ№NPе®ҢеӨҮй—®йўҳпјҢзҺ°д»Ҡд»ҚжңӘжңүеӨҡйЎ№ејҸж—¶й—ҙзҡ„з®—жі•гҖӮиҝҷж ·пјҢвҖңйӘҢиҜҒи§ЈвҖқе’ҢвҖңжұӮи§ЈвҖқиҝҷдёӨйЎ№и®Ўз®—д»»еҠЎе°ұжңүдәҶи®Ўз®—иғҪеҠӣдёҠзҡ„е·®ејӮгҖӮжүҖд»ҘеҸҜд»ҘеҒҮи®ҫвҖңйӘҢиҜҒи§ЈвҖқжҳҜз”ұйӘҢиҜҒиҖ…е®ҢжҲҗпјҲеңЁNPзҡ„жғ…еҶөдёӢпјҢжҳҜзЎ®е®ҡжҖ§еӨҡйЎ№ејҸж—¶й—ҙеӣҫзҒөжңәпјүпјҢиҖҢвҖңжұӮи§ЈвҖқжҳҜз”ұдёҖдёӘиғҪеҠӣжӣҙејәзҡ„еӣҫзҒөжңәе®ҢжҲҗзҡ„пјҲеңЁNPзҡ„жғ…еҶөдёӢпјҢеҸҜд»ҘеҒҮи®ҫжҳҜзЎ®е®ҡжҖ§жҢҮж•°ж—¶й—ҙеӣҫзҒөжңәпјүгҖӮдёӢйқўз”ЁPTMд»ЈиЎЁзЎ®е®ҡжҖ§еӨҡйЎ№ејҸж—¶й—ҙеӣҫзҒөжңәгҖӮ дәҺжҳҜд»ҺNPпјҢеҸҜд»Ҙи®ҫи®ЎеҰӮдёӢзҡ„дәӨдә’иҜҒжҳҺпјҡз»ҷе®ҡLвҲҲNPпјҢе’ҢxвҲҲLпјҢжҲ‘们зҹҘйҒ“еҜ№xзҡ„дёҖдёӘи§ЈwпјҢжңүдёҖPTMпјҢеҜ№иҫ“е…Ҙ(x, w)пјҢиҫ“еҮәвҖңжҺҘеҸ—вҖқеҪ“дё”д»…еҪ“wжҳҜxзҡ„дёҖдёӘи§ЈгҖӮиҖғиҷ‘дёҖиҪ®зҡ„пјҢз”ұиҜҒжҳҺиҖ…PеҸ‘иө·зҡ„дәӨдә’иҜҒжҳҺпјҡ
еӣ жӯӨпјҢNPжҳҜеҢ…еҗ«еңЁиҪ®ж•°дёә1гҖҒдәӨжҚўдҝЎжҒҜй•ҝеәҰдёәеӨҡйЎ№ејҸзҡ„гҖҒйӘҢиҜҒиҖ…жҳҜзЎ®е®ҡжҖ§еӣҫзҒөжңәзҡ„иҜҒжҳҺдҪ“зі»дёӯзҡ„гҖӮеҸҚиҝҮжқҘпјҢиҝҷж ·зҡ„иҜҒжҳҺдҪ“зі»е®ҡд№үзҡ„иҜӯиЁҖе®№жҳ“зңӢеҮәд№ҹжҳҜеңЁNPдёӯзҡ„гҖӮиҝҷж ·NPе°ұдёҺиҝҷж ·зҡ„иҜҒжҳҺдҪ“зі»зӯүд»·гҖӮеҸҜд»ҘиҜҒжҳҺпјҢеҪ“йӘҢиҜҒиҖ…жҳҜзЎ®е®ҡжҖ§еӣҫзҒөжңәпјҢжҜҸиҪ®дәӨжҚўдҝЎжҒҜй•ҝеәҰдёәеӨҡйЎ№ејҸзҡ„пјҢеҚідҫҝе°ҶиҪ®ж•°жү©еұ•жҲҗеӨҡйЎ№ејҸиҪ®пјҢжүҖеҫ—еҲ°зҡ„дәӨдә’иҜҒжҳҺд»Қ然дёҺNPжҳҜзӯүд»·зҡ„гҖӮиҝҷж ·е°ұйңҖиҰҒе°ҶйӘҢиҜҒиҖ…жү©еұ•жҲҗйҡҸжңәжҖ§еӣҫзҒөжңәпјҢжӯӨж—¶е°ұжңүдәҶдёӢйқўзҡ„жңүи¶Јзҡ„еӨҚжқӮжҖ§зұ»гҖӮ жў…жһ—-дәҡз‘ҹеҚҸи®®пјҲMAпјүдҝқжҢҒиҪ®ж•°дёә1иҪ®пјҢз”ұиҜҒжҳҺиҖ…еҸ‘иө·пјҢиҖҢе°ҶдёҠйқўзҡ„PTMжҚўдҪңжҰӮзҺҮеӨҡйЎ№ејҸж—¶й—ҙеӣҫзҒөжңәпјҢеҸҜд»Ҙеҫ—еҲ°еӨҚжқӮжҖ§зұ»MA:йӘҢиҜҒиҖ…жҳҜдёҖдёӘеңЁжҰӮзҺҮеӨҡйЎ№ејҸж—¶й—ҙзҡ„еӣҫзҒөжңә(дәҡз‘ҹ)пјҢиҜҒжҳҺиҖ…пјҲжў…жһ—пјүз»ҷеҮәеҜ№дәҺй—®йўҳзҡ„и§Јд№ӢеҗҺйӘҢиҜҒиҖ…еҝ…йЎ»еңЁ1/3зҡ„й”ҷиҜҜзҺҮд»ҘеҶ…еҶіе®ҡnжҳҜеҗҰеңЁиҝҷдёӘиҜӯиЁҖд№ӢеҶ…гҖӮ жӣҙжӯЈејҸең°иҜҙпјҡ еҜ№д»»дҪ•иҜӯиЁҖL, иӢҘжҳҜеӨҡйЎ№ејҸ:
The second condition can alternatively be written as
дәҡз‘ҹ-жў…жһ—еҚҸи®®пјҲAMпјү
IPеңЁи®Ўз®—еӨҚжқӮжҖ§зҗҶи®әеҶ…пјҢIPжҳҜз”ұд»ҘдёӢзү№е®ҡдәӨдә’ејҸиҜҒжҳҺзі»з»ҹжүҖиғҪи§ЈеҶізҡ„дёҖзұ»й—®йўҳпјҡйӘҢиҜҒиҖ…жҳҜдёҖдёӘеңЁжҰӮзҺҮеӨҡйЎ№ејҸж—¶й—ҙзҡ„еӣҫзҒөжңәпјҢеҸҢж–№еҸҜд»ҘдәӨжҚўеӨҡйЎ№ејҸж¬ЎдҝЎжҒҜпјҢжңҖеҗҺйӘҢиҜҒиҖ…еҝ…йЎ»еңЁ1/3зҡ„й”ҷиҜҜзҺҮд»ҘеҶ…еҶіе®ҡnжҳҜеҗҰеңЁиҝҷдёӘиҜӯиЁҖд№ӢеҶ…гҖӮпјҲжүҖд»ҘеңЁBPPеҶ…зҡ„иҜӯиЁҖдёҖе®ҡеңЁIPд№ӢеҶ…пјҢеӣ дёәжҲ‘们еҸҜд»Ҙи®©йӘҢиҜҒиҖ…зӣҙжҺҘеҝҪз•ҘиҜҒжҳҺиҖ…然еҗҺиҮӘе·ұеҜ№иҝҷй—®йўҳдҪңеҶіе®ҡгҖӮпјү жӣҙжӯЈејҸзҡ„иҜҙпјҡ еҜ№д»»дҪ•иҜӯиЁҖL, иӢҘ:
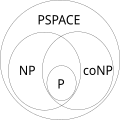
е’ҢAMдёҚеҗҢд№ӢеӨ„еңЁдәҺпјҢе®ғзҡ„дәӨжҚўдҝЎжҒҜж¬Ўж•°жҳҜиў«еёёж•°ж¬Ўж•°иҖҢйқһиў«дёҖдёӘеӨҡйЎ№ејҸж¬Ўж•°жүҖйҷҗе®ҡгҖӮ IP = PSPACEиҰҒиҜҒжҳҺIPдёҺPSPACEзӣёзӯүпјҢжҲ‘们е…ҲиҜҒжҳҺеҮәIPжҳҜPSPACEзҡ„еӯҗйӣҶпјҢ然еҗҺиҜҒжҳҺPSPACEд№ҹжҳҜIPзҡ„еӯҗйӣҶпјҢеӣ жӯӨд№Ӣж•…дёӨдёӘйӣҶеҗҲзӣёзӯүгҖӮиҰҒиҜҒжҳҺеҮәпјҢжҲ‘们еұ•зҺ°еҮәдёҖдёӘз”ЁеӨҡйЎ№ејҸз©әй—ҙзҡ„жңәеҷЁеҸҜд»ҘжҖҺж ·жЁЎжӢҹдёҖдёӘдәӨдә’ејҸиҜҒжҳҺзі»з»ҹгҖӮиҰҒиҜҒжҳҺиҝҷдёҖ件дәӢпјҢжҲ‘们жҺЁеҜјдёҖдёӘPSPACE-е®Ңе…ЁиҜӯиЁҖTQBFжҳҜеңЁIPйҮҢйқўгҖӮиҝҷдёӨдёӘйғЁд»Ҫзҡ„иҜҒжҳҺеқҮжҳҜз”ұSipserжҸҗеҮәзҡ„гҖӮ
и®ҫAжҳҜIPйҮҢзҡ„дёҖдёӘиҜӯиЁҖгҖӮ Now, assume that on input w with length n, A'зҡ„жЈҖйӘҢиҖ…V exchanges exactly messages.жҲ‘们зҺ°еңЁе»әз«ӢдёҖдёӘжңәеҷЁMжқҘжЁЎжӢҹVпјҢ并且MжҳҜPSPACEжңәеҷЁгҖӮ дёәдәҶиҫҫеҲ°иҝҷдёӘзӣ®зҡ„пјҢжҲ‘们е®ҡд№үMеҰӮдёӢпјҡ ж №жҚ®зҡ„е®ҡд№ү, we have if and if . зҺ°еңЁпјҢжҲ‘们еҸҜд»Ҙе®ҡд№үпјҡ 并且еҜ№д»»дҪ• and every message history пјҢжҲ‘们еҪ’зәіе®ҡд№үиҝҷдёӘеҮҪж•°еҰӮдёӢпјҡ where the term is defined as follows:
дёәдәҶеұ•зӨәжҲ‘们иҜҒжҳҺзҡ„ж–№жі•пјҢжҲ‘们е…ҲиҜҒжҳҺдёҖдёӘжҜ”иҫғејұзҡ„зҗҶи®әпјҡпјҲжңҖж—©з”ұLund, et al.иҜҒжҳҺпјүгҖӮ然еҗҺеҲ©з”ЁиҝҷдёӘиҜҒжҳҺзҡ„жҰӮеҝөеҺ»иҜҒжҳҺгҖӮ既然TQBF PSPACE-е®Ңе…ЁпјҢжҲ‘们еҸҜд»Ҙеҫ—зҹҘиӢҘеҲҷPSPACE IPпјҢеӣ жӯӨиҜҒжҳҺPSPACE IP.
жҲ‘们ејҖе§ӢиҜҒжҳҺеҰӮдёӢпјҡ
MIPеңЁ1988е№ҙпјҢGoldwasser et al.еҹәдәҺIPеҲӣйҖ дәҶеҸҰдёҖдёӘжӣҙејәзҡ„дәӨдә’ејҸиҜҒжҳҺзі»з»ҹMIPпјҢе®ғеҢ…еҗ«дёӨдёӘзӢ¬з«Ӣзҡ„иҜҒжҳҺиҖ…гҖӮдёҖж—ҰжЈҖйӘҢиҖ…ејҖе§Ӣи·ҹиҜҒжҳҺиҖ…жІҹйҖҡзҡ„ж—¶еҖҷпјҢиҝҷдёӨдҪҚиҜҒжҳҺиҖ…е°ұдёҚиғҪдә’зӣёжІҹйҖҡгҖӮеӨҡдәҶдёҖдёӘиҜҒжҳҺиҖ…и®©жЈҖйӘҢиҖ…еҸҜд»ҘжЈҖжҹҘ第дёҖдёӘиҜҒжҳҺиҖ…зҡ„иҜҒжҳҺпјҢдјҡи®©йҒҝе…ҚжЈҖйӘҢиҖ…иў«иҜҒжҳҺиҖ…ж¬әйӘ—зҡ„е·ҘдҪңеҸҳеҫ—жӣҙз®ҖеҚ•пјҢе°ұеғҸзҠҜдәәиҮӘзҷҪж—¶и®©д»–дёҺд»–зҡ„еҗҢдјҷеҲҶејҖеңЁдёӨдёӘж— жі•дә’зӣёжІҹйҖҡзҡ„ең°ж–№иҮӘзҷҪж—¶дјҡжҜ”иҫғе®№жҳ“жүҫеҮә他们жҳҜеҗҰиҜҙи°ҺдёҖж ·гҖӮдәӢе®һдёҠпјҢиҝҷдёҖ件дәӢзҡ„е·®ејӮеӨ§еҲ°Babai, FortnowпјҢе’ҢLundиҜҒжҳҺдәҶMIP = NEXPTIMEпјҢиҝҷзұ»й—®йўҳжҳҜеңЁжҢҮж•°ж—¶й—ҙд№ӢеҶ…д»ҘйқһеҶіе®ҡжҖ§и§Јзҡ„еҮәжқҘзҡ„й—®йўҳпјҢиҝҷжҳҜдёҖдёӘйқһеёёеӨ§зҡ„зұ»еҲ«гҖӮжӯӨеӨ–пјҢеңЁMIPзі»з»ҹеҶ…пјҢеҚідҪҝдёҚеҒҡд»»дҪ•еӨҡдҪҷзҡ„еҒҮи®ҫпјҢжүҖжңүзҡ„NPиҜӯиЁҖеқҮжңүйӣ¶зҹҘиҜҶиҜҒжҳҺпјӣеңЁIPйҮҢйқўе”ҜжңүеҒҮи®ҫеӯҳеңЁеҚ•еҗ‘еҮҪејҸжүҚеҸҜиғҪжҲҗз«ӢгҖӮ IPPIPPпјҲunbounded IPпјүжҳҜ IPзҡ„дёҖз§ҚеҸҳдҪ“пјҢе°ҶеҺҹжқҘзҡ„BPPжЈҖйӘҢиҖ…жҚўжҲҗPPжЈҖйӘҢиҖ…гҖӮжӣҙзІҫзЎ®зҡ„иҜҙпјҢжҲ‘们е°Ҷе®ҢеӨҮжҖ§и·ҹеҸҜйқ жҖ§зҡ„жқЎд»¶дҝ®ж”№еҰӮдёӢпјҡ
иҷҪ然IPPд»Қж—§дёҺPSPACEзӣёзӯүпјҢдҪҶжҳҜIPPеҚҸи®®зі»з»ҹеңЁж¶үеҸҠеҗҜзӨәеӣҫзҒөжңәзҡ„жғ…еҶөдёӢдёҺIPзҡ„зҠ¶еҶөе·®ејӮйўҮеӨ§пјҡеҜ№жүҖжңүзҡ„еҗҜзӨәеӣҫзҒөжңәIPP=PSPACEпјҢдҪҶжҳҜеҮ д№ҺеҜ№жүҖжңүзҡ„еҗҜзӨәеӣҫзҒөжңәпјҢIP вү PSPACEгҖӮ[1] QIPQIPжҳҜе°ҶIPзҡ„BPPжЈҖйӘҢиҖ…жҚўжҲҗдёҖдёӘBQPжЈҖйӘҢиҖ…жүҖдә§з”ҹзҡ„еҸҳдҪ“пјҢд№ҹеҚіпјҡBQPжҳҜеҸҜд»Ҙз”ЁйҮҸеӯҗи®Ўз®—жңәеңЁеӨҡйЎ№ејҸж—¶й—ҙеҶ…и§ЈеҶізҡ„й—®йўҳзұ»еҲ«гҖӮ并且пјҢиҝҷдёҖдәӣи®ҜжҒҜжҳҜз”ЁйҮҸеӯҗдҪҚжүҖиЎЁзӨәзҡ„гҖӮ[2]еңЁ2009е№ҙ, Jain, Ji, UpadhyayпјҢе’ҢWatrousиҜҒжҳҺдәҶQIPд№ҹдёҺPSPACEзӣёзӯүпјҢ[3]жҖ»з»“иө·д»ҘдёҠKitaevе’ҢWatrousзҡ„зҗҶи®әпјҢжҲ‘们еҫ—еҲ°QIPеҢ…еҗ«еңЁEXPTIMEеҶ…зҡ„з»“и®әпјҢеӣ дёәQIP = QIP[3]пјҢso that more than three rounds are never necessary.[4] compIPIPPи·ҹQIPйғҪжҳҜз»ҷдәҲжЈҖйӘҢиҖ…жӣҙеӨҡзҡ„иғҪеҠӣпјҢдҪҶжҳҜдёҖдёӘcompIPзі»з»ҹпјҲcompetitive IP proof systemпјүеҲҷжҳҜе°ҶиҜҒжҳҺиҖ…еҮҸејұеҰӮдёӢпјҡ
PCP
йӣ¶зҹҘиҜҶиҜҒжҳҺйӣ¶зҹҘиҜҶиҜҒжҳҺжҳҜдёҖз§Қзү№ж®Ҡзҡ„дәӨдә’ејҸиҜҒжҳҺпјҢе…¶дёӯиҜҒжҳҺиҖ…зҹҘйҒ“й—®йўҳзҡ„зӯ”жЎҲпјҢд»–йңҖиҰҒеҗ‘йӘҢиҜҒиҖ…иҜҒжҳҺвҖңд»–зҹҘйҒ“зӯ”жЎҲвҖқиҝҷдёҖдәӢе®һпјҢдҪҶжҳҜиҰҒжұӮйӘҢиҜҒиҖ…дёҚиғҪиҺ·еҫ—зӯ”жЎҲзҡ„д»»дҪ•дҝЎжҒҜгҖӮ еҸҜд»ҘеҸӮиҖғиҝҷж ·дёҖдёӘз®ҖеҚ•зҡ„дҫӢеӯҗгҖӮиҜҒжҳҺиҖ…е’ҢйӘҢиҜҒиҖ…йғҪжӢҝеҲ°дәҶдёҖдёӘж•°зӢ¬зҡ„йўҳзӣ®пјҢиҜҒжҳҺиҖ…зҹҘйҒ“дёҖдёӘи§Јжі•пјҢд»–еҸҜд»ҘйҮҮеҸ–еҰӮдёӢиҝҷз§Қйӣ¶зҹҘиҜҶиҜҒжҳҺж–№жі•пјҡд»–жүҫеҮә81еј зәёзүҮпјҢжҜҸдёҖеј зәёзүҮдёҠеҶҷдёҠ1еҲ°9зҡ„дёҖдёӘж•°еӯ—пјҢдҪҝеҫ—жӯЈеҘҪжңү9д»ҪеҶҷжңүд»Һ1еҲ°9зҡ„зәёзүҮгҖӮ然еҗҺеӣ дёәд»–зҹҘйҒ“зӯ”жЎҲпјҢд»–еҸҜд»ҘжҠҠжүҖжңүзҡ„зәёзүҮжҢүз…§и§Јжі•ж”ҫеңЁдёҖдёӘ9д№ҳ9зҡ„ж–№ж јеҶ…пјҢдҪҝеҫ—ж»Ўи¶іж•°зӢ¬зҡ„йўҳзӣ®иҰҒжұӮпјҲжҜҸеҲ—гҖҒжҜҸиЎҢгҖҒжҜҸдёӘд№қе®«ж јйғҪжӯЈеҘҪжңү1еҲ°9пјүгҖӮж”ҫеҘҪд№ӢеҗҺд»–жҠҠжүҖжңүзҡ„зәёзүҮзҝ»иҪ¬пјҢи®©жІЎжңүеӯ—зҡ„дёҖйқўжңқдёҠгҖӮиҝҷж ·йӘҢиҜҒиҖ…жІЎеҠһжі•зңӢеҲ°зәёзүҮдёҠзҡ„ж•°еӯ—гҖӮжҺҘдёӢжқҘпјҢйӘҢиҜҒиҖ…е°ұйӘҢиҜҒж•°зӢ¬зҡ„жқЎд»¶жҳҜеҗҰж»Ўи¶ігҖӮжҜ”еҰӮд»–йҖүдёҖеҲ—пјҢиҝҷж—¶иҜҒжҳҺиҖ…е°ұжҠҠиҝҷдёҖеҲ—зҡ„зәёзүҮ收йӣҶиө·жқҘпјҢжҠҠйЎәеәҸд»»ж„Ҹжү“д№ұпјҢ然еҗҺжҠҠзәёзүҮзҝ»иҝҮжқҘпјҢи®©йӘҢиҜҒиҖ…зңӢеҲ°1еҲ°9зҡ„зәёзүҮйғҪеҮәзҺ°дәҶгҖӮж•ҙдёӘиҝҮзЁӢдёӯйӘҢиҜҒиҖ…йғҪж— жі•еҫ—зҹҘжҜҸеј зәёзүҮзҡ„дҪҚзҪ®пјҢдҪҶжҳҜеҚҙиғҪйӘҢиҜҒзЎ®е®һжҳҜ1еҲ°9йғҪеҮәзҺ°дәҶгҖӮ зӣёй—ңжўқзӣ®еҸӮиҖғж–ҮзҢ®
|
Portal di Ensiklopedia Dunia









![{\displaystyle w\in L\Rightarrow \Pr[V\leftrightarrow P{\text{ accept }}w]\geq {\frac {2}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/980b826c63ed5c6dba58f135034c8cf64840ac8c)
![{\displaystyle w\not \in L\Rightarrow \Pr[V\leftrightarrow Q{\text{ accept }}w]\leq {\frac {1}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80fb1686a9d7b1434340ed8199ea6afa8505b041)



![{\displaystyle \Pr[V{\text{ accepts }}w]=\max _{P}\Pr[V\leftrightarrow P{\text{ accepts }}w]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8ba589fb2a58a7f0569dd7ae028c29079462b8e)

![{\displaystyle \Pr[V{\text{ accepts }}w]\geq {\frac {2}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28b7ef62ab5a8035fe8740cbd75d4952dee1ae92)

![{\displaystyle \Pr[V{\text{ accepts }}w]\leq {\frac {1}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cb0d9fed661e1fec6b81b3e78734f720c748b71)

![{\displaystyle \Pr[V{\text{ accepts }}w{\text{ starting at }}M_{j}]=\max _{P}\Pr[V\leftrightarrow P{\text{ accepts }}w{\text{ starting at }}M_{j}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b310eebf98ec01675d0d5dab3351d1eb9097d41)





![{\displaystyle {\text{wt-avg}}_{m_{j+1}}N_{M_{j+1}}=\sum _{m_{j+1}}(Pr_{r}[V(w,r,M_{j})])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f7b79c67dc3d7e68d0739569ac079fb9c5dedc0)